Problem Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.
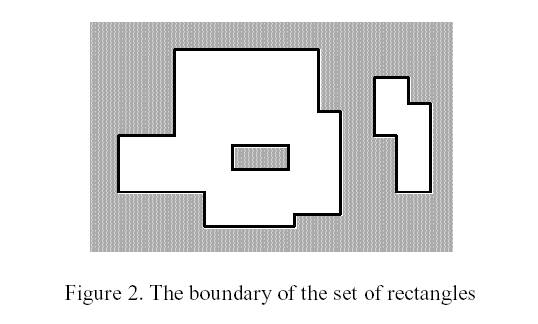
The vertices of all rectangles have integer coordinates.
Input Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
Output Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input 7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output 228
矩形周长并,同矩形面积并一样用扫面线一行行统计,竖线则记录条数。
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<cstdio>
#include<cmath>
#include<map>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int maxn = 400005;
int n, m, ans, l, r;
struct seg
{
int h, l, r;
int k;
bool operator <(const seg&a)
{
return h < a.h;
}
}p[maxn];
struct ST
{
int sum[maxn], dis[maxn], num[maxn], L[maxn], R[maxn];
void build(int x, int l, int r)
{
L[x] = R[x] = num[x] = sum[x] = dis[x] = 0;
if (l == r) return;
else
{
int mid = l + r >> 1;
build(x + x, l, mid);
build(x + x + 1, mid + 1, r);
}
}
void get(int x, int lx, int rx)
{
L[x] = L[lx]; R[x] = R[rx];
num[x] = num[lx] + num[rx];
if (R[lx] && L[rx]) num[x] -= 2;
dis[x] = dis[lx] + dis[rx];
}
void insert(int x, int l, int r, int ll, int rr, int v)
{
if (l<ll || r >rr || sum[x] + v < 0)
{
int mid = l + r >> 1;
if (sum[x])
{
insert(x + x, l, mid, l, r, sum[x]);
insert(x + x + 1, mid + 1, r, l, r, sum[x]);
sum[x] = 0;
}
if (ll <= mid) insert(x + x, l, mid, ll, rr, v);
if (rr > mid) insert(x + x + 1, mid + 1, r, ll, rr, v);
get(x, x + x, x + x + 1);
}
else
{
sum[x] += v;
if (sum[x])
{
L[x] = R[x] = 1;
num[x] = 2;
dis[x] = r - l + 1;
}
else if (l == r)
{
L[x] = R[x] = 0;
num[x] = 0;
dis[x] = 0;
}
else get(x, x + x, x + x + 1);
}
}
}st;
int main()
{
while (scanf("%d", &n) != EOF)
{
for (int i = 1; i <= n; i++)
{
scanf("%d%d%d%d", &l, &p[i + i - 1].h, &r, &p[i + i].h);
p[i + i - 1].l = p[i + i].l = l + 10001;
p[i + i - 1].r = p[i + i].r = r + 10001;
p[i + i - 1].k = -(p[i + i].k = -1);
}
sort(p + 1, p + n + n + 1);
ans = 0; st.build(1, 1, 20000);
for (int i = 1, j = st.dis[1]; i <= n + n; i++)
{
st.insert(1, 1, 20000, p[i].l, p[i].r - 1, p[i].k);
ans += abs(j - st.dis[1]) + st.num[1] * (p[i + 1].h - p[i].h);
j = st.dis[1];
}
printf("%d\n", ans);
}
return 0;
}标签:Picture,HDU,1828,int,sum,mid,num,rectangles,dis From: https://blog.51cto.com/u_15870896/5838859