概览
索引是一种数据结构,用于帮助我们在大量数据中快速定位到我们想要查找的数据。
索引好比一本好书的目录页,需要查询某个章节直接在目录页查找,然后打开响应页数。
但索引也不是就快,如果章节少,那就直接翻开书找即可很快找到,只有章节非常多时,我们就可以利用索引快速找到。
所以,如果想让索引发挥出其真正的实力,需要在数据量大之时才可放心使用索引,反之就是大材小用。
MySQL 中索引分类
- B + 树索引
- Hash 索引
- 全文索引
以下篇幅会以 InnoDB 存储引擎为例分析 B+ 树索引。
在此之前,看下 B+ 树 的演化:
graph LR A(二叉树) --> B(平衡二叉树) --> C(B 树) --> D(B+ 树)二叉树
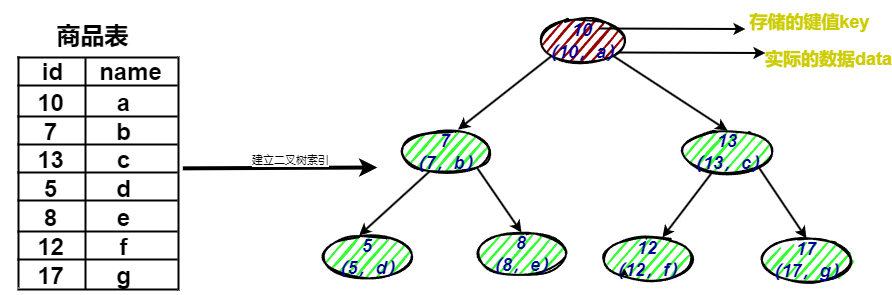
如上图中展示,商品表建立了一个二叉树查找的索引。
图中可以看到二叉树的节点,节点中存储了键(key)和数据(data);键对应商品表中的 id,数据对应商品表中的行数据。
二叉树特性:任何节点的左子节点的键值都小于当前节点的键值,右子节点的键值都大于当前节点的键值;顶端的节点为根节点,没有子节点的节点为叶子节点。
若现在要查询 id = 12 的商品信息,通过创建的二叉树索引,查询流程如下:
- 将根节点作为当前节点,把 12 与当前节点的键值 10 比较,12 大于 10,接下来把当前节点的右子节点作为当前节点,也就是 13
- 把 12 和当前节点的键值 13 比较,发现 12 小于 13,把当前节点的左子节点作为当前节点,也就是 12
- 把 12 和当前节点的键值 12 比较,12 等于 12,满足条件,从当前节点取出 data,即 id = 12,name = xm
通过二叉树查找需要 3 次即可找到匹配的数据;若在表中一条一条的查询,需要 6 次才可以找到。
平衡二叉树
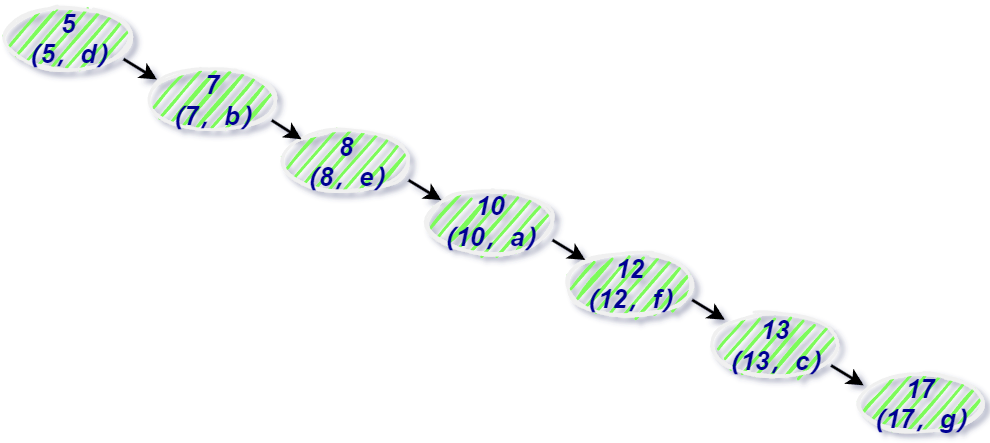
二叉树若是以上这样的结构,就变成了链表。
现在要查询 id = 17 的商品信息,需要查找 7 次,也就是相当于全表扫描;导致这样的原因主要是二叉树查找变得不平衡了,即:高度太高了,从而致使查找效率不稳定。
so,为了保证二叉树一直保持平衡,就要用到平衡二叉树呢。
平衡二叉树(AVL 树),在满足二叉查找树特性的基础上,要求每个节点的左右子树的高度差不能超过 1。如下为平衡二叉树与非平衡二叉树的比较图:
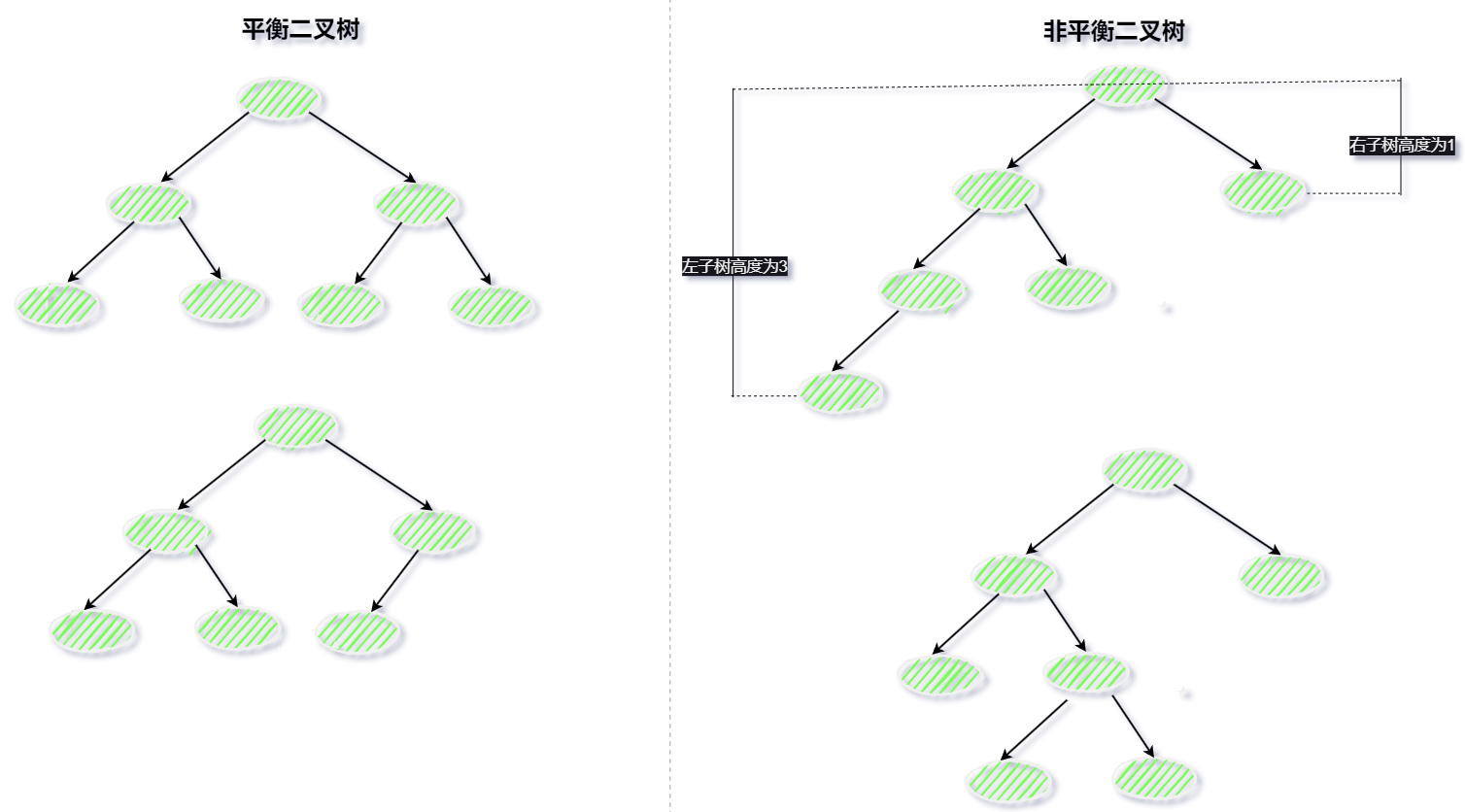
平衡二叉树保证了树的构造是保持平衡的,当插入或删除数据导致不满足平衡二叉树不平衡时,平衡二叉树会进行调整树上的节点来保持平衡。
B 树
数据在内存中存放是不可靠的,实际中会将例如商品表中的数据和索引存储在磁盘中;但磁盘相较于内存,读取数据的速度会慢上千百倍,所以应该尽量减少从磁盘中读取数据的次数;还有从磁盘读取数据时,都是按照磁盘块读取的,并不是一条记录一条记录读的;如果能将数据放进磁盘块中,那么一次磁盘读取操作就会读取更多的数据,超找数据的时间就会减低。如果用树这种数据结构作为索引的数据结构,那么每次查找数据就只需要从磁盘中读取一个节点(磁盘块)。而平衡二叉树每个节点只存储一个键值和数据,这样每个磁盘块就只能存一个键值和数据,大量数据存储的情况,就会出现二叉树节点多,高度高,导致查找数据进行的磁盘 IO 次数也随之变多,以至于查找数据的效率极具降低。如下图所示:
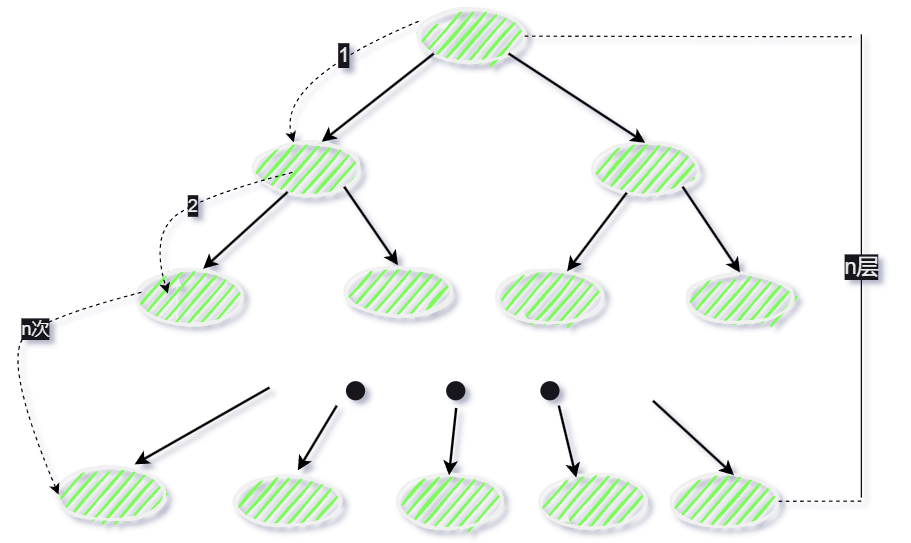
为了解决平衡二叉树的这个弊端,我们应该寻找一种单个节点可以存储多个键值和数据的平衡树,而 B 树就满足这种情况。
B 树(Balance Tree)即为平衡树的意思,如下是一个 B 树:
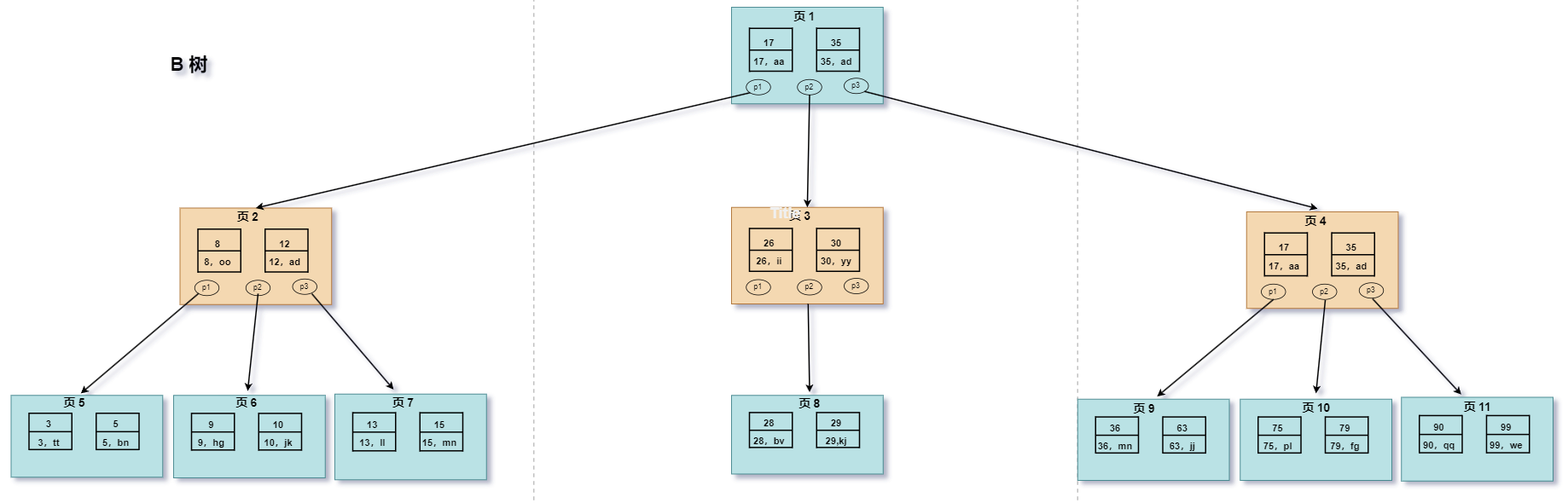
图中的 p 节点为指向子节点的指针。
图中的每个节点称为页,页就是我们上面说的磁盘块,在 MySQL 中数据读取的基本单位都是页。
从上图可以看出,B 树相对于平衡二叉树,每个节点存储了更多的键值(key)和数据(data),并且每个节点拥有更多的子节点,子节点的个数一般称为阶,上述图中的 B 树为 3 阶 B 树,高度也会很低。
基于这个特性,B 树查找数据读取磁盘的次数将会很少,数据的查找效率也会比平衡二叉树高很多。
假如我们要查找 id=28 的用户信息,那么我们在上图 B 树中查找的流程如下:
- 先找到根节点也就是页 1,判断 28 在键值 17 和 35 之间,那么我们根据页 1 中的指针 p2 找到页 3
- 将 28 和页 3 中的键值相比较,28 在 26 和 30 之间,我们根据页 3 中的指针 p2 找到页 8
- 将 28 和页 8 中的键值相比较,发现有匹配的键值 28,键值 28 对应的用户信息为(28,bv)
B+ 树
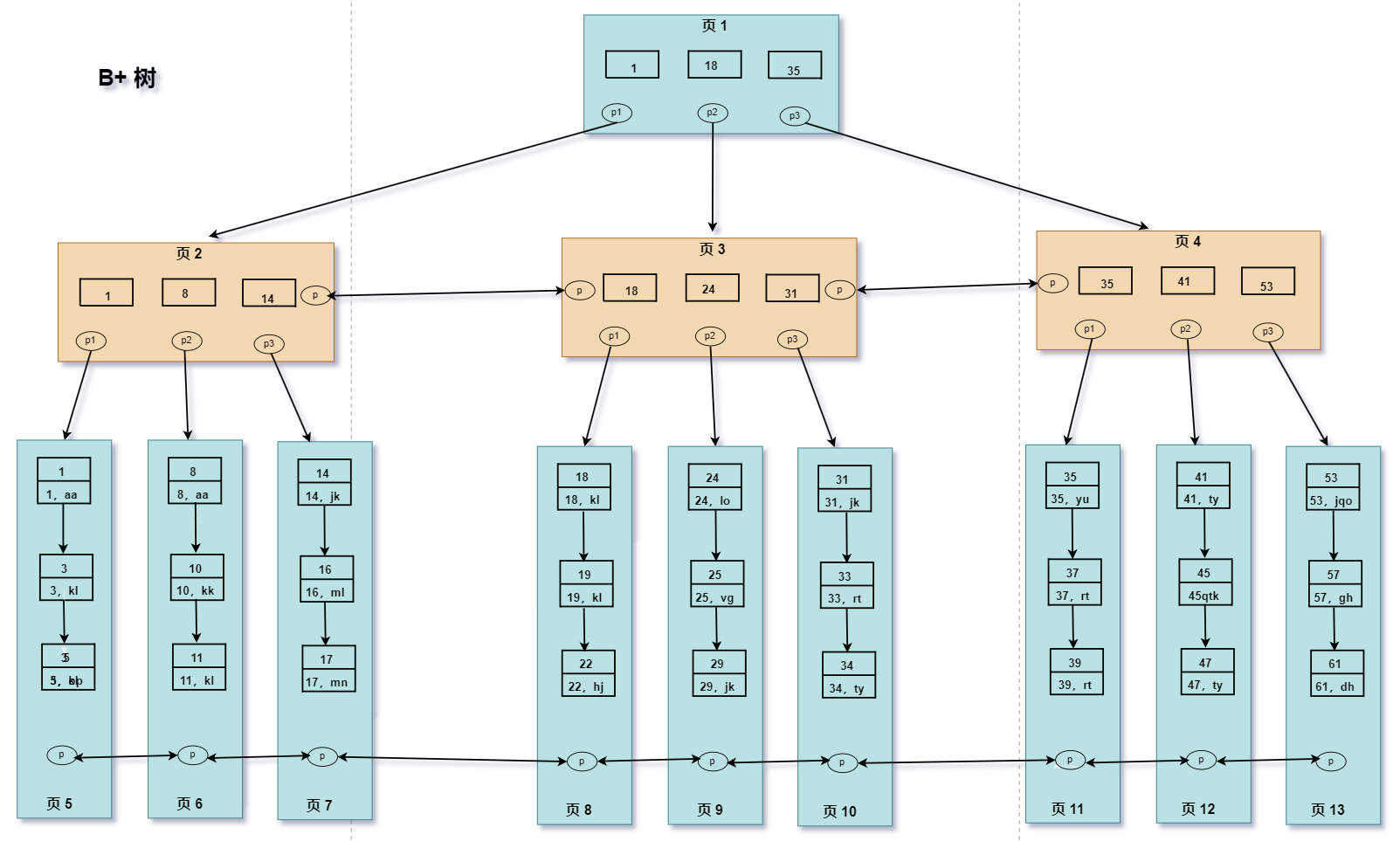
B+ 树与 B 树区别:
-
B+ 树非叶子节点上是不存储数据的,仅存储键值,而 B 树节点中不仅存储键值,也会存储数据。之所以这么做是因为在数据库中页的大小是固定的,InnoDB 中页的默认大小是 16KB。
如果不存储数据,那么就会存储更多的键值,相应的树的阶数(节点的子节点树)就会更大,树就会更矮更胖,如此一来我们查找数据进行磁盘的 IO 次数又会再次减少,数据查询的效率也会更快。
另外,B+ 树的阶数是等于键值的数量的,如果我们的 B+ 树一个节点可以存储 1000 个键值,那么 3 层 B+ 树可以存储 1000×1000×1000=10 亿个数据。
一般根节点是常驻内存的,所以一般我们查找 10 亿数据,只需要 2 次磁盘 IO。 -
因为 B+ 树索引的所有数据均存储在叶子节点,而且数据是按照顺序排列的。
那么 B+ 树使得范围查找,排序查找,分组查找以及去重查找变得异常简单。而 B 树因为数据分散在各个节点,要实现这一点是很不容易的。
B+ 树中各个页之间是通过双向链表连接的,叶子节点中的数据是通过单向链表连接的。
其实上面的 B 树我们也可以对各个节点加上链表。这些不是它们之前的区别,是因为在 MySQL 的 InnoDB 存储引擎中,索引就是这样存储的。也就是说上图中的 B+ 树索引就是 InnoDB 中 B+ 树索引真正的实现方式,准确的说应该是聚集索引。
通过上图可以看到,在 InnoDB 中,我们通过数据页之间通过双向链表连接以及叶子节点中数据之间通过单向链表连接的方式可以找到表中所有的数据。
MyISAM 中的 B+ 树索引实现与 InnoDB 中的略有不同。在 MyISAM 中,B+ 树索引的叶子节点并不存储数据,而是存储数据的文件地址。
跳表
聚集索引&非聚集索引
在 MySQL 中,B+ 树索引按照存储方式的不同分为聚集索引和非聚集索引。
只说 InnoDB 中的聚集索引和非聚集索引:
-
聚集索引(聚簇索引):以 InnoDB 作为存储引擎的表,表中的数据都会有一个主键,即使你不创建主键,系统也会帮你创建一个隐式的主键。
这是因为 InnoDB 是把数据存放在 B+ 树中的,而 B+ 树的键值就是主键,在 B+ 树的叶子节点中,存储了表中所有的数据。
这种以主键作为 B+ 树索引的键值而构建的 B+ 树索引,我们称之为聚集索引。 -
非聚集索引(非聚簇索引):以主键以外的列值作为键值构建的 B+ 树索引,我们称之为非聚集索引。非聚集索引与聚集索引的区别在于非聚集索引的叶子节点不存储表中的数据,而是存储该列对应的主键,想要查找数据我们还需要根据主键再去聚集索引中进行查找,这个再根据聚集索引查找数据的过程,称为回表。
聚集索引查找数据

以上是一个聚集索引。
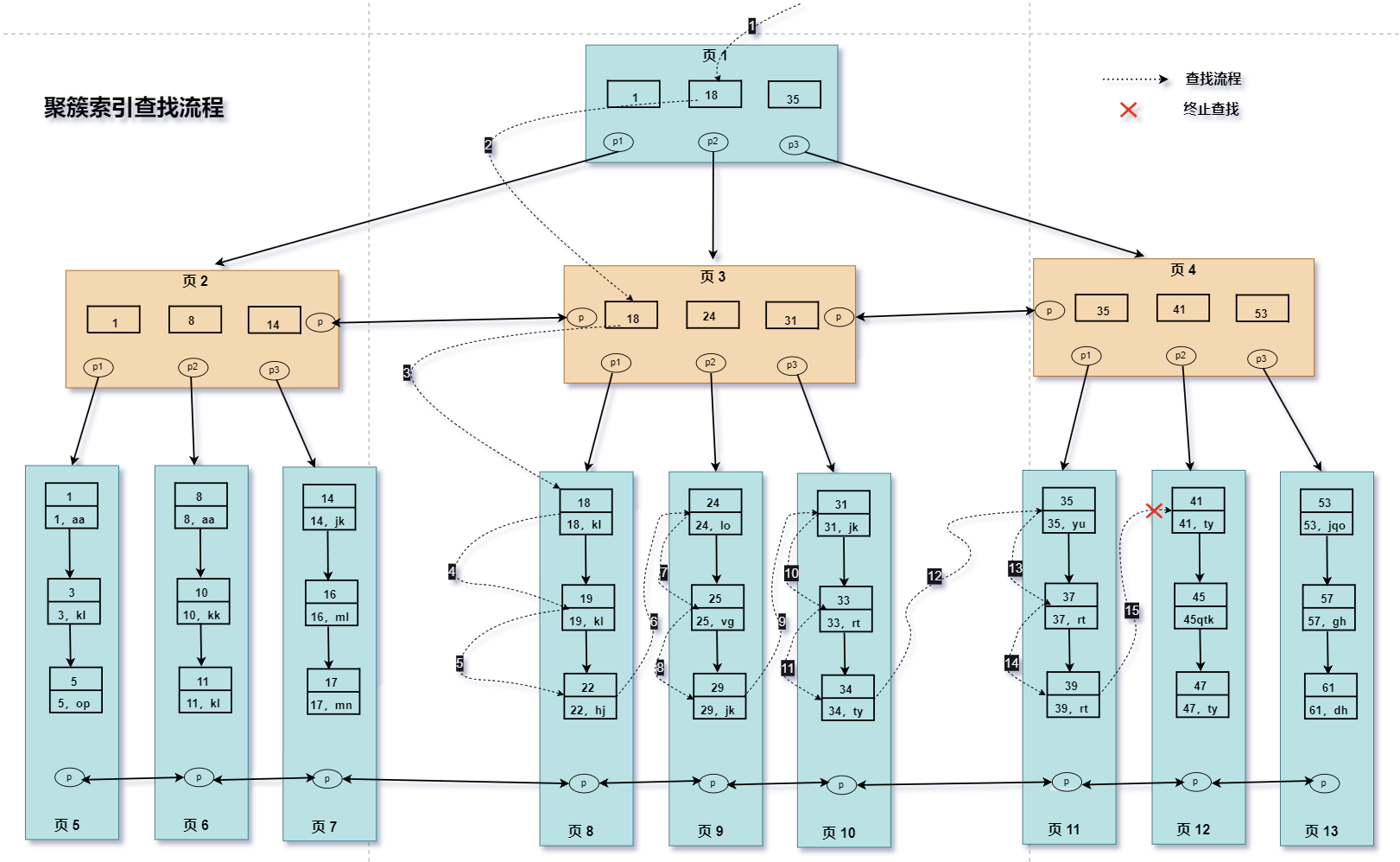
假设查询 id >= 18 并且 id < 40 的用户数据。对应的 sql 语句为:
select * from user where id >= 18 and id < 40
id 是主键,查询过程如下:
- 根节点一般情况下是在内存中,即:页 1 已存在于内存中,此时不需要到磁盘中读取数据,直接在内存中读取;
从内存汇总读取到页 1,要查找这个 id >= 18 and id < 40 的范围值,首先要找到 id = 18的键值;
从页 1 中可以找到键值 18,此时需要根据指针 p2,定位到页 3; - 从页 3 中查找数据,就需要用 p2 指针去磁盘中进行读取页 3;
从磁盘中读取页 3 后将 页 3 放入内存中,然后进行查找,看可以找到键值 18,之后拿到页 3 中的指针 p1,定位到页 8; - 同样的页 8 不存在内存中,需要从磁盘中将页 8 读取进内存中;
将页 8 读取到内存中后,页中的数据是链表进行链接的,而且键值是按照顺序存放,可以根据二分查找法定位到键值 18;
此时已经找到数据页,同时也找到了满足 id = 18 的数据,即:键值 18 对应的数据;
因是范围查找,而且此时所有的数据又都存在叶子节点,并且是有序排列的,因此,可以对页 8 中的键值依次遍历查找并匹配满足条件的数据;
一直遍历查找,找到键值为 22 的数据,之后页 8 中就没有数据了,此时需要用页 8 中的 p 指针去读取页 9 中的数据; - 而页 9 不在内存中,就又会加载页 9 到内存中,并通过和页 8 中一样的方式进行数据的查找(遍历、p 指针),知道将页 12 加载到内存中,发现 41 大于 40,这时就不满足条件了,结束查找。
- 最终我们找到满足条件的所有数据,总共 12 条记录:
(18,kl), (19,kl), (22,hj), (24,io), (25,vg) , (29,jk), (31,jk) , (33,rt) , (34,ty) , (35,yu) , (37,rt) , (39,rt)
查找详情流程图:
非聚集索引查找数据
非聚簇索引会根据二级索引找到主键,之后,拿着主键回表查询(和聚簇索引流程一致);
减少回表查询
索引覆盖
一个查询可以完全通过索引来执行,无需访问实际的数据行。即:一个索引包含了需要查询的所有字段 -> 联合索引
索引下推可以避免回表
尽可能把查询条件推到索引层面进行过滤,减少从磁盘读取的数据量。但是 ta 依赖于存储引擎层面
标签:分析,索引,查找,键值,二叉树,MySQL,数据,节点 From: https://www.cnblogs.com/zhzcc/p/18454042