为什么 MySQL 选择 B+树做索引？

标签：为什么 查询 叶子 索引 二叉树 MySQL 数据 节点

提到 MySQL 索引，相信使用过的小伙伴并不陌生，日常工作中，我们经常会加索引来提升查询效率，那么，为什么一个慢查询加上索引查询速度就能提升一个档次？索引后面的实现机制到底是什么？今天就让我们一起来探讨这个话题。

申明：本文说的磁盘是指普通的机械磁盘

一、索引是什么

比如阅读时，索引就是书的目录，如果想快速到达某一篇文章，通常会先查询目录找到页码，然后通过页码找到文章。

如果对数据库比较熟悉的话，那么就能很好的知道，索引就是数据库的目录，当数据表的数据成百万，千万级时，要想快速定位数据行时，就需要这样一张数据目录。因此，索引的本质就是选择一种合理的数据结构，在执行效率方面能尽可能地高，在存储空间方面，又不要消耗太多的内存。

那么，选择哪一种数据结构呢？

二、索引数据结构

用于索引的数据结构有多种，这里介绍 3 种常见且简单的数据结构：哈希表、有序数组和搜索树。

2.1、哈希表

哈希表是一种以 key-value 键值对存储数据的结构，比如：java 的 hashmap， redis 的 key-value 都是这样一种形式。hash 表的实现思路也很简单：用一个哈希函数把 key 换算成数组确定的位置，然后把 value 放在数组的这个位置。

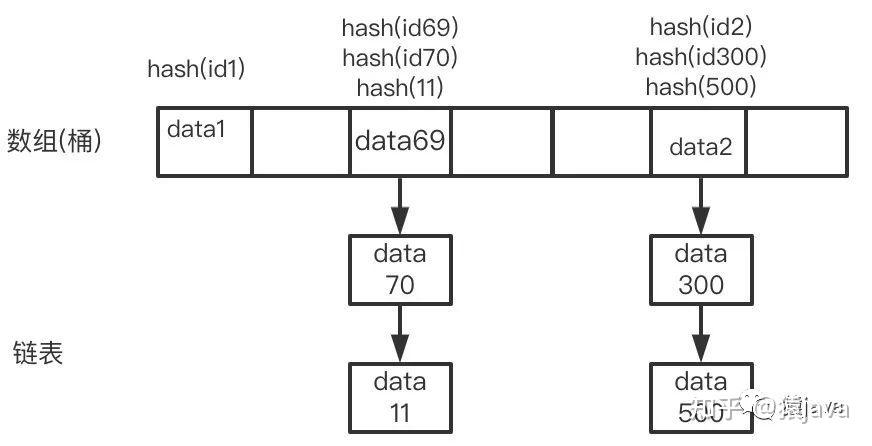
从上图我们可以看到，当 key 的 hash 值相同的时候，会采用链表的方式把 value 串起来。

hash 表的问题随着数据量的增多，不同 key 经过哈希计算后结果一样，这种情况叫做 hash 碰撞。处理 hash 碰撞的一种方法是链表，但是当数据量比较大时，链表的长度还是会比较大，性能开销就在链表查询上。哈希表是散列存储，因此这种结构适用于只有等值查询的场景，比如 Memcached 及其他一些 NoSQL 引擎。

2.2、有序数组

如下图，如果数据按照 id 的升序存放到数组中，就形成了一个有序数组，这样既能根据等值查询，也方便范围查询。

有序数组问题如果仅仅看查询效率，有序数组是比较好的数据结构，但如果有数据的插入和删除，插入和删除点后面的数据需要移动，所以整体性能会下降，因此，有序数组只适合静态存储引擎。

2.3、搜索树

2.3.1 二叉树(Binary Tree)

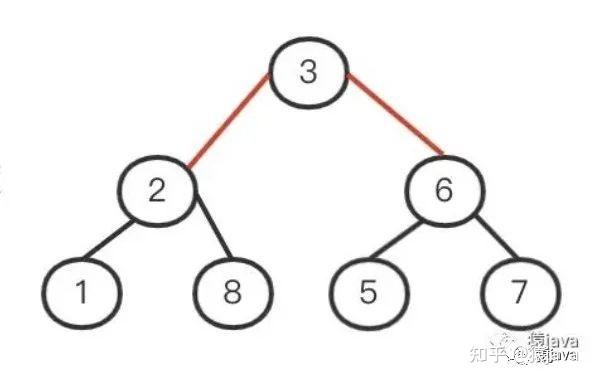
每个节点最多只能有两个子节点就是二叉树。

二叉树的定义很简单，它是很多其他搜索树的基础，下面给出一张二叉树的示意图：

 

2.3.2 二叉查找树

二叉查找树(Binary Search Tree)，是一种特殊的二叉树，其特点如下：左子树节点比父节点小，右子树节点值比父节点大。

 

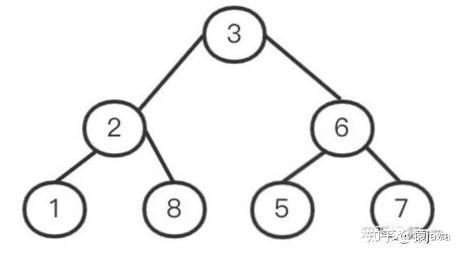
根据二叉搜索树的特点可以使用二分查找法，比如，在二叉查找树中查询 5。

• 首先，从根节点开始遍历，5 > 3，可以定位 5 在节点 3 的右子树。
• 其次，遍历节点 3 的右子树，5 < 6，可以定位 5 在节点 6 的左子树。
• 最后，遍历节点 6 的左子树，因为左子树只有一个节点 5，5=5，即目标值。

 

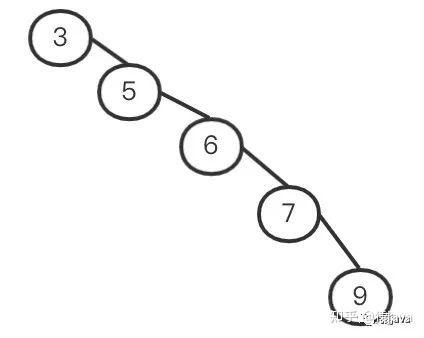
二叉查找树的问题

二叉查找树是一棵二叉树，当数据是有序增长，在极端情况下，整个二叉搜索树就会变成一棵斜树，这样就退化成了链表结构。如下图所示：

 

2.3.3 平衡二叉树

平衡二叉树(Balanced Binary Search Tree)，又被称为 AVL 树，它是为了解决二叉树退化成链表而诞生的，其特点如下：每个节点的左子树和右子树的高度差至多等于 1。

为了解决二叉搜索树在极情况下变成斜树的问题，平衡二叉树增加了左右子树的高度差小于等于 1。

因为平衡二叉树追求绝对严格的平衡，平衡条件必须满足左右子树高度差不超过 1，该规则在于频繁的插入、删除等操作的情景性能肯定会出现问题，因此诞生了红黑树。

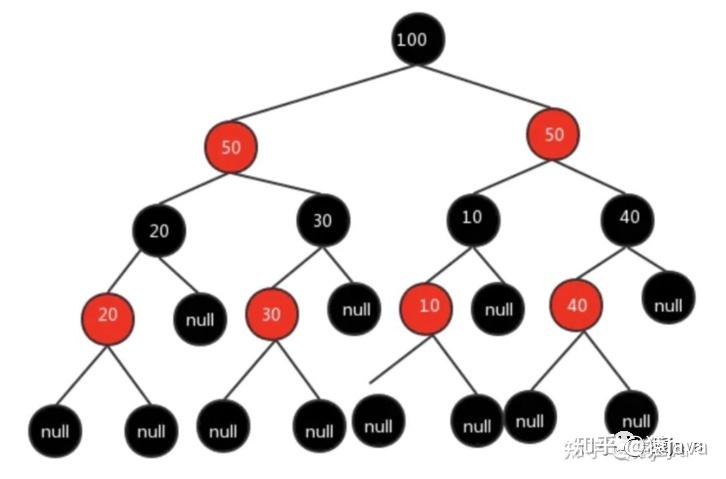
2.3.4 红黑树

红黑树是一种特殊的平衡二叉树，主要特点如下：

• 具有二叉树所有特点。
• 每个节点要么是黑色，要么是红色。
• 根节点是黑色。
• 每个叶子节点（NIL）是黑色。
• 每个红色结点的两个子结点一定都是黑色。
• 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

 

如下图，给出了一棵 红黑树示意图：

 

2.3.5 B-树(Balance Tree)

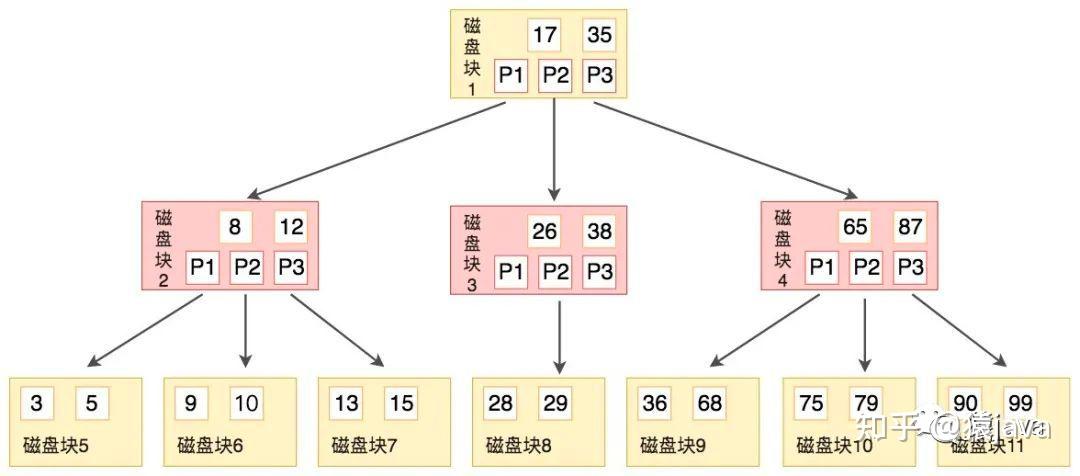
B-树，Balance Tree，也就是平衡的多路搜索树（注意：这里的“-”只是一个连接符，千万不要读成B减树），它的高度远小于平衡二叉树的高度。在文件系统和数据库系统中的索引结构经常采用 B 树来实现，特点如下：

• 定义任意非叶子结点最多只有M个叶子结点；且M>2；
• 根结点的叶子节点数为[2, M]；
• 除根结点以外的非叶子结点的叶子结点数为[M/2, M]；
• 每个结点存放至少M/2-1（取上整）和至多M-1个关键字；
• 非叶子结点的关键字个数 = 指向叶子节点的指针个数-1；

 

如下图，给出了一棵 B-树示意图：

 

2.3.6 B+树

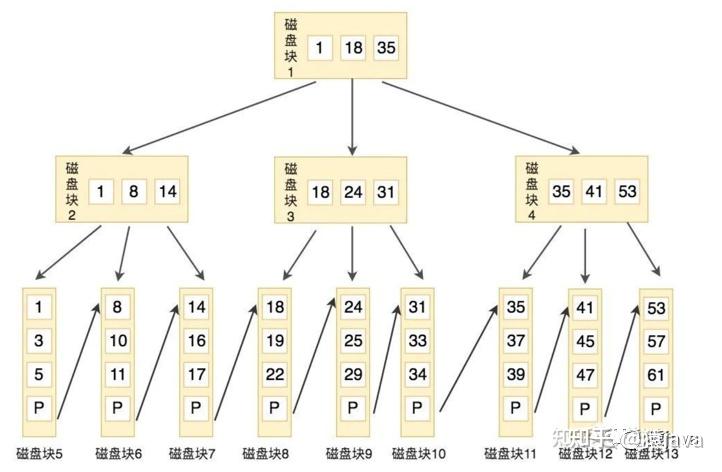
B+树是基于 B-树优化而来，发明于 1972 年，B+树特点：

• 每个节点中子节点的个数不能超过 m，也不能小于 m/2；
• 根节点的子节点个数可以不超过 m/2，这是一个例外；
• m 叉树只存储索引，并不真正存储数据，这个有点儿类似跳表；
• 通过链表将叶子节点串联在一起，这样可以方便按区间查找；
• 一般情况，根节点会被存储在内存中，其他节点存储在磁盘中。

B+树和 B-树的差异点：

• B+树的数据保存在叶子节点，并且组成了一个增序的链表，B-树的所有节点都保存了数据；
• B+树叶子节点的数据是有序链表，因此支持 range-query范围查询，而 B-树不支持；
• B+树叶子节点的数据是有序双向链表，方便asc升序查询和desc降序查询；

 

如下图，给出了一棵 B+树示意图：

 

到此，我们把索引中几种常见的数据结构分析完成。

 

三、B+树如何实现索引

鉴于目前 MySQL最主流的引擎是 MyISAM 和 InnoDB，因此我们就从这两个引擎分别讲解。

3.1 MyISAM 引擎

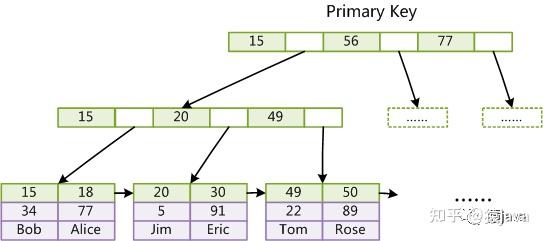
MyISAM 采用的非聚簇索引，B+树的非叶子节点存储索引值和指向子节点的指针，叶子节点上存放的是索引值和数据在磁盘上的物理地址，所以通过索引定位到数据地址后，需要到磁盘上回表获取数据，索引模型示意图如下：

 

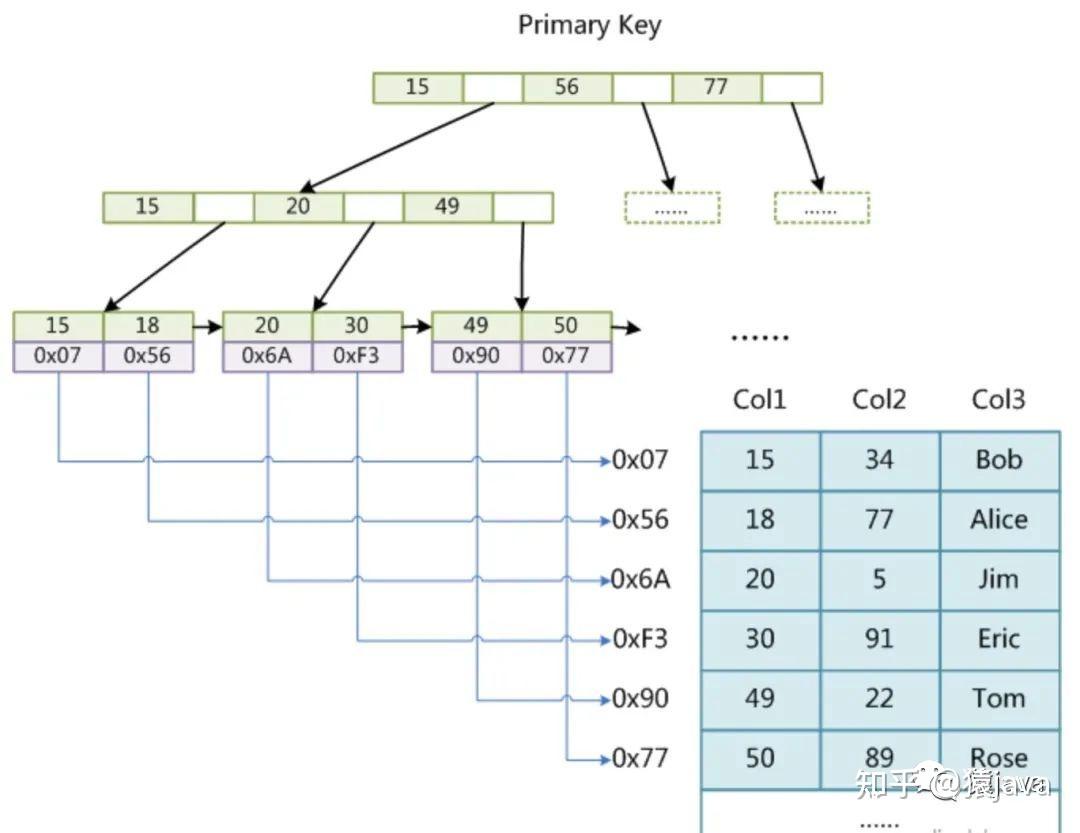
所以，在 MyISAM引擎中，B+树的叶子节点不存储数据，而是数据的物理地址，不管是主键索引还是非主键索引，都需要回表获取数据。

 

3.2 InnoDB 引擎

InnoDB 采用的聚簇索引，B+树的非叶子节点（内部节点）存放的是索引值和指向子节点的指针，叶子节点上存放的是索引值和数据。每一个索引在 InnoDB 里面对应一棵 B+ 树。

非聚簇索引，B+树的非叶子节点存储索引值和指向子节点的指针，叶子节点存放的是索引值和聚簇索引值。因此非聚簇索引需要先遍历非聚簇索引 B+树定位到聚簇索引的值，再到聚簇索引上回表获取数据。聚簇索引的优点：可以避免每棵索引树上都存放数据，使得在相同的内存空间下存放的更多的索引节点，减少磁盘 IO。

聚簇索引示意图如下：

非聚簇索引示意图如下：

 

 

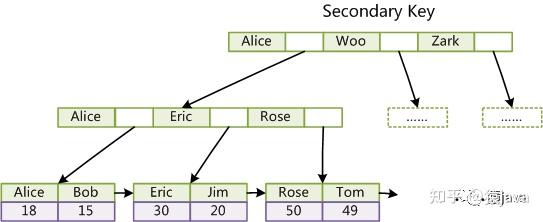
所以，在 InnoDB中，如果是通过主键索引查询的话，可以直接从叶子节点拿到数据。如果是通过非聚簇索引查询，则需要根据非聚簇索引定位到主键索引，然后再从叶子节点拿到数据。

四、几个常见概念

4.1 聚簇索引

在 InnoDB 里，主键索引也被称为聚簇索引（clustered index），主键索引的叶子节点存放的是整行数据，索引和数据存储在一起。一个表中聚簇索引只能有一个。

4.2 非聚簇索引

在 InnoDB 引擎里，非主键索引也被称为二级索引（secondary index），非主键索引的叶子节点内容是主键的值，索引和数据分开存储。

在 MyISAM 引擎中，使用的是非聚簇索引。

4.3 索引覆盖

在当前索引树上能直接查找所需结果，不需要回表，这就是索引覆盖。

比如上面的案例：select id from user where age = 30 and sex = '男'; 因为 id 已经在当前索引的叶子节点，所以不需要到聚簇索引上回表，因此这就是一个索引覆盖的场景。由于覆盖索引可以减少树的搜索次数，显著提升查询性能，所以使用覆盖索引是一个常用的性能优化手段。

4.4 联合索引

联合索引是指：将表中多个字段联合组合成一个索引，比如：index(age, sex)

那么联合索引是如何用 B+树来实现的呢？

场景：查询用户表中年龄为 30 岁的男性表结构：

mysql> create table user(
id int primary key,
name varchar(16),
age int not null,
sex varchar(4) not null,
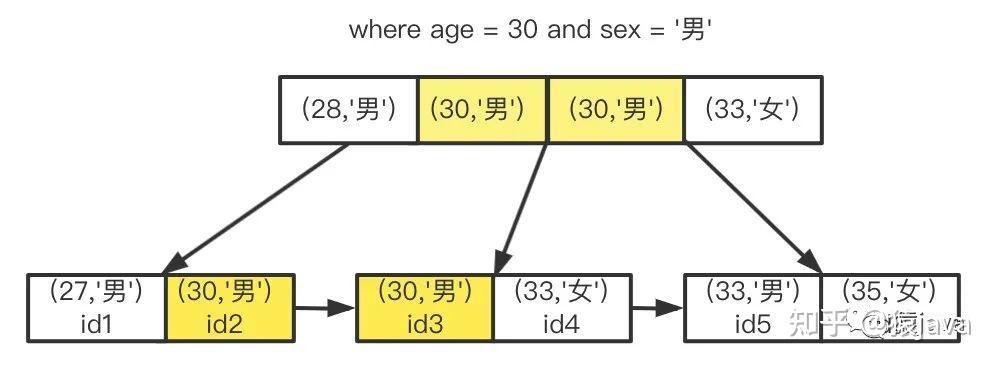
index(age, sex)) engine=InnoDB;

联合索引在 B+树索引模型示意图如下：

 

查询分析：

• 首先，从根节点根据组合索引里面的所有字段进行精确匹配查到到 age=30 and sex='男'的记录有两条；
• 然后，获取 id2 和 id3 两个节点中指向子节点的指针，定位到子节点，再定位到叶子节点，从叶子节点中拿到聚簇索引的值 id2 和 id3；
• 最后，到聚簇索引上遍历 id2 和 id3，直到叶子节点上获取目标数据；

 

4.5 最左前缀原则

在日常的工作中，需要根据不同的条件进行数据查询，比如上面的用户表，有根据 age 和 sex 查询，有根据 name 和 age 查询，也有根据 name 和 sex 查询，各种查询组合，因此，需要为每种条件创建一个索引吗？

答案是不一定。

B+树可以利用索引的“最左前缀”来定位记录。最左前缀可以是联合索引的最左 N 个字段，也可以是字符串索引的最左 M 个字符 比如：对于以下查询条件，联合索引 index(a, b, c)都可以匹配索引

• where a = ?
• where a = ? and b = ?
• where a = ? and b = ? and c = ?

但是，对于 where a = ？and c = ? 只有 a条件可以匹配，c 条件无法匹配

为了更好地说明最左前缀原则，下面给出一个实例分析：

场景：查询用户表中姓刘，性别为男性的用户。

联合索引：index(name, sex)

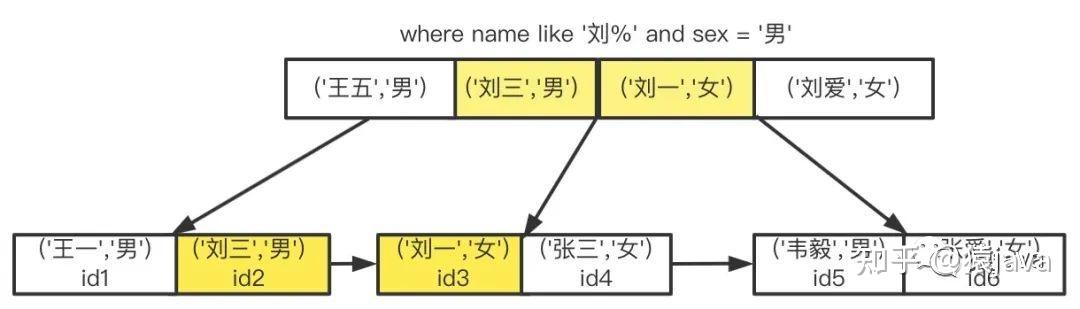
B+树索引模型示意图如下：

 

查询分析：

• 首先，从根节点查到第一个'刘'开头的记录是id2，然后向后遍历，直到不满足条件为止，最后结果id2，id3两条；
• 然后，获取指向子节点的指针，定位到子节点，一直到叶子节点，接着比较第2个字段 sex='男'，定位到 id2；
• 最后，根据id2到聚簇索引上遍历，直到叶子节点上获取目标数据；

 

4.6 索引下推

从上面的查询分析可以看到：索引前缀原则，查询条件 name like '刘%' and sex = '男'，只用到了联合索引中的 name字段，那么 sex 条件没有用到，索引会怎么处理呢？

这个就是 MySQL5.6 引入的索引下推机制，根据 where name like '刘%' 可以定位一批数据，假定这批数据为 data，然后对于条件 sex = '男' ，会从 data数据中再筛选符合数据，这样就减少了全表扫描，减少了回表的次数，降低了磁盘IO。

4.7 索引维护

从上文的分析可以知道：每一个索引在 InnoDB 里面对应一棵 B+ 树。B+ 树为了维护索引有序性，在数据更新时会进行必要的维护，因此索引字段的大小直接索引维护的成本，从而影响 SQL语句的性能。

五、问题

 

问题 1：为什么 MySQL选 B+树而不选红黑树做索引？

MySQL 的数据都是存放在磁盘，因此磁盘 IO 是 MySQL 的性能瓶颈，而二叉树，二叉搜索树，二叉平衡树，红黑树 都属于二叉树，当 MySQL 表中的数据量比较大时，索引的体积也会很大，树高就会很大，内存放不下的需要从磁盘读取，树的层次太高的话，读取磁盘的次数就多了，影响 MySQL 的使用性能。B+ 树是多叉树，能够用有限的树高存储大量的数据，它能够很好地配合磁盘的读写特性，减少单次查询的磁盘访问次数。

问题 2：为什么 MySQL 选 B+树而不选B-树做索引？

从上文对B+树和B-树的比较可以发现，B-树所有的节点都存放数据，而 B+树只有叶子节点存放数据，所以在一定意义上 B+树存储的容量比 B-树大，另外，B+树叶子节点的数据成有序链表，支持范围查询，而B-树不支持，所以选B+树的优点就显现出来了，B+ 树通过存储在磁盘的多叉树结构，做到了时间、空间的平衡，既保证了执行效率，又节省了内存。

问题 3：一个三层的 B+树可以存放多少行数据呢？

在 InnoDB 存储引擎里面，最小的存储单元是页（page），一个页的大小是 16KB，也就是一个节点的大小。根据上文，非叶子节点保存的是索引值和指针，假设索引 id 是 long类型，占 8个byte，指针占 6 byte，所以，根节点可以存放 16KB / (8 + 6) = 1170 个索引值，因此就有1170个指针，假设一条数据的大小是1K，因此叶子节点可以存放 16Kb/1K = 16条数据，所以3层的B+树可以存放 1170 * 1170 * 16 = 21902400行记录，所以，一个三层的 B+树可以存放 2000万左右的数据。

 

六、LSM-Tree

B+树的数据都存储在叶子节点中，而叶子节点一般都存储在磁盘中，我们可以发现 B+索引树上相邻的两个节点，其实可能在物理磁盘上不相邻的，因此，每次插入的新数据都需要随机写入磁盘，而磁盘的随机写入的性能非常慢，因此有没有更好的数据结构来解决这个问题？答案是：LSM-Tree

定义

LSM-Tree：Log Structured Merge Trees 日志结构组合树。LSM 树也是近年来许多火热的 NoSQL 数据库中使用的检索技术。比如，日志系统、监控系统。这些应用场景有一个共同的特点：数据会持续地大量生成，而且相比于检索操作，它们的写入操作会非常频繁。另外，即使是检索操作，往往也不是全范围的随机检索，更多的是针对近期数据的检索。

LSM-Tree 的实现机制

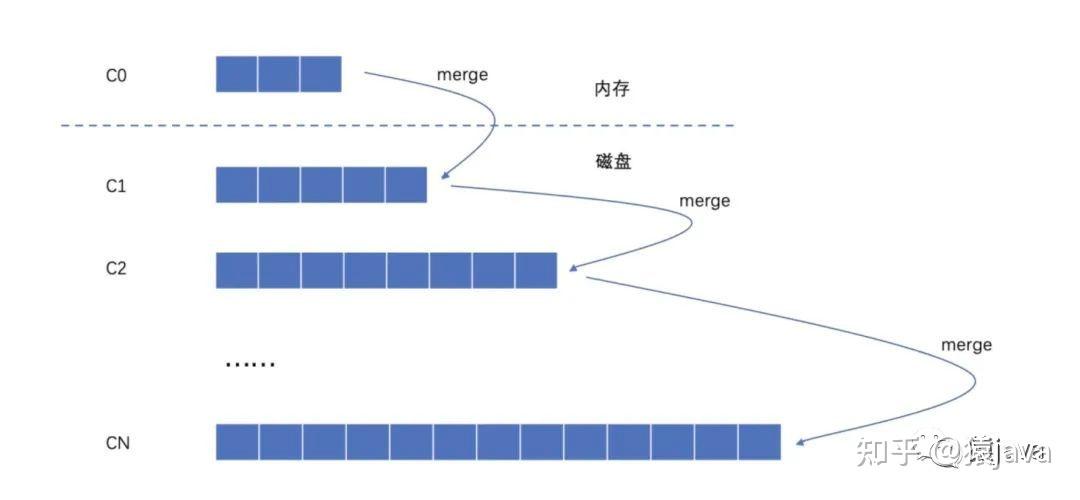
LSM-Tree 采用的是磁盘顺序写，它是一种多层结构，最上层 C0 位于内存中，存储最近写入的 key-value 数据，下面的 C1~CN 是位于磁盘中，每一层按 key 的字典顺序进行排序。

写操作：先写 C0 层，当 C0 层数据达到阈值就会把数据合并到 C1 层(归并排序)，C1 达到阈值，又把数据合并到 C2，以此类推。读请求：先读 C0 层，因为这个层里面的数据是最新的。如果 C0 没有，则一次往下找。

LSM-Tree 示意图

使用场景

HBase NoSQL 数据库，LevelDB

通过今天对 MySQL 索引机制，我们分析和对比了很多的数据结构，同时我们也会发现，检索是海量数据查询的一个重要课题，针对不同的场景，我们需要采用不同的数据结构。

标签：为什么,查询,叶子,索引,二叉树,MySQL,数据,节点
From： https://www.cnblogs.com/jiaodaoniujava/p/17636651.html