数据结构之栈和队列算法题

一：有效括号数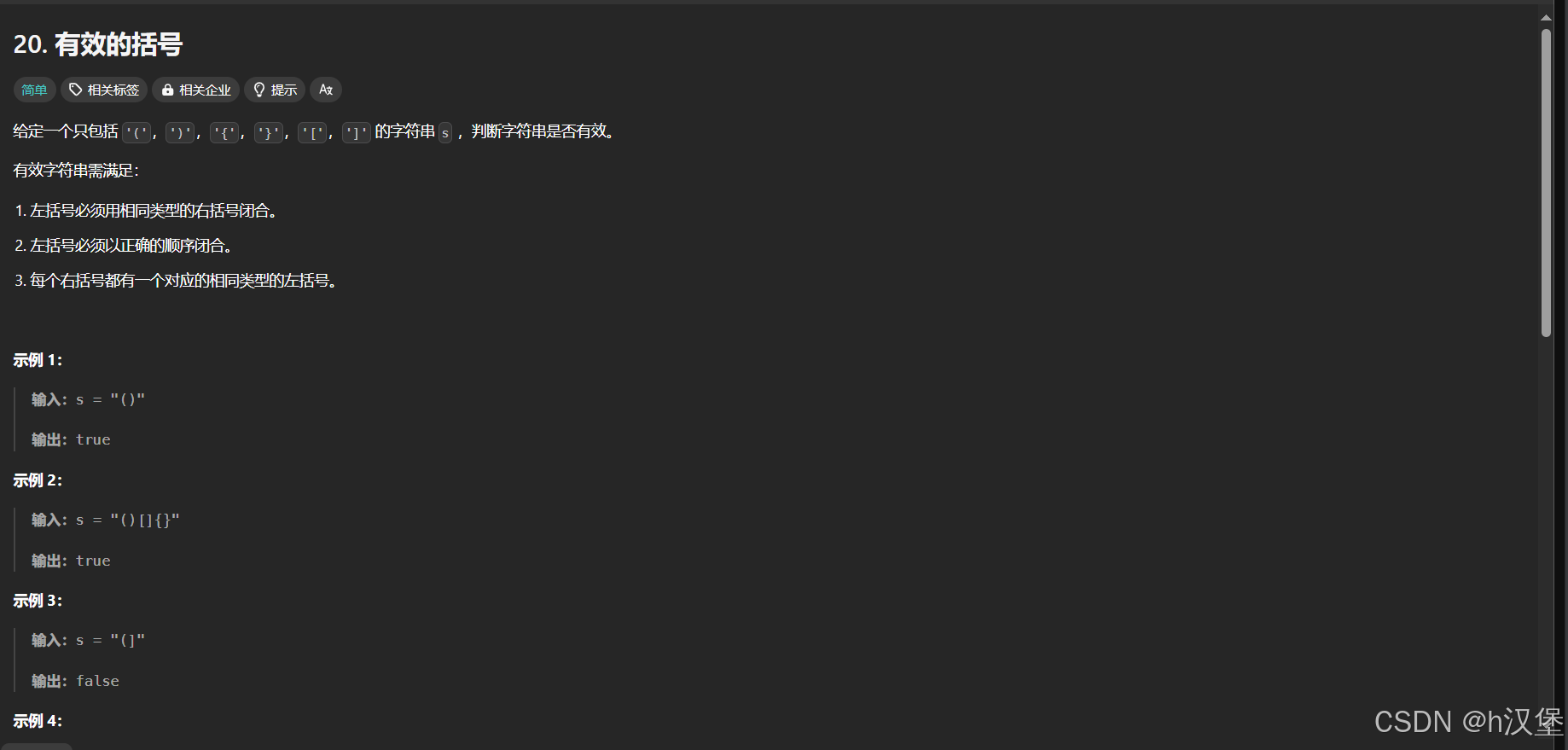

学了栈之后这一题就比较简单了。

思路：1、左括号进栈 2、右括号出栈匹配。

完整代码：

因为使用C语言写的，所以里面包含了栈的实现

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int STDataType;
typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;
}ST;

void StackInit(ST* st);

void StackPush(ST* st, STDataType x);

void StackPop(ST* st);

STDataType StackTop(ST* st);

bool StackEmpty(ST* st);

void StackDestroy(ST* st);

int StackSize(ST* st);


void StackInit(ST* st)
{
	st->a = NULL;
	//top 表示栈顶元素的下一个
	st->capacity = st->top = 0;
}

void StackPush(ST* st, STDataType x)
{
	assert(st);
	if (st->top == st->capacity)
	{
		int newcapacity = st->capacity == 0 ? 4 : st->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(st->a, newcapacity*sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("malloc fail!!");
			exit(1);
		}
		st->a = tmp;
		st->capacity = newcapacity;
	}
	st->a[st->top++] = x;
}

void StackPop(ST* st)
{
	assert(st);

	assert(!StackEmpty(st));

	st->top--;
}

STDataType StackTop(ST* st)
{
	assert(st);
	assert(!StackEmpty(st));

	return st->a[st->top - 1];
}

bool StackEmpty(ST* st)
{
	assert(st);

	return st->top == 0;
}

void StackDestroy(ST* st)
{
	assert(st);

	free(st->a);
	st->a == NULL;
	st->capacity = st->top = 0;
}

int StackSize(ST* st)
{
	assert(st);
	return st->top;
}

bool isValid(char* s) {
    ST st;
    StackInit(&st);
    while(*s)
    {
        if(*s=='{'
        || *s=='('
        || *s=='[')
        {
            StackPush(&st,*s);
        }
        else
        {
            if(StackEmpty(&st))
            {
                StackDestroy(&st);
                return false;
            }
            char c = StackTop(&st);
            StackPop(&st);
            if((c == '{' && *s != '}')
            || (c == '(' && *s != ')') 
            || (c == '[' && *s != ']'))
            {
                StackDestroy(&st);
                return false;
            }
        }
        s++;
    }
    bool ret = StackEmpty(&st);
    StackDestroy(&st);
    return ret;
}

二：用队列实现栈

首先说明一点，这只是对栈和队列熟练度的考察，并不是栈的更好地实现方式。

思路：两个队列，保证有一个队列为空，然后其余操作基于空队列实现。

画图分析：

完整代码：

typedef int QDatatype;

typedef struct QueueNode {
	QDatatype data;
	struct QueueNode* next;
}QueueNode;

typedef struct Queue {
	struct QueueNode* head;
	struct QueueNode* tail;
}Queue;


void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDatatype x);
void QueuePop(Queue* pq);
QDatatype QueueFront(Queue* pq);
QDatatype Queueback(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;
}
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->head;
	while (cur)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
}
void QueuePush(Queue* pq, QDatatype x)
{
	assert(pq);
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("malloc fail!!");
		exit(1);
	}
	else
	{
		newnode->next = NULL;
		newnode->data = x;
	}
	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(pq->head != NULL);

	QueueNode* del = pq->head;
	pq->head = del->next;
	free(del);
	del = NULL;
	if (pq->head == NULL)
	{
		pq->tail = NULL;
	}
}
QDatatype QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->head != NULL);

	return pq->head->data;
}
QDatatype Queueback(Queue* pq)
{
	assert(pq);
	assert(pq->head != NULL);

	return pq->tail->data;
}
int QueueSize(Queue* pq)
{
	assert(pq);
	int cnt = 0;
	QueueNode* cur = pq->head;
	while (cur)
	{
		cnt++;
		cur = cur->next;
	}
	return cnt;
}
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}


typedef struct {
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() 
{
    //不能直接创建结构体，出函数栈帧销毁
    MyStack* st = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&st->q1);
    QueueInit(&st->q2);
    return st;
}

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

int myStackPop(MyStack* obj) {
	//判空
	Queue *Empty = &obj->q1;
	Queue *NonoEmpty = &obj->q2;
	if (!QueueEmpty(Empty))
	{
		Empty = &obj->q2;
		NonoEmpty = &obj->q1;
	}
	//出队列，入另外一个队列
	while (QueueSize(NonoEmpty) > 1)
	{
		QDatatype data = QueueFront(NonoEmpty);
		QueuePush(Empty, data);
		QueuePop(NonoEmpty);
	}
	//剩余一个元素
	QDatatype data = QueueFront(NonoEmpty);
	QueuePop(NonoEmpty);
	return data;
}

int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->q1))
    {
        return Queueback(&obj->q1);
    }
    else
    {
        return Queueback(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) {
    return (QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2));
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

/**
 * Your MyStack struct will be instantiated and called as such:
 * MyStack* obj = myStackCreate();
 * myStackPush(obj, x);
 
 * int param_2 = myStackPop(obj);
 
 * int param_3 = myStackTop(obj);
 
 * bool param_4 = myStackEmpty(obj);
 
 * myStackFree(obj);
*/

三：用栈实现队列

这一题就是反过来用栈实现队列，要实现后进先出。

思路：两个栈pushst popst 然后往pushst里面push ，每当要出队列或者要去队头数据时，就返回popst的栈顶数据，如果popst为空，就一口气把pushst里面的数据全塞进去。

就不画图了

完整代码：

栈的实现在上面有，不重复拷贝了。

typedef struct {
    ST pushst;
    ST popst;
} MyQueue;


MyQueue* myQueueCreate() {
    MyQueue* pq = (MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&pq->pushst);
    StackInit(&pq->popst);
    return pq;
}

void myQueuePush(MyQueue* obj, int x) {
    StackPush(&obj->pushst,x);
}

int myQueuePop(MyQueue* obj) {
    if(StackEmpty(&obj->popst))
    {
        while(!StackEmpty(&obj->pushst))
        {
            StackPush(&obj->popst,StackTop(&obj->pushst));
            StackPop(&obj->pushst);
        }
    }
    int frontstack = StackTop(&obj->popst);
    StackPop(&obj->popst);
    return frontstack;
}

int myQueuePeek(MyQueue* obj) {
    if(StackEmpty(&obj->popst))
    {
        while(!StackEmpty(&obj->pushst))
        {
            StackPush(&obj->popst,StackTop(&obj->pushst));
            StackPop(&obj->pushst);
        }
    }
    return StackTop(&obj->popst);
}

bool myQueueEmpty(MyQueue* obj) {
    return StackEmpty(&obj->popst) && StackEmpty(&obj->pushst);
}

void myQueueFree(MyQueue* obj) {
    StackDestroy(&obj->popst);
    StackDestroy(&obj->pushst);
    free(obj);
}

四：环形队列（环形缓冲器）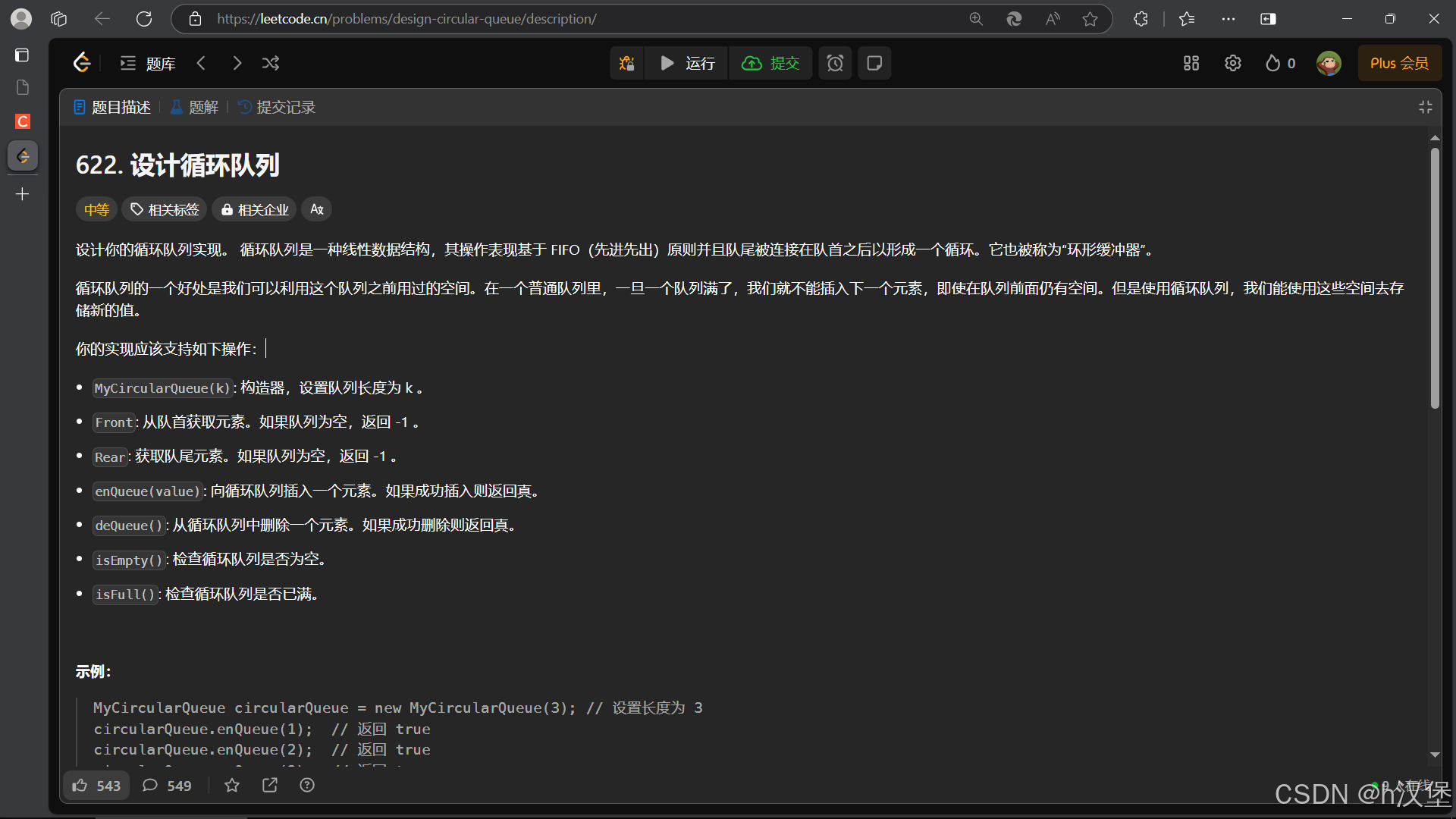

这里给大家贴一张图：

（数组实现）思路：创建K（存有效数据的大小）+1的长度，两个指针（严格来讲应该是下标）指向头和尾。然后用%操作实现循环。

具体请看下面画图分析

画图分析：

完整代码：

typedef struct {
    int* a;
    int tail;
    int head;
    int k;
} MyCircularQueue;

bool myCircularQueueIsEmpty(MyCircularQueue* obj);
bool myCircularQueueIsFull(MyCircularQueue* obj);
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* cp =(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    cp->a =(int*)malloc(sizeof(int)*(k+1));
    cp->tail = 0;
    cp->head = 0;
    cp->k = k;
    return cp;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
    return false;
    else
    {
        obj->a[obj->tail] = value;
        ++obj->tail;
        obj->tail %= (obj->k+1);
        return true;
    }
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    return false;
    else
    {
        obj->head++;
        obj->head %= (obj->k+1);
        return true;
    }
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    return -1;
    return obj->a[obj->head];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
    return -1;
    return obj->a[(obj->tail+obj->k)%(obj->k+1)];
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->head == obj->tail;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->tail+1)%(obj->k+1) == obj->head;
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

  完