目录
Overview
输出形式:早物化与晚物化(OLAP一般都是晚物化)
代价分析:一般用IO次数计算(最终结果可能落盘,也可能不落盘,所以我们只计算输出结果之前的IO次数)。
Join左边称为外表(Outer Table),右边称为内表(Inner Join),外表一般是小表。

Nested Loop Join
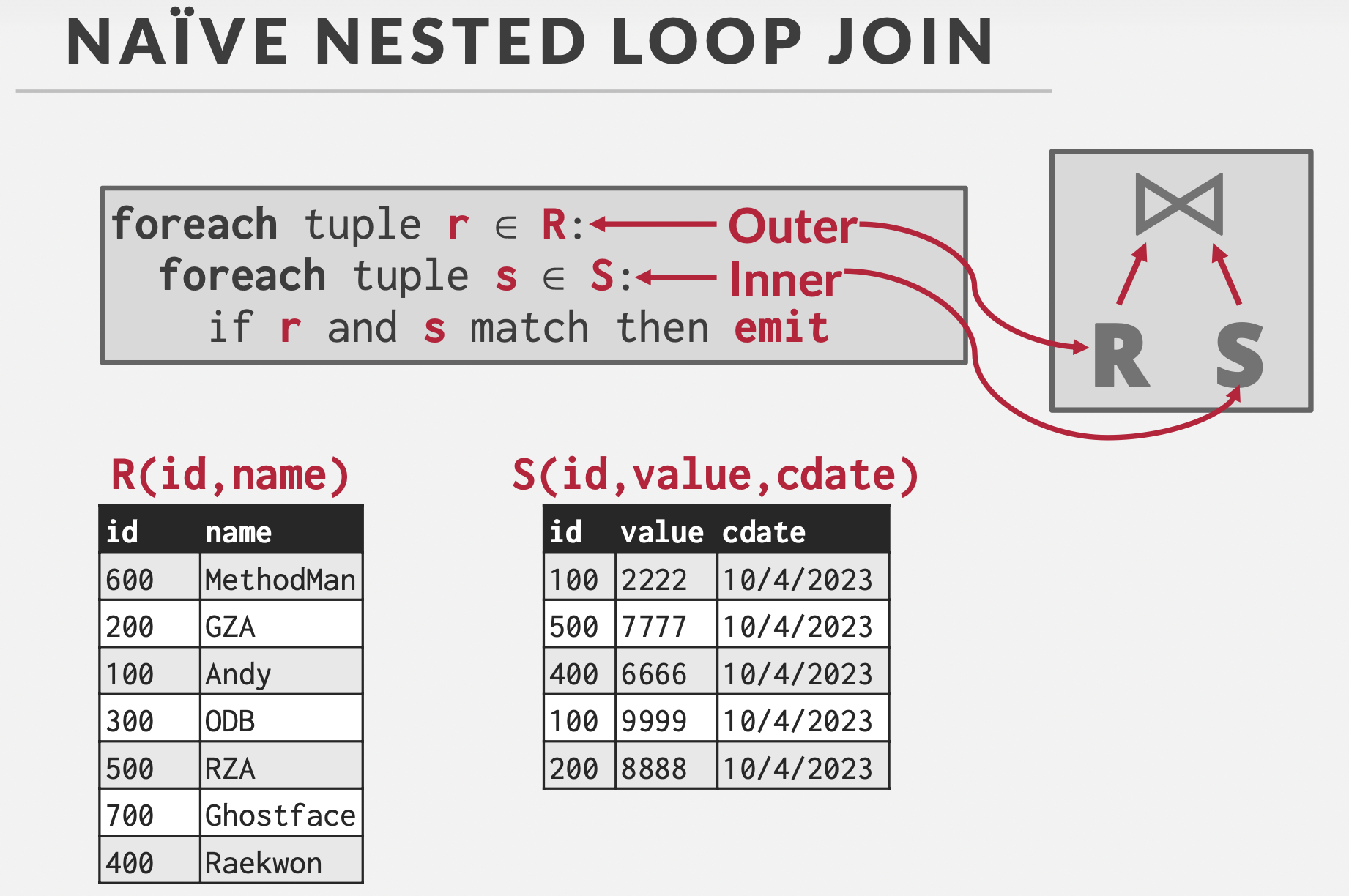
Naïve
前提:缓冲区大小为3,一个外表输入,一个内表输入,一个输出。
基本思想:双重循环,对每一个元组(Tuple)进行配对,读取S表m次。
Cost:\(M+(m*N)\)

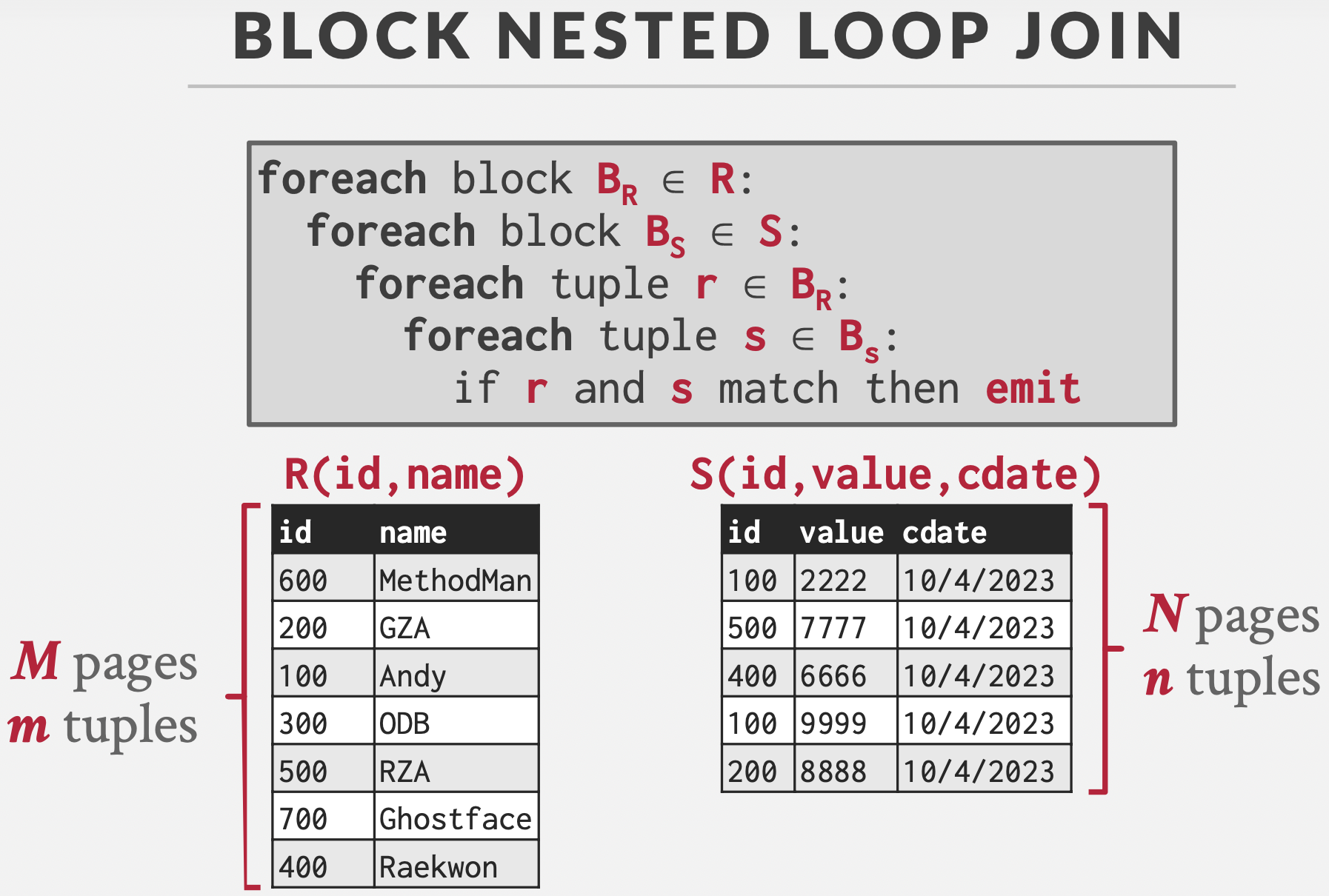
Block
前提:缓冲区大小为3,一个外表输入,一个内表输入,一个输出。
基本思想:双重循环,对每一个块(Block,同页Page)内进行配对,所以读取S表M次。
Cost:\(M+(M*N)\)
如果缓冲区容量为B,即可以容纳B个块(页),B-2个块用于外表输入,一个块用于内表输入,一个块用于输出。
Cost:\(M+(⌈M/(B-2)⌉*N)\)
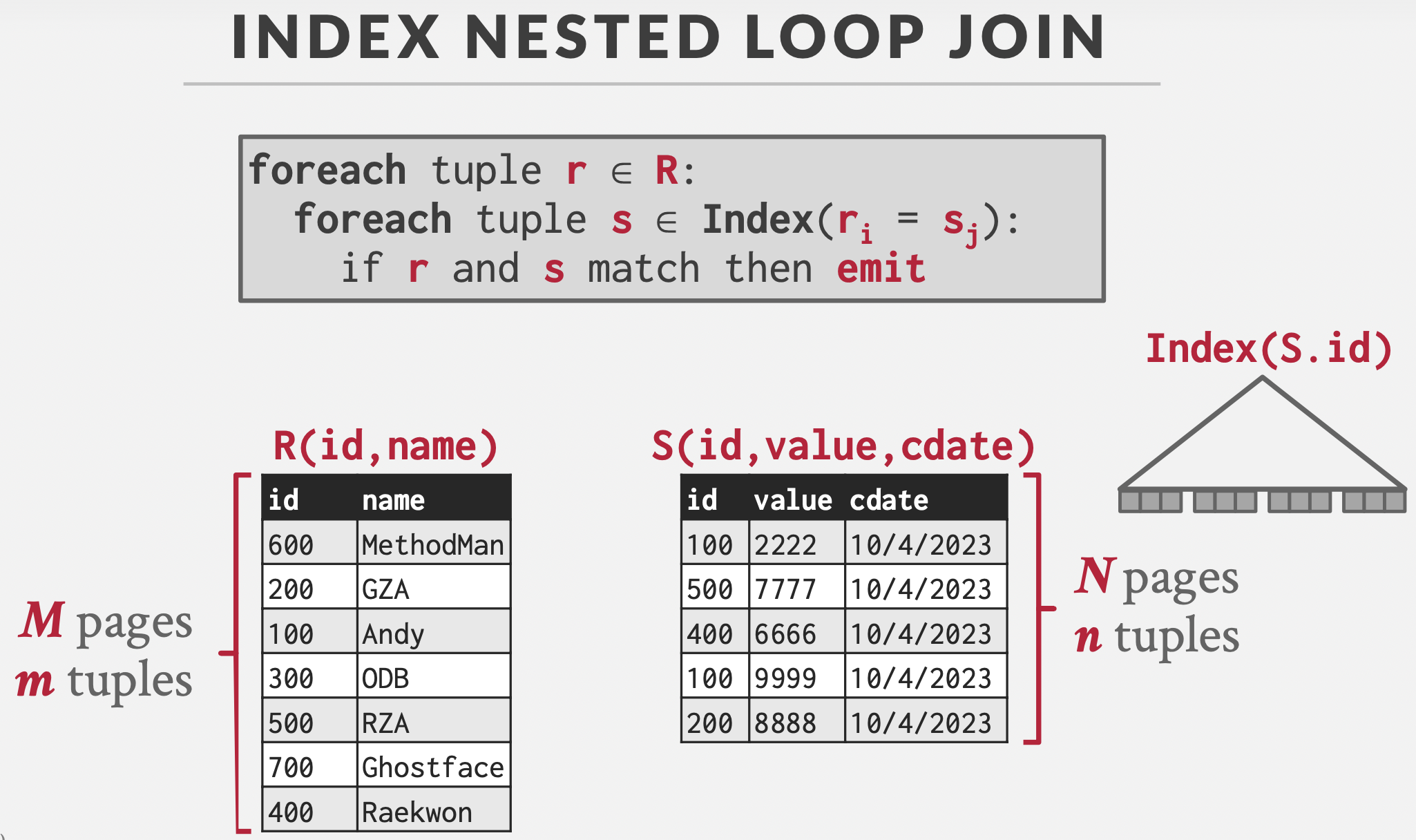
Index
前提:缓冲区大小为3,一个外表输入,一个内表输入,一个输出。
基本思想:如果外部表有索引,那么内层循环无需遍历,查询索引即可。
Cost:\(M+(m*C)\)
Sort-Merge Join
基本思想:排序后的序列更容易找到匹配项。
分为两个步骤:
- 排序:用任意排序方式,将R和S排序。
- 合并:移动两个指针寻找匹配项,过程中可能需要回退指针。
这两个步骤和上一节提到的外部归并排序思想相同,但不是同一个东西。
SortCost(R):\(2M*(1 + ⌈ log_{B-1} ⌈M / B⌉ ⌉)\)
SortCost(S):\(2N*(1 + ⌈ log_{B-1} ⌈N / B⌉ ⌉)\)
MergeCost:\(M+N\)
Total Cost:Sort + Merge
当R中存的是相同元素,且S中也是时,指针需要一直回退,Sort-Merge Join退化为Nest Loop Join。


Hash Join
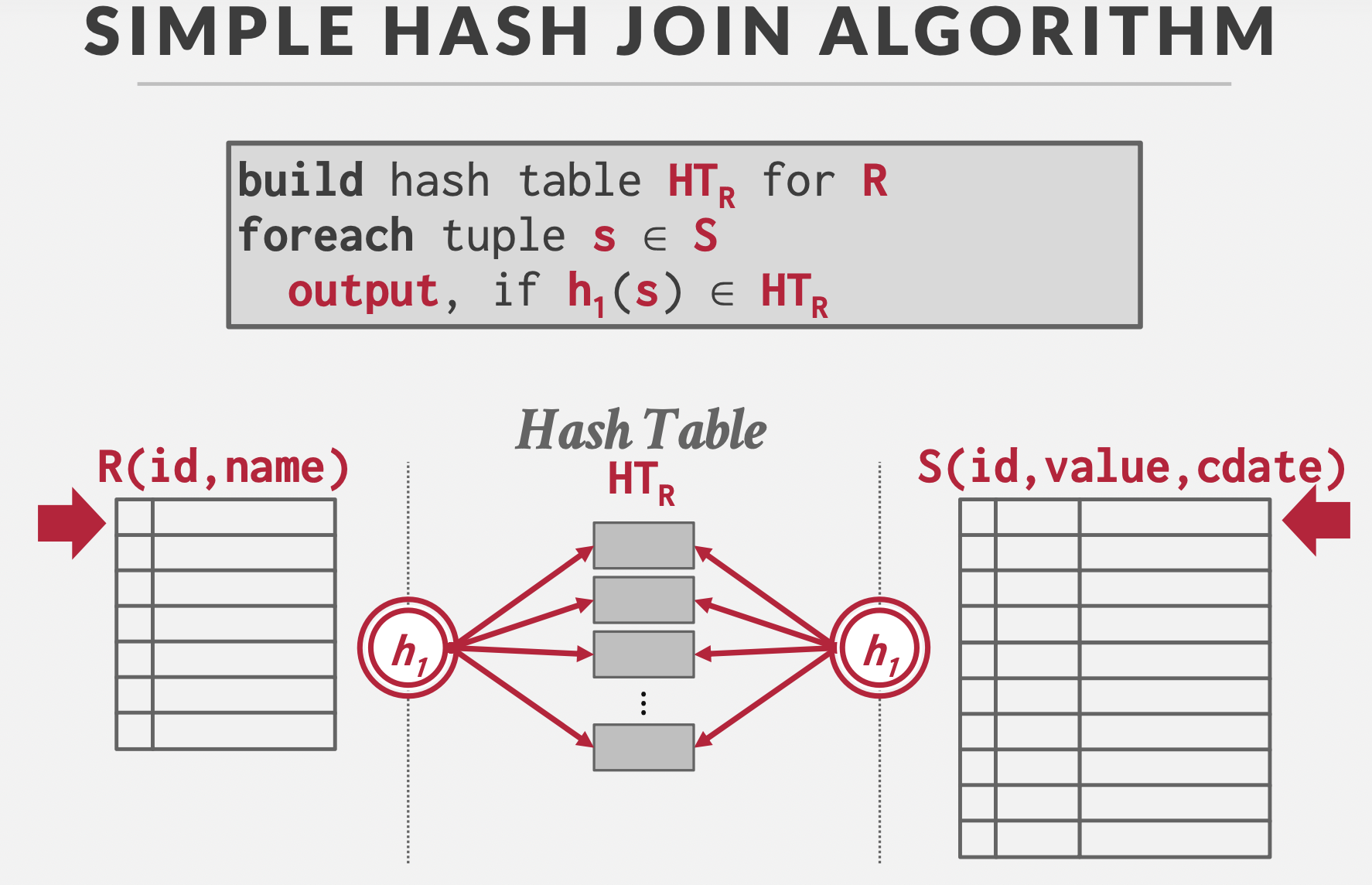
Simple Hash Join
基本思想:匹配项会被映射到同一个哈希桶。
分为两步骤:
- 构建哈希表:对R表采用哈希函数\(h_1\)进行哈希,得到哈希表,包含不同的哈希桶(可以采用不同的哈希表,但是链式哈希最符合需求)。
- 探测:把S表元组用哈希函数\(h_1\)进行哈希,得到对应的哈希桶位置,然后在哈希桶中寻找匹配项。
优化措施:布隆过滤器。
创建哈希表时顺带构建布隆过滤器,探测阶段先走布隆过滤器再走哈希桶。
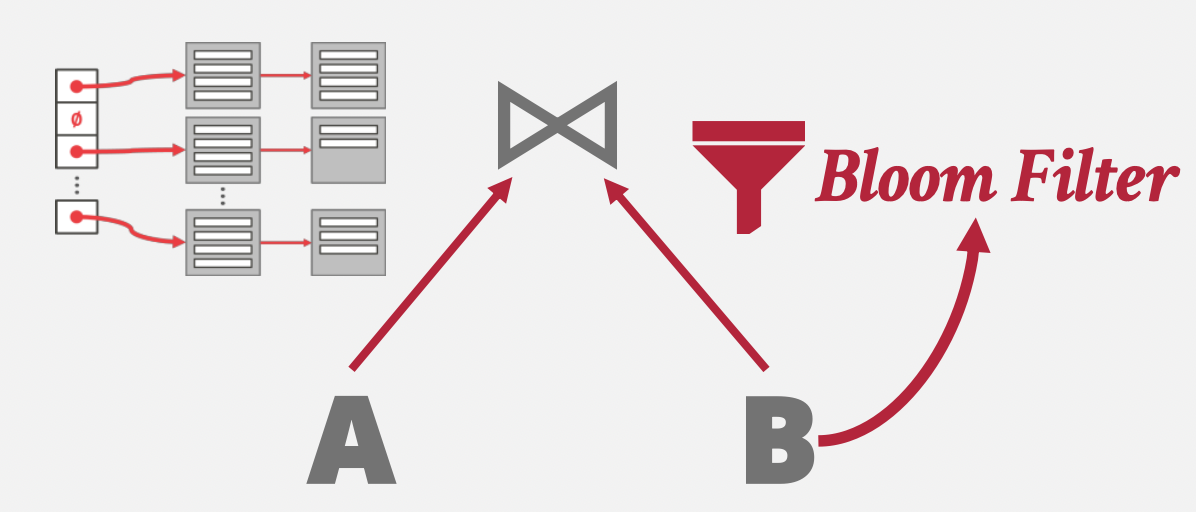
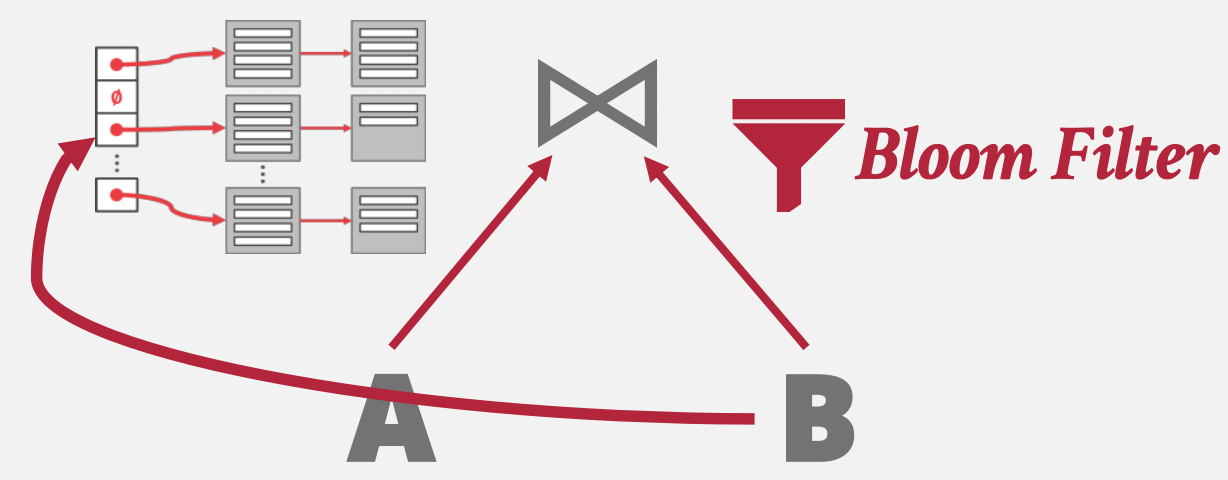
存在的问题i:该算法需要保证哈希表能存在内存中,如果哈希表太大导致无法存到内存中,需要不断地换入换出,影响效率。但不幸的是,大部分情况下,我们都不能保证内存能完全存下哈希表。
Partition Hash Join
基本思想:把两个表分别用同一个哈希函数哈希,相同哈希桶之间进行配对,如果哈希桶都存不下,就再哈希一次,直到能存下为止。
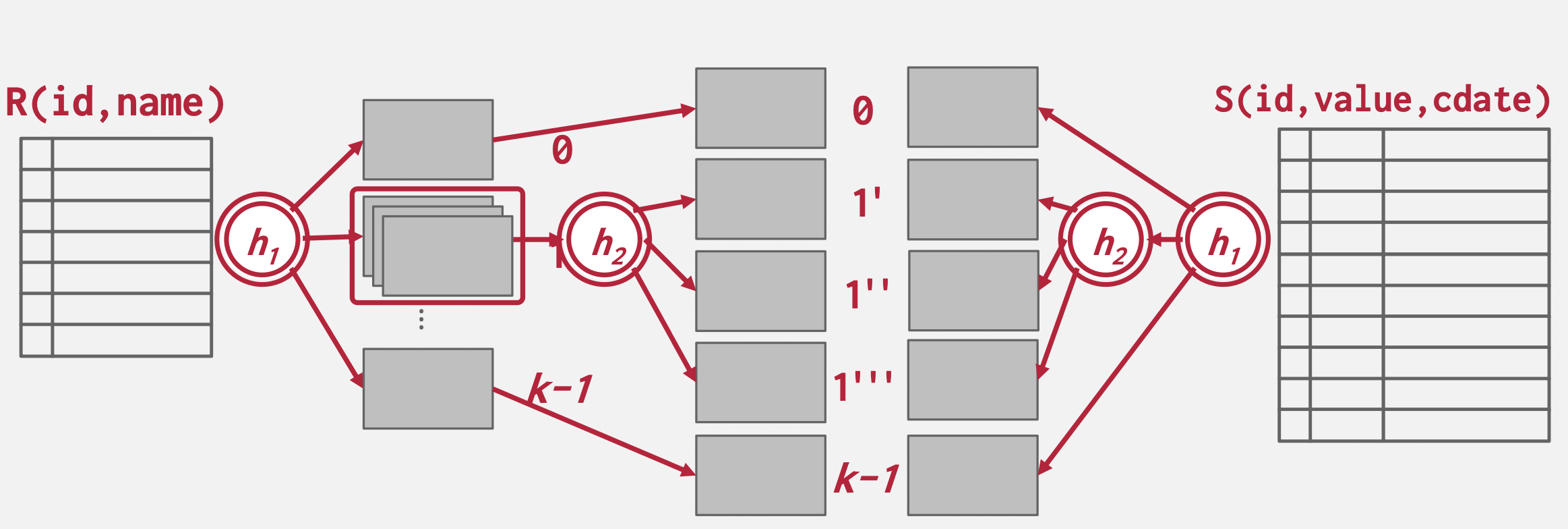
读取对应的哈希桶到内存中配对即可。
Partition Cost:\(2(M+N)\) 【读取数据+哈希桶落盘(哈希空间复杂度为\(O(n)\))】
Probe Cost:\(M+N\)
Total Cost:\(3(M+N)\)
总结
| Algorithm | IO Cost | Example |
|---|---|---|
| Naïve Nested Loop Join | \(M + (m \cdot N)\) | 1.3 hours |
| Block Nested Loop Join | $ M + (\lceil \frac{M}{B-2} \rceil \cdot N)$ | 0.55 seconds |
| Index Nested Loop Join | \(M + (m \cdot C)\) | Variable |
| Sort-Merge Join | $ M + N + (\text{sort cost})$ | 0.75 seconds |
| Hash Join | \(3 \cdot (M + N)\) | 0.45 seconds |
结论:选择Partition Hash Join,出现下述情况时使用Sort-Merge Join:
-
数据偏斜严重:Hash Join退化为Sort-Merge Join
-
数据本身需要被排序:此时Sort-Merge Join只需要额外付出 \(M+N\) 即可实现Join
一般数据库中,Hash Join和Sort-Merge Join都会实现。
标签:Sort,Join,Merge,Cost,Algorithms,cmu15545,哈希,Hash From: https://www.cnblogs.com/timothy020/p/18548006