原文链接:路径分析算法—基于Floyd算法的路径分析 – 每天进步一点点
Floyd 算法是一种用于在已知给定的加权图中求多源点之间最短路径的算法。它与Dijkstra 算法类似,不同点在于Dijkstra计算的是单源点之间的最短路径。Floyd算法是在数学建模领域和日常工作中使用频率较高的路径分析算法。
1.应用示例:任意两个城市之间的最短路径
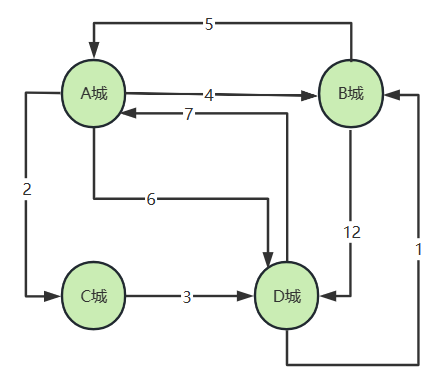
在某个旅行团举办的城际旅行活动中,计划旅行四座城市,分别是A城、B城、C城和D城,给出了如图3-2所示距离关系图,城与城的边表示城市的直接距离,城与城之间的去程距离和返程距离不一定相等,甚至可能存在只有去程没有直接返程的情况。
为了便于制定旅行计划,旅行团的导游希望在出发之前就能够了解和确定A城、B城、C城和D城中任意两个城市之间的最短距离。
2.Floyd思想
Floyed的核心思想也是基于动态规划理论,过程比较简单。
设Disti,j,k 表示为i点到j点过程中以(1…k)集合中的节点为中间节点的最短路径长度,则:
(1)若最短路径经过点k,则Disti,j,k =Disti,k,k-1 + Distk,j,k-1
(2) 若最短路径不经过点k, 则Disti,j,k = Disti,j,k-1
于是Disti,j,k=min(Disti,j,k-1 ,Disti,k,k-1+Distk,j,k-1)
Floyd算法的时间复杂度为O(n3),空间复杂度为O(n2)
3.基于Floyd算法的最短距离
根据上图给出的路径信息,我们尝试画出表格,约定同一城市的距离为0,不可直接到达的城市距离为最大值,根据城市路径信息生成的城市距离如下表:
| A城 | B城 | C城 | D城 | |
| A城 | 0 | 2 | 6 | 4 |
| B城 | 无穷大 | 0 | 3 | 无穷大 |
| C城 | 7 | 无穷大 | 0 | 1 |
| D城 | 5 | 无穷大 | 12 | 0 |
根据上表,如果要使任意两点之间的距离最短,如A城、B城两个点,则引入第三个点K城,使A城到K城的距离加上K城到B域的距离之和小于A城到B城的直接距离,则K城可能是C城或者D城,如果还有更多城市,那么K城有可能是更多城市之间的距离之和,A城到K城的距离则可以视为A城到B城最短距离的子问题。因此,存在如下确定的三种情况。
- 当任意两个城市之间不存在任何一个第三城市时,则这两个城市之间的距离则就是最短距离。
- 如果两个城市之间存在一个城市使得两个城市之间的距离最短,则它们分别到达该中间城市的距离应当是最短距离,即依赖于第一种情况。
- 如果两个城市之间存在两个或者多个城市时,那么它可以拆分两个或者多个第二种情况的问题。
基于上述判定,解决步骤如下。
(1)确定当两个城市之间不存在任何一个第三城市时,城市之间的最短距离表如下:
| A | B | C | D | |
| A | 0 | 2 | 6 | 4 |
| B | 无穷大 | 0 | 3 | 无穷大 |
| C | 7 | 无穷大 | 0 | 1 |
| D | 5 | 无穷大 | 12 | 0 |
(2)求只允许通过A城作为中间城市后的城市最短距离如下表,其中,带下划线的数值表示更新后的城市之间的最短距离.
| A | B | C | D | |
| A | 0 | 2 | 6 | 4 |
| B | 无穷大 | 0 | 3 | 无穷大 |
| C | 7 | 9 | 0 | 1 |
| D | 5 | 7 | 11 | 0 |
(3)在上述的基础上,继续求通过A城以及B城作为中间城市后的最短距离如下:
| A | B | C | D | |
| A | 0 | 2 | 5 | 4 |
| B | 无穷大 | 0 | 3 | 无穷大 |
| C | 7 | 9 | 0 | 1 |
| D | 5 | 7 | 10 | 0 |
(4)同理,计算求通过A城,B城,C城作为中转城市后的最短距离如下:
| A | B | C | D | |
| A | 0 | 2 | 5 | 4 |
| B | 10 | 0 | 3 | 4 |
| C | 7 | 无穷大 | 0 | 1 |
| D | 5 | 无穷大 | 10 | 0 |
(5)最后将所有城市都视为中间城市,则任意两个城市之间的最短路径如下:
| A | B | C | D | |
| A | 0 | 2 | 5 | 4 |
| B | 9 | 0 | 3 | 4 |
| C | 6 | 8 | 0 | 1 |
| D | 5 | 7 | 10 | 0 |
上述过程的流程是当最开始只允许经过A城市作为中间城市的最短路径,然后依次A城和B城同时作为中间城市时,是一种典型的动态规划思想,最终求得上表即为最终的任意两个城市之间的最短距离.
标签:无穷大,路径分析,城市,距离,算法,Floyd,短距离 From: https://www.cnblogs.com/longkui-site/p/18532213