\(Manacher\) 算法

\(Manacher(马拉车)\) 算法，是一种高效解决最长回文子串问题的算法。其 \(O(n)\) 的复杂度相较于暴力 \(O(n^2)\) 和字符串哈希 \(O(nlogn)\) 来说，快了不少。

算法实现：

首先说一下暴力的解法，对于每一个字符串上的字符，考虑以其为起点，向两边扩展。若字符串上回文串不多且长度普遍较短，则暴力的时间复杂度接近 \(O(n)\) 。当然，若其回文串数量较多且长度较长时，暴力的复杂度将退化成 \(O(n^2)\) 。

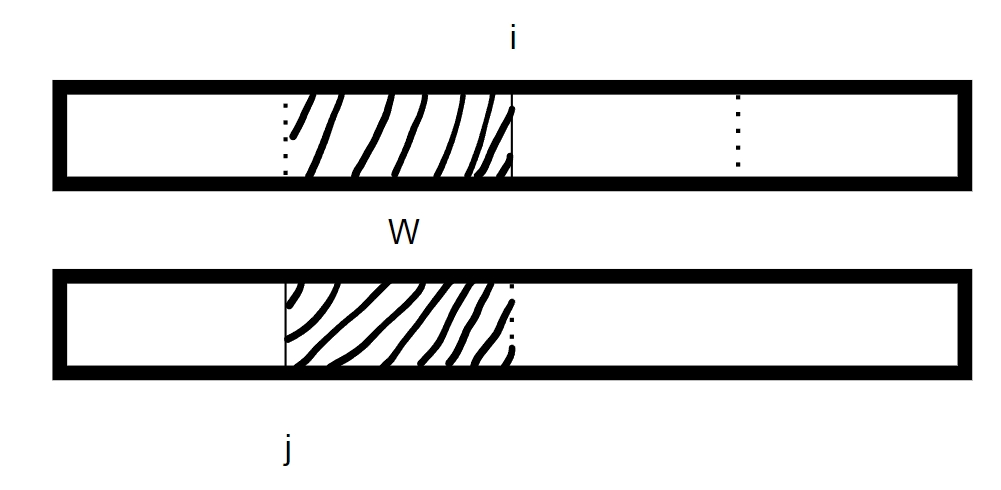
如上图，在计算以 \(i\) 和以 \(j\) 为中心的回文字符串时，重复计算了一段 \(w\) 区间，这也是暴力的效率低的原因，考虑对其进行优化。应该优化掉这种重复计算。

首先，同一其形式，由于回文字符串分为奇数长度的和偶数长度的，其中心也有所不同，所以先将待处理的字符串进行一个小处理。在开头和结尾处加上两个不同的字符，防止越界，在其中的每个字符中，加入其中不会出现的字符来分割每个字符。这样使的两种不同的字符串都会变为奇数字符串。

例：由 \(ABBA\) 变为 \(\$A\#B\#B\#A\&\) ，则其中心字符由 \(BB\) 变为 \(\#\) 省去了分类讨论，同时可证得这样初始化字符串并不会改变其的回文性质，即原先回文的子串在初始化后仍是回文的。

然后是对回文子串长度的统计，设 \(p[i]\) 表示以 \(i\) 为中心的回文串的半径，当然，我们还需要了解另一个重要的性质：回文的镜像也是回文，概括一下说的话大概是：对于一个回文字符串 \(s\) 来说，其中心字符左右两侧的回文字符串在另一侧必定会有一个相同的回文子串 ，我们可以利用这个性质，对于 \(p[i]\) 来说，已知 \(p[1],p[2],p[3]...p[i-1]\) ，令 \(R\) 为这之前的回文字符串的最右端点，\(C\) 是 \(R\) 所在的回文字符串的中心字符，即 \(p[C]\) 是一个已经求过的点， \(R\) 是其右端点且是已经求得的所有右端点中最大的， \(R=C+p[C]\) 。对于 \(R\) 左边的回文串来说，可以利用性质减少暴力的次数，从而优化程序。

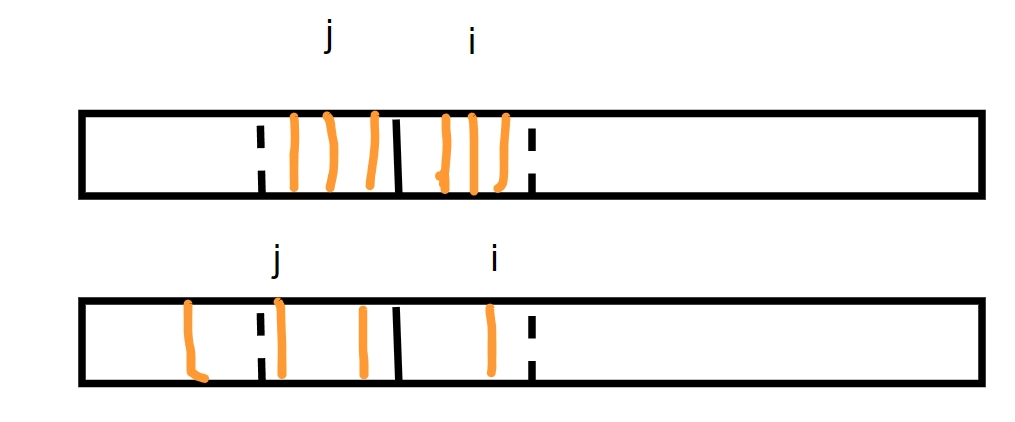
当有节点 \(i<R\) 时，其分为两种情况(PS： \(j\) 为 \(i\) 关于 \(C\) 对称的回文子串)，如下图：

1.若 \(j\) 的区间左端点大于区间 \(C\) 的左端点，即图上第一种情况，即 \(j \subseteq C\) ，那么由于 \((i+j)/2=C\) (中点坐标公式)，可得 \(j=C \times 2-i\) 则 \(p[i]=p[C \times 2-i]\) ，后再用暴力扩展法扩展(由于不知道是否到达最长)。

2.若 \(j\) 的区间左端点小于区间 \(C\) 的左端点，即图上第二种情况，即 \(j \nsubseteq C\) ，由于性质条件不成立，则只能投影一部分，则可以被投影的区间为 \(p[i]=w=R-i=p[C]+C-i\) ，后再用暴力扩展法向后推。

这两种情况可以统一处理，取最小值，后再用暴力向外扩展即可。

当然，不可能全部都在其左边，当有节点 \(i \geqslant R\) 时，由于还没有计算到，则只能令 \(p[i]=1\) 后向后暴力扩展求 \(q[i]\) 。

我们会发现无论是那种情况，最后还是要回到暴力扩展法上，不禁担心其复杂度的正确性，关于其证明，后面再给出。

code

char s[maxn];          //要处理的字符串
char s1[maxn];         //初始化后的字符串
int n,ans;             //字符串长度,答案
void in_it(){
	int k=0;
    s1[k++]='$';       //开头 
    s1[k++]='#';
    for(int i=0;i<n;i++){
        s1[k++]=s[i];
        s1[k++]='#';
	}
    s1[k++]='&';      //结尾
    n=k;              //更新字符串长度
}
void manacher(){
    int r=0,c;        //初始化最右点，
    for(int i=1;i<n;i++){
        //分类讨论
        if(i<r) p[i]=min(p[(c<<1)-i],p[c]+c-i);
        else    p[i]=1;
        //暴力向两边扩展
        while(s1[i+p[i]]==s1[i-p[i]]) p[i]++;
        if(p[i]+i>r){     //若超出最右点
            c=i;
            r=p[i]+i;     //更新
        }
    }
}
signed main(){
	cin>>s;
    n=strlen(s);
    in_it();
    manacher();
    for(int i=0;i<n;i++){
        ans=max(ans,p[i]); //更新ans
    }
	cout<<ans-1;
}

在看完代码后，我们发现其实执行 \(manacher\) 函数的过程其实是不断计算 \(p[i]\) ，实际是向右推进 \(R\) 的过程。由于 \(R\) 不会重复遍历，所以其复杂度为 \(O(n)\) 。