优化算法（四）—蚁群算法（附MATLAB程序）

标签：numCities 蚁群路径信息 ant 算法 MATLAB end 蚂蚁

蚁群算法（Ant Colony Optimization, ACO）是一种模拟蚂蚁觅食行为的优化算法，由Marco Dorigo于1990年提出。它利用了蚂蚁在寻找食物的过程中通过释放信息素来相互影响的机制，以找到最优解或接近最优解。蚁群算法特别适用于解决组合优化问题，如旅行商问题（TSP）、调度问题等。

一、基本原理

蚁群算法（Ant Colony Optimization, ACO）是一种基于自然界蚂蚁觅食行为的启发式优化算法，主要用于解决组合优化问题。其基本原理包括以下几个关键点：

1. 信息素的作用：
- 蚂蚁在寻找食物的过程中，会在所经过的路径上释放信息素。信息素的浓度表示路径的优劣，浓度越高，路径越受蚂蚁欢迎。

2. 随机选择：
- 蚂蚁在选择路径时，除了考虑信息素浓度外，还会引入随机性，以增加探索新路径的机会。这种随机性有助于避免早期收敛到局部最优解。

3. 信息素更新机制：
- 每次迭代后，信息素会根据蚂蚁选择的路径进行更新。表现良好的路径会增加信息素浓度，而不佳的路径信息素会逐渐挥发。这一机制确保了优秀路径的持续吸引力。

4. 迭代过程：
- 蚂蚁会在多个迭代中不断探索和更新路径信息，通过不断的迭代，逐渐找到最优或近似最优解。

5. 适用性：
- 蚁群算法可以广泛应用于旅行商问题、网络路由、调度问题、图像处理等多个领域，适合于处理复杂的组合优化问题。

总结来说，蚁群算法通过模拟蚂蚁觅食的行为，利用信息素引导搜索，结合随机性和迭代机制，有效地解决复杂的优化问题。

二、公式推导

蚁群算法的核心在于信息素的更新和蚂蚁路径选择的概率计算。以下是一些基本公式及其推导过程：

2.1信息素更新公式

信息素的更新通常分为两个部分：挥发和增强。

挥发：在每次迭代后，所有路径的信息素会以一定的速率挥发。这个过程通常用以下公式表示：

其中：

$\tau _{ij}\left ( t \right )$ 是在时间 $t$ 时刻边 $ij$ 上的信息素浓度。
$\rho$ 是挥发系数（ $0< \rho < 1$ ）。

增强：经过一轮蚂蚁的搜索后，优秀路径上的信息素会增加，通常用以下公式表示：

其中， $\Delta \tau _{ij}$ 是在路径 $ij$ 上增加的信息素，通常由路径的质量（如路径长度）决定：

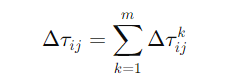
其中 m是当前迭代中使用该路径的蚂蚁数量， $\Delta \tau^{k} _{ij}$ 可以表示为：

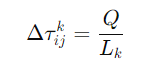
其中：

Q 是常数（信息素强度）。
$L_{k}$ 是蚂蚁 k 经过的路径长度。

2.2路径选择概率公式

蚂蚁在选择下一个路径时，会基于信息素浓度和启发式信息（如距离）来决定。选择概率可以表示为：

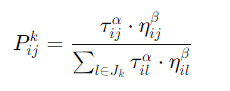
其中：

$P_{ij}^{k}$ 是蚂蚁 k从节点 i选择节点 j的概率。
$\tau _{ij}$ 是边 $ij$ 上的信息素浓度。
$\eta _{ij}$ 是启发式信息（通常为 $1/d_{ij}$ ，即边的倒数距离）。
$J_{k}$ 是蚂蚁 k 可选择的邻接节点集合。
α 和 β是调节参数，分别控制信息素和启发式信息的影响程度。

2.3迭代过程

通过上述信息素更新和路径选择的迭代，蚁群算法不断优化路径，逐渐趋向最优解。

三、MATLAB仿真

以下是一个简单的蚁群算法（ACO）在MATLAB中的仿真示例，主要用于解决旅行商问题（TSP）。该代码框架包含了蚁群算法的基本组成部分。

function ant_colony_optimization_tsp()
    % 城市坐标
    cities = [0, 0; 1, 2; 2, 1; 3, 3; 4, 0]; % 示例城市坐标
    numCities = size(cities, 1);
    
    % 参数设置
    numAnts = 10;          % 蚂蚁数量
    numIterations = 100;   % 迭代次数
    alpha = 1;             % 信息素重要程度
    beta = 2;              % 启发式信息重要程度
    rho = 0.1;             % 信息素挥发率
    Q = 100;               % 信息素常数

    % 初始化信息素和距离矩阵
    tau = ones(numCities, numCities); % 信息素矩阵
    distances = zeros(numCities, numCities); % 距离矩阵

    for i = 1:numCities
        for j = 1:numCities
            distances(i, j) = norm(cities(i, :) - cities(j, :));
        end
    end

    bestLength = inf;
    bestPath = [];

    % 主循环
    for iteration = 1:numIterations
        paths = zeros(numAnts, numCities);
        lengths = zeros(numAnts, 1);
        
        % 蚂蚁循环
        for ant = 1:numAnts
            % 初始化蚂蚁路径
            visited = false(numCities, 1);
            startCity = randi(numCities);
            currentCity = startCity;
            visited(currentCity) = true;
            paths(ant, 1) = currentCity;

            for step = 2:numCities
                % 计算下一城市选择概率
                probabilities = calculateProbabilities(currentCity, visited, tau, distances, alpha, beta);
                nextCity = rouletteWheelSelection(probabilities);
                
                % 更新路径和当前城市
                paths(ant, step) = nextCity;
                visited(nextCity) = true;
                currentCity = nextCity;
            end
            
            % 计算路径长度
            lengths(ant) = calculatePathLength(paths(ant, :), distances);
            
            % 更新最佳路径
            if lengths(ant) < bestLength
                bestLength = lengths(ant);
                bestPath = paths(ant, :);
            end
        end

        % 信息素更新
        tau = (1 - rho) * tau; % 挥发
        for ant = 1:numAnts
            for step = 1:numCities-1
                i = paths(ant, step);
                j = paths(ant, step + 1);
                tau(i, j) = tau(i, j) + Q / lengths(ant);
            end
            % 最后返回到起点
            i = paths(ant, numCities);
            j = paths(ant, 1);
            tau(i, j) = tau(i, j) + Q / lengths(ant);
        end
    end
    
    % 输出最佳路径和长度
    fprintf('最佳路径: %s\n', num2str(bestPath));
    fprintf('最佳路径长度: %.2f\n', bestLength);
end

function probabilities = calculateProbabilities(currentCity, visited, tau, distances, alpha, beta)
    numCities = length(visited);
    probabilities = zeros(numCities, 1);
    
    for j = 1:numCities
        if ~visited(j)
            probabilities(j) = (tau(currentCity, j) ^ alpha) * ((1 / distances(currentCity, j)) ^ beta);
        end
    end
    
    probabilities = probabilities / sum(probabilities);
end

function nextCity = rouletteWheelSelection(probabilities)
    cumulativeProbabilities = cumsum(probabilities);
    randomValue = rand();
    nextCity = find(cumulativeProbabilities >= randomValue, 1);
end

function length = calculatePathLength(path, distances)
    length = 0;
    for i = 1:length(path)-1
        length = length + distances(path(i), path(i+1));
    end
    % 返回起点
    length = length + distances(path(end), path(1));
end

代码解释

城市坐标：cities变量定义了城市的坐标。
参数设置：设置了蚂蚁数量、迭代次数、信息素和启发式信息的重要性等参数。
信息素和距离矩阵：初始化信息素矩阵和城市之间的距离矩阵。
主循环：通过多次迭代让蚂蚁找到路径，并更新信息素。
路径选择和更新：使用轮盘赌选择下一城市，并在每轮结束后更新信息素。

使用方法

将上述代码复制到MATLAB的脚本文件中，运行ant_colony_optimization_tsp函数，即可查看结果。

此示例是一个基础版本，您可以根据需要进一步优化和调整参数，或增加更多功能（如图形可视化等）。

四、总结

蚁群算法通过信息素的动态更新和基于概率的路径选择，模拟自然界中蚂蚁的觅食行为，解决复杂的组合优化问题。以上公式是该算法的基本框架，具体应用时可能会根据问题的特点进行调整。

优化算法以往链接：

优化算法（一）—遗传算法（Genetic Algorithm）附MATLAB程序-CSDN博客

优化算法（二）—粒子群优化算法（附MATLAB程序）-CSDN博客

优化算法（三）—模拟退火算法（附MATLAB程序）_模拟退火算法csdn-CSDN博客

标签：numCities,蚁群,路径,信息,ant,算法,MATLAB,end,蚂蚁
From： https://blog.csdn.net/qq_35623594/article/details/142187627