从某一个顶点开始构建生成树,每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。
时间复杂度:O(|V|*|V|),适合用于边稠密图。
普里姆算法构建最小生成树的过程
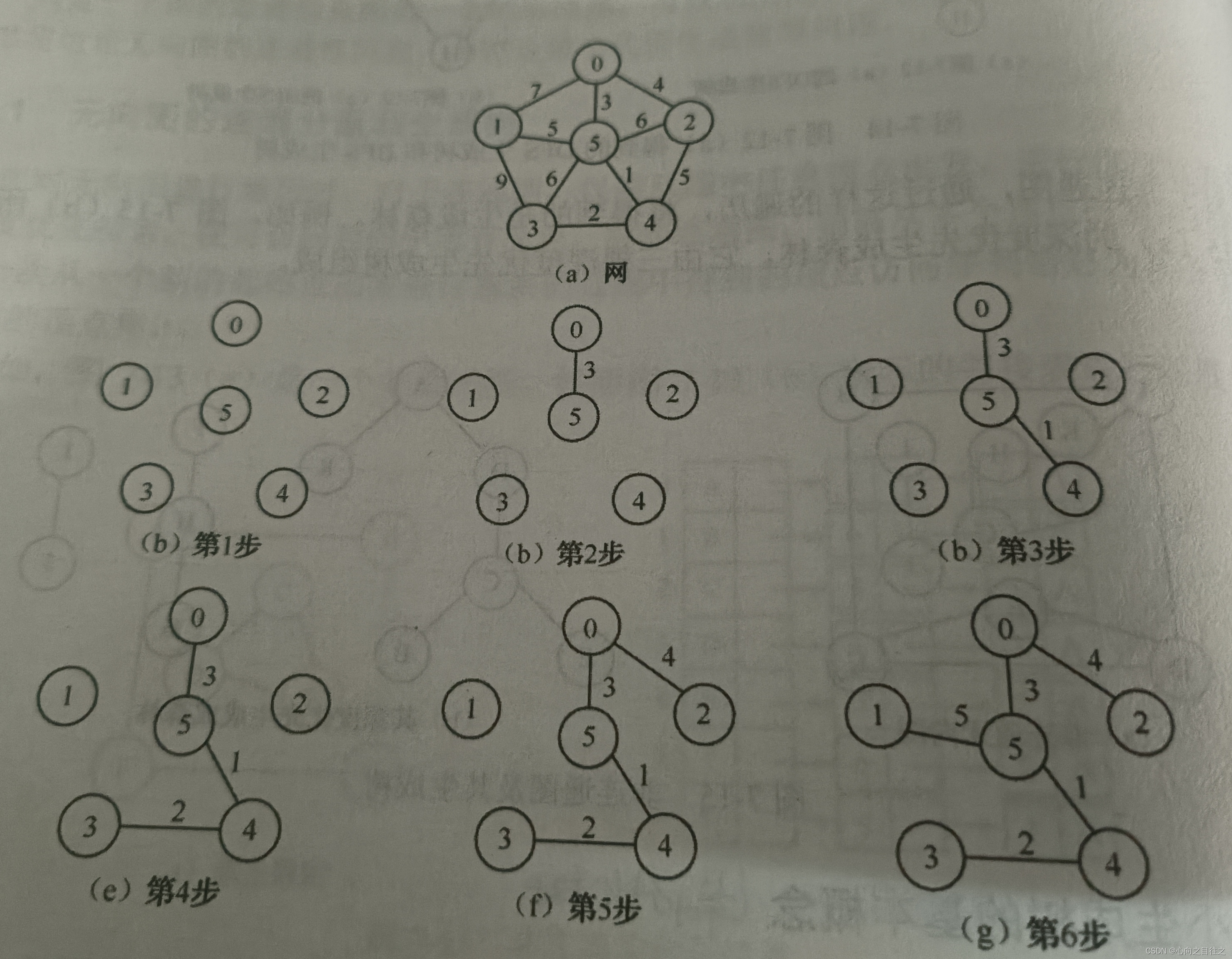
用Prim算法构造如下图所示连通图最小生成树过程中参数的变量示意
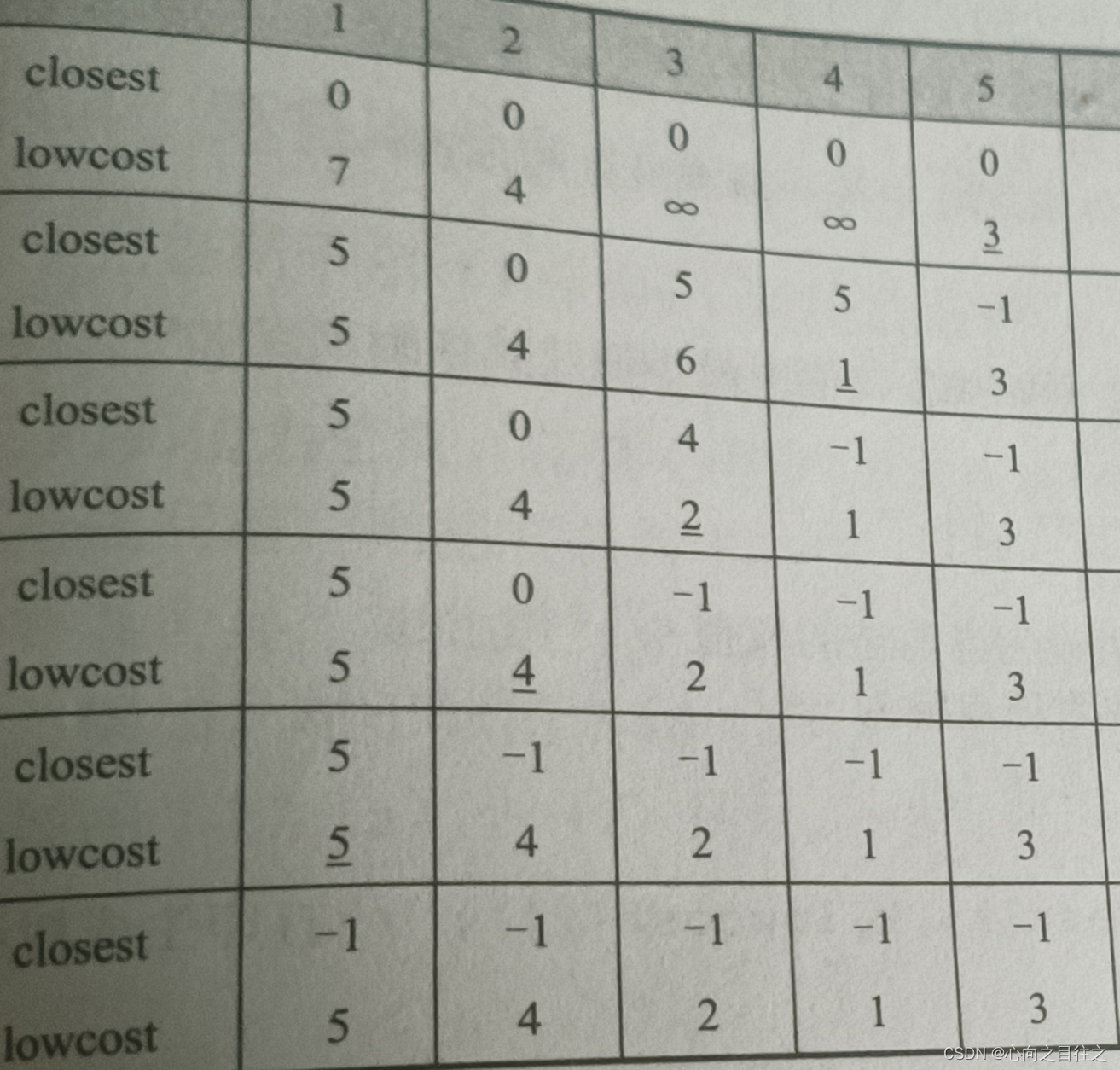
实现Prim算法的完整代码如下
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#define MAX 100//图中最大顶点个数
#define M 32767 //无穷大
//生成无向网的邻接矩阵算法
int Creatcost(int cost[][MAX]) {
printf("\n请输入顶点数和边数:");
int vnum, anum;
scanf("%d%d", &vnum, &anum);
int i = 0, j = 0;
for (i = 0; i < vnum; i++)
for (j = 0; j < vnum; j++)
cost[i][j] = M;//预设矩阵中各值为最大值
printf("请输入各边及权值(顶点序号从1开始):\n");
int k = 0;
int v1, v2, w;//顶点v1,顶点v2,权值w
for (k = 0; k < anum; k++) {
printf("v1 v2 w:");
scanf("%d%d%d", &v1, &v2, &w);//输入各顶点及权值
cost[v1][v2] = w;//将(v1,v2)的权值为w
cost[v2][v1] = w;//无向图中将(v1,v2)的权值为w
}
return vnum;//返回顶点数
}
//已知图的顶点为{0,1,...,n-1},c[i][j]为边(i,j)的权,
//打印最小生成树的每条边
void Prim(int c[MAX][MAX], int n) {
int i = 0,lowcost[MAX],closet[MAX];
for (i = 1; i < n; i++) {
lowcost[i] = c[0][i];//将lowcost数组中各元素设为从顶点0到各顶点的权值
closet[i] = 0;//依附于该边的顶点为0
}
closet[0] = -1;//置初值为-1
int min, k,j;
for (i = 1; i < n; i++) {//求某一顶点最近的顶点
min = M;//最小值初始无穷大
k = i;
for (j = 0; j < n; j++) {//从顶点1开始找各权值中最小值及其依附顶点k
if (lowcost[j] < min && closet[j] != -1) {
min = lowcost[j];//最小值设为当前的权值
k = j;//此边依附顶点赋为j
}
}
printf("(%d,%d) 权值%d\n", closet[k], k, lowcost[k]);//打印
closet[k] = -1;
for (j = 1; j < n; j++) {//设顶点k为下次查找的起始点
if (closet[j] != -1 && c[k][j] < lowcost[j]) {
lowcost[j] = c[k][j];
closet[j] = k;
}
}
}
}
int main() {
int n;//图中顶点个数
int cost[MAX][MAX];//邻接矩阵数组
n=Creatcost(cost);//调用建立邻接矩阵数组函数
printf("\n最小生成树:\n");
Prim(cost, n);//调用普里姆算法
return 0;
}
运行结果入下:
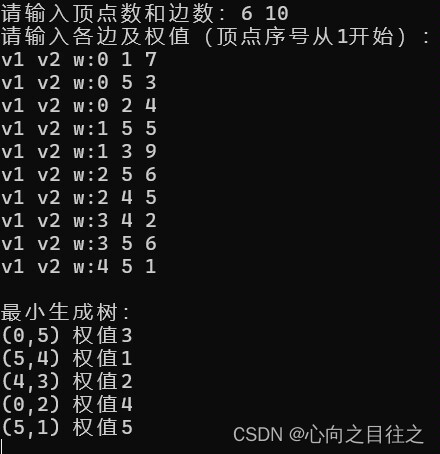
标签:普里,closet,int,MAX,v2,算法,lowcost,顶点,Prim From: https://blog.csdn.net/2302_76311249/article/details/141896713