算法·理论：KMP 笔记

\(\text{KMP}\) 笔记！

上次比赛，出题人出了一个 \(\text{KMP}\) 模板，我敲了个 \(\text{SAM}\) 跑了，但是学长给的好题中又有很多 \(\text{KMP}\)，于是滚回来恶补字符串基本算法。

\(\text{KMP}\) 是上个寒假学的，为什么最近才完全理解，但 \(\text{KMP}\) 短小精悍，极其精简，确实难懂，所以很长一段时间都躲着它，最近突发灵感，遂写此篇。

前置知识：字符串基础，字符串匹配（基本概念）

引入

\(\text{KMP}\) 算法，用于解决字符串匹配问题。这一类问题一般可以表述为「在主串 \(S\) 中查找模式串 \(T\) 的某些信息」。

显然我们有一种十分暴力的算法：枚举模式串 \(T\) 的起点，往后一位一位的比较。记 \(S\) 的长度为 \(n\)，\(T\) 的长度为 \(m\)，显然这种算法最坏是 \(O(nm)\) 的。

给出这种暴力的实现：

// force.cpp
int n,m;
char s[N],t[M];
void force(){
	for(int st=1;st+m-1<=n;st++){
		int i=st,j=1;
		while(j<=m&&s[i]==t[j]) i++,j++;
		if(j>m){
			// do something
		}
	}
}

当然我们可以用字符串哈希做到 \(O(n+m)\) 预处理，\(O(1)\) 比较两个字符串，复杂度变成 \(O(n+m)\)。实际上，这也是 \(\text{KMP}\) 的复杂度，但是 \(\text{KMP}\) 可以做到更多。

前缀函数-定义与性质

定义一个字符串 \(s\) 的前缀函数 \(nxt[i]\) 为 \(s\) 长度为 \(i\) 的前缀 \(s[1\colon i]\) 的最长公共真前后缀的长度，为了方便用数组形式表式。

晕？不慌，看个例子。

比如说 \(s=\texttt{abcab}\)，容易发现，\(\texttt{ab}\) 既是 \(s\) 的真前缀，又是 \(s\) 的真后缀，所以它是 \(s\) 的公共真前后缀，又发现 \(s\) 仅有 \(\texttt{ab}\) 一个公共真前后缀，所以 \(\texttt{ab}\) 自然是最长公共真前后缀，所以 \(s\) 的最长公共真前后缀的长度就等于 \(2\)。

接下来，你能写出 \(\texttt{ababc}\) 的 \(nxt[]\) 吗？

• 对于 \(nxt[1]\)，对应的前缀是 \(\texttt{a}\)，最长公共真前后缀为空串（真前/后缀不算本身），于是 \(nxt[1]=0\)。
• 对于 \(nxt[2]\)，对应的前缀是 \(\texttt{ab}\)，最长公共真前后缀为空串，于是 \(nxt[2]=0\)。
• 对于 \(nxt[3]\)，对应的前缀是 \(\texttt{aba}\)，最长公共真前后缀为 \(\texttt{a}\)，于是 \(nxt[3]=1\)。
• 对于 \(nxt[4]\)，对应的前缀是 \(\texttt{abab}\)，最长公共真前后缀为 \(\texttt{ab}\)，于是 \(nxt[4]=2\)。
• 对于 \(nxt[5]\)，对应的前缀是 \(\texttt{ababc}\)，最长公共真前后缀为空串，于是 \(nxt[5]=0\)。

综上，\(\texttt{ababc}\) 的 \(nxt[]\) 为 \(\{0,0,1,2,0\}\)。

再来讲两个 \(nxt[]\) 数组的性质：

• 性质 \(\bf{1}\)：\(nxt[i]<i\)，由定义得到。
• 性质 \(\bf{2}\)：设字符串 \(s\)，\(p=\lvert s \rvert\)，不断去做 \(p=nxt[p]\)，出来的每个值即为原串的每个公共真前后缀的长度。（包括 \(nxt[p]\)、\(nxt[nxt[p]]\)、\(nxt[nxt[nxt[p]]]\)……）

性质 \(\bf{2}\) 证明

拿前两次来说，初始的 \(nxt[p]\) 是原串的每最长公共真前后缀的长度，所以 \(nxt[nxt[i]]\) 即为长度为 \(nxt[p]\) 的前缀的最长公共真前后缀的长度，记这个最长公共真前后缀为 \(u\)，那么原串就有前缀 \(u\)。

但又因为长度为 \(nxt[p]\) 的前缀等于长度为 \(nxt[p]\) 的后缀，所以长度为 \(nxt[p]\) 的后缀也有长度为 \(nxt[nxt[p]]\) 的最长公共真前后缀 \(u\)，那么原串就也有后缀 \(u\)。所以原串有公共真前后缀 \(u\)。

于是继续这样递归的理解一下，这样嵌套下去，每个值显然都是原串的公共真前后缀（把空串也理解为公共真前后缀）。

\(\bf{KMP}\)-匹配过程

想想怎么优化我们前文讲的 \(O(nm)\) 暴力。

比如说 \(S=\texttt{abababc}\)，\(T=\texttt{ababc}\)：

\(\texttt{\color{grey}{abababc}}\)
\(\texttt{\color{grey}{ababc}}\)

一开始，显然前四位都能匹配上：

\(\texttt{\color{green}{abab}\color{grey}{abc}}\)
\(\texttt{\color{green}{abab}\color{grey}{c}}\)

但到第五位，字符不同，这时我们称发生了一次失配：

\(\texttt{\color{green}{abab}\color{red}{a}\color{grey}{bc}}\)
\(\texttt{\color{green}{abab}\color{red}{c}}\)

正常暴力时，我们需要将模式串往右移一位，全部重新匹配，像这样：

\(\texttt{\color{grey}{abababc}}\)
\(\texttt{ \color{grey}{ababc}}\)

然后继续比较：

\(\texttt{\color{grey}{a}\color{red}{b}\color{grey}{ababc}}\)
\(\texttt{ \color{red}{a}\color{grey}{babc}}\)

但是，显然有一种更加聪明的办法，由于模式串 \(T\) 已经匹配好了一段前缀 \(\texttt{abab}\)，并且这段前缀中存在两段一样的字符 \(\texttt{ab|ab}\)，所以后面一段 \(\texttt{ab}\) 匹配好的 \(S\) 的第三第四位可以直接给 \(T\) 的第一第二为用，并且直接从 \(T\) 的第三位为开始比较：

\(\texttt{\color{grey}{ab}\color{green}{ab}\color{grey}{abc}}\)
\(\texttt{\color{white}{--}\color{green}{ab}\color{grey}{abc}}\)

接着向后比较，匹配成功：

\(\texttt{\color{grey}{ab}\color{green}{ababc}}\)
\(\texttt{\color{white}{--}\color{green}{ababc}}\)

懂了又好像没懂？总而言之，我们的基本思想就是利用已经匹配了的部分和模式串 \(T\) 本身相同的部分进行优化。

已经匹配了的部分简单，但是现在问题就来了：什么样的 \(T\) 的相同部分可以被利用呢？怎么跳转呢？

先说结论：设当前 \(S[i+1] \neq T[j+1]\)，即 \(S\) 和 \(T\) 即将失配，那么接下来的最小可能匹配位置为 \(i-nxt[j]+1\)（\(T\) 的开头位置），同时不需要移动 \(i\)，直接 \(j\leftarrow nxt[j]\)，然后继续比较 \(S[i+1] \neq T[j+1]\) 即可。

比如在上面的例子中，\(\texttt{ababc}\) 的匹配到 \(S[4]=T[4]\)，但是在下一位 \(S[5] \neq T[5]\)，也就是要失配了，所以我们 \(j\leftarrow nxt[j]\) 即 \(j\leftarrow nxt[4]\) 即 \(j\leftarrow 2\)，于是继续比较 \(S[5]\) 和 \(T[3]\) 即可。

证明

首先 \(i-nxt[i]+1\) 的正确性显然，就是利用 \(nxt[i]\) 提供的前后相等的信息，直接完成前 \(nxt[i]\) 位的匹配。

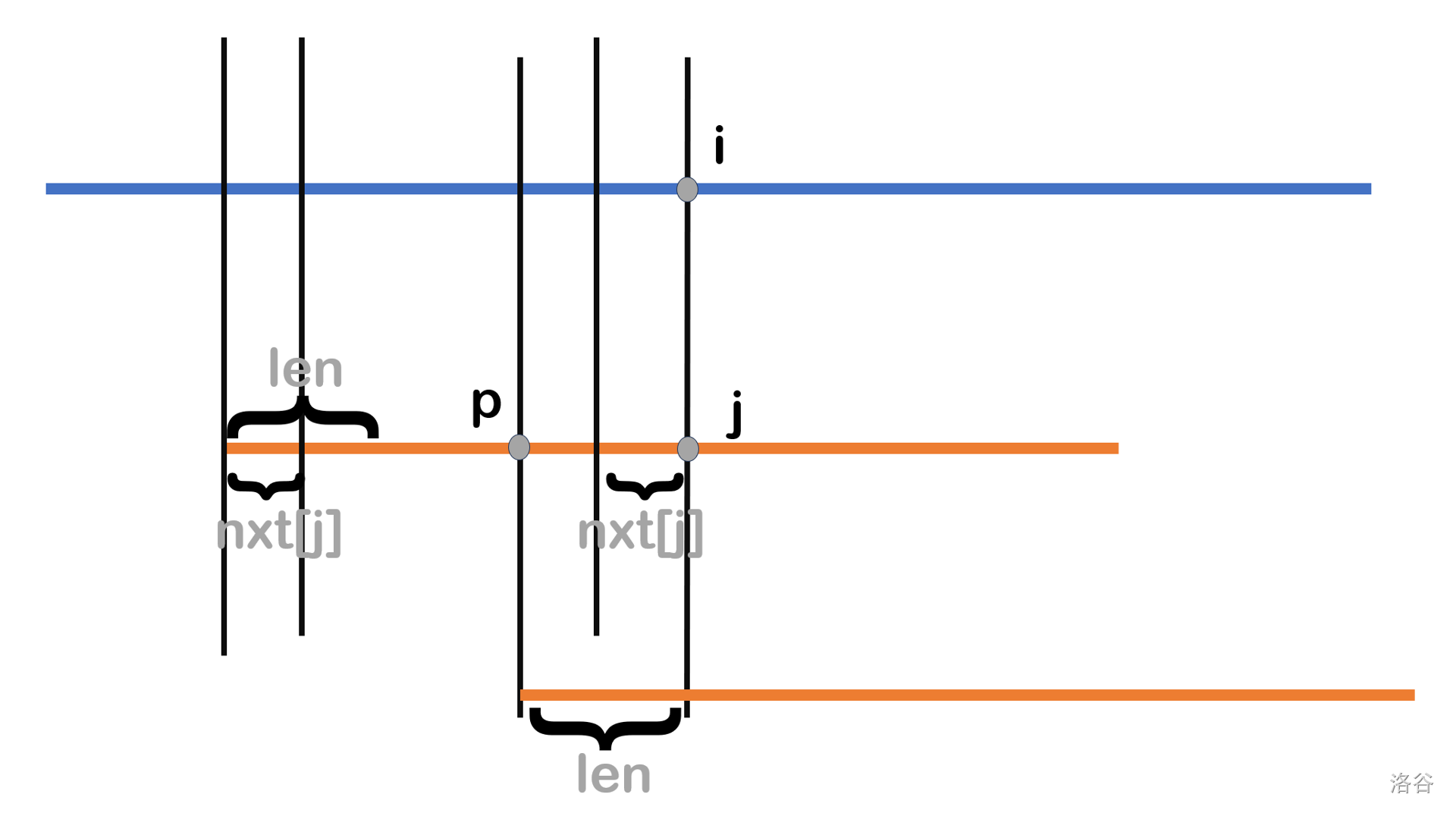
接着采用反证法证明 \(i-nxt[i]+1\) 是最小可能匹配位置。假设存在一个可能的匹配位置 \(1\lt p \lt i-nxt[j]+1\)，如下图：

记 \(p\) 到 \(j\) 的子串长为 \(len\)，显然 \(len>nxt[i]\)。我们画出移动后的模式串 \(T\)（第三条橙色线），那么移动后第三条橙色线 \(T\) 的长为 \(len\) 的前缀等于第二条橙色线 \(p\) 到 \(j\) 的子串即 \(T\) 长为 \(j\) 的前缀的长为 \(len\) 的后缀（上下对应）。

于是在长为 \(T\) 的 \(j\) 的前缀中，长为 \(len\) 的前缀等于长为 \(len\) 的后缀，所以这个串是 \(T\) 的公共真前后缀，但是前面我们又说 \(len>nxt[i]\)，这与 \(nxt[]\) 的定义矛盾，于是假设不成立，得证。

所以下一个可能的匹配位置就为 \(i-nxt[j]+1\)，接着长度为 \(nxt[j]\) 的前缀，就可以利用我们前面匹配好的长度为 \(nxt[j]\) 的后缀匹配好，于是从 \((i-nxt[j]+1)+nxt[j]-1=i\) 继续匹配即可（相当于 \(i\) 不用改）；至于 \(j\)，由于前面 \(nxt[j]\) 为已经匹配好了，所以 \(j\leftarrow nxt[j]\) 即可。

那要是还失配呢？继续 \(j\leftarrow nxt[j]\) ，直到 \(S[i+1]=T[j+1]\) 或 \(j=0\) 为止。

结合前面前缀函数 \(nxt[]\) 的性质感性理解一下：根据性质 \(\bf{2}\)，这是一个找一遍每一个公共真前后缀的过程，根据 性质 \(\bf{1}\)，每次操作后，长度不断减小，起始点就越近，这其实是一种不断 “退而求其次” 的思路，近一点就意味着更多的重复利用之前的匹配结结果，太近的匹配不上，就往后走，走太多了，那就会超出匹配过的范围，就没有可利用的结果了，那就不是当前的 \(i\) 下需要解决的问题了。

容易写成代码：

// kmp.cpp
int n,m,nxt[M];
char s[N],t[M];
void KMP(){
	// calculate nxt[]
	for(int i=1,j=0;i<=n;i++){
		while(j&&t[j+1]!=s[i]) j=nxt[j];
		j+=(t[j+1]==s[i]);
		if(j==m){
			// do something
		}
	}
} 

注意我们原来是说比较 \(S[i+1] \neq T[j+1]\)，但是由于 \(i+1\) 的值在一轮循环中全程都不变，所以我们将 \(i\) 更新的工作交给循环提前做，我们在循环内部用 \(i\) 即可，不要写成 \(i+1\)。

还有，为什么不是 j++ 呢？因为有可能根本就无法配对，所以要判断能不能匹配，匹配上了再 ++，即 j+=(t[j+1]==s[i]);。

讲的很细了，应该代码没有什么问题，现在只剩下一个问题：怎么求前缀函数 \(nxt[]\)？

前缀函数-求法

好吧，其实前缀函数 \(nxt[]\) 的求法才是 \(\text{KMP}\) 算法最常考的内容，甚至大部分的题都不需要匹配的过程，重点都在考查对前缀函数 \(nxt[]\) 的理解。

前缀函数的求法运用了增量法，即我们在已知前面的 \(nxt[]\) 时来确定新的函数值，当然也可以说是一种 dp。

设原串为 \(s\)，接下来要求出 \(nxt[i]\)，前面的所有 \(nxt[]\) 值已知，那么显然初始状态时是 \(nxt[1]=0\)。

显然，若原串长这样：

\(\texttt{[aba]c}\cdots\texttt{[aba]}\)

其中被 \(\texttt{[ ]}\) 包裹的是最长公共真前后缀，那么这是分两种情况：

• 当 \(s[nxt[i-1]+1]=s[i]\) 时，即当加入 \(\texttt{c}\) 时，此时最长公共真前后缀变成 \(\texttt{[aba]c}\)，即有 \(nxt[i]=nxt[i-1]+1\)。
• 当 \(s[nxt[i-1]+1] \neq s[i]\)，即加入一个不是 \(\texttt{c}\) 的字符时，那就无法与前面的最长公共真前后缀吻合上了，于是 “退而求其次”：最大不行，第二小的呢？相信你也想到了，就是利用前缀函数的性质 \(\bf{2}\)，不断找更小的看看能不能吻合，找到最后，如果还没有，那么 \(nxt[i]=0\)。

同样容易写成代码：

int n,m,nxt[M];
char s[N],t[M];
void KMP(){
	nxt[1]=0;
	for(int i=2,j=0;i<=m;i++){
		while(j&&t[j+1]!=t[i]) j=nxt[j];
		j=nxt[i]=j+(t[j+1]==t[i]);
	}
	for(int i=1,j=0;i<=n;i++){
		while(j&&t[j+1]!=s[i]) j=nxt[j];
		j+=(t[j+1]==s[i]);
		if(j==m){
			// do something
		}
	}
}

对比求前缀函数 \(nxt[]\) 的代码和匹配的代码，两份代码竟惊人的相似！

这是因为，设已经求出原串的一个前缀 \(s\) 的所有前缀函数，那么此时若再添加一个字符 \(c\)，相当于是在 \((s+c)\) 中用 \(s\) 进行匹配的最后一轮的过程，只是我们不关心是否匹配好罢了，这个感性理解一下就好了。

\(\bf{KMP}\)-复杂度

我们分析前缀函数 \(nxt[]\) 的复杂度：

int m,nxt[M];
char t[M];
nxt[1]=0;
for(int i=2,j=0;i<=m;i++){
	while(j&&t[j+1]!=t[i]) j=nxt[j];
	j=nxt[i]=j+(t[j+1]==t[i]);
}

唯一有点迷的只有这个 while 了，其他都是 \(O(m)\) 的。

显然 while 中的语句是 \(O(1)\) 的，所以重点在于 while 的执行次数。

我们这么考虑，根据前缀函数的性质 \(\bf{1}\)，\(j\) 在 while 中每次至少减少 \(1\)，但是 \(j\) 仅会在每次循环中加至多 \(1\)，所以 \(j\) 的所有增加不会超过 \(m\)，于是最多进入 while 循环 \(O(m)\) 次，于是总复杂度为 \(O(m)\)。

匹配的复杂度分析类似，复杂度 \(O(n+m)\)。

综上所述，\(\texttt{KMP}\) 算法的复杂度为 \(O(n+m)\)。

容易构造出一种最坏情况，\(S=\texttt{aaa}\cdots\texttt{ab}\)，\(T=\texttt{aaa}\cdots\texttt{a}\)。

实际上，还有很多一般表现上 \(\text{KMP}\) 的字符串匹配算法，如 \(\text{BM}\)、\(\text{Sunday}\) 等等，但是 \(\text{KMP}\) 在 \(\text{OI}\) 中已经够用了，而且真正搞明白 \(\text{KMP}\) 也已经很不容易了呢~。

尾声

写完了！！！累！

本作品采用 CC BY-SA 4.0 进行许可，附加条款亦可使用。