目录
改进的多目标差分进化算法不仅可以应用在电力系统环境经济调度,换其他多目标函数和约束条件依然适用。主要是把这个工具用好,用在其他多目标经典问题上,然后就可以写一篇期刊论文。
下面是运行结果:
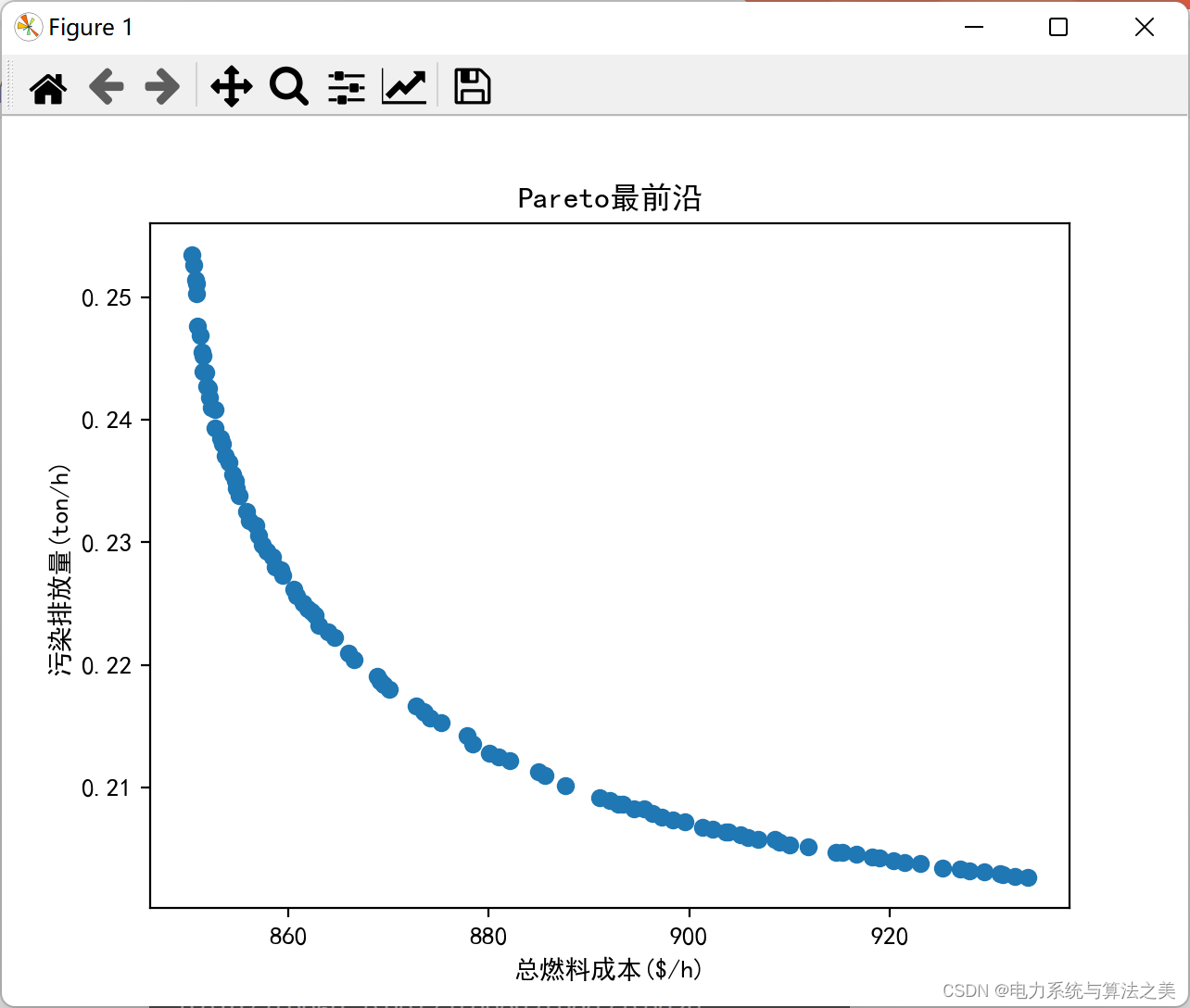
迭代一千次:

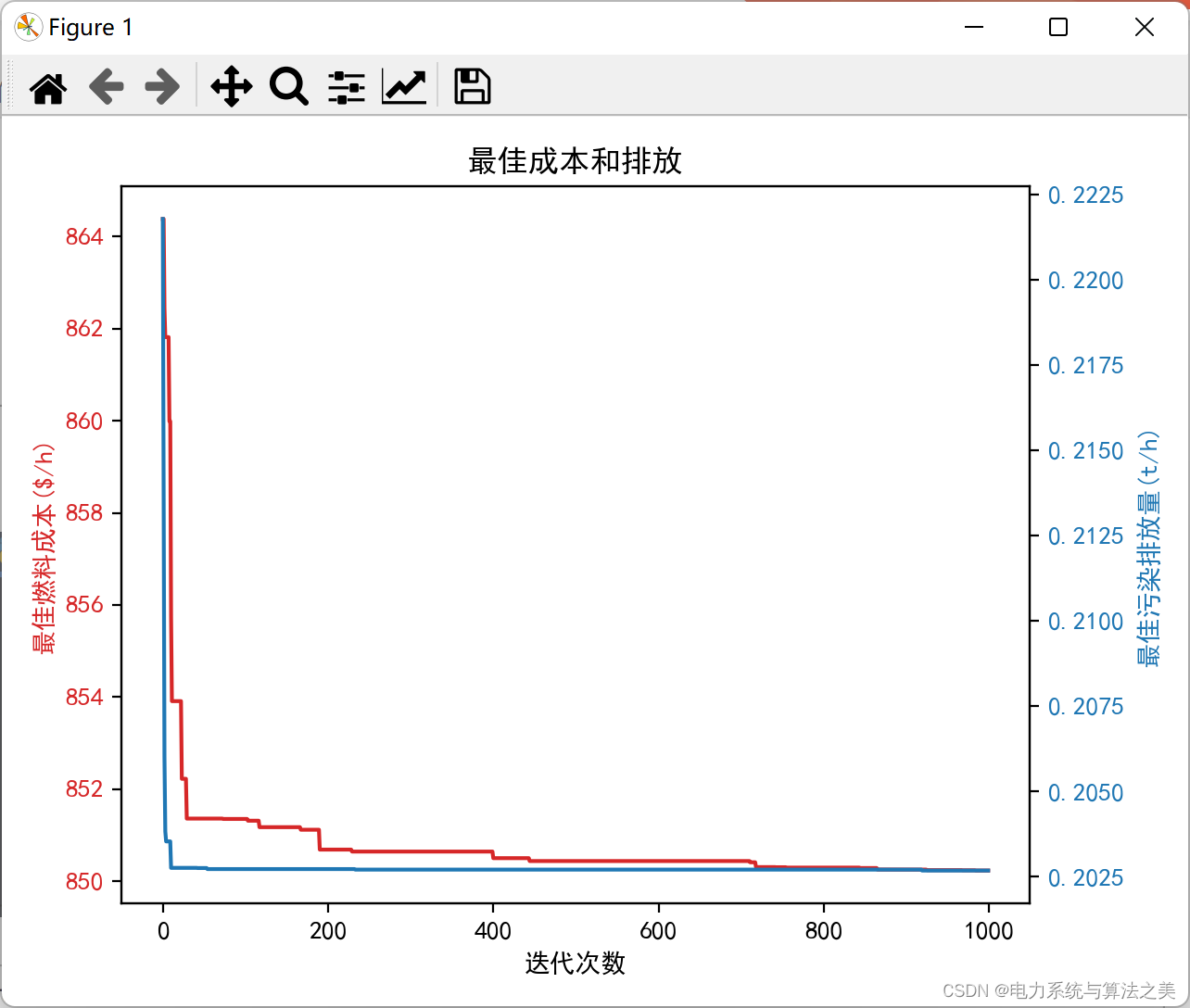

1 电力系统环境经济调度数学模型
多目标差分进化算法(Multi-objective Differential Evolution Algorithm, 缩写为MODEA)是一种针对多目标优化问题的高效计算方法。它基于经典的差分进化算法(Differential Evolution, DE),通过引入特定策略来处理多个目标函数同时优化的挑战。在电力系统环境经济调度(Environmental/Economic Dispatch, EED)问题中,MODEA得到了广泛应用,因为EED问题本身就是一个典型的多目标优化问题,需要同时考虑经济效益和环境保护两个或更多的相互冲突的目标。
电力系统环境经济调度问题概述
电力系统的环境经济调度旨在最小化发电成本的同时,限制污染物排放量,实现电力供应的经济性和环境友好性的平衡。具体而言,其主要目标通常包括:
- 最小化总发电成本:这涉及到考虑不同发电厂(如火电、水电、风电等)的边际成本,力求在满足负荷需求的前提下使总发电成本最低。
- 减少环境污染:限制硫化物、氮氧化物等污染物以及温室气体(主要是二氧化碳CO2)的排放量,符合环保政策要求。
- 保障系统安全运行:确保系统频率稳定、电压质量以及备用容量充足等。
多目标差分进化算法的应用
在解决EED问题时,MODEA通过以下几个方面发挥作用:
-
种群初始化与维护:初始化一个包含多个解(即发电厂的发电计划组合)的种群,每个解代表了一种发电策略。MODEA通过不断迭代,根据适应度函数(综合考虑经济成本和排放量等目标)评估并更新种群,逐渐逼近最优解集合(Pareto前沿)。
-
差分变异与交叉操作:基于DE算法的核心机制,对种群中的个体进行差分变异和交叉,引入随机性和多样性,探索解空间,有助于避免局部最优解并提高搜索效率。
-
多目标优化策略:采用诸如非支配排序、 crowding distance 等策略,来维持种群的多样性,确保搜索过程能够兼顾所有目标,生成Pareto最优解集而非单一最优解。
-
约束处理:在优化过程中有效处理电力系统运行的各种硬约束(如发电量上下限、网络传输限制)和软约束(如环境标准),确保生成的调度方案是实际可行的。
应用研究的意义
- 提升决策支持水平:MODEA提供了一套机制,帮助电力系统运营商在复杂的决策环境中找到平衡经济效益和环境保护的调度方案。
- 促进可持续发展:通过有效控制污染排放,助力实现能源行业的低碳转型和可持续发展目标。
- 技术与算法创新:推动电力系统优化理论与算法的进一步发展,特别是在面对更加复杂的多目标、多约束问题时展现出优越性。
总之,多目标差分进化算法在电力系统环境经济调度中的应用,不仅提高了调度的综合效益,还促进了电力行业向更加智能化、绿色化方向的发展。随着技术的不断进步和环境要求的日益严格,该领域的研究将会持续深入,算法的性能和适用性也将得到进一步提升。




2 改进的多目标差分进化算法



3 Python代码实现
3.1 结果
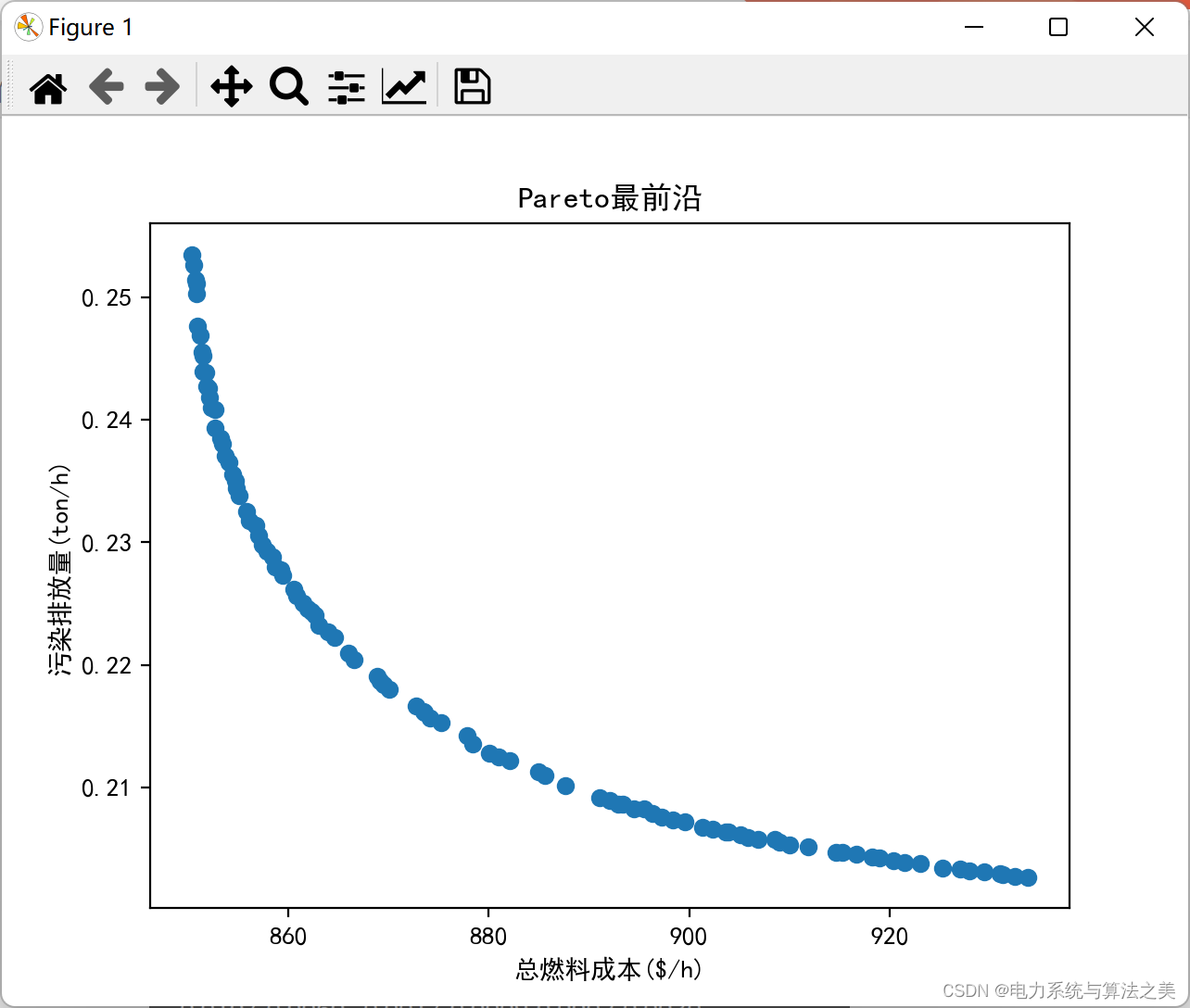
迭代500次:

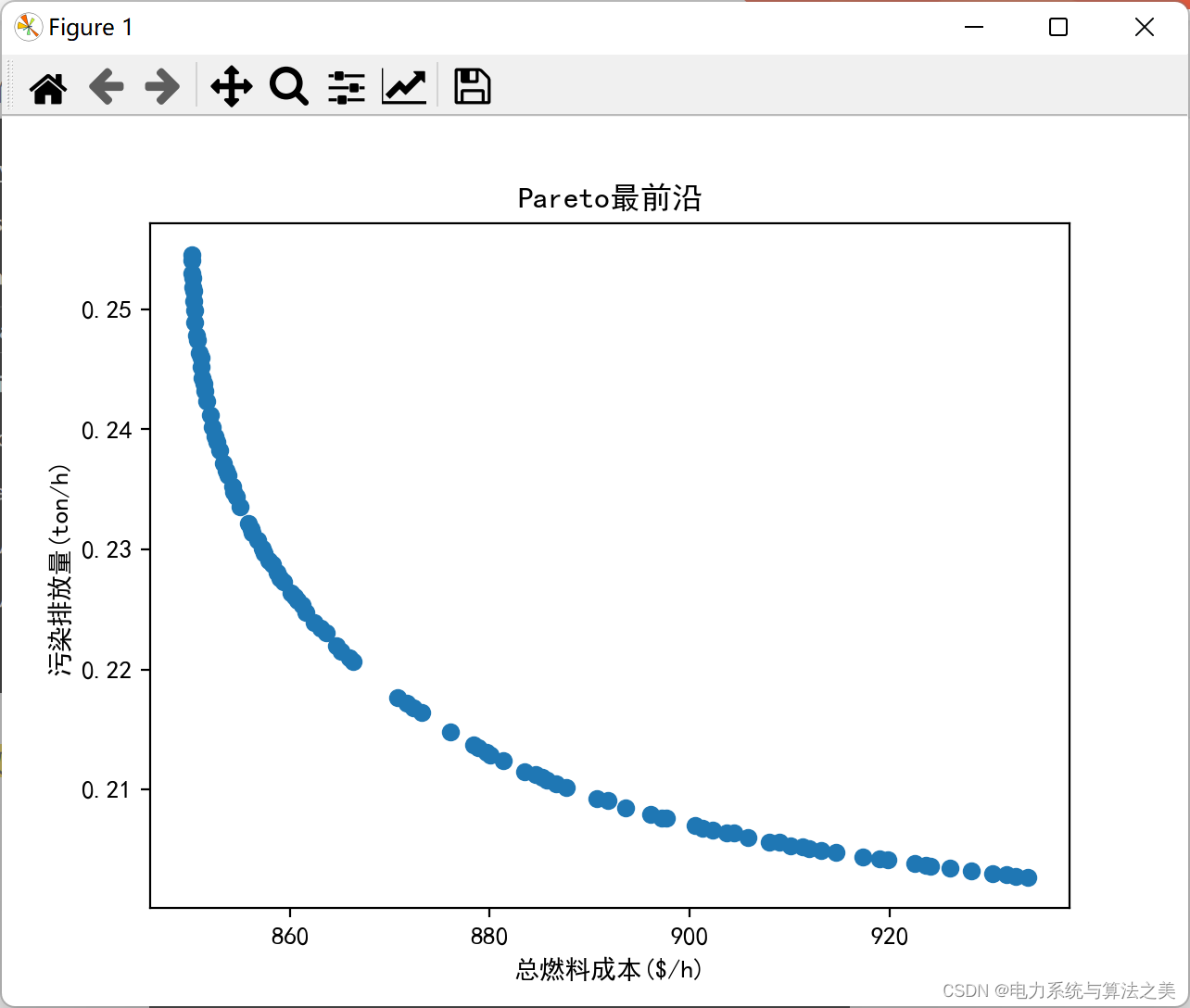
迭代一千次:

3.2 Python代码
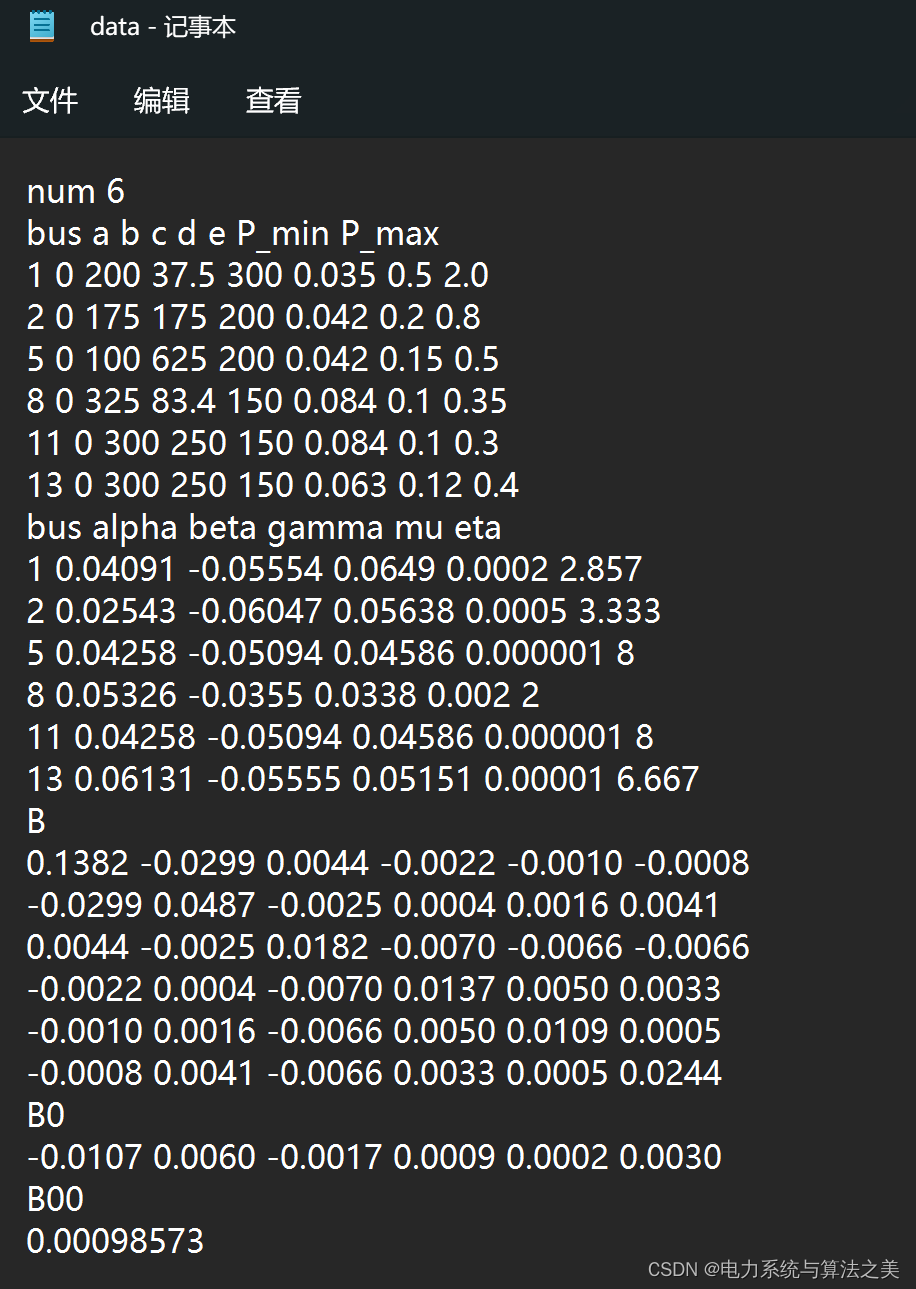
(1)数据
(2)读取数据然后书写目标函数和约束条件
#!/usr/bin/env python
# coding:utf-8
import numpy as np
import math
# from DE.initial import create_child, initialize
from constraint import constraints
"""=============读取data.txt数据==================="""
def inital_model(file): #file:data.txt这个文件
data = open(file, 'r').readlines() #读取整个文件所有行,保存在一个列表(list)变量中,每行作为一个元素
num = int(data[0].split()[-1]) #切割字符串,结果返回由字符串元素组成的一个列表,得到num=6(机组个数)
C = np.zeros([num, 5]) #存放煤耗特性系数
E = np.zeros([num, 5]) #存放排放特性系数
P = np.zeros([num, 2]) #存放机组最大出力与最小出力
B = np.zeros([num, num]) #存放B矩阵
parameters = len(data[3].split()) - 3 #第3行开始,到3+6=9行(Python从0开始计数)
for i in range(2, 2 + num):
raw_data = data[i].split()[1:]
for j in range(parameters):
C[i - 2][j] = float(raw_data[j]) #读取煤耗特性系数
P[i - 2][0] = float(raw_data[-2]) #读取机组下限
P[i - 2][1] = float(raw_data[-1]) #读取机组上限
length = len(data[2 + num].split()) - 1
for i in range(3 + num, 3 + 2 * num): #读取排放特性系数
raw_data = data[i].split()[1:]
for j in range(length):
E[i - 3 - num][j] = float(raw_data[j]) #排放特性系数
for i in range(4 + 2 * num, 4 + 3 * num): #读取B矩阵
raw_data = data[i].split()
B[i - 4 - 2 * num] = np.array(list(map(float, raw_data)))
B_0 = np.array(list(map(float, data[5 + 3 * num].split())))
B_00 = float(data[7 + 3 * num])
return num, C, E, P, B, B_0, B_00
"""=====总燃料成本==========="""
def costfun(uid, load, C, P=None):
if P is not None: #如果满足机组上下限
return load * (C[uid][2] * load + C[uid][1]) + C[uid][0] + math.fabs(C[uid][3] *
math.sin(C[uid][4] * (P[uid][0] - load)))
return load * (C[uid][2] * load + C[uid][1]) + C[uid][0]
"""======总污染排放量=========="""
def emission(uid, load, E, flag=True):
if E[0][3] != 0 and flag:
return (E[uid][0] + (E[uid][1] + E[uid][2] * load) * load) + E[uid][3] * math.exp(E[uid][4] * load)
else:
return load * (E[uid][2] * load + E[uid][1]) + E[uid][0]
class Model:
def __init__(self, file):
self.nGen, self.C, self.E, self.P, self.B, self.B_0, self.B_00 = inital_model(file)
def constraint(self):
return constraints
""'======运行===================='
if __name__ == '__main__':
demand = 2.834 #负荷需求
model = Model('../data.txt')
print("===============排放系数===============")
print(model.E)
exit(0)
pop = np.array([0.1917, 0.3804, 0.5603, 0.7154, 0.6009, 0.3804]) #六个机组出力
fuel = 0
emis = 0
for i in range(len(pop)): #遍历六个机组
fuel += costfun(i, pop[i], model.C, model.P)
emis += emission(i, pop[i], model.E, flag=True)
print(fuel, emis)
print(constraints(pop, model, demand))
exit(0)
(3)主函数,运行
"""========开始运行============="""
if __name__ == '__main__':
demand = 2.834
model = Model('../data.txt')
arguments = {'nIter': 1000, 'nPop': 200, 'nArc': 100, 'nGen': 6, 'F': 0.6, 'CR': 0, 'init': 1, 'mutation': 0}
DE = MMODE(model=model, **arguments)
DE.solve(demand)
print(DE.finalY.shape)
n = range(DE.nIter)
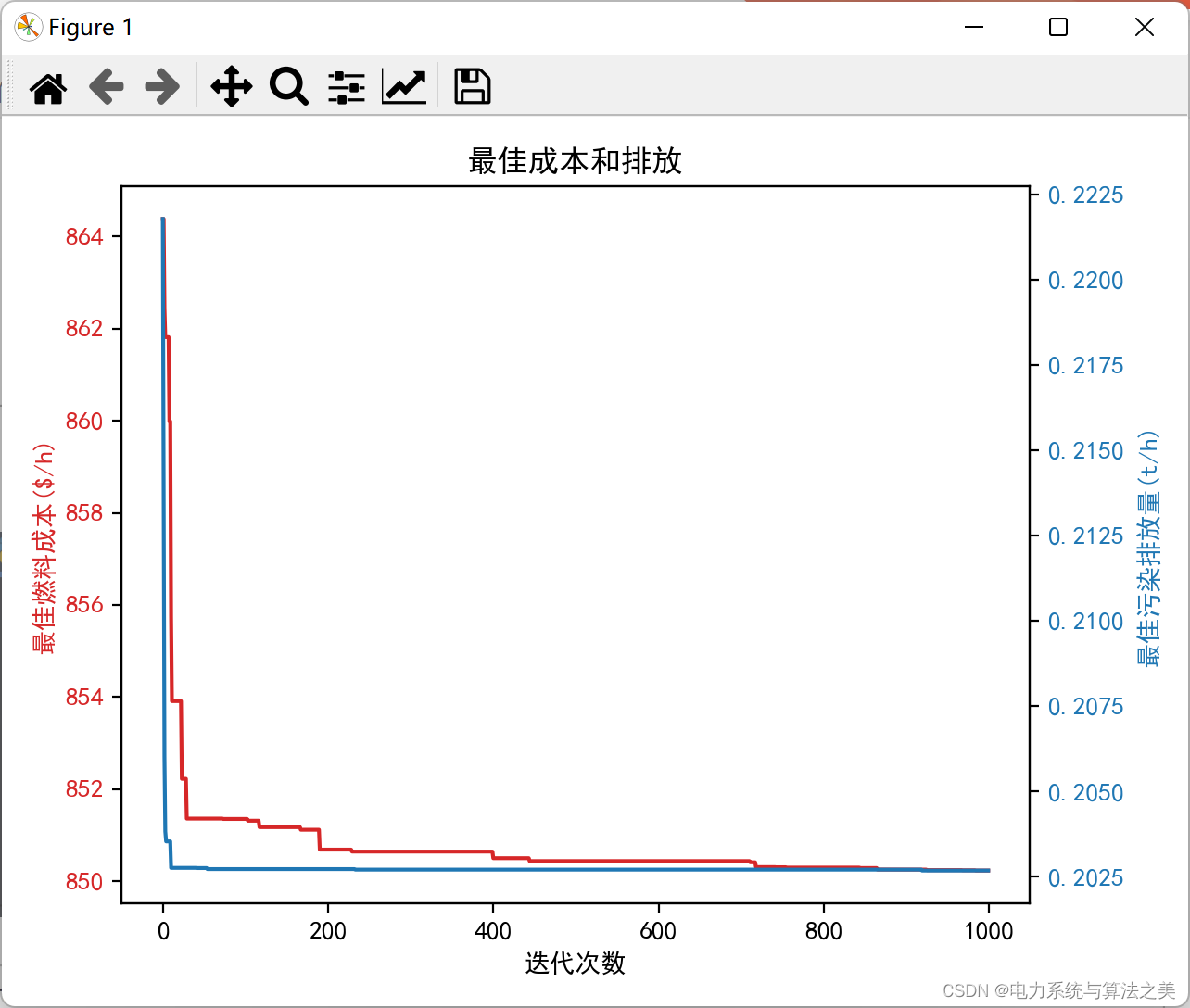
fig, ax1 = plt.subplots()
color = 'tab:red'
ax1.set_xlabel('迭代次数')
ax1.set_ylabel('最佳燃料成本($/h)', color=color)
ax1.plot(n, DE.bestC, color=color)
ax1.tick_params(axis='y', labelcolor=color)
ax2 = ax1.twinx() # second y axis
color = 'tab:blue'
ax2.set_ylabel('最佳污染排放量(t/h)', color=color)
ax2.plot(n, DE.bestE, color=color)
ax2.tick_params(axis='y', labelcolor=color)
plt.title('最佳成本和排放')
fig.tight_layout()
plt.show()