Python 金融编程第二版(GPT 重译)(三)
原文:
annas-archive.org/md5/d2f94efd019a2e2cb5c4fa9f260d63c译者:飞龙
第六章:面向对象编程
软件工程的目的是控制复杂性,而不是创建它。
Pamela Zave
介绍
面向对象编程(OOP)是当今最流行的编程范式之一。正确使用时,它与过程式编程相比提供了许多优势。在许多情况下,OOP 似乎特别适用于金融建模和实施金融算法。然而,也有许多对 OOP 持批评态度的人,对 OOP 的单个方面甚至整个范式表示怀疑。本章对此持中立态度,认为 OOP 是一个重要的工具,可能不是每个问题的最佳解决方案,但应该是程序员和从事金融工作的量化人员的手头工具之一。
随着 OOP 的出现,一些新的术语也随之而来。本书和本章的最重要术语是(更多细节如下):
类
对象类的抽象定义。例如,一个人类。
属性
类的特性(类属性)或类的实例(实例属性)的一个特征。例如,是哺乳动物或眼睛的颜色。
方法
可以在类上实现的操作。例如,行走。
参数
一个方法接受的输入参数以影响其行为。例如,三个步骤。
对象
类的一个实例。例如,有蓝眼睛的 Sandra。
实例化
创建基于抽象类的特定对象的过程。
转换为 Python 代码,实现人类示例的简单类可能如下所示。
In [1]: class HumanBeing(object): 
def __init__(self, first_name, eye_color): 
self.first_name = first_name 
self.eye_color = eye_color 
self.position = 0 
def walk_steps(self, steps): 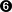
self.position += steps 
类定义语句。
在实例化时调用的特殊方法。
名字属性初始化为参数值。
眼睛颜色属性初始化为参数值。
位置属性初始化为 0。
使用steps作为参数的步行方法定义。
给定steps值后改变位置的代码。
根据类定义,可以实例化并使用一个新的 Python 对象。
In [2]: Sandra = HumanBeing('Sandra', 'blue') 
In [3]: Sandra.first_name 
Out[3]: 'Sandra'
In [4]: Sandra.position 
Out[4]: 0
In [5]: Sandra.walk_steps(5) 
In [6]: Sandra.position 
Out[6]: 5
实例化。
访问属性值。
调用方法。
访问更新后的position值。
有几个人类方面可能支持使用 OOP:
自然的思考方式
人类思维通常围绕着现实世界或抽象对象展开,比如汽车或金融工具。面向对象编程适合模拟具有其特征的这类对象。
降低复杂性
通过不同的方法,面向对象编程有助于降低问题或算法的复杂性,并逐个特征进行建模。
更好的用户界面
在许多情况下,面向对象编程可以实现更美观的用户界面和更紧凑的代码。例如,当查看NumPy的ndarray类或pandas的DataFrame类时,这一点变得显而易见。
Python 建模的方式
独立于面向对象编程的优缺点,它只是 Python 中的主导范式。这也是“在 Python 中一切皆为对象。”这句话的由来。面向对象编程还允许程序员构建自定义类,其实例的行为与标准 Python 类的任何其他实例相同。
也有一些技术方面可能支持面向对象编程:
抽象化
使用属性和方法可以构建对象的抽象、灵活的模型——重点放在相关的内容上,忽略不需要的内容。在金融领域,这可能意味着拥有一个以抽象方式模拟金融工具的通用类。这种类的实例将是由投资银行设计和提供的具体金融产品,例如。
模块化
面向对象编程简化了将代码拆分为多个模块的过程,然后将这些模块链接起来形成完整的代码基础。例如,可以通过一个类或两个类来建模股票上的欧式期权,一个用于基础股票,另一个用于期权本身。
继承
继承指的是一个类可以从另一个类继承属性和方法的概念。在金融领域,从一个通用的金融工具开始,下一个级别可能是一个通用的衍生金融工具,然后是一个欧式期权,再然后是一个欧式看涨期权。每个类都可以从更高级别的类中继承属性和方法。
聚合
聚合指的是一个对象至少部分由多个其他对象组成,这些对象可能是独立存在的。模拟欧式看涨期权的类可能具有其他对象的属性,例如基础股票和用于贴现的相关短期利率。表示股票和短期利率的对象也可以被其他对象独立使用。
组合
组合与聚合类似,但是这里的单个对象不能独立存在。考虑一个定制的固定利率互换合同和一个浮动利率互换合同。这两个腿不能独立于互换合同本身存在。
多态性
多态性可以呈现多种形式。在 Python 上下文中特别重要的是所谓的鸭子类型。这指的是可以在许多不同类及其实例上实现标准操作,而不需要准确知道正在处理的特定对象是什么。对于金融工具类,这可能意味着可以调用一个名为 get_current_price() 的方法,而不管对象的具体类型是什么(股票、期权、互换等)。
封装
此概念指的是仅通过公共方法访问类内部数据的方法。模拟股票的类可能有一个属性 current_stock_price。封装将通过方法 get_current_stock_price() 提供对属性值的访问,并将数据隐藏(使其私有化)。这种方法可能通过仅使用和可能更改属性值来避免意外效果。但是,对于如何使数据在 Python 类中私有化存在限制。
在更高层面上,软件工程中的两个主要目标可以总结如下:
可重用性
继承和多态等概念提高了代码的可重用性,增加了程序员的效率和生产力。它们还简化了代码的维护。
非冗余性
与此同时,这些方法允许构建几乎不冗余的代码,避免双重实现工作,减少调试和测试工作以及维护工作量。它还可能导致更小的总体代码基础。
本章按如下方式组织:
“Python 对象概览”
下一节将通过面向对象编程的视角简要介绍一些 Python 对象。
“Python 类基础”
本节介绍了 Python 中面向对象编程的核心要素,并以金融工具和投资组合头寸为主要示例。
“Python 数据模型”
本节讨论了 Python 数据模型的重要元素以及某些特殊方法所起的作用。
Python 对象概览
本节通过面向对象编程程序员的眼光简要介绍了一些标准对象,这些对象在前一节中已经遇到过。
int
为了简单起见,考虑一个整数对象。即使对于这样一个简单的 Python 对象,主要的面向对象编程(OOP)特征也是存在的。
In [7]: n = 5 
In [8]: type(n) 
Out[8]: int
In [9]: n.numerator 
Out[9]: 5
In [10]: n.bit_length() 
Out[10]: 3
In [11]: n + n 
Out[11]: 10
In [12]: 2 * n 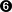
Out[12]: 10
In [13]: n.__sizeof__() 
Out[13]: 28
新实例 n。
对象的类型。
一个属性。
一个方法。
应用 + 运算符(加法)。
应用 * 运算符(乘法)。
调用特殊方法__sizeof__()以获取内存使用情况(以字节为单位)。¹
列表
list对象有一些额外的方法,但基本上表现方式相同。
In [14]: l = [1, 2, 3, 4] 
In [15]: type(l) 
Out[15]: list
In [16]: l[0] 
Out[16]: 1
In [17]: l.append(10) 
In [18]: l + l 
Out[18]: [1, 2, 3, 4, 10, 1, 2, 3, 4, 10]
In [19]: 2 * l 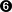
Out[19]: [1, 2, 3, 4, 10, 1, 2, 3, 4, 10]
In [20]: sum(l) 
Out[20]: 20
In [21]: l.__sizeof__() 
Out[21]: 104
新实例l。
对象的类型。
通过索引选择元素。
一个方法。
应用+运算符(连接)。
应用*运算符(连接)。
应用标准 Python 函数sum()。
调用特殊方法__sizeof__()以获取内存使用情况(以字节为单位)。
ndarray
int和list对象是标准的 Python 对象。NumPy的ndarray对象是一个来自开源包的“自定义”对象。
In [22]: import numpy as np 
In [23]: a = np.arange(16).reshape((4, 4)) 
In [24]: a 
Out[24]: array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
In [25]: type(a) 
Out[25]: numpy.ndarray
导入numpy。
新实例a。
对象的类型。
尽管ndarray对象不是标准对象,但在许多情况下表现得就像是一个标准对象——这要归功于下文中解释的 Python 数据模型。
In [26]: a.nbytes 
Out[26]: 128
In [27]: a.sum() 
Out[27]: 120
In [28]: a.cumsum(axis=0) 
Out[28]: array([[ 0, 1, 2, 3],
[ 4, 6, 8, 10],
[12, 15, 18, 21],
[24, 28, 32, 36]])
In [29]: a + a 
Out[29]: array([[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22],
[24, 26, 28, 30]])
In [30]: 2 * a 
Out[30]: array([[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22],
[24, 26, 28, 30]])
In [31]: sum(a) 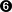
Out[31]: array([24, 28, 32, 36])
In [32]: np.sum(a) 
Out[32]: 120
In [33]: a.__sizeof__() 
Out[33]: 112
一个属性。
一个方法(聚合)。
一个方法(没有聚合)。
应用+运算符(加法)。
应用*运算符(乘法)。
应用标准 Python 函数sum()。
应用NumPy通用函数np.sum()。
调用特殊方法__sizeof__()以获取内存使用情况(以字节为单位)。
DataFrame
最后,快速查看pandas的DataFrame对象,因为其行为大多与ndarray对象相同。首先,基于ndarray对象实例化DataFrame对象。
In [34]: import pandas as pd 
In [35]: df = pd.DataFrame(a, columns=list('abcd')) 
In [36]: type(df) 
Out[36]: pandas.core.frame.DataFrame
导入pandas。
新实例df。
对象的类型。
其次,查看属性、方法和操作。
In [37]: df.columns 
Out[37]: Index(['a', 'b', 'c', 'd'], dtype='object')
In [38]: df.sum() 
Out[38]: a 24
b 28
c 32
d 36
dtype: int64
In [39]: df.cumsum() 
Out[39]: a b c d
0 0 1 2 3
1 4 6 8 10
2 12 15 18 21
3 24 28 32 36
In [40]: df + df 
Out[40]: a b c d
0 0 2 4 6
1 8 10 12 14
2 16 18 20 22
3 24 26 28 30
In [41]: 2 * df 
Out[41]: a b c d
0 0 2 4 6
1 8 10 12 14
2 16 18 20 22
3 24 26 28 30
In [42]: np.sum(df) 
Out[42]: a 24
b 28
c 32
d 36
dtype: int64
In [43]: df.__sizeof__() 
Out[43]: 208
一个属性。
一个方法(聚合)。
一个方法(无聚合)。
应用+运算符(加法)。
应用*运算符(乘法)。
应用NumPy通用函数np.sum()。
调用特殊方法__sizeof__()以获取以字节为单位的内存使用情况。
Python 类的基础知识
本节涉及主要概念和具体语法,以利用 Python 中的 OOP。当前的背景是构建自定义类来模拟无法轻松、高效或适当地由现有 Python 对象类型建模的对象类型。在金融工具的示例中,只需两行代码即可创建一个新的 Python 类。
In [44]: class FinancialInstrument(object): 
pass 
In [45]: fi = FinancialInstrument() 
In [46]: type(fi) 
Out[46]: __main__.FinancialInstrument
In [47]: fi 
Out[47]: <__main__.FinancialInstrument at 0x10a21c828>
In [48]: fi.__str__() 
Out[48]: '<__main__.FinancialInstrument object at 0x10a21c828>'
In [49]: fi.price = 100 
In [50]: fi.price 
Out[50]: 100
类定义语句。²
一些代码;这里只是pass关键字。
一个名为fi的类的新实例。
每个 Python 对象都带有某些特殊属性和方法(来自object);这里调用了用于检索字符串表示的特殊方法。
所谓的数据属性 —— 与常规属性相对 —— 可以为每个对象即时定义。
一个重要的特殊方法是__init__,它在每次实例化对象时被调用。它以对象自身(按照惯例为self)和可能的多个其他参数作为参数。除了实例属性之外
In [51]: class FinancialInstrument(object):
author = 'Yves Hilpisch' 
def __init__(self, symbol, price): 
self.symbol = symbol 
self.price = price 
In [52]: FinancialInstrument.author 
Out[52]: 'Yves Hilpisch'
In [53]: aapl = FinancialInstrument('AAPL', 100) 
In [54]: aapl.symbol 
Out[54]: 'AAPL'
In [55]: aapl.author 
Out[55]: 'Yves Hilpisch'
In [56]: aapl.price = 105 
In [57]: aapl.price 
Out[57]: 105
类属性的定义(=每个实例都继承的)。
在初始化期间调用特殊方法__init__。
实例属性的定义(=每个实例都是个别的)。
一个名为fi的类的新实例。
访问实例属性。
访问类属性。
更改实例属性的值。
金融工具的价格经常变动,金融工具的符号可能不会变动。为了向类定义引入封装,可以定义两个方法get_price()和set_price()。接下来的代码还额外继承了之前的类定义(不再继承自object)。
In [58]: class FinancialInstrument(FinancialInstrument): 
def get_price(self): 
return self.price 
def set_price(self, price): 
self.price = price 
In [59]: fi = FinancialInstrument('AAPL', 100) 
In [60]: fi.get_price() 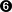
Out[60]: 100
In [61]: fi.set_price(105) 
In [62]: fi.get_price() 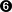
Out[62]: 105
In [63]: fi.price 
Out[63]: 105
通过从上一个版本继承的方式进行类定义。
定义get_price方法。
定义set_price方法……
……并根据参数值更新实例属性值。
基于新的类定义创建一个名为fi的新实例。
调用get_price()方法来读取实例属性值。
通过set_price()更新实例属性值。
直接访问实例属性。
封装通常的目标是隐藏用户对类的操作中的数据。添加相应的方法,有时称为getter和setter方法,是实现此目标的一部分。然而,这并不阻止用户直接访问和操作实例属性。这就是私有实例属性发挥作用的地方。它们由两个前导下划线定义。
In [64]: class FinancialInstrument(object):
def __init__(self, symbol, price):
self.symbol = symbol
self.__price = price 
def get_price(self):
return self.__price
def set_price(self, price):
self.__price = price
In [65]: fi = FinancialInstrument('AAPL', 100)
In [66]: fi.get_price() 
Out[66]: 100
In [67]: fi.__price 
----------------------------------------
AttributeErrorTraceback (most recent call last)
<ipython-input-67-74c0dc05c9ae> in <module>()
----> 1 fi.__price 
AttributeError: 'FinancialInstrument' object has no attribute '__price'
In [68]: fi._FinancialInstrument__price 
Out[68]: 100
In [69]: fi._FinancialInstrument__price = 105 
In [70]: fi.set_price(100) 
价格被定义为私有实例属性。
方法get_price()返回其值。
尝试直接访问属性会引发错误。
通过在类名前添加单个下划线,仍然可以直接访问和操作。
将价格恢复到其原始值。
注意
尽管封装基本上可以通过私有实例属性和处理它们的方法来实现 Python 类,但无法完全强制隐藏数据不让用户访问。从这个意义上说,这更像是 Python 中的一种工程原则,而不是 Python 类的技术特性。
考虑另一个模拟金融工具投资组合头寸的类。通过两个类,聚合的概念很容易说明。PortfolioPosition类的一个实例将FinancialInstrument类的一个实例作为属性值。添加一个实例属性,比如position_size,然后可以计算出例如头寸价值。
In [71]: class PortfolioPosition(object):
def __init__(self, financial_instrument, position_size):
self.position = financial_instrument 
self.__position_size = position_size 
def get_position_size(self):
return self.__position_size
def update_position_size(self, position_size):
self.__position_size = position_size
def get_position_value(self):
return self.__position_size * \
self.position.get_price() 
In [72]: pp = PortfolioPosition(fi, 10)
In [73]: pp.get_position_size()
Out[73]: 10
In [74]: pp.get_position_value() 
Out[74]: 1000
In [75]: pp.position.get_price() 
Out[75]: 100
In [76]: pp.position.set_price(105) 
In [77]: pp.get_position_value() 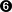
Out[77]: 1050
基于FinancialInstrument类的实例的实例属性。
PortfolioPosition类的私有实例属性。
根据属性计算位置值。
附加到实例属性对象的方法可以直接访问(也可能被隐藏)。
更新金融工具的价格。
根据更新后的价格计算新位置值。
Python 数据模型
前一节的示例已经突出了所谓的 Python 数据或对象模型的一些方面(参见https://docs.python.org/3/reference/datamodel.html)。Python 数据模型允许设计与 Python 基本语言构造一致交互的类。除其他外,它支持(参见 Ramalho(2015),第 4 页)以下任务和结构:
-
迭代
-
集合处理
-
属性访问
-
运算符重载
-
函数和方法调用
-
对象创建和销毁
-
字符串表示(例如,用于打印)
-
受管理的上下文(即
with块)。
由于 Python 数据模型非常重要,本节专门介绍了一个示例,探讨了其中的几个方面。示例可在 Ramalho(2015)的书中找到,并进行了微调。它实现了一个一维,三元素向量的类(想象一下欧几里德空间中的向量)。首先,特殊方法__init__:
In [78]: class Vector(object):
def __init__(self, x=0, y=0, z=0): 
self.x = x 
self.y = y 
self.z = z 
In [79]: v = Vector(1, 2, 3) 
In [80]: v 
Out[80]: <__main__.Vector at 0x10a245d68>
三个预初始化的实例属性(想象成三维空间)。
名为v的类的新实例。
默认字符串表示。
特殊方法__str__允许定义自定义字符串表示。
In [81]: class Vector(Vector):
def __repr__(self):
return 'Vector(%r, %r, %r)' % (self.x, self.y, self.z)
In [82]: v = Vector(1, 2, 3)
In [83]: v 
Out[83]: Vector(1, 2, 3)
In [84]: print(v) 
Vector(1, 2, 3)
新的字符串表示。
abs()和bool()是两个标准的 Python 函数,它们在Vector类上的行为可以通过特殊方法__abs__和__bool__来定义。
In [85]: class Vector(Vector):
def __abs__(self):
return (self.x ** 2 + self.y ** 2 +
self.z ** 2) ** 0.5 
def __bool__(self):
return bool(abs(self))
In [86]: v = Vector(1, 2, -1) 
In [87]: abs(v)
Out[87]: 2.449489742783178
In [88]: bool(v)
Out[88]: True
In [89]: v = Vector() 
In [90]: v 
Out[90]: Vector(0, 0, 0)
In [91]: abs(v)
Out[91]: 0.0
In [92]: bool(v)
Out[92]: False
返回给定三个属性值的欧几里德范数。
具有非零属性值的新Vector对象。
仅具有零属性值的新Vector对象。
如多次显示的那样,+和*运算符几乎可以应用于任何 Python 对象。其行为是通过特殊方法__add__和__mul__定义的。
In [93]: class Vector(Vector):
def __add__(self, other):
x = self.x + other.x
y = self.y + other.y
z = self.z + other.z
return Vector(x, y, z) 
def __mul__(self, scalar):
return Vector(self.x * scalar,
self.y * scalar,
self.z * scalar) 
In [94]: v = Vector(1, 2, 3)
In [95]: v + Vector(2, 3, 4)
Out[95]: Vector(3, 5, 7)
In [96]: v * 2
Out[96]: Vector(2, 4, 6)
在这种情况下,两个特殊方法都返回自己的类型对象。
另一个标准的 Python 函数是 len(),它给出对象的长度,即元素的数量。当在对象上调用时,此函数访问特殊方法 __len__。另一方面,特殊方法 __getitem__ 使通过方括号表示法进行索引成为可能。
In [97]: class Vector(Vector):
def __len__(self):
return 3 
def __getitem__(self, i):
if i in [0, -3]: return self.x
elif i in [1, -2]: return self.y
elif i in [2, -1]: return self.z
else: raise IndexError('Index out of range.')
In [98]: v = Vector(1, 2, 3)
In [99]: len(v)
Out[99]: 3
In [100]: v[0]
Out[100]: 1
In [101]: v[-2]
Out[101]: 2
In [102]: v[3]
----------------------------------------
IndexErrorTraceback (most recent call last)
<ipython-input-102-0f5531c4b93d> in <module>()
----> 1 v[3]
<ipython-input-97-eef2cdc22510> in __getitem__(self, i)
7 elif i in [1, -2]: return self.y
8 elif i in [2, -1]: return self.z
----> 9 else: raise IndexError('Index out of range.')
IndexError: Index out of range.
Vector 类的所有实例都有长度为三。
最后,特殊方法 __iter__ 定义了对对象元素进行迭代的行为。定义了此操作的对象称为可迭代的。例如,所有集合和容器都是可迭代的。
In [103]: class Vector(Vector):
def __iter__(self):
for i in range(len(self)):
yield self[i]
In [104]: v = Vector(1, 2, 3)
In [105]: for i in range(3): 
print(v[i]) 
1
2
3
In [106]: for coordinate in v: 
print(coordinate) 
1
2
3
使用索引值进行间接迭代(通过__getitem__)。
对类实例进行直接迭代(使用__iter__)。
提示
Python 数据模型允许定义与标准 Python 操作符、函数等无缝交互的 Python 类。这使得 Python 成为一种相当灵活的编程语言,可以轻松地通过新类和对象类型进行增强。
总之,子节 “向量类” 在单个代码块中提供了 Vector 类的定义。
结论
本章从理论上和基于 Python 示例介绍了面向对象编程(OOP)的概念和方法。OOP 是 Python 中使用的主要编程范式之一。它不仅允许建模和实现相当复杂的应用程序,还允许创建自定义对象,这些对象由于灵活的 Python 数据模型,与标准 Python 对象表现得相似。尽管有许多批评者反对 OOP,但可以肯定地说,当达到一定复杂程度时,它为 Python 程序员和量化人员提供了强大的手段和工具。在 [Link to Come] 中讨论和展示的衍生定价包呈现了这样一个情况,其中 OOP 似乎是唯一合理的编程范式,以处理固有的复杂性和对抽象的需求。
更多资源
关于面向对象编程以及特别是 Python 编程和 Python OOP 的一般和宝贵的在线资源:
有关 Python 面向对象编程(OOP)和 Python 数据模型的书籍资源:
- Ramalho, Luciano(2016):流畅的 Python。 O’Reilly,北京等。
Python 代码
向量类
In [107]: class Vector(object):
def __init__(self, x=0, y=0, z=0):
self.x = x
self.y = y
self.z = z
def __repr__(self):
return 'Vector(%r, %r, %r)' % (self.x, self.y, self.z)
def __abs__(self):
return (self.x ** 2 + self.y ** 2 + self.z ** 2) ** 0.5
def __bool__(self):
return bool(abs(self))
def __add__(self, other):
x = self.x + other.x
y = self.y + other.y
z = self.z + other.z
return Vector(x, y, z)
def __mul__(self, scalar):
return Vector(self.x * scalar,
self.y * scalar,
self.z * scalar)
def __len__(self):
return 3
def __getitem__(self, i):
if i in [0, -3]: return self.x
elif i in [1, -2]: return self.y
elif i in [2, -1]: return self.z
else: raise IndexError('Index out of range.')
def __iter__(self):
for i in range(len(self)):
yield self[i]
¹ Python 中的特殊属性和方法以双下划线开头和结尾,例如 __XYZ__。
² 类名采用驼峰命名法是推荐的方式。然而,如果没有歧义,也可以采用小写命名,比如financial_instrument。
第七章:数据可视化
使用图片。一图胜千言。
阿瑟·布里斯班(1911 年)
本章介绍了matplotlib和plotly库的基本可视化能力。
尽管有许多其他可用的可视化库,但matplotlib已经确立了自己作为基准,并且在许多情况下是一个强大而可靠的可视化工具。在标准绘图方面易于使用,在更复杂的绘图和定制方面灵活。此外,它与NumPy和pandas及它们提供的数据结构紧密集成。
matplotlib仅允许以位图形式(例如 PNG 或 JPG 格式)生成图。另一方面,现代网络技术允许基于数据驱动文档(D3.js)标准创建漂亮的交互式图表,例如,可以缩放以更详细地检查某些区域。一个非常方便的库,可以使用 Python 创建这样的 D3.js 图表,是plotly。一个小的附加库,称为Cufflinks,将plotly与pandas的DataFrame对象紧密集成,可以创建最受欢迎的金融图表(如蜡烛图)
本章主要涵盖以下主题:
“静态 2D 绘图”
本节介绍了matplotlib,并呈现了一些典型的 2D 绘图,从最简单的到具有两个比例尺或不同子图的更高级的绘图。
“静态 3D 绘图”
基于matplotlib,介绍了一些在特定金融应用中有用的 3D 绘图。
“交互式 2D 绘图”
本节介绍了plotly和Cufflinks,用于创建交互式 2D 绘图。利用Cufflinks的QuantFigure功能,本节还涉及典型的金融绘图,例如在技术股票分析中使用的绘图。
本章无法全面涵盖使用Python、matplotlib或plotly进行数据可视化的所有方面,但它提供了这些包在金融领域的基本和重要功能的一些示例。其他示例也可以在后面的章节中找到。例如,第八章更深入地介绍了如何使用pandas库可视化金融时间序列数据。
静态 2D 绘图
在创建样本数据并开始绘图之前,首先进行一些导入和自定义:
In [1]: import matplotlib as mpl 
In [2]: mpl.__version__ 
Out[2]: '2.0.2'
In [3]: import matplotlib.pyplot as plt 
In [4]: plt.style.use('seaborn') 
In [5]: mpl.rcParams['font.family'] = 'serif' 
In [6]: %matplotlib inline
使用常见缩写mpl导入了matplotlib。
使用的matplotlib版本。
将所有图的字体设置为serif。
使用常见缩写plt导入了主要的绘图(子)包。
将绘图样式设置为seaborn(请参阅,例如,此处的概述)。
一维数据集
在接下来的所有内容中,我们将绘制存储在NumPy的ndarray对象或pandas的DataFrame对象中的数据。然而,matplotlib当然也能够绘制存储在不同Python格式中的数据,比如list对象。最基本但相当强大的绘图函数是plt.plot()。原则上,它需要两组数字:
-
x值:包含x坐标(横坐标值)的列表或数组 -
y值:包含y坐标(纵坐标值)的列表或数组
提供的x和y值的数量必须相匹配,当然了。考虑下面的代码,其输出如图 7-1 所示。
In [7]: import numpy as np
In [8]: np.random.seed(1000) 
In [9]: y = np.random.standard_normal(20) 
In [10]: x = np.arange(len(y)) 
plt.plot(x, y); 
# plt.savefig('../../images/ch07/mpl_01')
为了可重复性,设置随机数生成器的种子。
绘制随机数(y 值)。
固定整数(x 值)。
使用x和y对象调用plt.plot()函数。

图 7-1. 绘制给定的 x 和 y 值
plt.plot()注意到当您传递一个ndarray对象时。在这种情况下,无需提供x值的“额外”信息。如果您只提供y值,则plot将索引值视为相应的x值。因此,以下单行代码生成完全相同的输出(参见图 7-2):
In [11]: plt.plot(y);
# plt.savefig('../../images/ch07/mpl_02')

图 7-2. 绘制给定的ndarray对象的数据
NumPy 数组和 matplotlib
您可以简单地将NumPy的ndarray对象传递给matplotlib函数。matplotlib能够解释数据结构以简化绘图。但是,请注意不要传递过大和/或复杂的数组。
由于大多数ndarray方法再次返回一个ndarray对象,因此您还可以通过附加方法(甚至在某些情况下可以是多个方法)来传递您的对象。通过在样本数据上调用cumsum()方法,我们得到了这些数据的累积和,正如预期的那样,得到了不同的输出(参见图 7-3):
In [12]: plt.plot(y.cumsum());
# plt.savefig('../../images/ch07/mpl_03')

图 7-3. 绘制给定一个带有附加方法的ndarray对象
通常,默认的绘图样式不能满足报告、出版物等的典型要求。例如,您可能希望自定义使用的字体(例如,与LaTeX字体兼容),在轴上标记标签,或者绘制网格以提高可读性。这就是绘图样式发挥作用的地方(见上文)。此外,matplotlib提供了大量函数来自定义绘图样式。有些函数很容易访问;对于其他一些函数,需要深入挖掘。例如,很容易访问的是那些操作轴的函数以及与网格和标签相关的函数(参见图 7-4):
In [13]: plt.plot(y.cumsum())
plt.grid(False); 
# plt.savefig('../../images/ch07/mpl_04')
关闭网格。

图 7-4。没有网格的图
plt.axis()的其他选项在表 7-1 中给出,其中大多数必须作为string对象传递。
表 7-1。plt.axis()的选项
| 参数 | 描述 |
|---|---|
| 空 | 返回当前轴限制 |
off |
关闭轴线和标签 |
equal |
导致等比例缩放 |
scaled |
通过尺寸变化实现等比例缩放 |
tight |
使所有数据可见(紧缩限制) |
image |
使所有数据可见(带有数据限制) |
[xmin, xmax, ymin, ymax] |
设置给定(列表的)值的限制 |
此外,您可以直接使用plt.xlim()和plt.ylim()设置每个轴的最小和最大值。以下代码提供了一个示例,其输出显示在图 7-5 中:
In [14]: plt.plot(y.cumsum())
plt.xlim(-1, 20)
plt.ylim(np.min(y.cumsum()) - 1,
np.max(y.cumsum()) + 1);
# plt.savefig('../../images/ch07/mpl_05')

图 7-5。带有自定义轴限制的图
为了更好地可读性,图表通常包含许多标签,例如标题和描述x和y值性质的标签。这些分别通过函数plt.title、plt.xlabel和plt.ylabel添加。默认情况下,plot绘制连续线条,即使提供了离散数据点。通过选择不同的样式选项来绘制离散点。图 7-6 叠加了(红色)点和(蓝色)线,线宽为 1.5 点:
In [15]: plt.figure(figsize=(10, 6)) 
plt.plot(y.cumsum(), 'b', lw=1.5) 
plt.plot(y.cumsum(), 'ro') 
plt.xlabel('index') 
plt.ylabel('value') 
plt.title('A Simple Plot'); 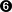
# plt.savefig('../../images/ch07/mpl_06')
增加图的大小。
将数据绘制为蓝色线条,线宽为 1.5 点。
将数据绘制为红色(粗)点。
在 x 轴上放置一个标签。
在 y 轴上放置一个标签。
放置一个标题。

图 7-6。具有典型标签的图
默认情况下,plt.plot()支持表 7-2 中的颜色缩写。
表 7-2。标准颜色缩写
| 字符 | 颜色 |
|---|---|
b |
蓝色 |
g |
绿色 |
r |
红色 |
c |
青色 |
m |
紫红色 |
y |
黄色 |
k |
黑色 |
w |
白色 |
在线和/或点样式方面,plt.plot()支持表 7-3 中列出的字符。
表 7-3. 标准样式字符
| 字符 | 符号 |
|---|---|
- |
实线型 |
-- |
虚线型 |
-. |
短划线-点线型 |
: |
点线型 |
. |
点标记 |
, |
像素标记 |
o |
圆形标记 |
v |
向下三角形标记 |
0 |
向上三角形标记 |
< |
向左三角形标记 |
> |
向右三角形标记 |
1 |
向下三角形标记 |
2 |
向上三角形标记 |
3 |
向左三角形标记 |
4 |
向右三角形标记 |
s |
正方形标记 |
p |
五边形标记 |
0 |
星形标记 |
h |
六边形 1 标记 |
H |
六边形 2 标记 |
0 |
加号标记 |
x |
X 标记 |
D |
菱形标记 |
d |
窄菱形标记 |
| `pass:[ | ]` |
| 垂直线标记 | 0 |
任何颜色缩写都可以与任何样式字符组合。通过这种方式,您可以确保不同的数据集易于区分。正如我们将看到的,绘图样式也将反映在图例中。
二维数据集
绘制一维数据可以被视为一种特殊情况。一般来说,数据集将由多个单独的数据子集组成。与 matplotlib 一维数据一样,处理这样的数据集遵循相同的规则。但是,在这种情况下可能会出现一些额外的问题。例如,两个数据集的缩放可能有如此之大的不同,以至于不能使用相同的 y 轴和/或 x 轴缩放绘制它们。另一个问题可能是您可能希望以不同的方式可视化两个不同的数据集,例如,通过线图绘制一个数据集,通过条形图绘制另一个数据集。
以下代码生成一个具有 20×2 形状的标准正态分布(伪随机)数字的NumPy ndarray对象的二维样本数据集。对这个数组,调用cumsum()方法来计算样本数据沿轴 0(即第一个维度)的累积和:
In [16]: y = np.random.standard_normal((20, 2)).cumsum(axis=0)
一般来说,您也可以将这样的二维数组传递给 plt.plot。然后,它将自动解释包含的数据为单独的数据集(沿着轴 1,即第二个维度)。相应的图示显示在图 7-7 中:
In [17]: plt.figure(figsize=(10, 6))
plt.plot(y, lw=1.5)
plt.plot(y, 'ro')
plt.xlabel('index')
plt.ylabel('value')
plt.title('A Simple Plot');
# plt.savefig('../../images/ch07/mpl_07')

图 7-7. 带有两个数据集的图
在这种情况下,进一步的注释可能有助于更好地阅读图表。您可以为每个数据集添加单独的标签,并在图例中列出它们。 plt.legend() 接受不同的位置参数。0 代表最佳位置,意味着图例尽可能少地遮挡数据。图 7-8 展示了两个数据集的图表,这次有了图例。在生成的代码中,我们现在不再将 ndarray 对象作为一个整体传递,而是分别访问两个数据子集(y[:, 0] 和 y[:, 0]),这样可以为它们附加单独的标签:
In [18]: plt.figure(figsize=(10, 6))
plt.plot(y[:, 0], lw=1.5, label='1st') 
plt.plot(y[:, 1], lw=1.5, label='2nd') 
plt.plot(y, 'ro')
plt.legend(loc=0) 
plt.xlabel('index')
plt.ylabel('value')
plt.title('A Simple Plot');
# plt.savefig('../../images/ch07/mpl_08')
为数据子集定义标签。
将图例放在最佳位置。
进一步的 plt.legend() 位置选项包括 表 7-4 中介绍的选项。
表 7-4. plt.legend() 的选项
| 位置 | 描述 |
|---|---|
| 空 | 自动 |
0 |
最佳位置 |
1 |
右上角 |
2 |
左上角 |
3 |
左下角 |
4 |
右下角 |
5 |
右 |
6 |
左中 |
7 |
右中 |
8 |
底部中心 |
9 |
上部中心 |
10 |
中心 |

图 7-8. 带标记数据集的图表
具有相似缩放的多个数据集,例如相同财务风险因素的模拟路径,可以使用单个 y 轴绘制。然而,通常数据集显示的缩放相差较大,并且使用单个 y 轴绘制此类数据通常会导致视觉信息的严重丢失。为了说明效果,我们将两个数据子集中的第一个缩放因子放大了 100 倍,并再次绘制数据(参见 图 7-9):
In [19]: y[:, 0] = y[:, 0] * 100 
In [20]: plt.figure(figsize=(10, 6))
plt.plot(y[:, 0], lw=1.5, label='1st')
plt.plot(y[:, 1], lw=1.5, label='2nd')
plt.plot(y, 'ro')
plt.legend(loc=0)
plt.xlabel('index')
plt.ylabel('value')
plt.title('A Simple Plot');
# plt.savefig('../../images/ch07/mpl_09')
重新调整第一个数据子集的比例。

图 7-9. 具有两个不同缩放数据集的图表
检查 图 7-9 发现,第一个数据集仍然“视觉可读”,而第二个数据集现在看起来像是直线,因为 y 轴的新缩放。在某种意义上,第二个数据集的信息现在“视觉上丢失了”。解决这个问题有两种基本方法:
-
使用两个 y 轴(左/右)
-
使用两个子图(上/下,左/右)
让我们先将第二个 y 轴引入图表中。图 7-10 现在有了两个不同的 y 轴。左侧的 y 轴用于第一个数据集,而右侧的 y 轴用于第二个数据集。因此,也有了两个图例:
In [21]: fig, ax1 = plt.subplots() 
plt.plot(y[:, 0], 'b', lw=1.5, label='1st')
plt.plot(y[:, 0], 'ro')
plt.legend(loc=8)
plt.xlabel('index')
plt.ylabel('value 1st')
plt.title('A Simple Plot')
ax2 = ax1.twinx() 
plt.plot(y[:, 1], 'g', lw=1.5, label='2nd')
plt.plot(y[:, 1], 'ro')
plt.legend(loc=0)
plt.ylabel('value 2nd');
# plt.savefig('../../images/ch07/mpl_10')
定义 figure 和 axis 对象。
创建共享 x 轴的第二个 axis 对象。

图 7-10. 具有两个数据集和两个 y 轴的图表
关键代码行是帮助管理坐标轴的代码行。这些是接下来的代码行:
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
通过使用 plt.subplots() 函数,我们直接访问基础绘图对象(图形、子图等)。例如,它允许生成一个共享 x 轴的第二个子图。在图 7-10 中,我们实际上有两个子图叠加在一起。
接下来,考虑两个分离子图的情况。这个选项给予了更多处理两个数据集的自由,就像图 7-11 所示:
In [22]: plt.figure(figsize=(10, 6))
plt.subplot(211) 
plt.plot(y[:, 0], lw=1.5, label='1st')
plt.plot(y[:, 0], 'ro')
plt.legend(loc=0)
plt.ylabel('value')
plt.title('A Simple Plot')
plt.subplot(212) 
plt.plot(y[:, 1], 'g', lw=1.5, label='2nd')
plt.plot(y[:, 1], 'ro')
plt.legend(loc=0)
plt.xlabel('index')
plt.ylabel('value');
# plt.savefig('../../images/ch07/mpl_11')
定义了上方子图 1。
定义了下方子图 2。

图 7-11. 具有两个子图的绘图
matplotlib figure 对象中子图的放置是通过使用特殊的坐标系统来完成的。plt.subplot() 接受三个整数作为参数,分别为 numrows、numcols 和 fignum(用逗号分隔或不分隔)。numrows 指定行的数量,numcols 指定列的数量,而 fignum 指定子图的数量,从 1 开始,以 numrows * numcols 结束。例如,具有九个等大小子图的图形将具有 numrows=3,numcols=3 和 fignum=1,2,...,9。右下方的子图将具有以下“坐标”:plt.subplot(3, 3, 9)。
有时,选择两种不同的图表类型来可视化这样的数据可能是必要的或者是期望的。通过子图的方法,您可以自由组合 matplotlib 提供的任意类型的图表。1 图 7-12 结合了线条/点图和柱状图:
In [23]: plt.figure(figsize=(10, 6))
plt.subplot(121)
plt.plot(y[:, 0], lw=1.5, label='1st')
plt.plot(y[:, 0], 'ro')
plt.legend(loc=0)
plt.xlabel('index')
plt.ylabel('value')
plt.title('1st Data Set')
plt.subplot(122)
plt.bar(np.arange(len(y)), y[:, 1], width=0.5,
color='g', label='2nd') 
plt.legend(loc=0)
plt.xlabel('index')
plt.title('2nd Data Set');
# plt.savefig('../../images/ch07/mpl_12')
创建一个 bar 子图。

图 7-12. 将线条/点子图与柱状子图组合的绘图
其他绘图样式
在二维绘图方面,线条和点图可能是金融中最重要的图表之一;这是因为许多数据集包含时间序列数据,通常通过这些图表进行可视化。第八章详细讨论了金融时间序列数据。然而,目前这一节还是采用了一个随机数的二维数据集,并且展示了一些备用的、对于金融应用有用的可视化方法。
第一种是散点图,其中一个数据集的值作为另一个数据集的x值。图 7-13 展示了这样一个图。例如,此类图用于绘制一个金融时间序列的回报与另一个金融时间序列的回报。对于此示例,我们将使用一个新的二维数据集以及一些更多的数据:
In [24]: y = np.random.standard_normal((1000, 2)) 
In [25]: plt.figure(figsize=(10, 6))
plt.plot(y[:, 0], y[:, 1], 'ro') 
plt.xlabel('1st')
plt.ylabel('2nd')
plt.title('Scatter Plot');
# plt.savefig('../../images/ch07/mpl_13')
创建一个包含随机数的较大数据集。
通过 plt.plot() 函数绘制散点图。

图 7-13. 通过 plot 函数绘制散点图
matplotlib 还提供了一个特定的函数来生成散点图。它基本上工作方式相同,但提供了一些额外的功能。图 7-14 展示了使用 plt.scatter() 函数生成的相应散点图,这次与 图 7-13 对应,:
In [26]: plt.figure(figsize=(10, 6))
plt.scatter(y[:, 0], y[:, 1], marker='o') 
plt.xlabel('1st')
plt.ylabel('2nd')
plt.title('Scatter Plot');
# plt.savefig('../../images/ch07/mpl_14')
通过 plt.scatter() 函数绘制的散点图。

图 7-14. 通过散点函数生成的散点图
例如,plt.scatter() 绘图函数允许添加第三个维度,可以通过不同的颜色来可视化,并且可以通过使用颜色条来描述。图 7-15 展示了一个散点图,其中第三个维度通过单个点的不同颜色来说明,并且有一个颜色条作为颜色的图例。为此,以下代码生成了一个具有随机数据的第三个数据集,这次是介于 0 到 10 之间的整数:
In [27]: c = np.random.randint(0, 10, len(y))
In [28]: plt.figure(figsize=(10, 6))
plt.scatter(y[:, 0], y[:, 1],
c=c, 
cmap='coolwarm', 
marker='o') 
plt.colorbar()
plt.xlabel('1st')
plt.ylabel('2nd')
plt.title('Scatter Plot');
# plt.savefig('../../images/ch07/mpl_15')
包含了第三个数据集。
选择了颜色映射。
将标记定义为粗点。

图 7-15. 具有第三维的散点图
另一种类型的图表,直方图,在金融收益的背景下也经常被使用。图 7-16 将两个数据集的频率值放在同一个图表中相邻位置:
In [29]: plt.figure(figsize=(10, 6))
plt.hist(y, label=['1st', '2nd'], bins=25) 
plt.legend(loc=0)
plt.xlabel('value')
plt.ylabel('frequency')
plt.title('Histogram');
# plt.savefig('../../images/ch07/mpl_16')
通过 plt.hist() 函数绘制直方图。

图 7-16. 两个数据集的直方图
由于直方图在金融应用中是如此重要的图表类型,让我们更近距离地看一下 plt.hist 的使用。以下示例说明了支持的参数:
plt.hist(x, bins=10, range=None, normed=False, weights=None, cumulative=False, bottom=None, histtype='bar', align='mid', orientation='vertical', rwidth=None, log=False, color=None, label=None, stacked=False, hold=None, **kwargs)
表 7-5 提供了 plt.hist 函数的主要参数的描述。
表 7-5. plt.hist() 的参数
| 参数 | 描述 |
|---|---|
x |
list 对象(s),ndarray 对象 |
bins |
柱子数量 |
range |
柱的下限和上限 |
normed |
规范化,使积分值为 1 |
weights |
x 中每个值的权重 |
cumulative |
每个柱包含低位柱的计数 |
histtype |
选项(字符串):bar,barstacked,step,stepfilled |
align |
选项(字符串):left,mid,right |
orientation |
选项(字符串):horizontal,vertical |
rwidth |
条柱的相对宽度 |
log |
对数刻度 |
color |
每个数据集的颜色(类似数组) |
label |
用于标签的字符串或字符串序列 |
stacked |
堆叠多个数据集 |
图 7-17 展示了类似的图表;这次,两个数据集的数据在直方图中堆叠:
In [30]: plt.figure(figsize=(10, 6))
plt.hist(y, label=['1st', '2nd'], color=['b', 'g'],
stacked=True, bins=20, alpha=0.5)
plt.legend(loc=0)
plt.xlabel('value')
plt.ylabel('frequency')
plt.title('Histogram');
# plt.savefig('../../images/ch07/mpl_17')

图 7-17. 两个数据集的堆叠直方图
另一种有用的绘图类型是箱线图。类似于直方图,箱线图既可以简明地概述数据集的特征,又可以轻松比较多个数据集。图 7-18 展示了我们数据集的这样一个图:
In [31]: fig, ax = plt.subplots(figsize=(10, 6))
plt.boxplot(y) 
plt.setp(ax, xticklabels=['1st', '2nd']) 
plt.xlabel('data set')
plt.ylabel('value')
plt.title('Boxplot');
# plt.savefig('../../images/ch07/mpl_18')
通过plt.boxplot()函数绘制箱线图。
设置各个 x 标签。
最后一个示例使用了函数plt.setp(),它为一个(组)绘图实例设置属性。例如,考虑由以下代码生成的线图:
line = plt.plot(data, 'r')
下面的代码:
plt.setp(line, linestyle='--')
将线条样式更改为“虚线”。这样,您可以在生成绘图实例(“艺术家对象”)之后轻松更改参数。

图 7-18. 两个数据集的箱线图
作为本节的最后一个示例,请考虑一个在matplotlib 画廊中也可以找到的受数学启发的绘图。它绘制了一个函数并在图形上突出显示了函数下方的区域,从下限到上限 — 换句话说,函数在下限和上限之间的积分值突出显示为一个区域。要说明的积分值是,其中,,。图 7-19 显示了结果图,并演示了matplotlib如何无缝处理数学公式的LaTeX类型设置以将其包含到绘图中。首先,函数定义,积分限制作为变量以及 x 和 y 值的数据集。
In [32]: def func(x):
return 0.5 * np.exp(x) + 1 
a, b = 0.5, 1.5 
x = np.linspace(0, 2) 
y = func(x) 
Ix = np.linspace(a, b) 
Iy = func(Ix) 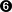
verts = [(a, 0)] + list(zip(Ix, Iy)) + [(b, 0)] 
函数定义。
积分限制。
用于绘制函数的 x 值。
用于绘制函数的 y 值。
积分限制内的 x 值。
积分限制内的 y 值。
包含多个表示要绘制的多边形的坐标的list对象。
其次,由于需要明确放置许多单个对象,绘图本身有点复杂。
In [33]: from matplotlib.patches import Polygon
fig, ax = plt.subplots(figsize=(10, 6))
plt.plot(x, y, 'b', linewidth=2) 
plt.ylim(ymin=0) 
poly = Polygon(verts, facecolor='0.7', edgecolor='0.5') 
ax.add_patch(poly) 
plt.text(0.5 * (a + b), 1, r'$\int_a^b f(x)\mathrm{d}x$',
horizontalalignment='center', fontsize=20) 
plt.figtext(0.9, 0.075, '$x$') 
plt.figtext(0.075, 0.9, '$f(x)$') 
ax.set_xticks((a, b)) 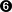
ax.set_xticklabels(('$a$', '$b$')) 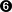
ax.set_yticks([func(a), func(b)]) 
ax.set_yticklabels(('$f(a)$', '$f(b)$')) 
# plt.savefig('../../images/ch07/mpl_19')
Out[33]: [<matplotlib.text.Text at 0x1066af438>, <matplotlib.text.Text at 0x10669ba20>]
将函数值绘制为蓝线。
定义纵坐标轴的最小 y 值。
以灰色绘制多边形(积分区域)。
将积分公式放置在图中。
放置轴标签。
放置 x 标签。
放置 y 标签。

图 7-19。指数函数、积分区域和 LaTeX 标签
静态 3D 绘图
在金融领域,确实没有太多领域真正受益于三维可视化。然而,一个应用领域是同时显示一系列到期时间和行权价的隐含波动率的波动率曲面。接下来,代码人工生成类似于波动率曲面的图形。为此,请考虑:
-
50 到 150 之间的行权价值
-
0.5 到 2.5 年的到期时间
这提供了一个二维坐标系。NumPy的np.meshgrid()函数可以从两个一维ndarray对象生成这样的系统:
In [34]: strike = np.linspace(50, 150, 24) 
In [35]: ttm = np.linspace(0.5, 2.5, 24) 
In [36]: strike, ttm = np.meshgrid(strike, ttm) 
In [37]: strike[:2].round(1) 
Out[37]: array([[ 50. , 54.3, 58.7, 63. , 67.4, 71.7, 76.1, 80.4, 84.8,
89.1, 93.5, 97.8, 102.2, 106.5, 110.9, 115.2, 119.6, 123.9,
128.3, 132.6, 137. , 141.3, 145.7, 150. ],
[ 50. , 54.3, 58.7, 63. , 67.4, 71.7, 76.1, 80.4, 84.8,
89.1, 93.5, 97.8, 102.2, 106.5, 110.9, 115.2, 119.6, 123.9,
128.3, 132.6, 137. , 141.3, 145.7, 150. ]])
In [38]: iv = (strike - 100) ** 2 / (100 * strike) / ttm 
In [39]: iv[:5, :3] 
Out[39]: array([[1. , 0.76695652, 0.58132045],
[0.85185185, 0.65333333, 0.4951989 ],
[0.74193548, 0.56903226, 0.43130227],
[0.65714286, 0.504 , 0.38201058],
[0.58974359, 0.45230769, 0.34283001]])
ndarray对象中的行权价值。
ndarray 对象中的时间至到期值。
创建的两个二维ndarray对象(网格)。
虚拟的隐含波动率值。
由以下代码生成的图形显示在图 7-20 中:
In [40]: from mpl_toolkits.mplot3d import Axes3D 
fig = plt.figure(figsize=(10, 6))
ax = fig.gca(projection='3d') 
surf = ax.plot_surface(strike, ttm, iv, rstride=2, cstride=2,
cmap=plt.cm.coolwarm, linewidth=0.5,
antialiased=True) 
ax.set_xlabel('strike') 
ax.set_ylabel('time-to-maturity') 
ax.set_zlabel('implied volatility') 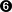
fig.colorbar(surf, shrink=0.5, aspect=5); 
# plt.savefig('../../images/ch07/mpl_20')
导入相关的 3D 绘图特性。
为 3D 绘图设置画布。
创建 3D 图。
设置 x 标签。
设置 y 标签。
设置 z 标签。
这将创建一个色标。

图 7-20。 (虚拟) 隐含波动率的三维曲面图
表 7-6 提供了plt.plot_surface()函数可以接受的不同参数的描述。
表 7-6。plot_surface的参数
| 参数 | 描述 |
|---|---|
X, Y, Z |
数据值为 2D 数组 |
rstride |
数组行跨度(步长) |
cstride |
数组列跨度(步长) |
color |
表面补丁的颜色 |
cmap |
表面补丁的颜色映射 |
facecolors |
各个补丁的面颜色 |
norm |
用于将值映射到颜色的 Normalize 的实例 |
vmin |
要映射的最小值 |
vmax |
要映射的最大值 |
shade |
是否着色面颜色 |
与二维图相似,线型可以由单个点或如下所示的单个三角形替代。图 7-21 将相同的数据绘制为 3D 散点图,但现在还使用 view_init() 方法设置了不同的视角:
In [41]: fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111, projection='3d')
ax.view_init(30, 60) 
ax.scatter(strike, ttm, iv, zdir='z', s=25,
c='b', marker='^') 
ax.set_xlabel('strike')
ax.set_ylabel('time-to-maturity')
ax.set_zlabel('implied volatility');
# plt.savefig('../../images/ch07/mpl_21')
设置视角。
创建 3D 散点图。

图 7-21. (虚拟的) 隐含波动率的 3D 散点图
交互式 2D 绘图
matplotlib 允许创建静态位图对象或 PDF 格式的绘图。如今,有许多可用于基于 D3.js 标准创建交互式绘图的库。这些绘图可以实现缩放和悬停效果以进行数据检查,还可以轻松嵌入到网页中。
一个流行的平台和绘图库是Plotly。它专门用于数据科学的可视化,并在全球范围内广泛使用。Plotly 的主要优点是其与 Python 生态系统的紧密集成以及易于使用 — 特别是与 pandas 的 DataFrame 对象和包装器包 Cufflinks 结合使用时。
对于某些功能,需要使用 Plotly 的免费帐户,用户可以在平台本身 http://plot.ly 下注册。一旦授予凭据,它们应该被本地存储以供以后永久使用。所有相关详细信息都在使用 Plotly for Python 入门 中找到。
本节仅关注选定的方面,因为 Cufflinks 专门用于从存储在 DataFrame 对象中的数据创建交互式绘图。
基本绘图
要从 Jupyter Notebook 上下文开始,需要一些导入,并且应该打开 notebook 模式。
In [42]: import pandas as pd
In [43]: import cufflinks as cf 
In [44]: import plotly.offline as plyo 
In [45]: plyo.init_notebook_mode(connected=True) 
导入 Cufflinks。
导入 Plotly 的离线绘图功能。
打开笔记本绘图模式。
提示
使用Plotly,还可以选择在Plotly服务器上呈现绘图。然而,笔记本模式通常更快,特别是处理较大数据集时。但是,像Plotly的流图服务之类的一些功能仅通过与服务器通信才可用。
后续示例再次依赖随机数,这次存储在具有DatetimeIndex的DataFrame对象中,即作为时间序列数据。
In [46]: a = np.random.standard_normal((250, 5)).cumsum(axis=0) 
In [47]: index = pd.date_range('2019-1-1', 
freq='B', 
periods=len(a)) 
In [48]: df = pd.DataFrame(100 + 5 * a, 
columns=list('abcde'), 
index=index) 
In [49]: df.head() 
Out[49]: a b c d e
2019-01-01 109.037535 98.693865 104.474094 96.878857 100.621936
2019-01-02 107.598242 97.005738 106.789189 97.966552 100.175313
2019-01-03 101.639668 100.332253 103.183500 99.747869 107.902901
2019-01-04 98.500363 101.208283 100.966242 94.023898 104.387256
2019-01-07 93.941632 103.319168 105.674012 95.891062 86.547934
标准正态分布的(伪)随机数。
DatetimeIndex对象的开始日期。
频率(“business daily“)。
所需周期数。
原始数据进行线性转换。
将列标题作为单个字符。
DatetimeIndex对象。
前五行的数据。
Cufflinks为DataFrame类添加了一个新方法:df.iplot()。此方法在后台使用Plotly创建交互式图。本节中的代码示例都利用了将交互式图下载为静态位图的选项,然后将其嵌入到文本中。在 Jupyter Notebook 环境中,创建的绘图都是交互式的。下面代码的结果显示为<<>>。
In [50]: plyo.iplot( 
df.iplot(asFigure=True), 
# image ='png', 
filename='ply_01' 
)
这利用了Plotly的离线(笔记本模式)功能。
使用参数asFigure=True调用df.iplot()方法以允许本地绘图和嵌入。
image选项还提供了绘图的静态位图版本。
指定要保存的位图的文件名(文件类型扩展名会自动添加)。

图 7-22. 使用Plotly、pandas和Cufflinks绘制时间序列数据的线图
与matplotlib一般或pandas绘图功能一样,可用于自定义此类绘图的多个参数(参见图 7-23):
In [51]: plyo.iplot(
df[['a', 'b']].iplot(asFigure=True,
theme='polar', 
title='A Time Series Plot', 
xTitle='date', 
yTitle='value', 
mode={'a': 'markers', 'b': 'lines+markers'}, 
symbol={'a': 'dot', 'b': 'diamond'}, 
size=3.5, 
colors={'a': 'blue', 'b': 'magenta'}, 
),
# image ='png',
filename='ply_02'
)
选择绘图的主题(绘图样式)。
添加标题。
添加 x 标签。
添加 y 标签。
按列定义绘图模式(线条、标记等)。
按列定义要用作标记的符号。
为所有标记固定大小。
按列指定绘图颜色

图 7-23. DataFrame 对象的两列线图及自定义
与 matplotlib 类似,Plotly 允许使用多种不同的绘图类型。通过 Cufflinks 可用的绘图有:chart, scatter, bar, box, spread, ratio, heatmap, surface, histogram, bubble, bubble3d, scatter3d, scattergeo, ohlc, candle, pie 和 choroplet。作为与线图不同的绘图类型的示例,请考虑直方图(参见[链接即将到来]):
In [52]: plyo.iplot(
df.iplot(kind='hist', 
subplots=True, 
bins=15, 
asFigure=True),
# image ='png',
filename='ply_03'
)
指定绘图类型。
每列需要单独的子图。
设置 bins 参数(要使用的桶=要绘制的条形图)。

图 7-24. DataFrame 对象的每列直方图
金融图表
当处理金融时间序列数据时,Ploty、Cufflinks 和 pandas 的组合特别强大。Cufflinks 提供了专门的功能,用于创建典型的金融图,并添加典型的金融图表元素,例如相对强度指标(RSI),这只是一个例子。为此,创建了一个持久的 QuantFig 对象,可以像使用 Cufflinks 的 DataFrame 对象一样绘制。
此子部分使用真实的金融数据集:欧元/美元汇率的时间序列数据(来源:FXCM Forex Capital Markets Ltd.)。
In [53]: # data from FXCM Forex Capital Markets Ltd.
raw = pd.read_csv('../../source/fxcm_eur_usd_eod_data.csv',
index_col=0, parse_dates=True) 
In [54]: raw.info() 
<class 'pandas.core.frame.DataFrame'>
DatetimeIndex: 2820 entries, 2007-06-03 to 2017-05-31
Data columns (total 10 columns):
Time 2820 non-null object
OpenBid 2820 non-null float64
HighBid 2820 non-null float64
LowBid 2820 non-null float64
CloseBid 2820 non-null float64
OpenAsk 2820 non-null float64
HighAsk 2820 non-null float64
LowAsk 2820 non-null float64
CloseAsk 2820 non-null float64
TotalTicks 2820 non-null int64
dtypes: float64(8), int64(1), object(1)
memory usage: 242.3+ KB
In [55]: quotes = raw[['OpenAsk', 'HighAsk', 'LowAsk', 'CloseAsk']] 
quotes = quotes.iloc[-60:] 
quotes.tail() 
Out[55]: OpenAsk HighAsk LowAsk CloseAsk
Date
2017-05-27 1.11808 1.11808 1.11743 1.11788
2017-05-28 1.11788 1.11906 1.11626 1.11660
2017-05-29 1.11660 1.12064 1.11100 1.11882
2017-05-30 1.11882 1.12530 1.11651 1.12434
2017-05-31 1.12434 1.12574 1.12027 1.12133
从逗号分隔值(CSV)文件中读取财务数据。
结果 DataFrame 对象包含多列和超过 2,800 行数据。
从 DataFrame 对象中选择四列(开-高-低-收)。
仅用于可视化的少量数据行。
结果数据集 quotes 的最后五行。
在实例化期间,QuantFig 对象将 DataFrame 对象作为输入,并允许进行一些基本的自定义。然后使用 qf.iplot() 方法绘制存储在 QuantFig 对象 qf 中的数据(参见图 7-25)。
In [56]: qf = cf.QuantFig(
quotes, 
title='EUR/USD Exchange Rate', 
legend='top', 
name='EUR/USD' 
)
In [57]: plyo.iplot(
qf.iplot(asFigure=True),
# image ='png',
filename='qf_01'
)
DataFrame 对象传递给 QuantFig 构造函数。
添加图标题。
图例放置在图的顶部。
这给数据集起了个名字。

图 7-25. EUR/USD 数据的 OHLC 图
添加典型的金融图表元素,如 Bollinger 带,通过 QuantFig 对象的不同可用方法进行 (见图 7-26)。
In [58]: qf.add_bollinger_bands(periods=15, 
boll_std=2) 
In [59]: plyo.iplot(qf.iplot(asFigure=True),
# image='png',
filename='qf_02')
Bollinger 带的周期数。
用于带宽的标准偏差数。

图 7-26. EUR/USD 数据的 OHLC 图,带有 Bollinger 带
添加了某些金融指标,如 RSI,作为一个子图 (见图 7-27)。
In [60]: qf.add_rsi(periods=14, 
showbands=False) 
In [61]: plyo.iplot(
qf.iplot(asFigure=True),
# image='png',
filename='qf_03'
)
修复了 RSI 周期。
不显示上限或下限带。

图 7-27. EUR/USD 数据的 OHLC 图,带有 Bollinger 带和 RSI
结论
当涉及到 Python 中的数据可视化时,matplotlib 可以被认为是基准和工作马。它与 NumPy 和 pandas 紧密集成。基本功能易于方便地访问。然而,另一方面,matplotlib 是一个相当强大的库,具有一种相对复杂的 API。这使得在本章中无法对 matplotlib 的所有功能进行更广泛的概述。
本章介绍了在许多金融背景下有用的 matplotlib 的 2D 和 3D 绘图的基本功能。其他章节提供了如何在可视化中使用这个基本库的更多示例。
除了 matplotlib,本章还涵盖了 Plotly 与 Cufflinks 的组合。这种组合使得创建交互式 D3.js 图表成为一件方便的事情,因为通常只需在 DataFrame 对象上进行一次方法调用。所有的技术细节都在后端处理。此外,Cufflinks 通过 QuantFig 对象提供了一种创建带有流行金融指标的典型金融图表的简单方法。
进一步阅读
matplotlib 的主要资源可以在网络上找到:
-
matplotlib的主页,当然,是最好的起点:http://matplotlib.org。 -
有许多有用示例的画廊:http://matplotlib.org/gallery.html。
-
一个用于 2D 绘图的教程在这里:http://matplotlib.org/users/pyplot_tutorial.html。
-
另一个用于 3D 绘图的是:http://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html。
现在已经成为一种标准的例程去参考画廊,寻找合适的可视化示例,并从相应的示例代码开始。
Plotly 和 Cufflinks 的主要资源也可以在线找到:
-
matplotlib的主页:http://matplotlib.org -
一个 Python 入门教程:https://plot.ly/python/getting-started/
-
Cufflinks的 Github 页面:https://github.com/santosjorge/cufflinks
¹ 想了解可用的绘图类型概述,请访问matplotlib gallery。




























































































































































































