题目:打印int类型整数的32位信息
1与任何二进制的与运算:同1为1,有0为0;可以让整数每一位和1做与运算,按位输出结果
这是循环的操作,并且应该从最高位 32位按位输出,也就是最开始1应该左移31位,接下来左移30位
public class Code01_PrintBinary {
public static void printBinary(int num){
for (int i = 31; i >= 0; i--) {
System.out.print((num & (1 << i)) == 0 ? "0" : "1");
}
System.out.println();
}
public static void main(String[] args) {
int num = 2147483647;
printBinary(num);
}
}
一个数字左移一位,就是这个数字乘了2
int类型是32位,如果是无符号整型的表示范围是0 ~ 2^32 - 1 , 但是为了表示负数,实际的范围是
-2^31 ~ 2^31 - 1,0归属在了非负区域,所以正数比负数少了一个
右移
右移分为 带符号右移 和 无符号右移
- 带符号右移 >>
printBinary(-1024 >> 1); //11111111111111111111111000000000
右移一位,左边用符号位补齐
- 无符号右移 >>>
printBinary(-1024 >>> 1); //01111111111111111111111000000000
右移一位,左边用0补齐
题目:计算一个数的相反数
正数 按位取反 加1 就得到了这个数对应的负数
int c = 5;
int d = -c; //相反数
d = (~c + 1); //相反数
/**
5 的二进制 : 00000000000000000000000000000101
~ 取反: 11111111111111111111111111111010
+1 : 11111111111111111111111111111011
*/
这样设计的好处是,底层对于两个数的加法都可以通过一套逻辑实现
任何正数的相反数都有负数对应,负数最小值取相反数是哪个数对应呢?
System.out.println(~Integer.MIN_VALUE + 1);//-2147483648
负数最小值是 10000000000000000000000000000000
取反 01111111111111111111111111111111
+1 10000000000000000000000000000000
算法
算法是对一个问题的具体流程,并且具有评价处理流程的可量化指标
算法分为两类:
- 知道怎么算的算法
- 知道怎么试的算法
题目:给定一个参数N,计算1! + 2! + 3! + ... + N!
算法1:每个阶乘都计算再相加
算法2:2! 就是 1! * 2 ,3! 就是 2! * 3 ,4! 就是 3! * 4
常数操作
常数操作即固定时间的操作,加减乘除的操作都是固定时间的操作,1 + 1和 10000 + 10000 的执行时间应该是相同的,底层都是32位二进制的加法操作;数组寻址操作也是固定时间的操作。
- 算术运算
- 位运算
- 赋值、比较、自增自减
- 数组寻址
对于打印链表的操作来说:
查看该节点是否为空 O(1)
打印 O(1)
寻址下一节点 O(1)
遍历N次,总的时间复杂度就是O(N)
但是如果代码这样写:
for(int i = 0; i < list.size(); i++){
int num = list.get(i);
syso(num);
}
get(i) 就是时间复杂度O(N)的操作,整个for循环就是O(N^2)的操作。
重点:对于使用的每一个API都要非常熟悉
时间复杂度
O(?) ,在数据量为N的样本中,执行完整个流程的常数操作的数量关系。
分析时间复杂度的前提:将算法流程中每一步分解为常数时间的操作
选择排序的步骤:
- a. N个数看一遍,找到最小值,常数操作:看N次,比较N次,共2N
b. 最小值放在0位置,O(1) 一次交换 - a. 1 ~ (N - 1)看一次,找到最小值
b. 最小值放在1位置,O(1)
第一次在N个数之间进行看 + 比较,第二次在N - 1个数之间进行看 + 比较
也可以这样估算:
第一次在N个数之间进行常数操作
第二次在N - 1个数之间进行常数操作
最后在2个数之间进行常数操作
等差数列求和得到结果的最高阶必定是O(n^2)
时间频度
一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费的时间也越多。一个算法中的语句执行次数称为语句频度或时间频度,记为T(n)。
计算以下代码的时间频度T(n)
public void test(int n) {
int sum = 0;
for(int i = 0; i < n; i++) {
sum += i;
}
}
在时间频度T(n)中,n是问题的规模,当n不断变化时,时间频度T(n)也会不断变化。如果我们想知道时间频度的变化呈现什么规律,就引入了时间复杂度的概念。
时间复杂度的定义
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同量级函数。记作T(n)=O(f(n)),也称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。
时间复杂度的计算步骤
- 计算基本操作的执行次数T(n)
在做算法分析时,一般默认考虑最坏的情况。
- 计算T(n)的数量级f(n)
求T(n)的数量级f(n),只需要将T(n)做两个操作:
(一)忽略常数项、低次幂项和最高次幂项的系数。
(二)f(n)=(T(n)的数量级)。例如,在T(n)=4n2+2n+2中,T(n)的数量级函数f(n)=n2。
计算T(n)的数量级f(n),我们只要保证T(n)中的最高次幂正确即可,可以忽略所有常数项、低次幂项和最高次幂的系数。这样能够简化算法分析,将注意力集中在最重要的一点上:增长率。
- 用大O表示时间复杂度
当n趋近于无穷大时,如果T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))。例如,在T(n)=4n2+2n+2中,就有f(n)=n2,使得T(n)/f(n)的极限值为4,也就是得到时间复杂度为O(n^2)。
切记,时间频度不相同时,但是时间复杂度有可能相同,如T(n)=n2+3n+4与T(n)=4n2+2n+1它们的时间频度不同,但时间复杂度相同,都为O(n^2)。
常见的时间复杂度
常见的时间复杂度有:常数阶O(1),对数阶O(log2n),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n2),立方阶O(n3),指数阶O(2^n)和阶乘阶O(n!)。
常数阶 O(1)
无论代码执行了多少行,只要没有循环等复杂结构,那这个代码的时间复杂度就都是O(1)。
int num1 = 3, num2 = 5;
int temp = num1;
num1 = num2;
num2 = temp;
System.out.println("num1:" + num1 + " num2:" + num2);
在上述代码中,没有循环等复杂结构,它消耗的时间并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度。
对数阶 O(log2n)
O(log2n)指的就是:在循环中,每趟循环执行完毕后,循环变量都放大两倍。
int n = 1024;
for(int i = 1; i < n; i *= 2) {
System.out.println("hello powernode");
}
推算过程:假设该循环的执行次数为x次(也就是i的取值为2x),就满足了循环的结束条件,即满足了2x等于n,通过数学公式转换后,即得到了x = log2n,也就是说最多循环log2n次以后,这个代码就结束了,因此这个代码的时间复杂度为:O(log2n) 。
同理,如果每趟循环执行完毕后,循环变量都放大3倍,那么时间复杂度就为:O(log3n) 。
线性阶 O(n)
int n = 100;
for(int i = 0; i < n; i++) {
System.out.println("hello powernode");
}
在上述代码中,for循环会执行n趟,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
线性对数阶 O(nlog2n)
int n = 100;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j *= 2) {
System.out.println("hello powernode");
}
}
线性对数阶O(nlog2n) 其实非常容易理解,将时间复杂度为O(log2n)的代码循环n遍的话,那么它的时间复杂度就是n* O(log2n),也就是了O(nlog2n)。
平方阶 O(n^2)
int n = 100;
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
System.out.println("hello powernode");
}
}
外层i的循环执行一次,内层j的循环就要执行n次。因为外层执行n次,那么总的就需要执行n* n次,也就是需要执行n2次。因此这个代码的时间复杂度为:O(n2)。
平方阶的另外一个例子:
int n = 100;
for(int i = 1; i <= n; i++) {
for(int j = i; j <= n; j++) {
System.out.println("hello powernode");
}
}
i=1的时候,内侧循环执行n次,当i=2的时候,内侧循环执行(n-1)次,......一直这样子下去就可以构造出一个等差数列:n+(n-1)+(n-2)+......+2+1 ≈ (n2)/2。根据大O表示法,去掉最高次幂的系数,就可以得到时间复杂度为:O(n2)。
同理,立方阶 O(n3),参考上面的O(n2)去理解,也就是需要用到3层循环。
指数阶O(2^n)和阶乘阶O(n!)
指数阶O(2n)指的就是:当n为10的时候,需要执行210次。
阶乘阶O(n!)指的就是:当n为10的时候,需要执行10* 9* 8...2*1次。
常见的时间复杂度耗时比较
算法的时间复杂度是衡量一个算法好坏的重要指标。一般情况下,随着规模n的增大,T(n)的增长较慢的算法为最优算法。
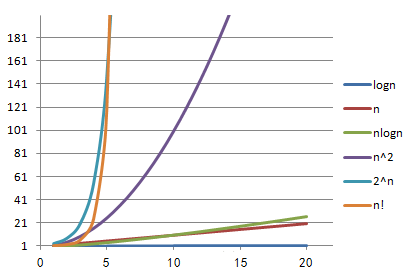
其中x轴代表n值,y轴代表T(n)值。T(n)值随着n的值的变化而变化,其中可以看出O(n!)和O(2n)随着n值的增大,它们的T(n)值上升幅度非常大,而O(logn)、O(n)、O(nlogn)、O(n2)随着n值的增大,T(n)值上升幅度相对较小。
常用的时间复杂度按照耗费的时间从小到大依次是:O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!)。
选择排序
public static void selectionSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
/**
* 0 ~ N - 1 找到最小值,放在第 0个位置上
* 1 ~ N - 1 找到最小值,放在第 1个位置上
* 2 ~ N - 1 找到最小值,放在第 2个位置上
* 第一个循环控制
*/
for (int i = 0; i < arr.length; i++) {
int minIdx = i;
for (int j = i; j < arr.length; j++) {
/*从i开始,向后遍历找到最小值*/
minIdx = arr[j] < arr[minIdx] ? j : minIdx;
}
swap(arr, i, minIdx);
}
}
private static void swap(int[] arr, int i, int minIdx) {
int temp = arr[i];
arr[i] = arr[minIdx];
arr[minIdx] = temp;
}
冒泡排序
N个数之间相邻两数谁大谁向右,直到2个数之间谁大谁往右,一共是O(N^2)
public static void bubbleSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
for (int i = arr.length - 1; i >= 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]){
swap(arr,j,j + 1);
}
}
System.out.println(Arrays.toString(arr));
}
}
private static void swap(int[] arr, int i, int minIdx) {
int temp = arr[i];
arr[i] = arr[minIdx];
arr[minIdx] = temp;
}
插入排序
- 0 ~ 0 位置有序
- 0 ~ 1 位置有序
- 0 ~ 2 位置有序
- 0 ~ 3 位置有序
- 0 ~ N - 1 位置有序
如果0 - 2已经有序了,在对0 - 3进行排序的时候仅仅需要将2与3位置比较,如果需要交换在向前比较
如果在某一轮的第一次比较时不需要交换,这一轮都不需要交换了。
对于插入排序来说,似乎时间复杂度无法估计:
- 对于有序的情况,是O(N)
- 对于完全逆序的情况,是O(N^2)
如果一个流程是会随着样本集变化的,时间复杂度就是最坏的情况
public static void insertionSort(int[] arr){
if (arr == null || arr.length < 2){
return;
}
/**
* 0 - 0 有序
* 0 - 1 有序
* 0 - 2 有序
* 0 - 3 有序
* 0 - i 有序
* 0 - N-1 有序
*/
for (int i = 1; i < arr.length; i++) {
//直到左边没有数 或者 左边的数小于右边的数 就停
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--){
swap(arr,j,j + 1);
}
}
}
private static void swap(int[] arr, int i, int minIdx) {
int temp = arr[i];
arr[i] = arr[minIdx];
arr[minIdx] = temp;
}
与冒泡排序差距很大,样本集对冒泡排序的效率影响较低,都是N^2,即使在优良的数据状况下效率的改变也微乎其微(仅仅省略了交换);而插入排序在优良的时间复杂度下效率很好
额外的空间复杂度
用户的输入 和 用户期待的结果 都不算额外的空间,程序为了实现这个功能所使用的空间是额外空间。
如果用户输入一个数组,期待返回一个拷贝后的数组,那么正常情况下程序的额外空间复杂度就是O1
但如果在程序设计的过程中使用到了其他的数组或集合,额外空间复杂度就是ON
常数时间
如果在两个时间复杂度相同的算法中选择,就需要放弃理论,使用随机的大样本量进行比较
例如:+运算的效率没有^运算高,即便都是常数操作
最优解
完成题目要求的时间复杂度尽可能低,空间再尽可能去优化(但是不包含常数级优化)
常见时间复杂度排名
1
logN
N
N * logN
N^2
N^3
N^k
2^N
3^N
k^N
N!
k为常数
int tmp;
tmp = a;
a = b;
b = tmp;
movl b, %eax ;将b从内存载入到寄存器eax
movl a, %edx ;将a从内存载入到寄存器edx
movl %eax, a ;将eax的内容存入到内存a中
xorl %eax, %eax ;将eax清零
movl %edx, b ;将edx的内容存入到内存b中
a ^= b;
b ^= a;
a ^= b;
movl b, %eax ;将b从内存载入寄存器eax
movl a, %ecx ;将a从内存载入寄存器ecx
movl %eax, %edx ;将eax的值保存到edx中
xorl %ecx, %edx ;ecx与edx异或
xorl %edx, %eax ;edx与eax异或
xorl %eax, %edx ;eax与edx异或
movl %eax, b ;将eax的值存入到内存b中
xorl %eax, %eax ;将eax置0:设置返回值,与上例中一样
movl %edx, a ;将edx的值存入到内存a中