【二】栈
【0】引入

-
栈如同叠猫猫,而队列就像猫猫排队。
-
两者分别代表着先入后出和先入先出的逻辑关系。
【1】栈的介绍
- 「栈 stack」是一种遵循先入后出的逻辑的线性数据结构。
- 我们可以将栈类比为桌面上的一摞盘子,如果需要拿出底部的盘子,则需要先将上面的盘子依次取出。
- 我们将盘子替换为各种类型的元素(如整数、字符、对象等),就得到了栈数据结构。
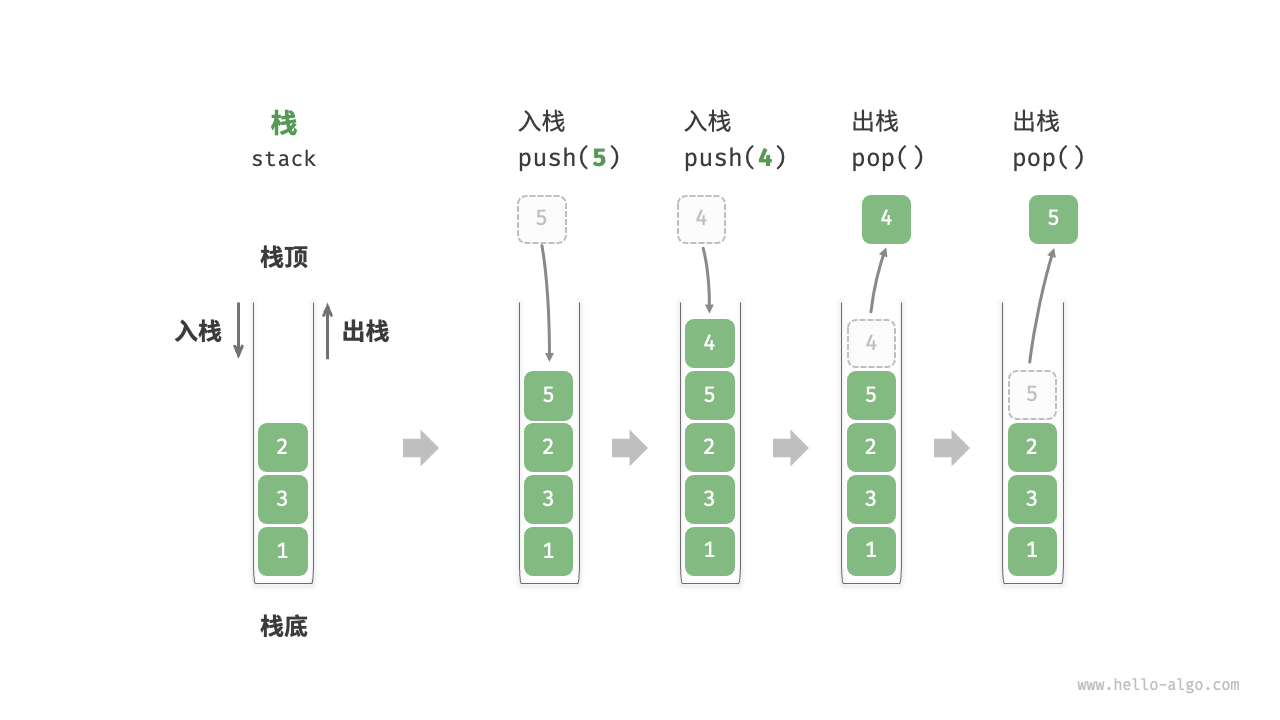
- 如图 5-1 所示,我们把堆叠元素的顶部称为“栈顶”,底部称为“栈底”。
- 将把元素添加到栈顶的操作叫做“入栈”,删除栈顶元素的操作叫做“出栈”。
【2】栈的实现
- 栈遵循先入后出的原则,因此我们只能在栈顶添加或删除元素。
- 然而,数组和链表都可以在任意位置添加和删除元素,因此栈可以被视为一种受限制的数组或链表。
- 换句话说,我们可以“屏蔽”数组或链表的部分无关操作,使其对外表现的逻辑符合栈的特性。
【3】基于链表的实现
- 使用链表来实现栈时,我们可以将链表的头节点视为栈顶,尾节点视为栈底。
- 如图 5-2 所示,对于入栈操作,我们只需将元素插入链表头部,这种节点插入方法被称为“头插法”。
- 而对于出栈操作,只需将头节点从链表中删除即可。
(1)基于链表图解
- LinkedListStack

- push()

- pop()

(2)基于链表代码
class LinkedListStack:
"""基于链表实现的栈"""
def __init__(self):
"""构造方法"""
self._peek: ListNode | None = None
self._size: int = 0
def size(self) -> int:
"""获取栈的长度"""
return self._size
def is_empty(self) -> bool:
"""判断栈是否为空"""
return not self._peek
def push(self, val: int):
"""入栈"""
node = ListNode(val)
node.next = self._peek
self._peek = node
self._size += 1
def pop(self) -> int:
"""出栈"""
num = self.peek()
self._peek = self._peek.next
self._size -= 1
return num
def peek(self) -> int:
"""访问栈顶元素"""
if self.is_empty():
raise IndexError("栈为空")
return self._peek.val
def to_list(self) -> list[int]:
"""转化为列表用于打印"""
arr = []
node = self._peek
while node:
arr.append(node.val)
node = node.next
arr.reverse()
return arr
【4】基于数组的实现
- 使用数组实现栈时,我们可以将数组的尾部作为栈顶。
- 如图 5-3 所示,入栈与出栈操作分别对应在数组尾部添加元素与删除元素
(1)基于数组图解
- ArrayStack

- push()

- pop()

(2)基于数组代码
- 由于入栈的元素可能会源源不断地增加,因此我们可以使用动态数组,这样就无须自行处理数组扩容问题。
class ArrayStack:
"""基于数组实现的栈"""
def __init__(self):
"""构造方法"""
self._stack: list[int] = []
def size(self) -> int:
"""获取栈的长度"""
return len(self._stack)
def is_empty(self) -> bool:
"""判断栈是否为空"""
return self._stack == []
def push(self, item: int):
"""入栈"""
self._stack.append(item)
def pop(self) -> int:
"""出栈"""
if self.is_empty():
raise IndexError("栈为空")
return self._stack.pop()
def peek(self) -> int:
"""访问栈顶元素"""
if self.is_empty():
raise IndexError("栈为空")
return self._stack[-1]
def to_list(self) -> list[int]:
"""返回列表用于打印"""
return self._stack
【5】栈典型应用
- 浏览器中的后退与前进、软件中的撤销与反撤销。每当我们打开新的网页,浏览器就会将上一个网页执行入栈,这样我们就可以通过后退操作回到上一页面。后退操作实际上是在执行出栈。如果要同时支持后退和前进,那么需要两个栈来配合实现。
- 程序内存管理。每次调用函数时,系统都会在栈顶添加一个栈帧,用于记录函数的上下文信息。在递归函数中,向下递推阶段会不断执行入栈操作,而向上回溯阶段则会执行出栈操作。