算法实验报告1
发布地址(方便阅读):
P183习题-T1
题目描述
给定一个数字n和子集1,2,3,...,n - 1,请用数组输出所有不同的划分方式。
4有四种划分方式:1+1+1+11+1+2.1+3.2+2.5有六种划分方式:1+1+1+1+1.1+1+1+2,1+1+3,1+2+2,1+4,3+2。给定一个数字n和子集1,2,3.…,n-1,请用数组输出所有不同的划分方式。例如:
输入:4
输出:[(1,1,1,1),(1,1,2),(1,3),(2,2]]
题目解析
使用 DFS 来找到所有可能的整数划分。
-
如果
n变为0,这意味着当前的cur数组是N的一个有效划分,因为加起来正好等于N。将这个划分作为元组添加到结果列表res中,并返回。 -
循环遍历从
st(起始索引)到len(nums)的所有整数。每次循环,选择一个数nums[i-1]并从n中减去这个数,表示将这个数纳入当前划分。
-
递归的调用:如果
nums[i-1]小于或等于n,这意味着我们可以将这个数作为当前划分的一部分。我们递归地调用fn,传递新的n值(n - nums[i-1]),索引i(确保不会选择小于当前数字的数字,从而避免重复),以及更新的当前划分cur + [nums[i-1]]。 -
避免重复的划分:通过在每次递归调用中传递
i作为起始索引,我们确保不会出现重复的划分。这是因为我们总是选择当前数字或更大的数字,从而保持了划分中数字的顺序。 -
结束递归:当我们尝试所有可能的数字,并且
n不再减少到0,递归调用将结束。如果n变为负数,我们不做任何事情就返回,因为这意味着当前的划分无法加起来等于N。
整个过程可以视为一棵树,其中每个节点代表一个划分的决策。DFS 遍历这棵树,探索所有可能的路径,即整数 N 的所有可能划分。
res[0:len(res)-1]从结果列表res中省略了最后一个元素。
代码
N = eval(input())
nums = [i for i in range(1, N + 1)]
res = []
def fn(n, st, cur):
if n < 0:
return
if n == 0:
res.append(cur)
return
for i in range(st, len(nums)):
fn(n - nums[i], i, cur + [nums[i]])
fn(N, 0, [])
print(res[0:len(res)-1])
运行结果
N = 4
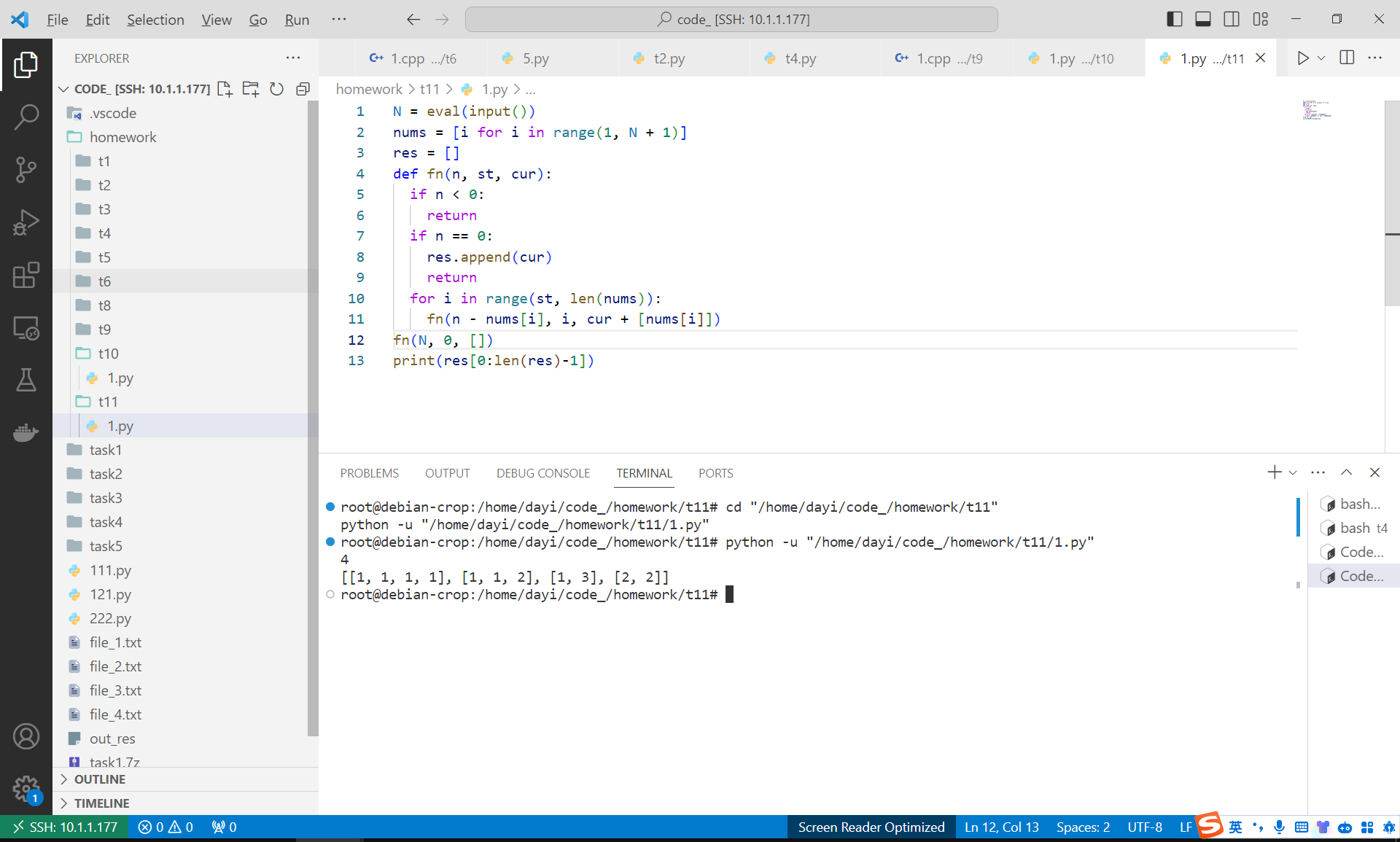
N=15
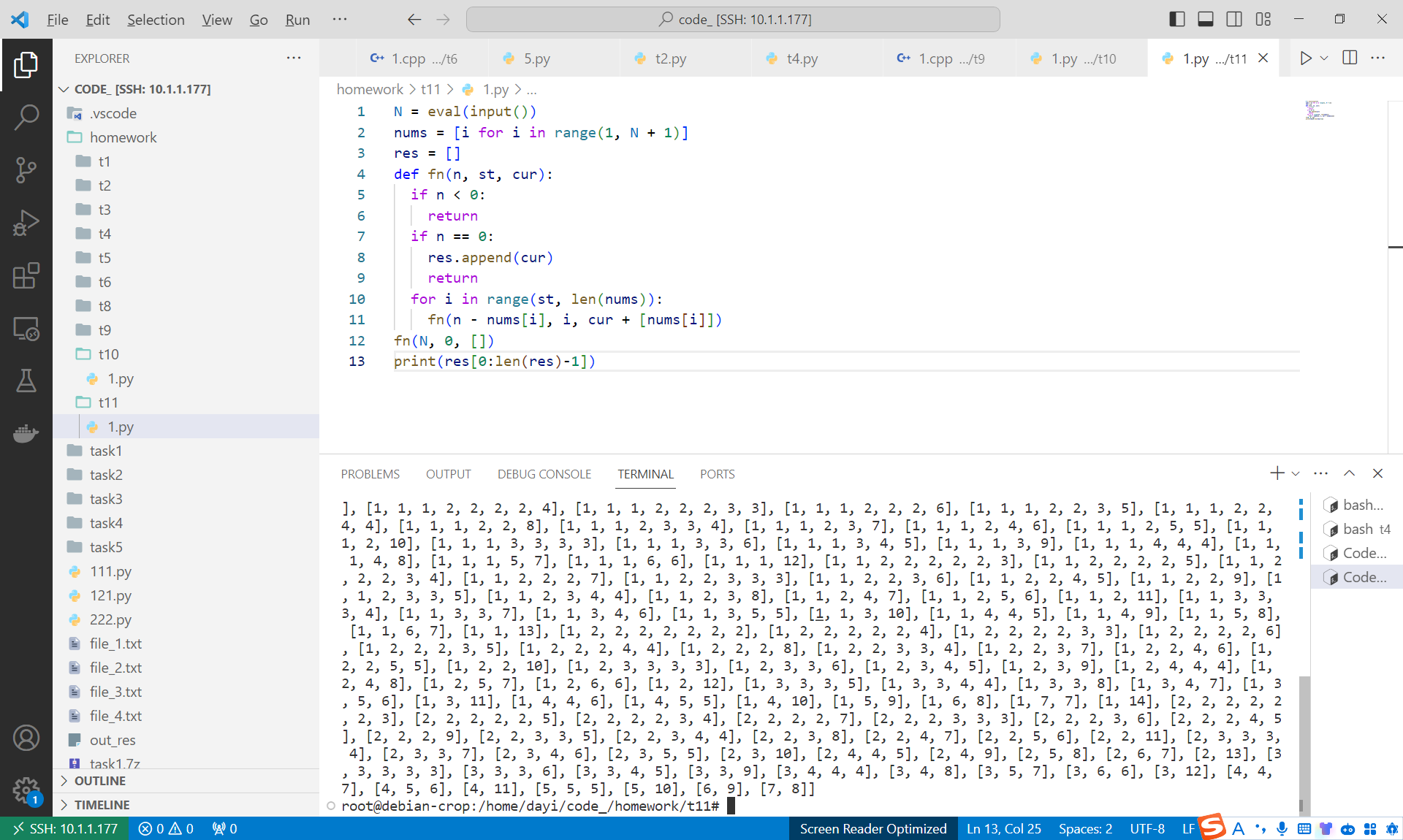
时间复杂度:
-
在这个问题中,递归地遍历所有可能的数字划分。由于每个数字至少可以用一个方式进行划分(即它本身),划分的总数随 \(N\) 增长而指数级增加。
-
更准确地讲,大致可以表示为 \(O(2^N)\) 或者更复杂的指数函数,但这不是一个精确的表达。实际的运行时间还受到具体实现和运行环境的影响。
-
不同的 $ N$ 值会导致非常不同的递归树结构。
P183习题-T2
题目描述
给定一个没有重复数字的数组,输出第k小的元素。例如:
输入:[2,1,3,4,5,0,9],4
输出:3
输入:[6,-1,4,5,2,-10],2
输出:-1
题目解析
排序即可OVO
归并排序代码:
n = int(input())
ls = list(map(int, input().split()))
def merge_sort(l,r):
if l>=r:
return
mid = (l+r)//2
merge_sort(l,mid)
merge_sort(mid+1,r)
i,j = l,mid+1
tmp = []
while i<=mid and j<=r and i<=j:
if ls[i]<ls[j]:
tmp.append(ls[i])
i+=1
else:
tmp.append(ls[j])
j+=1
while j<=r:
tmp.append(ls[j])
j+=1
while i<=mid:
tmp.append(ls[i])
i+=1
for i in range(l, r + 1):
# 注意
ls[i] = tmp[i - l]
merge_sort(0, len(ls) - 1)
print(" ".join(str(i) for i in ls))
快排代码:
n = int(input())
ls = list(map(int, input().split()))
def sort(l, r):
if l >= r:
return
i = l - 1
j = r + 1
import random
val = ls[random.randint(l,r)]
while i < j:
i += 1
while i < r and ls[i] < val:
i += 1
j -= 1
while j > l and ls[j] > val:
j -= 1
if i < j:
ls[i], ls[j] = ls[j], ls[i]
sort(l, j)
sort(j + 1, r)
sort(0, len(ls) - 1)
print(" ".join(str(i) for i in ls))
运行结果
输入1:
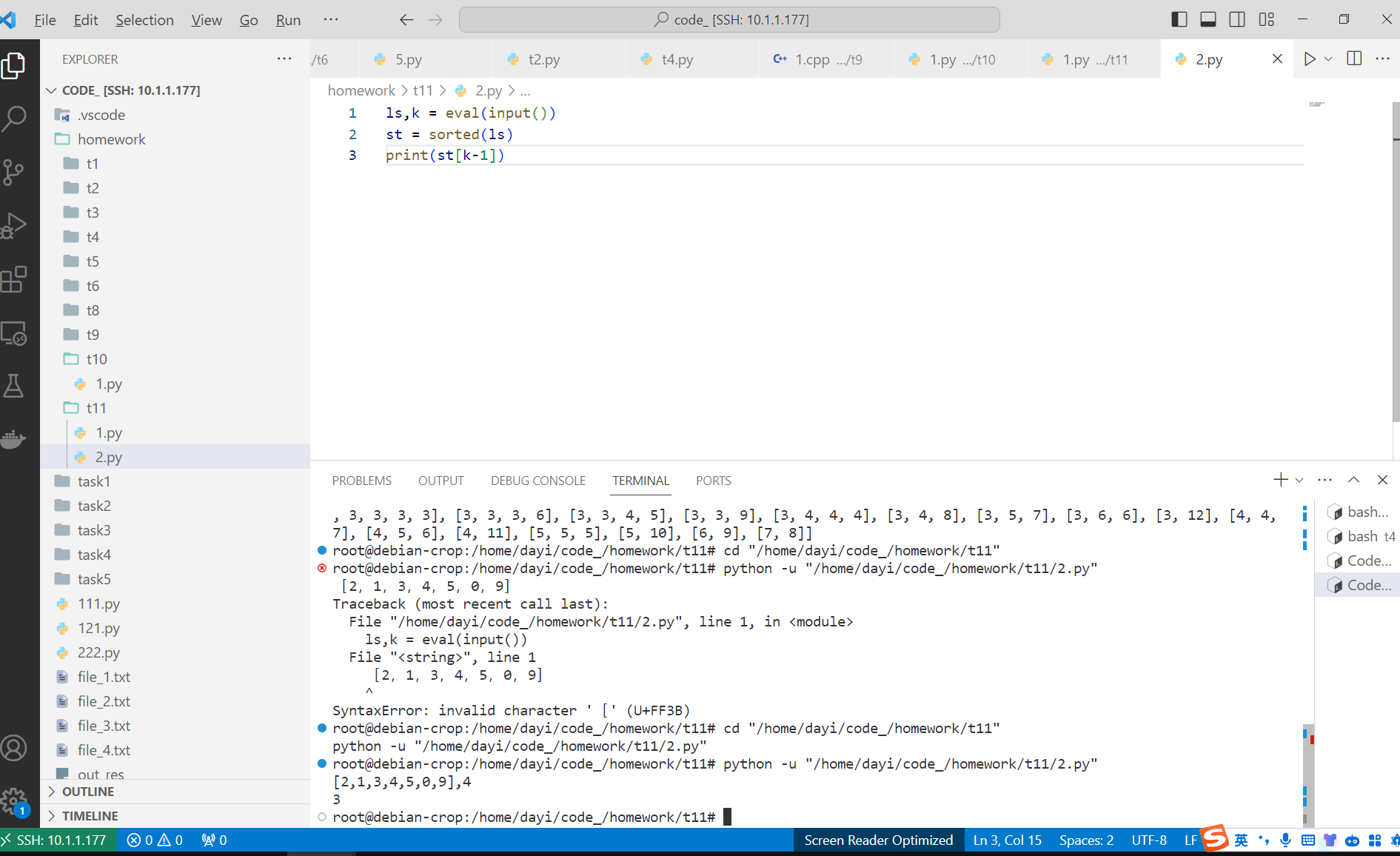
输入2:
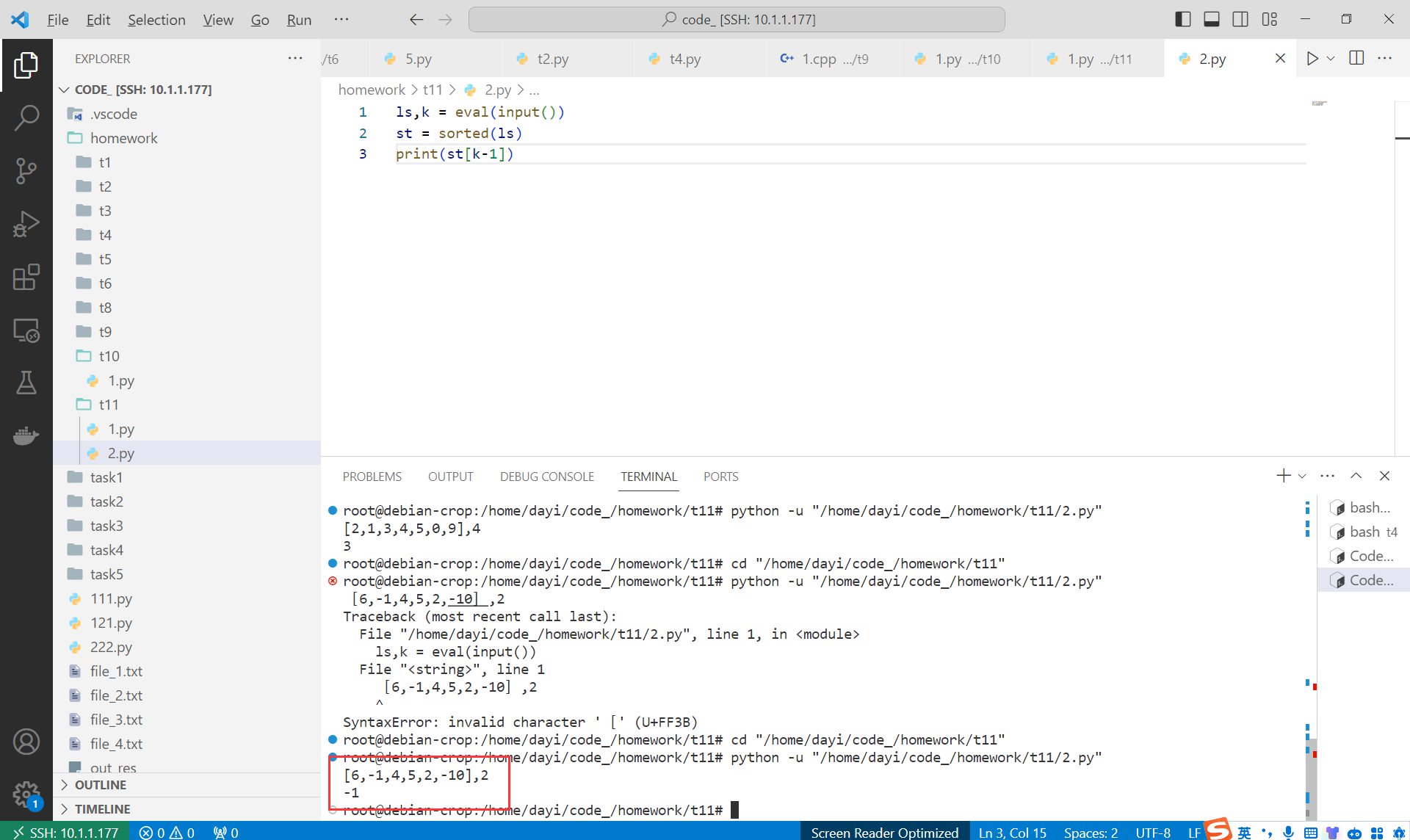
时间复杂度
解决这个问题的两种排序算法,归并排序和快速排序,但是都是\(O(n \log n)\)的复杂度
- 归并排序的实现确保了时间复杂度始终为 \(O(n \log n)\)。
- 快速排序的实现使用随机枢轴选择,平均时间复杂度也为 \(O(n \log n)\)。
在大多数期望下,复杂度为\(O(n \log n)\)
P183习题-T3
3.给定一个数组,输出拥有最大和的连续子数组。例如:
输入:[-1,2,3,-1]
输出:[2,3]
输入:[2,3,-4,5,-1,-10,4,3]
输出:[4,3]
输入:[-1,-2]
输出:[-1]
题目分析
Kadane算法可以在O(N)的时间里去求得答案。
-
初始化:定义两个变量,max_sum 存储遍历到目前为止的最大子数组和,curr_sum 存储包含当前元素的最大子数组和。记录子数组的起始和结束索引,以便最后可以返回子数组本身。
-
遍历整个数组,对于每个元素进行以下操作:
-
更新 curr_sum:如果 current_sum 加上当前元素的和小于当前元素的值,说明从当前元素开始一个新的子数组可能会得到更大的和。
-
更新 curr_sum 为当前元素的值,并记录新子数组的起始位置。
-
如果 curr_sum 加上当前元素的和更大,则累加当前元素的值到 curr_sum。
-
更新 max_sum:在每一步中,我们检查 curr_sum 是否比 max_sum 大。如果是,我们更新 max_sum 为 curr_sum 的值,并更新记录子数组的起始和结束索引。
-
处理特殊情况:如果数组中全部都是负数,则最大子数组和将是数组中的最大单个元素。
也可以枚举区间,双指针,然后\(O(n^3)\)
暴力!
- 枚举区间长度。
- 求最大区间
- 全是负数情况
- 两个指针
-
检查是否所有元素都是负数:
- 检查输入数组
ls是否所有元素都是负数。这是一个特殊情况,因为如果数组中所有元素都是负数,那么最大子数组和就是其中最大的单个元素。 - 直接返回包含这个最大负数的数组。
- 检查输入数组
-
初始化变量:
cmax初始化为负无穷大。它用于存储当前找到的最大子数组和。res初始化为空数组。它将用于存储产生最大和的子数组。
-
遍历所有可能的子数组:
- 使用两个嵌套的
for循环来遍历数组中所有可能的子数组。外层循环 (l) 代表子数组的起始位置,内层循环 (r) 代表子数组的结束位置。 - 对于每一对
(l, r),提取子数组ls[l:r+1]并计算它的和。
- 使用两个嵌套的
-
更新最大和及对应的子数组:
- 如果当前子数组的和大于之前记录的最大和
cmax,则更新cmax为这个新的最大值,并且更新res为当前的子数组。
- 如果当前子数组的和大于之前记录的最大和
-
返回结果:
- 最后,返回和最大的子数组
res。
- 最后,返回和最大的子数组
代码-枚举区间
#O(N*3)
ls = eval(input())
def calc():
n = len(ls)
# 检查是否所有元素都是负数
if all(x < 0 for x in ls):
return [max(ls)]
cmax = -float('inf')
res = []
# 遍历所有可能长度的子数组
for l in range(n):
for r in range(l,n):
tmp_ls = ls[l:r+1]
tmp_sum = sum(tmp_ls)
if tmp_sum > cmax:
cmax = tmp_sum
res = tmp_ls
return res
print(calc())
ls = [-1, 2, 3, -1]
print(calc())
ls = [2, 3, -4, 5, -1, -10, 4, 3]
print(calc())
ls = [-1, -2]
print(calc())
➜ t11 python -u "/home/dayi/code_/homework/t11/t3_2.py"
[1,1,4,5,1,4,-123]
[1, 1, 4, 5, 1, 4]
[2, 3]
[4, 3]
[-1]
➜ t11
代码-Kadane
def solve(nums):
max_sum = nums[0]
curr_sum = nums[0]
start = end = 0
temp_start = 0
for i in range(1, len(nums)):
if nums[i] > curr_sum + nums[i]:
curr_sum = nums[i]
temp_start = i
else:
curr_sum += nums[i]
if curr_sum > max_sum:
max_sum = curr_sum
start = temp_start
end = i
return nums[start:end + 1]
print(solve([-1, 2, 3, -1]))
print(solve([2, 3, -4, 5, -1, -10, 4, 3]))
print(solve([-1, -2]))
时间复杂度
-
\(O(n)\) Kadane
-
\(O(n^{3})\) 暴力
P183习题-T4
有 n 名选手参加一个进行 n-1 天的比赛。每一名选手都需要和其他 n-1 名选手进行一场比赛,且每位选手每天只进行一场比赛。请为比赛安排日程。
输入 n,输出一个二维数组,令第 i 行、第 j 列的值代表第个选手在第 j 天的比赛。
分析
- 选手必须与n-1个选手都进行比赛
- 每个选手一天只赛一次
- 循环赛共进行n-1天
- 选手人数是2的指数幂(如果不足则用虚拟对手补全,当真实对手与虚拟对手竞技=休息)
分治思想。循环赛日程表。先扩展到2的指数幂,然后进行复制和扩展。
-
当
sz(参与选手的数量)为2时,这是递归的基本情况。此时,只有两名选手,他们在第一天进行比赛,所以直接将他们的比赛日程填入数组。 -
对于大于
2的sz,算法首先对sz/2大小的问题进行递归调用。 -
完成对半大小问题的递归后
- 将左上角的数据复制到右下角。前一半的选手在接下来的几天里与后一半的选手进行比赛。
- 扩展左上角和左下角的数据,通过增加
sz/2来调整选手编号,确保所有选手都能参与比赛。
代码和运行结果
#include<bits/stdc++.h>
int N;
struct node{
int whoami;
};
int mp[1024][1024];
inline void debug_print(){
for(int i=1;i<=16;++i){
for(int j=1;j<=16;++j){
std::cout<<mp[i][j]<<" ";
}
std::cout<<"\n";
}std::cout<<"\n";
}
inline void solve(int sz){
if(sz==2){
mp[1][1]=1;
mp[1][2]=2;
mp[2][1]=2;
mp[2][2]=1;
return;
}
solve(sz/2);
//复制当前数据到右下角
for(int i=1;i<=sz/2;++i){
for(int j=1;j<=sz/2;++j){
mp[i+sz/2][j+sz/2]=mp[i][j];
}
}
//扩展左上角和左下角
for(int i=1;i<=sz/2;++i){
for(int j=1;j<=sz/2;++j){
mp[i][j+sz/2]=mp[i][j]+sz/2;
mp[i+sz/2][j]=mp[i][j]+sz/2;
}
}
}
inline void print_res(int n){
using namespace std;
cout<<" ";
for(int i=1;i<=n-1;++i){
cout<<"D"<<i<<" ";
}
cout<<"\n";
for(int i=1;i<=N;++i){
for(int j=1;j<=n;++j){
if(mp[i][j] > N) cout<<"R "; // 只有当值大于 N 时才打印'R'
else cout<<mp[i][j]<<" ";
}
cout<<"\n";
}
}
int main(){
using namespace std;
// N=8;
std::cin>>N;
int n = N;
if((n & (n - 1))!=0){
n = pow(2, ceil(log2(n)));
// printf("xxx:%d",n);
}
solve(n);
// debug_print();
print_res(n);
}
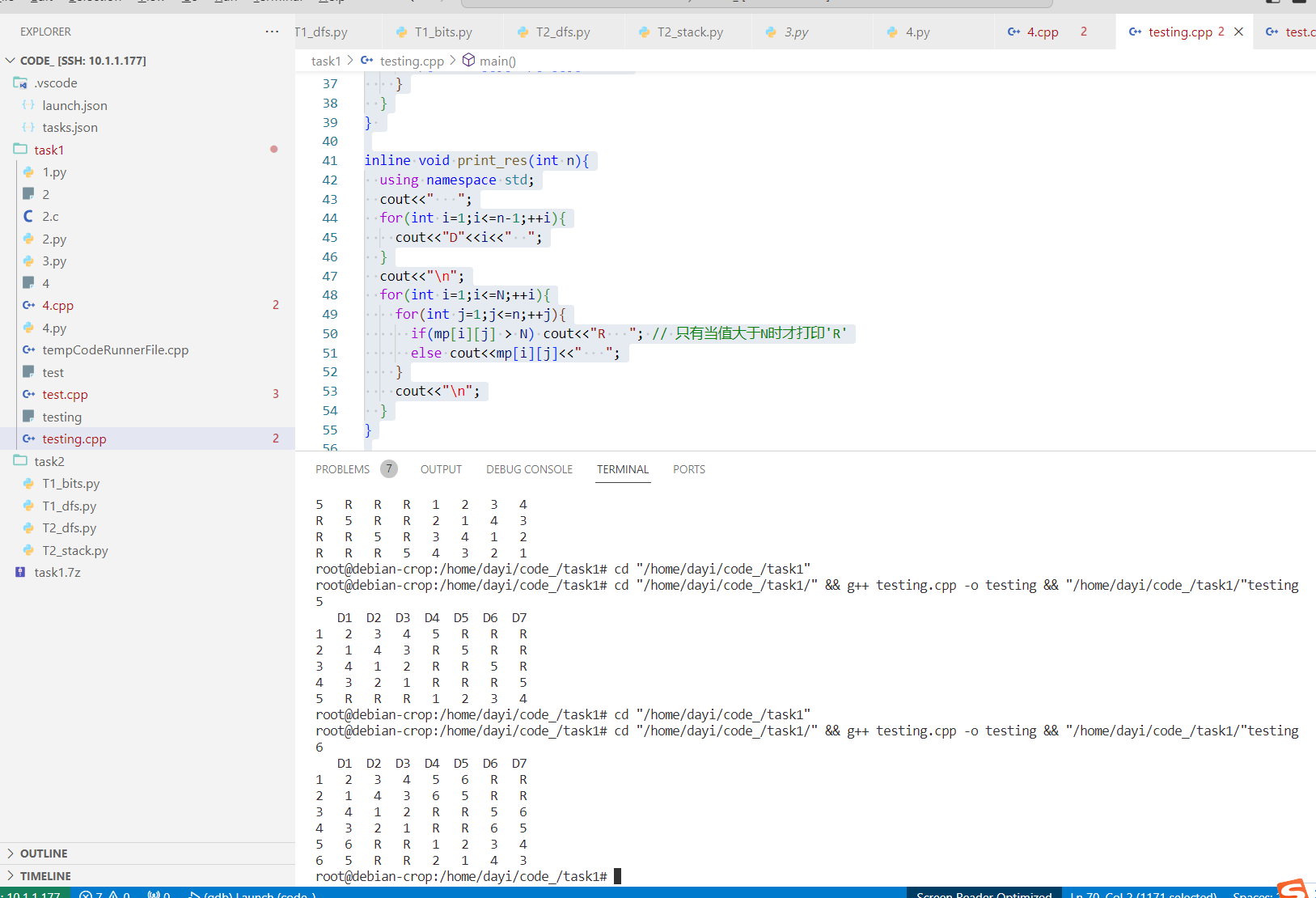
输出结果:
=========2==========
D1
1 2
2 1
=====================
=========3==========
D1 D2 D3
1 2 3 R
2 1 R 3
3 R 1 2
=====================
=========4==========
D1 D2 D3
1 2 3 4
2 1 4 3
3 4 1 2
4 3 2 1
=====================
=========5==========
D1 D2 D3 D4 D5 D6 D7
1 2 3 4 5 R R R
2 1 4 3 R 5 R R
3 4 1 2 R R 5 R
4 3 2 1 R R R 5
5 R R R 1 2 3 4
=====================
=========6==========
D1 D2 D3 D4 D5 D6 D7
1 2 3 4 5 6 R R
2 1 4 3 6 5 R R
3 4 1 2 R R 5 6
4 3 2 1 R R 6 5
5 6 R R 1 2 3 4
6 5 R R 2 1 4 3
=====================
=========7==========
D1 D2 D3 D4 D5 D6 D7
1 2 3 4 5 6 7 R
2 1 4 3 6 5 R 7
3 4 1 2 7 R 5 6
4 3 2 1 R 7 6 5
5 6 7 R 1 2 3 4
6 5 R 7 2 1 4 3
7 R 5 6 3 4 1 2
=====================
=========8==========
D1 D2 D3 D4 D5 D6 D7
1 2 3 4 5 6 7 8
2 1 4 3 6 5 8 7
3 4 1 2 7 8 5 6
4 3 2 1 8 7 6 5
5 6 7 8 1 2 3 4
6 5 8 7 2 1 4 3
7 8 5 6 3 4 1 2
8 7 6 5 4 3 2 1
=====================
=========9==========
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
1 2 3 4 5 6 7 8 9 R R R R R R R
2 1 4 3 6 5 8 7 R 9 R R R R R R
3 4 1 2 7 8 5 6 R R 9 R R R R R
4 3 2 1 8 7 6 5 R R R 9 R R R R
5 6 7 8 1 2 3 4 R R R R 9 R R R
6 5 8 7 2 1 4 3 R R R R R 9 R R
7 8 5 6 3 4 1 2 R R R R R R 9 R
8 7 6 5 4 3 2 1 R R R R R R R 9
9 R R R R R R R 1 2 3 4 5 6 7 8
=====================
=========10==========
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
1 2 3 4 5 6 7 8 9 10 R R R R R R
2 1 4 3 6 5 8 7 10 9 R R R R R R
3 4 1 2 7 8 5 6 R R 9 10 R R R R
4 3 2 1 8 7 6 5 R R 10 9 R R R R
5 6 7 8 1 2 3 4 R R R R 9 10 R R
6 5 8 7 2 1 4 3 R R R R 10 9 R R
7 8 5 6 3 4 1 2 R R R R R R 9 10
8 7 6 5 4 3 2 1 R R R R R R 10 9
9 10 R R R R R R 1 2 3 4 5 6 7 8
10 9 R R R R R R 2 1 4 3 6 5 8 7
=====================
=========11==========
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
1 2 3 4 5 6 7 8 9 10 11 R R R R R
2 1 4 3 6 5 8 7 10 9 R 11 R R R R
3 4 1 2 7 8 5 6 11 R 9 10 R R R R
4 3 2 1 8 7 6 5 R 11 10 9 R R R R
5 6 7 8 1 2 3 4 R R R R 9 10 11 R
6 5 8 7 2 1 4 3 R R R R 10 9 R 11
7 8 5 6 3 4 1 2 R R R R 11 R 9 10
8 7 6 5 4 3 2 1 R R R R R 11 10 9
9 10 11 R R R R R 1 2 3 4 5 6 7 8
10 9 R 11 R R R R 2 1 4 3 6 5 8 7
11 R 9 10 R R R R 3 4 1 2 7 8 5 6
=====================
=========12==========
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
1 2 3 4 5 6 7 8 9 10 11 12 R R R R
2 1 4 3 6 5 8 7 10 9 12 11 R R R R
3 4 1 2 7 8 5 6 11 12 9 10 R R R R
4 3 2 1 8 7 6 5 12 11 10 9 R R R R
5 6 7 8 1 2 3 4 R R R R 9 10 11 12
6 5 8 7 2 1 4 3 R R R R 10 9 12 11
7 8 5 6 3 4 1 2 R R R R 11 12 9 10
8 7 6 5 4 3 2 1 R R R R 12 11 10 9
9 10 11 12 R R R R 1 2 3 4 5 6 7 8
10 9 12 11 R R R R 2 1 4 3 6 5 8 7
11 12 9 10 R R R R 3 4 1 2 7 8 5 6
12 11 10 9 R R R R 4 3 2 1 8 7 6 5
=====================
=========13==========
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
1 2 3 4 5 6 7 8 9 10 11 12 13 R R R
2 1 4 3 6 5 8 7 10 9 12 11 R 13 R R
3 4 1 2 7 8 5 6 11 12 9 10 R R 13 R
4 3 2 1 8 7 6 5 12 11 10 9 R R R 13
5 6 7 8 1 2 3 4 13 R R R 9 10 11 12
6 5 8 7 2 1 4 3 R 13 R R 10 9 12 11
7 8 5 6 3 4 1 2 R R 13 R 11 12 9 10
8 7 6 5 4 3 2 1 R R R 13 12 11 10 9
9 10 11 12 13 R R R 1 2 3 4 5 6 7 8
10 9 12 11 R 13 R R 2 1 4 3 6 5 8 7
11 12 9 10 R R 13 R 3 4 1 2 7 8 5 6
12 11 10 9 R R R 13 4 3 2 1 8 7 6 5
13 R R R 9 10 11 12 5 6 7 8 1 2 3 4
=====================
=========14==========
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
1 2 3 4 5 6 7 8 9 10 11 12 13 14 R R
2 1 4 3 6 5 8 7 10 9 12 11 14 13 R R
3 4 1 2 7 8 5 6 11 12 9 10 R R 13 14
4 3 2 1 8 7 6 5 12 11 10 9 R R 14 13
5 6 7 8 1 2 3 4 13 14 R R 9 10 11 12
6 5 8 7 2 1 4 3 14 13 R R 10 9 12 11
7 8 5 6 3 4 1 2 R R 13 14 11 12 9 10
8 7 6 5 4 3 2 1 R R 14 13 12 11 10 9
9 10 11 12 13 14 R R 1 2 3 4 5 6 7 8
10 9 12 11 14 13 R R 2 1 4 3 6 5 8 7
11 12 9 10 R R 13 14 3 4 1 2 7 8 5 6
12 11 10 9 R R 14 13 4 3 2 1 8 7 6 5
13 14 R R 9 10 11 12 5 6 7 8 1 2 3 4
14 13 R R 10 9 12 11 6 5 8 7 2 1 4 3
=====================
=========15==========
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 R
2 1 4 3 6 5 8 7 10 9 12 11 14 13 R 15
3 4 1 2 7 8 5 6 11 12 9 10 15 R 13 14
4 3 2 1 8 7 6 5 12 11 10 9 R 15 14 13
5 6 7 8 1 2 3 4 13 14 15 R 9 10 11 12
6 5 8 7 2 1 4 3 14 13 R 15 10 9 12 11
7 8 5 6 3 4 1 2 15 R 13 14 11 12 9 10
8 7 6 5 4 3 2 1 R 15 14 13 12 11 10 9
9 10 11 12 13 14 15 R 1 2 3 4 5 6 7 8
10 9 12 11 14 13 R 15 2 1 4 3 6 5 8 7
11 12 9 10 15 R 13 14 3 4 1 2 7 8 5 6
12 11 10 9 R 15 14 13 4 3 2 1 8 7 6 5
13 14 15 R 9 10 11 12 5 6 7 8 1 2 3 4
14 13 R 15 10 9 12 11 6 5 8 7 2 1 4 3
15 R 13 14 11 12 9 10 7 8 5 6 3 4 1 2
=====================
=========16==========
D1 D2 D3 D4 D5 D6 D7 D8 D9 D10 D11 D12 D13 D14 D15
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2 1 4 3 6 5 8 7 10 9 12 11 14 13 16 15
3 4 1 2 7 8 5 6 11 12 9 10 15 16 13 14
4 3 2 1 8 7 6 5 12 11 10 9 16 15 14 13
5 6 7 8 1 2 3 4 13 14 15 16 9 10 11 12
6 5 8 7 2 1 4 3 14 13 16 15 10 9 12 11
7 8 5 6 3 4 1 2 15 16 13 14 11 12 9 10
8 7 6 5 4 3 2 1 16 15 14 13 12 11 10 9
9 10 11 12 13 14 15 16 1 2 3 4 5 6 7 8
10 9 12 11 14 13 16 15 2 1 4 3 6 5 8 7
11 12 9 10 15 16 13 14 3 4 1 2 7 8 5 6
12 11 10 9 16 15 14 13 4 3 2 1 8 7 6 5
13 14 15 16 9 10 11 12 5 6 7 8 1 2 3 4
14 13 16 15 10 9 12 11 6 5 8 7 2 1 4 3
15 16 13 14 11 12 9 10 7 8 5 6 3 4 1 2
16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
=====================
直接照着抄为python
import math
N = None
mp = [[0 for _ in range(1024)] for _ in range(1024)]
def debug_print():
for i in range(1, 17):
for j in range(1, 17):
print(f"{mp[i][j]:2d}", end=" ")
print()
print()
def solve(sz):
if sz == 2:
mp[1][1] = 1
mp[1][2] = 2
mp[2][1] = 2
mp[2][2] = 1
return
solve(sz // 2)
# 复制当前数据到右下角
for i in range(1, sz // 2 + 1):
for j in range(1, sz // 2 + 1):
mp[i + sz // 2][j + sz // 2] = mp[i][j]
# 扩展左上角和左下角
for i in range(1, sz // 2 + 1):
for j in range(1, sz // 2 + 1):
mp[i][j + sz // 2] = mp[i][j] + sz // 2
mp[i + sz // 2][j] = mp[i][j] + sz // 2
def print_res(n):
print(" ", end="")
for i in range(1, n):
print(f"D{i} ", end="")
print()
for i in range(1, N + 1):
for j in range(1, n + 1):
if mp[i][j] > N:
print("R ", end="")
else:
print(f"{mp[i][j]:<4}", end="")
print()
def init():
global N
n = N
if (n & (n - 1)) != 0:
n = 2 ** math.ceil(math.log2(n))
solve(n)
# debug_print()
print_res(n)
if __name__ == "__main__":
for i in range(2, 17):
N = i
print(f"========={i}==========")
init()
print("=====================")
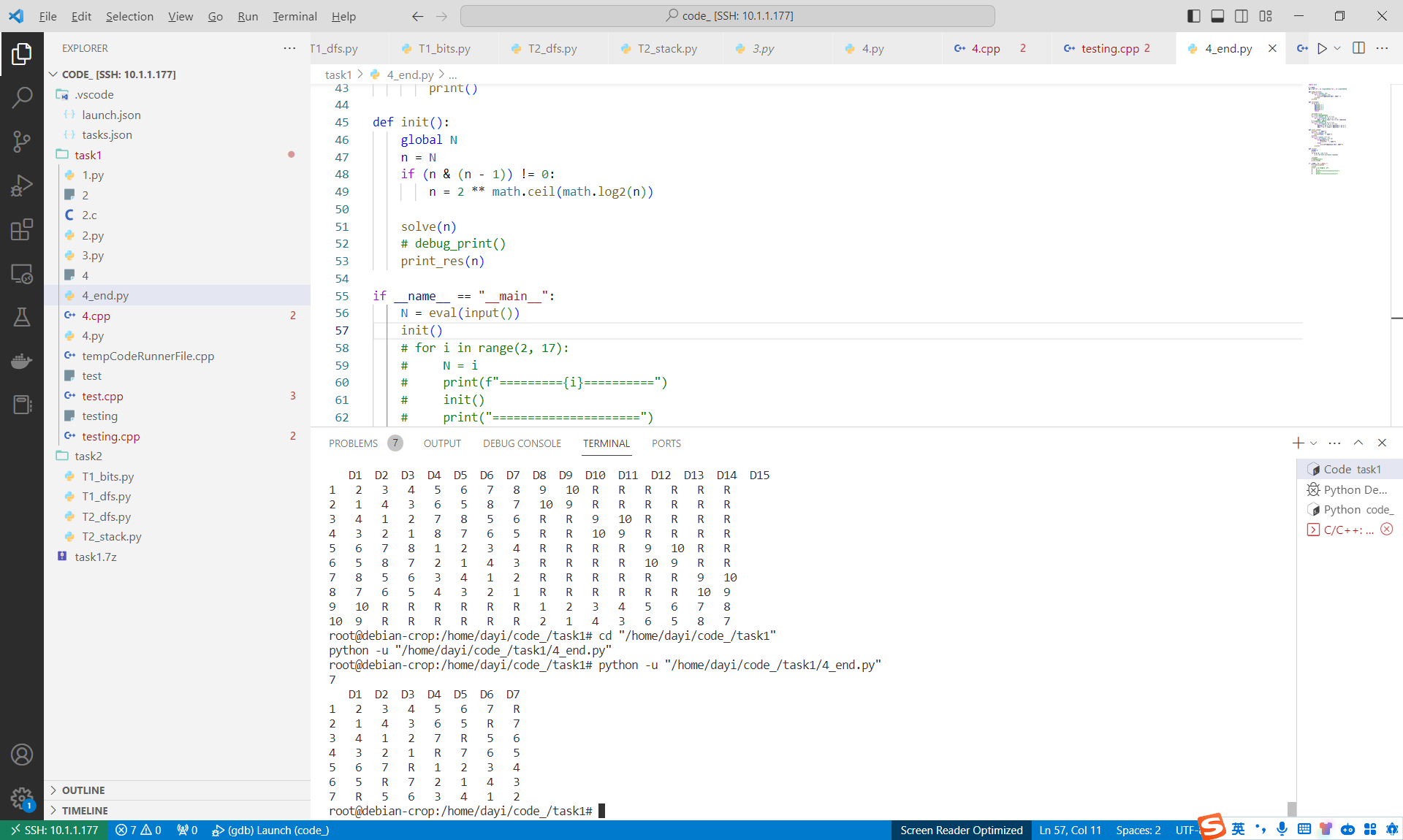
时间复杂度分析
算法的时间复杂度可以通过观察递归调用的数量和每次调用所做的工作来分析。
-
每次递归调用处理规模为原始问题一半的子问题。递归深度是 \(O(\log n)\),其中 \(n\) 是参与选手的数量。
-
在每次递归调用中,算法复制并修改一个 \(frac{sz}{2} \times \frac{sz}{2}\) 的矩阵。对于大小为 \(n\) 的问题,这个工作量大约是 \(O(n^2)\)。
-
递归深度是 \(O(\log n)\),且每层的工作量大约是 \(O(n^2)\),总的时间复杂度是 \(O(n^2 \log n)\)。
实验总结
-
数字划分问题:
- 这个问题涉及到了递归和回溯算法的应用,它教会了我如何系统地探索问题的所有可能解决方案,并从中找到有效解。理解和实现递归函数是这个实验的核心,我学到了如何递归地分解问题,以及如何通过限制条件避免重复和无效的解。我也认识到了递归算法在处理大规模问题时可能面临的效率问题。
-
查找数组中第k小的元素:
- 通过实现归并排序和快速排序,我加深了对这两种经典排序算法的理解。我学习到了如何有效地比较和移动元素以排序数组,以及如何通过随机化改进快速排序的平均性能。认识到了不同算法在不同情况下的性能差异,以及如何根据具体问题选择合适的算法。
-
日程安排问题:
- 我了解到了算法在现实世界问题中的应用。我学到了如何使用递归分而治之的策略来解决复杂的日程安排问题。学会了如何在算法设计中平衡不同的需求和限制条件。
-
最大和的连续子数
-
Kadane 算法的理解与应用:
- Kadane 算法在 O(N) 时间内找到具有最大和的连续子数组。在一次遍历中同时更新当前子数组的最大和和整体最大子数组和。提高了效率,而且优化了空间复杂度。
-
暴力解法的局限性:
- 暴力解法,枚举所有可能子数组的方法虽然直观,但在大规模数据下效率极低。这种方法的时间复杂度为 O(N^3),对于大数据集来说,这是不可接受的。
- 提升
- 实现上述算法的过程中,我提高了我的编程能力和问题解决技巧。将理论算法转化为有效的程序代码,调试和优化这些代码。