01背包问题
01背包是一种动态规划问题。动态规划的核心就是状态转移方程
有一个容量为V的背包,还有n个物体。现在忽略物体实际几何形状,我们认为只要背包的剩余容量大于等于物体体积,那就可以装进背包里。每个物体都有两个属性,即体积w和价值v。 问:如何向背包装物体才能使背包中物体的总价值最大?
二维数组解法
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[j])
i:选用前i种物品
j:背包容量为j
dp[i][j] 表示从下标为[0,i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
for (int j = 0 ; j < weight[0]; j++) { // 如果把dp数组预先初始化为0了,这一步就可以省略。
dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagWeight; j++) {
dp[0][j] = value[0];
}
有两个遍历维度:1. 物品和背包容量。 2. 所以要确定遍历顺序。
两者都可以,先遍历物品好理解。
先遍历物品,然后遍历背包重量:
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 如果不能放下物品i
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
先遍历背包,再遍历物品:
// weight数组的大小就是物品个数
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 1; i < weight.size(); i++) { // 遍历物品
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
为什么两种顺序都可以?要理解递归的本质和递推的方向。那么先遍历物品,再遍历背包的过程和先遍历背包,再遍历物品,dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导。
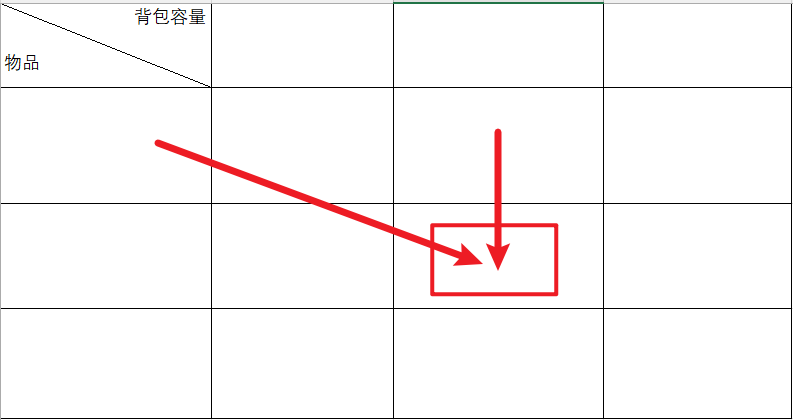
一维dp数组解决01背包问题
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
一维dp数组遍历顺序
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
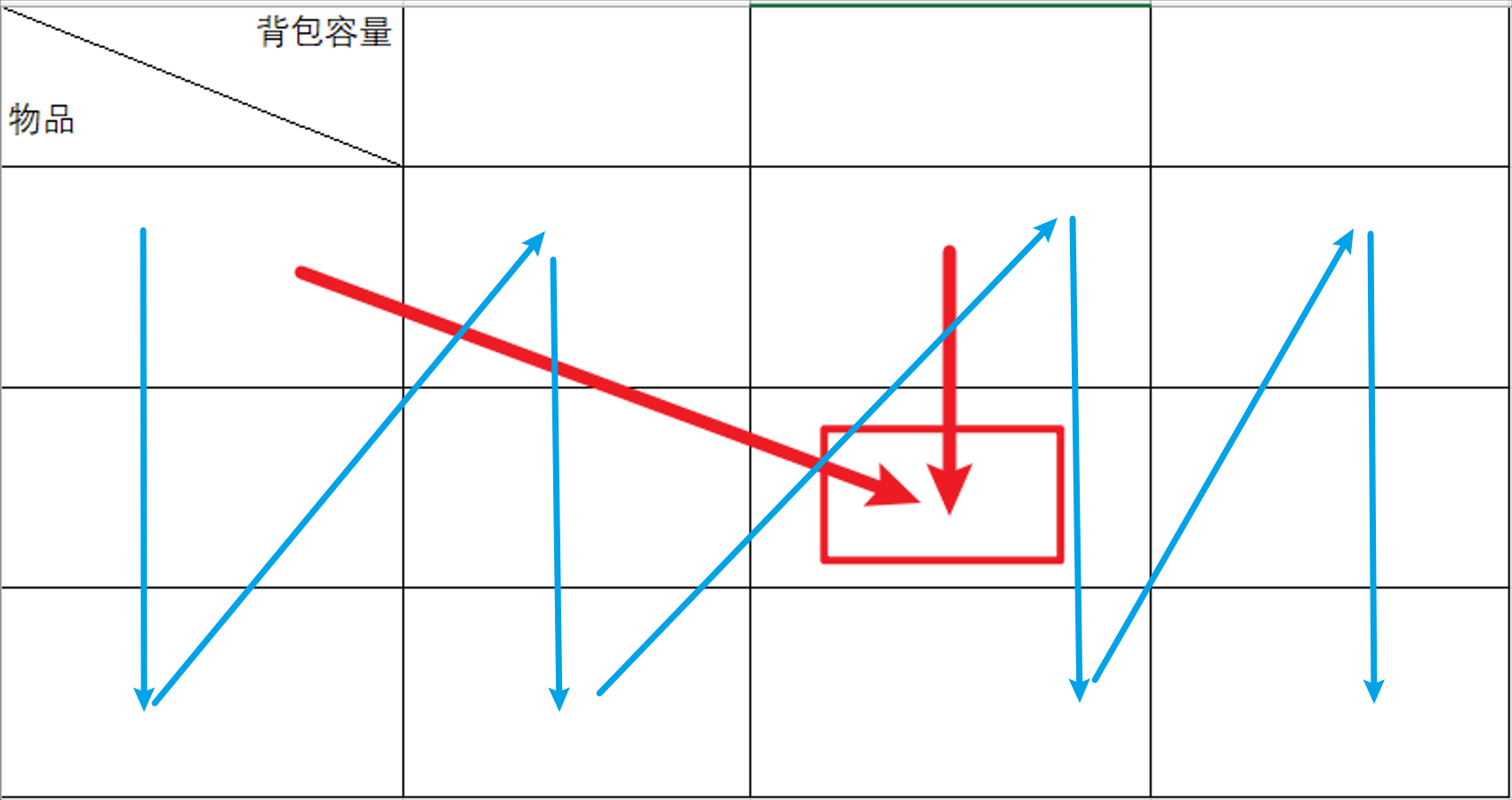
-
在01背包中二维dp数组的两个for遍历的先后循序是可以颠倒,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
-
和二维dp的写法中,遍历背包的顺序是不一样的!一维dp遍历的时候,背包容量是从大到小:倒序遍历是为了保证物品i只被放入一次!
为什么一维dp数组必须倒序遍历:
如图,红线为数据更新来源,蓝线数据更新顺序:当前状态源于左上角和同背包容量方向
- 如果先遍历物品再遍历背包且正序遍历,就会使一些同背包容量方向的数据被覆盖掉。
- 如果先遍历背包再遍历物品,
完全背包问题
完全背包依然是一个动态规划问题
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
01背包和完全背包唯一不同就是体现在遍历顺序上,所以针对遍历顺序进行分析。
// 先遍历物品,再遍历背包
int[] dp = new int[bagWeight + 1];
for (int i = 0; i < weight.length; i++){
for (int j = 1; j <= bagWeight; j++){
if (j - weight[i] >= 0){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
}
为什么遍历物品在外层循环,遍历背包容量在内层循环?
在01背包中二维dp数组的两个for遍历的先后循序是可以颠倒,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序无所谓:因为物品可以重复装。也就是说dp[j]是根据下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以。完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值。
为什么是正序遍历而不是倒序遍历了?
因为在完全背包中,由于物品可以重复装填,那么就需要相同物品在不同背包容量时重复利用前面的数据。
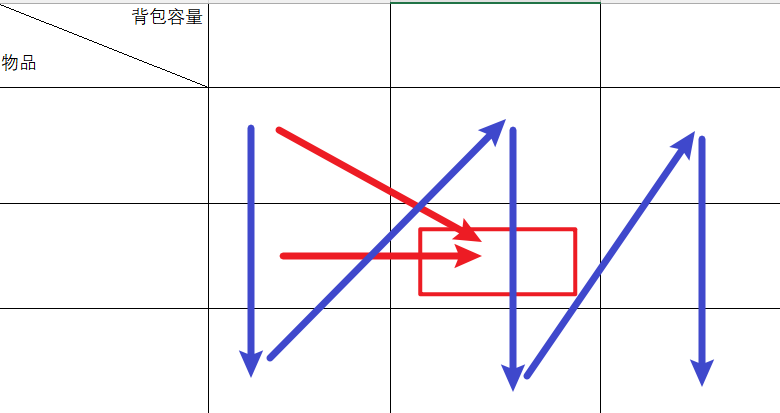
先遍历背包再遍历物品:
// 先遍历背包,再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 0; i < weight.size(); i++) { // 遍历物品
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
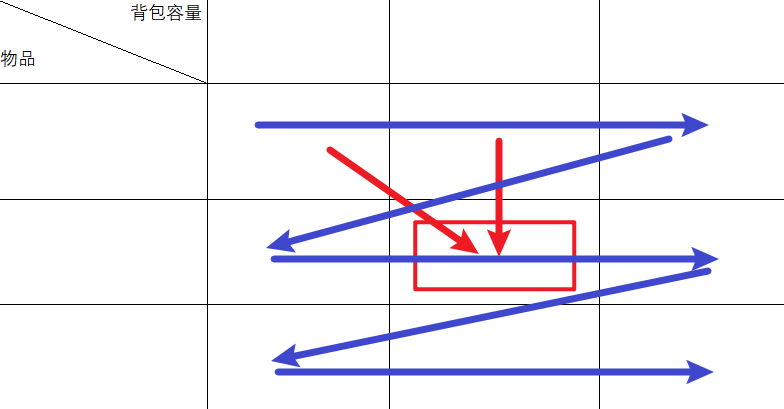
先遍历物品,再遍历背包:
// 先遍历物品,再遍历背包
int[] dp = new int[bagWeight + 1];
for (int i = 0; i < weight.length; i++){
for (int j = 1; j <= bagWeight; j++){
if (j - weight[i] >= 0){
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
}
连续背包问题
连续背包问题是指有一个容量为V的背包和n个物品,每个物品有一个体积v [i]和一个价值w [i],现在要将这些物品放入背包中,使得背包中物品的总价值最大。 与0/1背包问题不同的是,每个物品可以被放入多次,即是连续的。
解题思路:单位价值优先使用贪心算法
① 按价值密度(w/v)进行非递增排序
② 按照排序先后,往里装。单个物品装完时换下一个,直到背包填满为止
标签:遍历,weight,int,问题,算法,背包,物品,dp From: https://www.cnblogs.com/moyiv/p/17854416.html