首页 > 编程语言 >【11.0】Python基础之可变和不可变数据类型

【11.0】Python基础之可变和不可变数据类型

时间：2023-11-18 15:24:51浏览次数：48  
标签：Python 数据类型 self 元素 11.0 int print 节点 def

【一】堆

【0】引入

堆

【1】堆的介绍

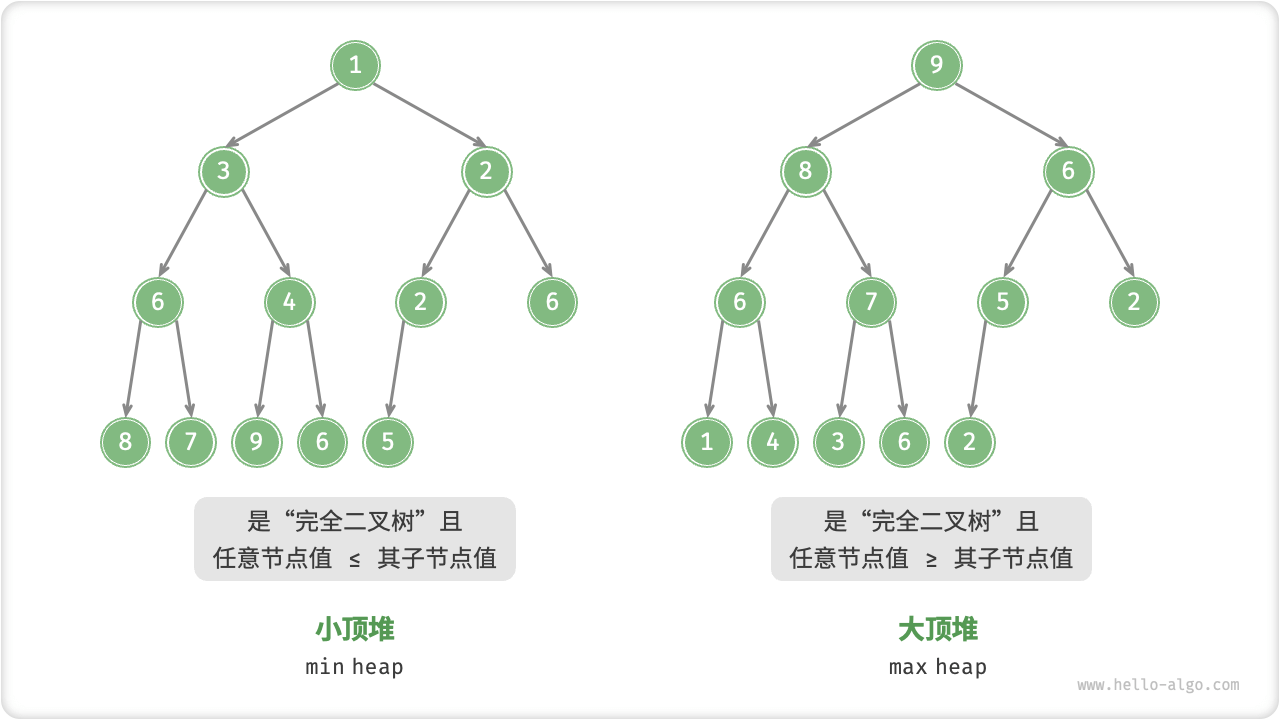
  • 「堆 heap」是一种满足特定条件的完全二叉树，主要可分为图 8-1 所示的两种类型。

    • 「大顶堆 max heap」：任意节点的值 ≥ 其子节点的值。

    • 「小顶堆 min heap」：任意节点的值 ≤ 其子节点的值。

小顶堆与大顶堆

  • 堆作为完全二叉树的一个特例，具有以下特性。

    • 最底层节点靠左填充，其他层的节点都被填满。

    • 我们将二叉树的根节点称为“堆顶”，将底层最靠右的节点称为“堆底”。

    • 对于大顶堆（小顶堆），堆顶元素（即根节点）的值分别是最大（最小）的。

  • 类似于排序算法中的“从小到大排列”和“从大到小排列”，我们可以通过修改 Comparator 来实现“小顶堆”与“大顶堆”之间的转换。

【2】堆的实现

  • 下文实现的是大顶堆。若要将其转换为小顶堆，只需将所有大小逻辑判断取逆

【3】基于数组的实现

（1）堆的存储与表示

  • 我们在二叉树章节中学习到，完全二叉树非常适合用数组来表示。
    • 由于堆正是一种完全二叉树，我们将采用数组来存储堆。
  • 当使用数组表示二叉树时，元素代表节点值，索引代表节点在二叉树中的位置。
    • 节点指针通过索引映射公式来实现。

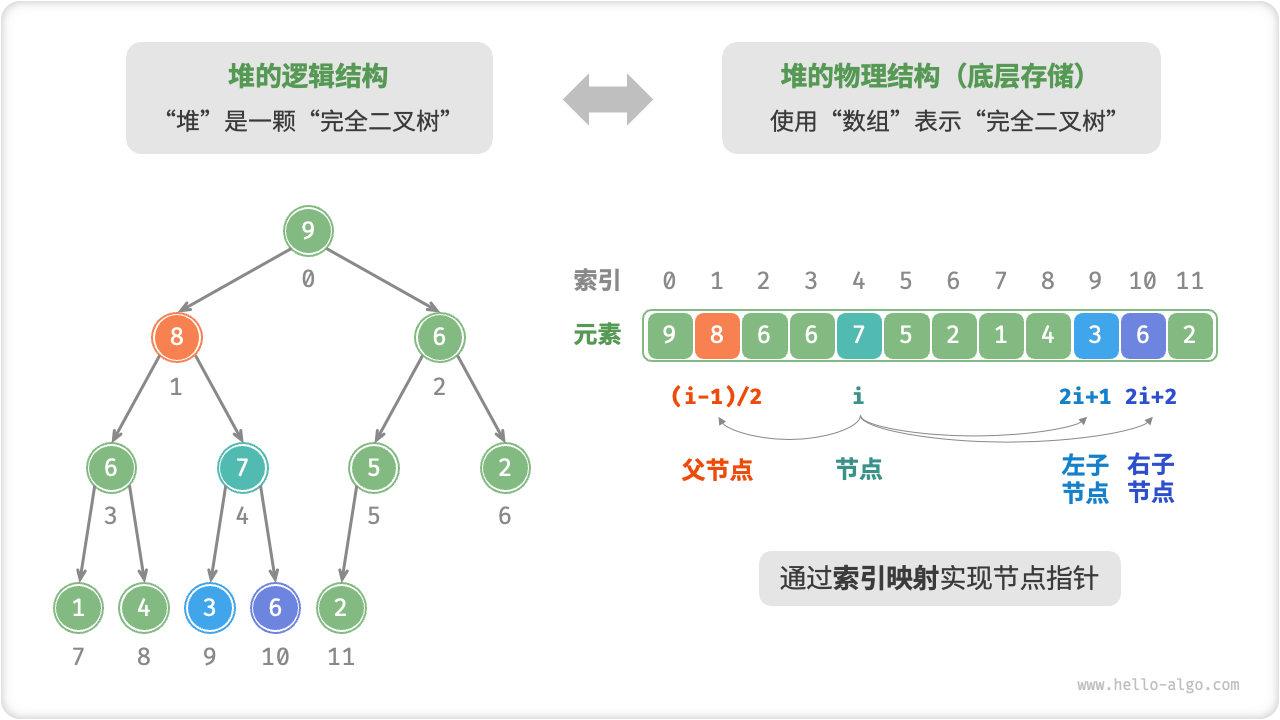
堆的表示与存储

  • 我们可以将索引映射公式封装成函数，方便后续使用。
def left(self, i: int) -> int:
    """获取左子节点索引"""
    return 2 * i + 1

def right(self, i: int) -> int:
    """获取右子节点索引"""
    return 2 * i + 2

def parent(self, i: int) -> int:
    """获取父节点索引"""
    return (i - 1) // 2  # 向下整除

（2）访问堆顶元素

  • 堆顶元素即为二叉树的根节点，也就是列表的首个元素。
def peek(self) -> int:
    """访问堆顶元素"""
    return self.max_heap[0]

（3）元素入堆

  • 给定元素 val ，我们首先将其添加到堆底。添加之后，由于 val 可能大于堆中其他元素，堆的成立条件可能已被破坏。
    • 因此，需要修复从插入节点到根节点的路径上的各个节点，这个操作被称为「堆化 heapify」。
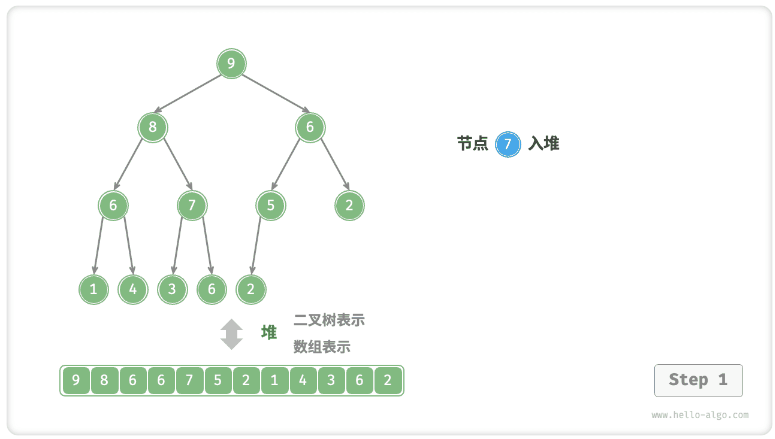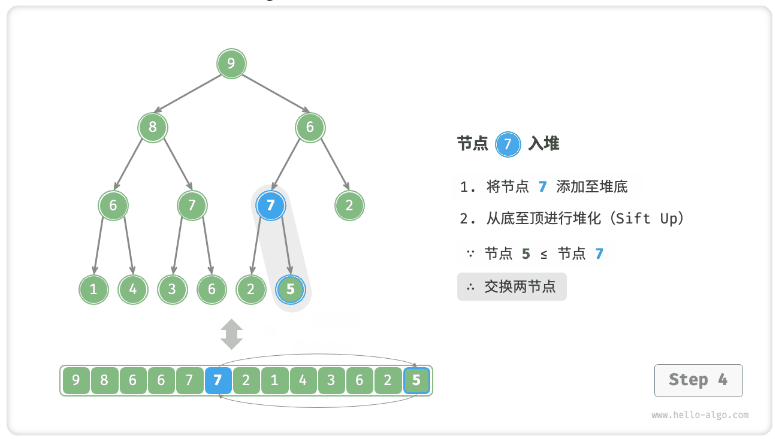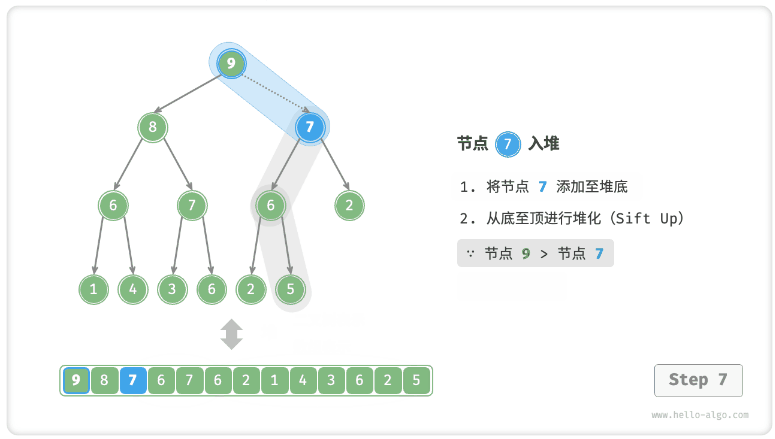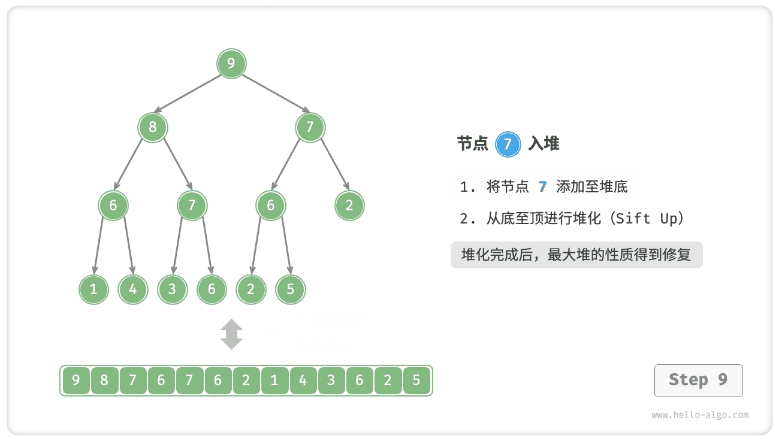
  • 考虑从入堆节点开始，从底至顶执行堆化。
    • 如图 8-3 所示，我们比较插入节点与其父节点的值，如果插入节点更大，则将它们交换。
    • 然后继续执行此操作，从底至顶修复堆中的各个节点，直至越过根节点或遇到无须交换的节点时结束。

动画

def push(self, val: int):
    """元素入堆"""
    # 添加节点
    self.max_heap.append(val)
    # 从底至顶堆化
    self.sift_up(self.size() - 1)

def sift_up(self, i: int):
    """从节点 i 开始，从底至顶堆化"""
    while True:
        # 获取节点 i 的父节点
        p = self.parent(i)
        # 当“越过根节点”或“节点无须修复”时，结束堆化
        if p < 0 or self.max_heap[i] <= self.max_heap[p]:
            break
        # 交换两节点
        self.swap(i, p)
        # 循环向上堆化
        i = p

（4）堆顶元素出堆

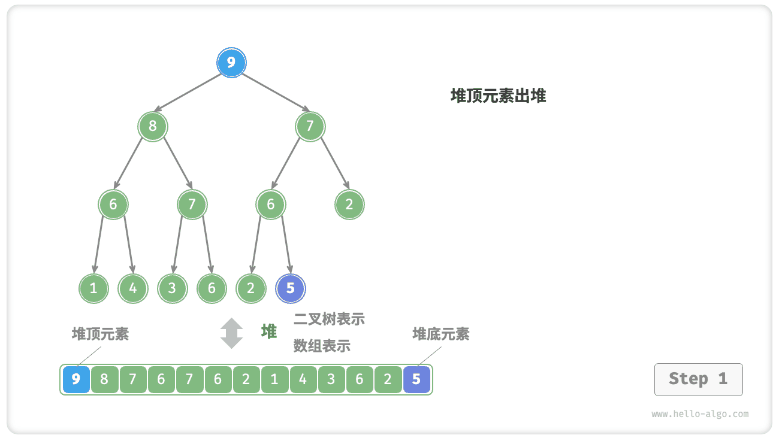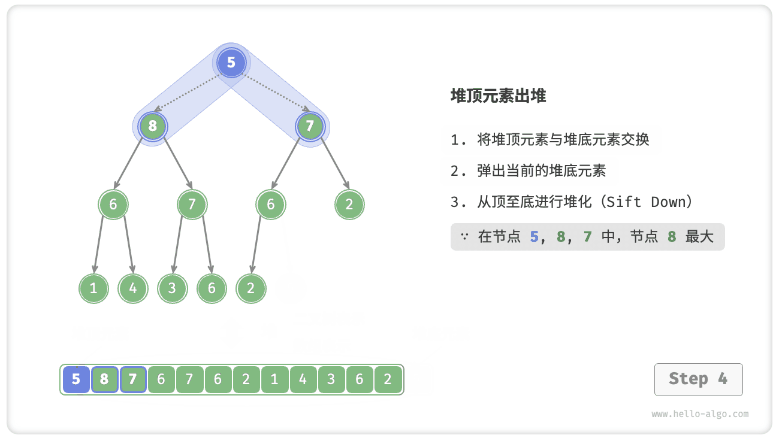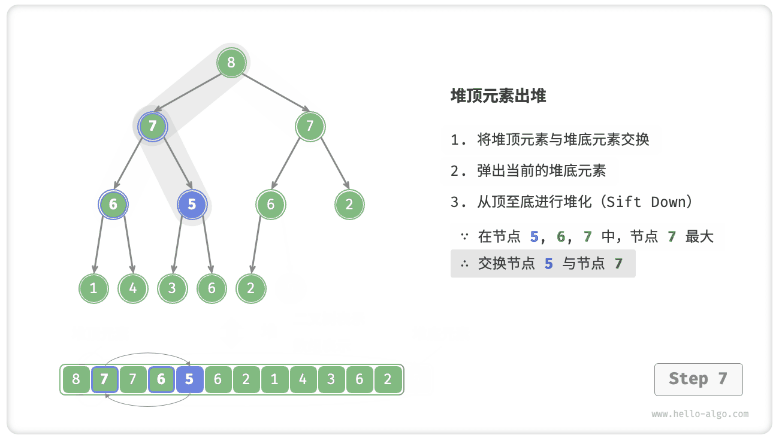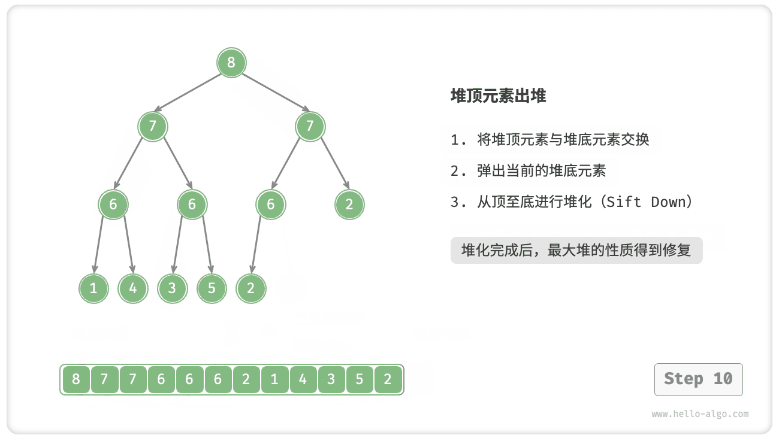
  • 堆顶元素是二叉树的根节点，即列表首元素。如果我们直接从列表中删除首元素，那么二叉树中所有节点的索引都会发生变化，这将使得后续使用堆化修复变得困难。为了尽量减少元素索引的变动，我们采用以下操作步骤。
    • 交换堆顶元素与堆底元素（即交换根节点与最右叶节点）。
    • 交换完成后，将堆底从列表中删除（注意，由于已经交换，实际上删除的是原来的堆顶元素）。
    • 从根节点开始，从顶至底执行堆化。
  • 如图 8-4 所示，“从顶至底堆化”的操作方向与“从底至顶堆化”相反，我们将根节点的值与其两个子节点的值进行比较，将最大的子节点与根节点交换。然后循环执行此操作，直到越过叶节点或遇到无须交换的节点时结束。

动画

def pop(self) -> int:
    """元素出堆"""
    # 判空处理
    if self.is_empty():
        raise IndexError("堆为空")
    # 交换根节点与最右叶节点（即交换首元素与尾元素）
    self.swap(0, self.size() - 1)
    # 删除节点
    val = self.max_heap.pop()
    # 从顶至底堆化
    self.sift_down(0)
    # 返回堆顶元素
    return val

def sift_down(self, i: int):
    """从节点 i 开始，从顶至底堆化"""
    while True:
        # 判断节点 i, l, r 中值最大的节点，记为 ma
        l, r, ma = self.left(i), self.right(i), i
        if l < self.size() and self.max_heap[l] > self.max_heap[ma]:
            ma = l
        if r < self.size() and self.max_heap[r] > self.max_heap[ma]:
            ma = r
        # 若节点 i 最大或索引 l, r 越界，则无须继续堆化，跳出
        if ma == i:
            break
        # 交换两节点
        self.swap(i, ma)
        # 循环向下堆化
        i = ma

【4】堆常见应用

  • 优先队列：堆通常作为实现优先队列的首选数据结构，其入队和出队操作的时间复杂度均为O(log n),而建队操作为 O(n) ，这些操作都非常高效。
  • 堆排序：给定一组数据，我们可以用它们建立一个堆，然后不断地执行元素出堆操作，从而得到有序数据。然而，我们通常会使用一种更优雅的方式实现堆排序，详见后续的堆排序章节。
  • 获取最大的 k 个元素：这是一个经典的算法问题，同时也是一种典型应用，例如选择热度前 10 的新闻作为微博热搜，选取销量前 10 的商品等。

【二】栈

【0】引入

栈与队列

【1】栈的介绍

  • 「栈 stack」是一种遵循先入后出的逻辑的线性数据结构。
  • 我们可以将栈类比为桌面上的一摞盘子，如果需要拿出底部的盘子，则需要先将上面的盘子依次取出。
    • 我们将盘子替换为各种类型的元素（如整数、字符、对象等），就得到了栈数据结构。
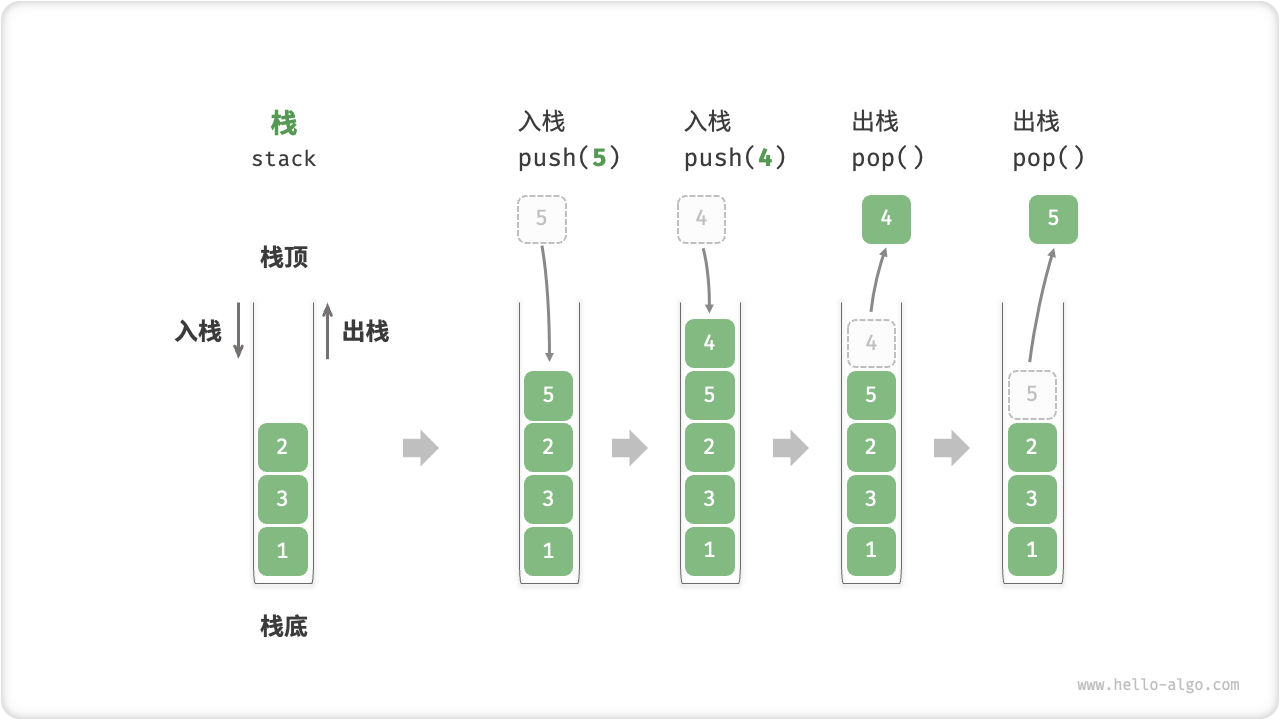
  • 如图 5-1 所示，我们把堆叠元素的顶部称为“栈顶”，底部称为“栈底”。
    • 将把元素添加到栈顶的操作叫做“入栈”，删除栈顶元素的操作叫做“出栈”。

栈的先入后出规则

【2】栈的实现

  • 栈遵循先入后出的原则，因此我们只能在栈顶添加或删除元素。
  • 然而，数组和链表都可以在任意位置添加和删除元素，因此栈可以被视为一种受限制的数组或链表。
  • 换句话说，我们可以“屏蔽”数组或链表的部分无关操作，使其对外表现的逻辑符合栈的特性。

【3】基于链表的实现

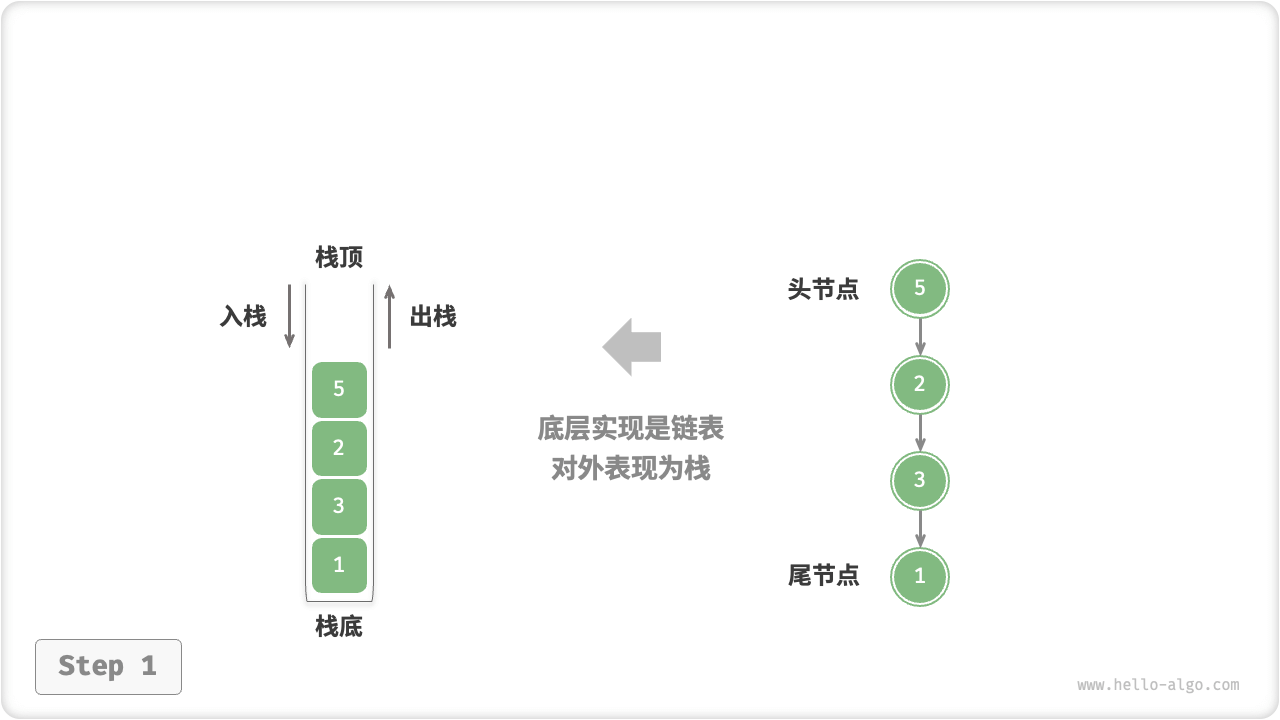
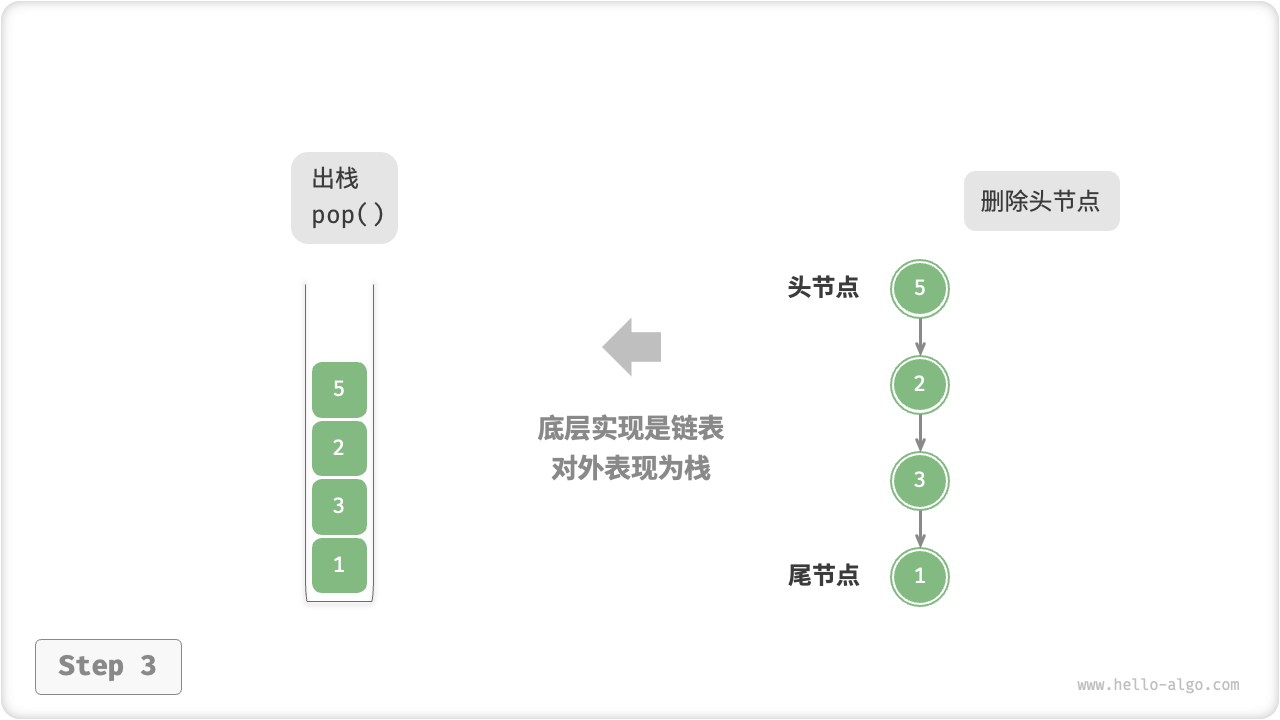
  • 使用链表来实现栈时，我们可以将链表的头节点视为栈顶，尾节点视为栈底。
  • 如图 5-2 所示，对于入栈操作，我们只需将元素插入链表头部，这种节点插入方法被称为“头插法”。
  • 而对于出栈操作，只需将头节点从链表中删除即可。

（1）基于链表图解

  • LinkedListStack

基于链表实现栈的入栈出栈操作

  • push()

linkedlist_stack_push

  • pop()

linkedlist_stack_pop

（2）基于链表代码

class LinkedListStack:
    """基于链表实现的栈"""

    def __init__(self):
        """构造方法"""
        self._peek: ListNode | None = None
        self._size: int = 0

    def size(self) -> int:
        """获取栈的长度"""
        return self._size

    def is_empty(self) -> bool:
        """判断栈是否为空"""
        return not self._peek

    def push(self, val: int):
        """入栈"""
        node = ListNode(val)
        node.next = self._peek
        self._peek = node
        self._size += 1

    def pop(self) -> int:
        """出栈"""
        num = self.peek()
        self._peek = self._peek.next
        self._size -= 1
        return num

    def peek(self) -> int:
        """访问栈顶元素"""
        if self.is_empty():
            raise IndexError("栈为空")
        return self._peek.val

    def to_list(self) -> list[int]:
        """转化为列表用于打印"""
        arr = []
        node = self._peek
        while node:
            arr.append(node.val)
            node = node.next
        arr.reverse()
        return arr

【4】基于数组的实现

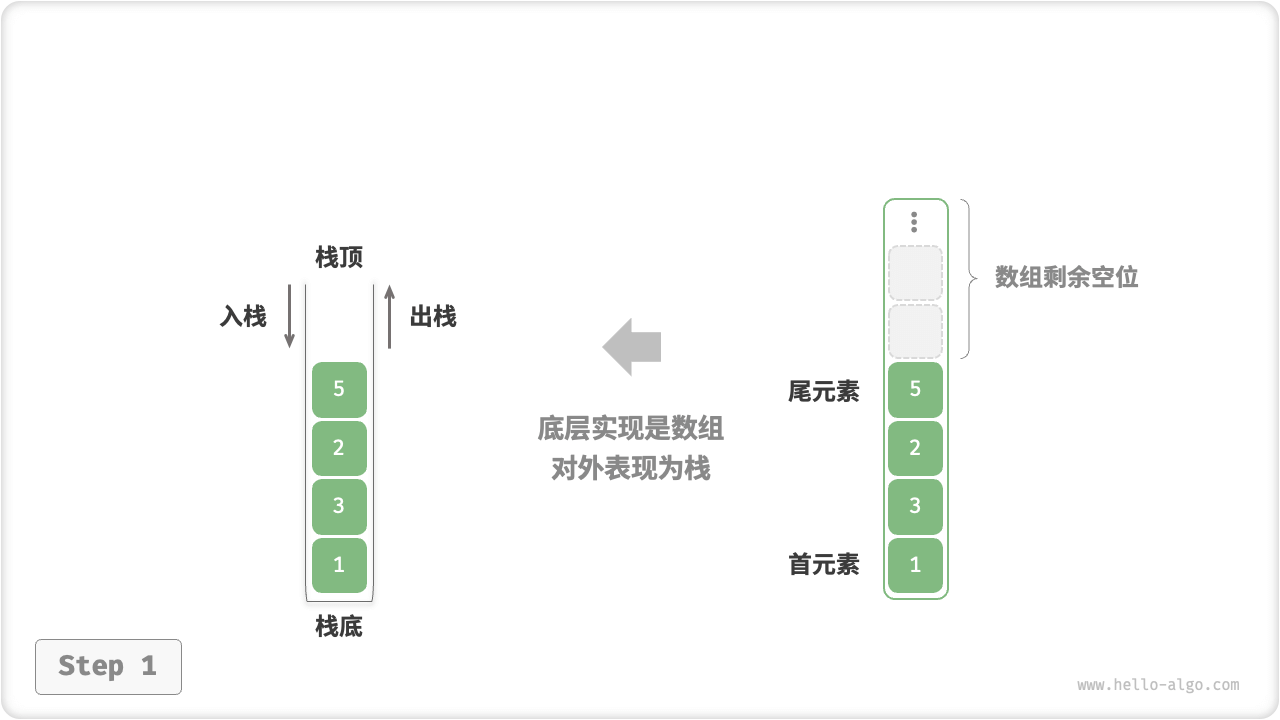
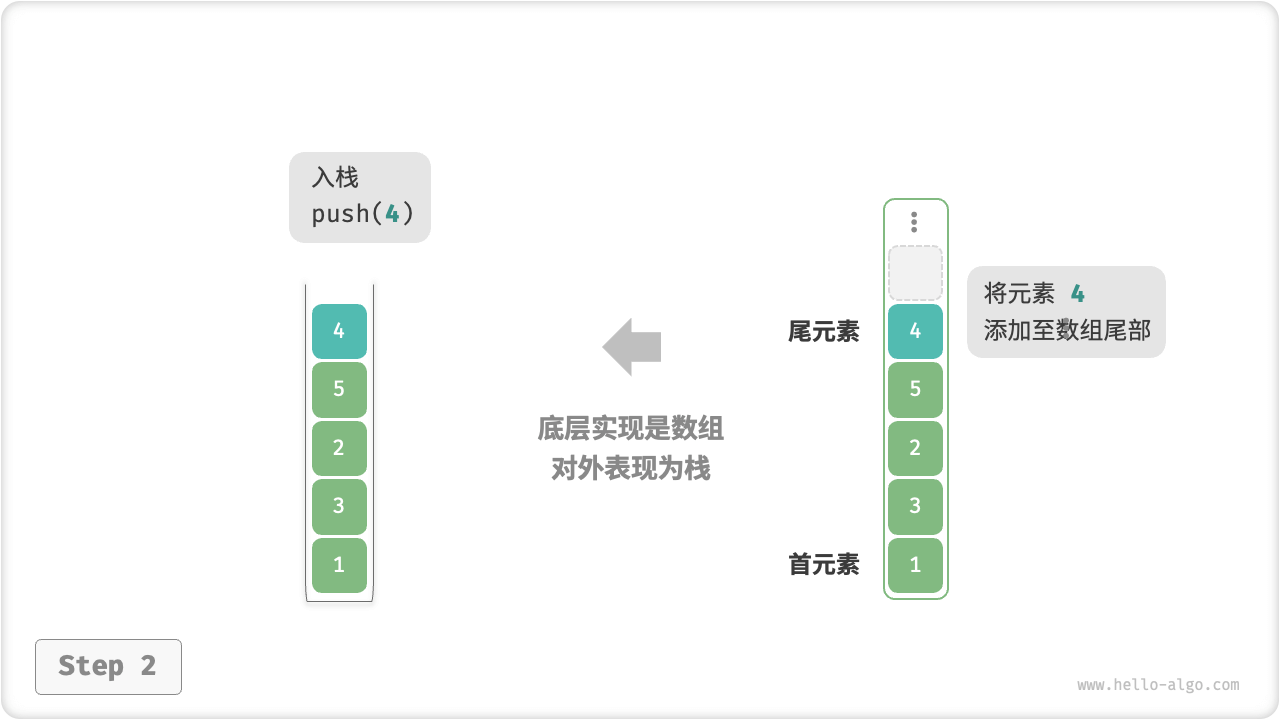
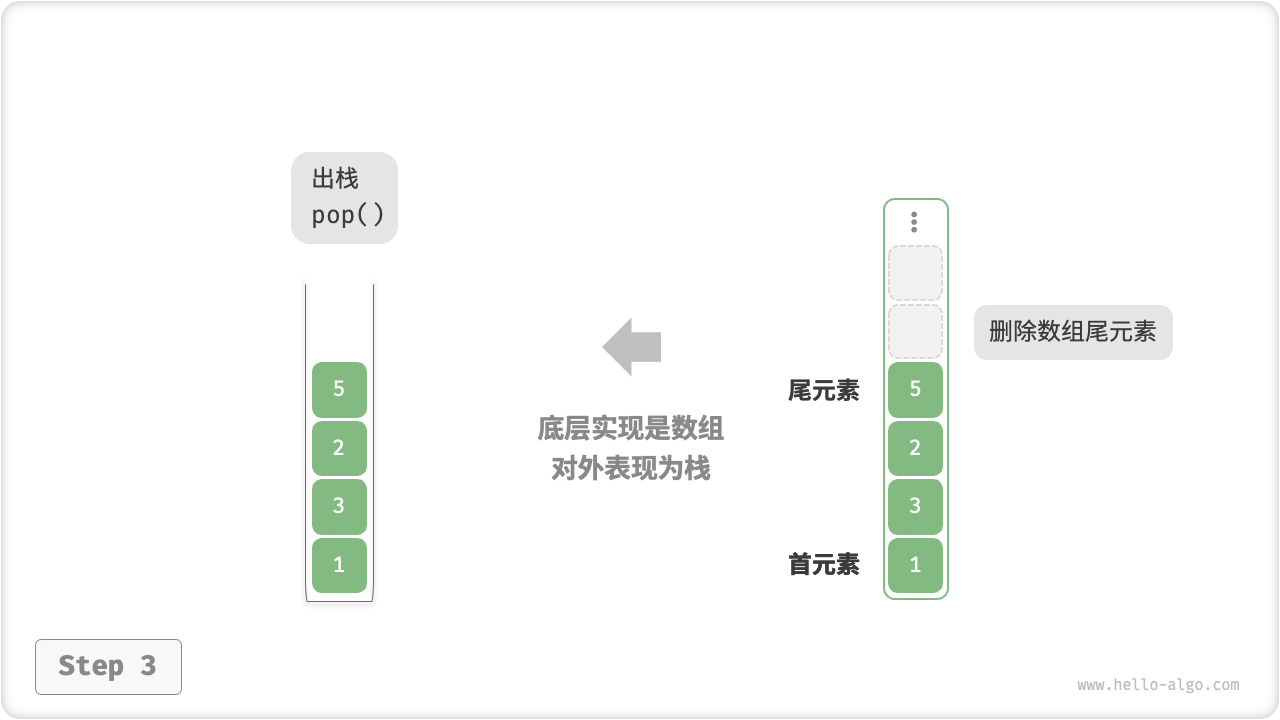
  • 使用数组实现栈时，我们可以将数组的尾部作为栈顶。
  • 如图 5-3 所示，入栈与出栈操作分别对应在数组尾部添加元素与删除元素

（1）基于数组图解

  • ArrayStack

基于数组实现栈的入栈出栈操作

  • push()

array_stack_push

  • pop()

array_stack_pop

（2）基于数组代码

  • 由于入栈的元素可能会源源不断地增加，因此我们可以使用动态数组，这样就无须自行处理数组扩容问题。
class ArrayStack:
    """基于数组实现的栈"""

    def __init__(self):
        """构造方法"""
        self._stack: list[int] = []

    def size(self) -> int:
        """获取栈的长度"""
        return len(self._stack)

    def is_empty(self) -> bool:
        """判断栈是否为空"""
        return self._stack == []

    def push(self, item: int):
        """入栈"""
        self._stack.append(item)

    def pop(self) -> int:
        """出栈"""
        if self.is_empty():
            raise IndexError("栈为空")
        return self._stack.pop()

    def peek(self) -> int:
        """访问栈顶元素"""
        if self.is_empty():
            raise IndexError("栈为空")
        return self._stack[-1]

    def to_list(self) -> list[int]:
        """返回列表用于打印"""
        return self._stack

【5】栈典型应用

  • 浏览器中的后退与前进、软件中的撤销与反撤销。每当我们打开新的网页，浏览器就会将上一个网页执行入栈，这样我们就可以通过后退操作回到上一页面。后退操作实际上是在执行出栈。如果要同时支持后退和前进，那么需要两个栈来配合实现。
  • 程序内存管理。每次调用函数时，系统都会在栈顶添加一个栈帧，用于记录函数的上下文信息。在递归函数中，向下递推阶段会不断执行入栈操作，而向上回溯阶段则会执行出栈操作。

【三】用代码实现堆和栈

【1】堆

# 堆的操作是先进先出（FIFO）
list_queue = []
for i in range(0, 5):
    print(f'{i} 已入堆(队列)')
    list_queue.append(i)
print('------入堆完毕--------')
while list_queue:
    print(f'{list_queue.pop(0)} 已出堆(队列)')
print('------出堆完毕--------')

0 已入堆(队列)
1 已入堆(队列)
2 已入堆(队列)
3 已入堆(队列)
4 已入堆(队列)
------入堆完毕--------
0 已出堆(队列)
1 已出堆(队列)
2 已出堆(队列)
3 已出堆(队列)
4 已出堆(队列)
------出堆完毕--------

【2】栈

# 栈的操作是先进后出（LIFO）
list_stack = []
for i in range(0, 5):
    print(f'{i} 已入栈')
    list_stack.append(i)
print('------入栈完毕--------')
while list_stack:
    print(f'{list_stack.pop()} 已出栈')
print('------出栈完毕--------')

0 已入栈
1 已入栈
2 已入栈
3 已入栈
4 已入栈
------入栈完毕--------
4 已出栈
3 已出栈
2 已出栈
1 已出栈
0 已出栈
------出栈完毕--------

【四】可变数据类型

  • 对于可变类型（如列表、字典等），在函数中修改参数会影响原始对象。

img

【1】字典

dic = {'name': 'Dream', 'sex': 'male', 'age': 18}

print(id(dic))  # 1499123688064

# 修改字典中的值
dic['age'] = 19
print(dic)  # {'name': 'Dream', 'sex': 'male', 'age': 19}

print(id(dic))  # 1499123688064

# 对字典进行操作时，值改变的情况下，字典的id也是不变，即字典也是可变数据类型

【2】元祖

t1 = ("tom", "jack", [1, 2])
t1[0] = 'TOM'  # 报错：TypeError
t1.append('lili')  # 报错：TypeError

# 元组内的元素无法修改，指的是元组内索引指向的内存地址不能被修改
t1 = ("tom", "jack", [1, 2])
print(id(t1[0]), id(t1[1]), id(t1[2]))
# 2387573744432 2387573821232 2387573821824

# 如果元组中存在可变类型，是可以修改，但是修改后的内存地址不变
t1[2][0] = 111
print(t1)  # ('tom', 'jack', [111, 2])

print(id(t1[0]), id(t1[1]), id(t1[2]))  # 查看id仍然不变
# 2387573744432 2387573821232 2387573821824

【3】列表

list1 = ['tom', 'jack', 'Dream']
print(id(list1))  # 2640601108864

list1[2] = 'kevin'
print(id(list1))  # 2640601108864

list1.append('lili')
print(id(list1))  # 2640601108864

# 对列表的值进行操作时，值改变但内存地址不变，所以列表是可变数据类型

【4】布尔类型

is_right = True
print(id(is_right))  # 140709061454696

is_right = True
print(id(is_right))  # 140709061454696

# 内存地址不改变，说明布尔类型是可变数据类型

【5】集合类型

my_set = {1, 2, 3}
print(id(my_set))  # 1267008236768

# 添加元素
my_set.add(4)
print(id(my_set))  # 1267008236768

# 删除元素
my_set.remove(2)
print(id(my_set))  # 1267008236768

# 内存地址不改变，说明集合类型是可变数据类型

【五】不可变数据类型

  • 对于不可变类型（如数值、字符串等），在函数中修改参数不会影响原始对象。

img

【1】字符串

name = "Dream"
print(id(name))  # 1751102989232

name = "Hope"
print(id(name))  # 1751103065904

# 内存地址改变了，说明字符串是不可变数据类型

【2】数字类型

age = 18
print(id(age))  # 3179829658384

age = 20
print(id(age))  # 3179829658448

# 内存地址改变了，说明数字类型是不可变数据类型

【六】Python是值传递还是引用传递

【1】Python的传递规则

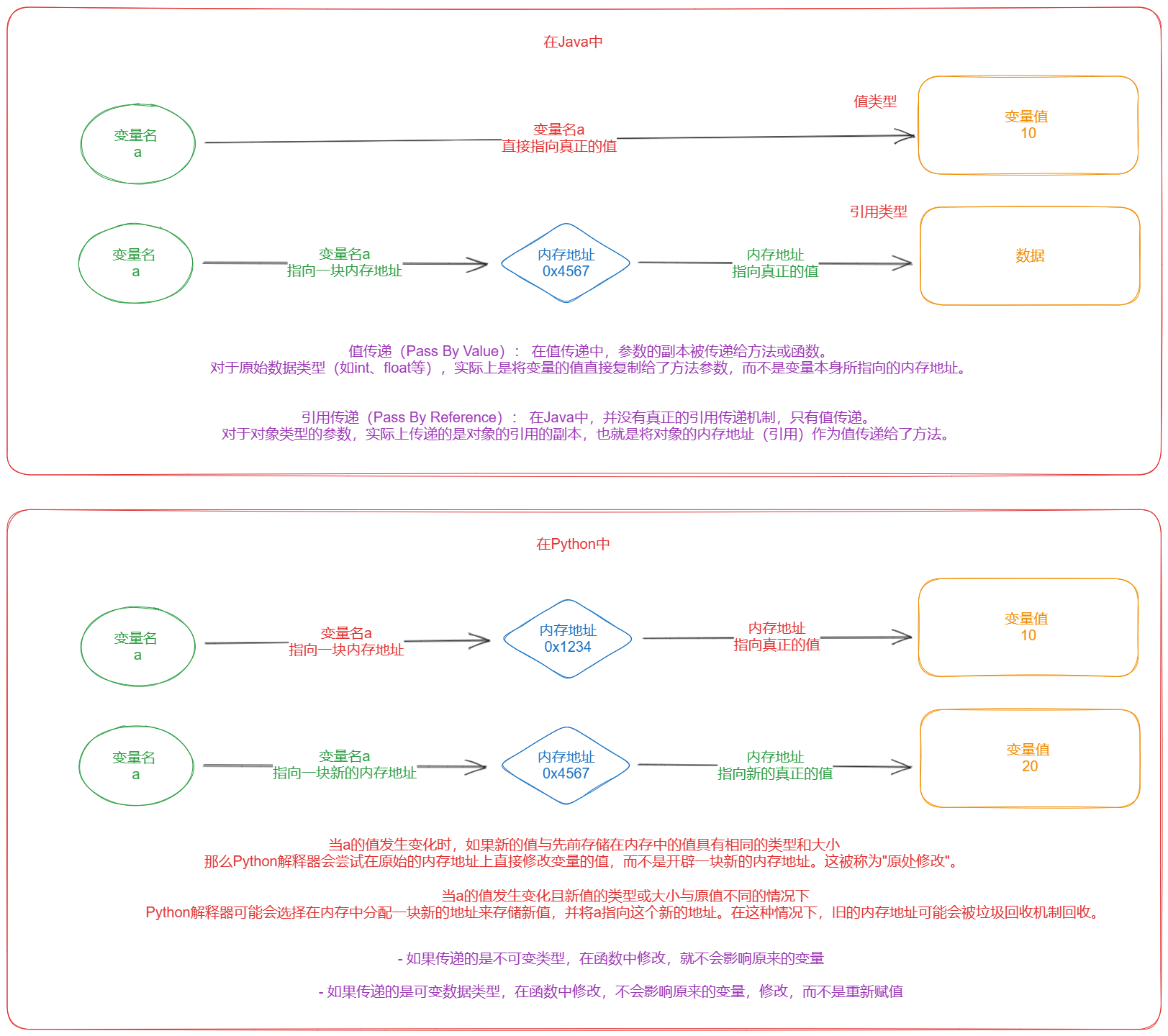
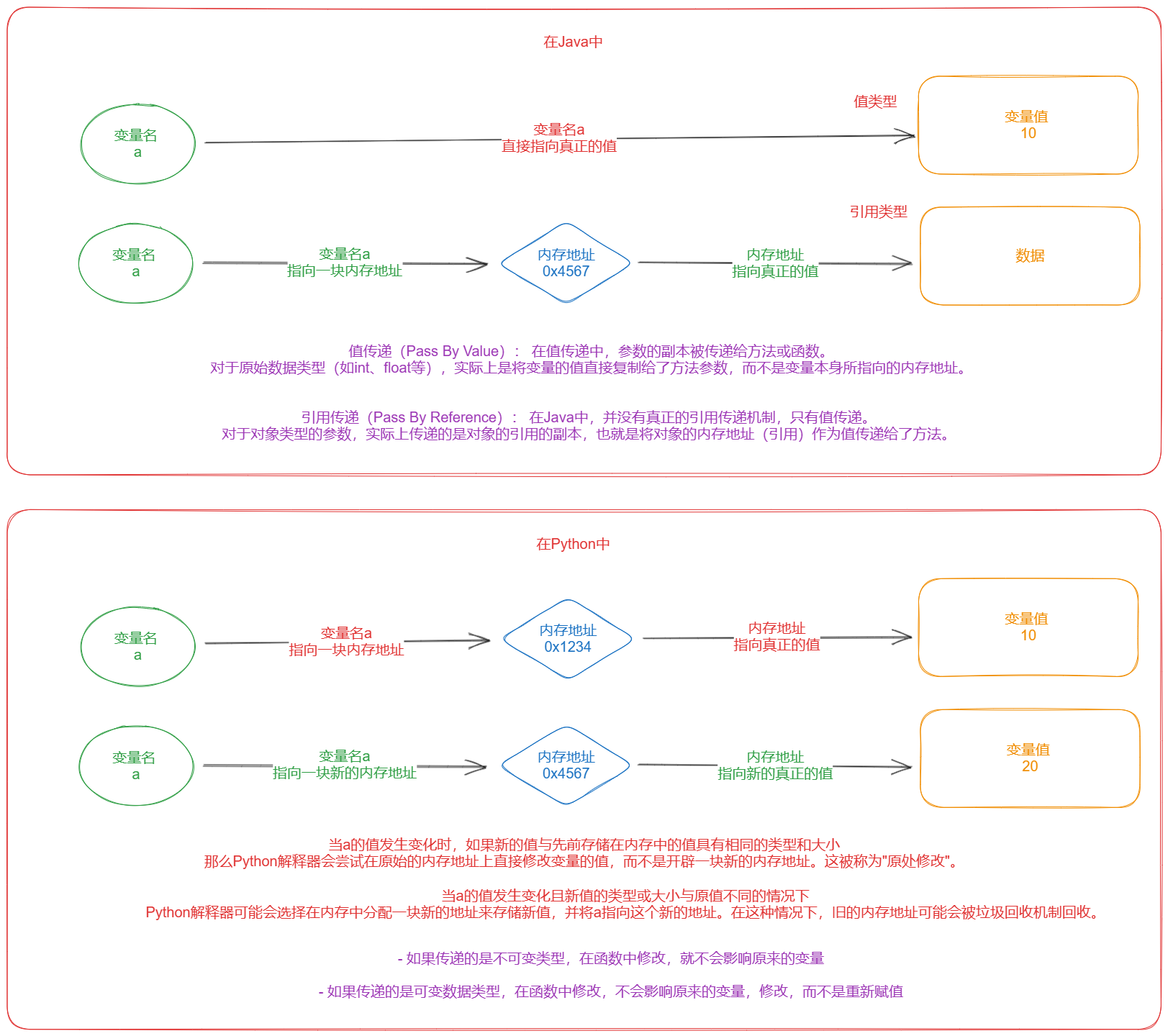
  • 严格意义上来说，Python既不是值传递，也不是引用传递，python是自己的传递方式
  • 规则是：
    • 如果传递的是不可变类型，在函数中修改，就不会影响原来的变量
    • 如果传递的是可变数据类型，在函数中修改，不会影响原来的变量，修改，而不是重新赋值

【2】什么是值，什么是引用

  • 值就是一个变量=具体的值(一块内存空间放着这个变量的值)
  • 引用是一个变量=内存地址(内存地址指向了值)
  • 所有python才有了可变和不可变类型

【3】什么是值传递 什么是引用传递

  • 如果是值传递，函数中修改了传递的值，不会影响原来的
  • 如果是引用传递，函数中修改了传递的引用，就会影响原来的

【4】可变类型的参数传递

  • 对于可变类型（如列表、字典等），在函数中修改参数会影响原始对象。

【5】不可变类型的参数传递

  • 对于不可变类型（如数值、字符串等），在函数中修改参数不会影响原始对象。

标签：Python,数据类型,self,元素,11.0,int,print,节点,def
From： https://www.cnblogs.com/dream-ze/p/17840569.html

相关文章

  • 【10.0】Python基础之数据类型的内置方法
    【一】数据类型内置方法介绍数据类型是用来记录事物状态的，而事物的状态是不断变化的(如:一个人年龄的增长（操作int类型）单个人名的修改（操作str类型），学生列表中增加学生（操作list类型）等)，这意味着我们在开发程序时需要频繁对数据进行操作为了提升我们的开发效率python针对这些常用......
  • 【9.0】Python基础之流程控制语句
    【一】流程控制语句介绍程序是由语句构成，而流程控制语句是用来控制程序中每条语句执行顺序的语句。可以通过控制语句实现更丰富的逻辑以及更强大的功能。几乎所有编程语言都有流程控制语句，功能也都基本相似。其流程控制方式有顺序结构分支结构循环结构这里最简单......
  • Python复制表格文件的指定行：不同的行复制不同次数
      本文介绍基于Python语言，读取Excel表格文件数据，并将其中符合我们特定要求的那一行加以复制指定的次数，而不符合要求的那一行则不复制；并将所得结果保存为新的Excel表格文件的方法。  这里需要说明，在我们之前的文章Python自动复制表格文件中指定的数据行的方法中，也介绍过实现类......
  • python 根据绝对路径关闭进程
    importosimportpsutil#如果未知路径且写入了配置环境#os.system("taskkill/f/imexcel.exe&taskkill/f/imwps.exe")#cmdtaskkill直接输入不需加双引号#cmdtaskkill无法根据绝对路径关闭程序无论有没有双引号(无效查询或没有找到进程)#True,False,N......
  • 根据绝对路径 python 后台打开程序
    importsubprocess#不适用于关闭程序/进程#subprocess.run#等候运行结束#returncode=0,stdout='',stderr=''#后台运行,避免阻塞#避免shell注入gongji#os.system需要双引号(以避免空格),subprocess不需要#cmd直接输入路径如果存在空格需要双引号#retur......
  • Python如何使用Networkx实现复杂的人物关系图？
    (Python如何使用Networkx实现复杂的人物关系图？)1简单引入日常工作、生活中我们经常会遇到一些复杂的事务关系，比如人物关系，那如何才能清楚直观的看清楚这些任务关系呢？比如我们从网上搜索1个人物关系图，大家看看：声明：以下图片来源于网络，如果涉及版权问题，请联系作者删除。本文仅......
  • Conda管理Python版本
    查看Python版本查看当前环境的Python版本condaactivate&&python-V查看指定环境condaactivatetest&&python-V创建Python环境先搜索conda有哪些python版本condasearch--full--namepython根据搜索出来的版本安装condacreate--nametestpython=3.9.7或......
  • 【小沐学Python】Web服务器搭建（Nginx、IIS）
    1、Web服务器web服务器一词可以代指硬件或软件，或者是它们协同工作的整体。6、NginxNginx是一款自由的、开源的、高性能的HTTP服务器和反向代理服务器，同时也是一个IMAP、POP3、SMTP代理服务器，多用于高连接并发。6.1简介https://nginx.org/en/Nginx是lgorSysoev为俄罗斯......
  • Python | Opencv的人脸检测和人类识别
    ✅作者简介：热爱科研的算法开发者，Python、Matlab项目可交流、沟通、学习。......
  • python 赋值、浅拷贝、深拷贝的区别
    b=a: 赋值引用，a和b都指向同一个对象。b=a.copy(): 浅拷贝,a和b是一个独立的对象，但他们的子对象还是指向统一对象（是引用）。b=copy.deepcopy(a): 深度拷贝,a和b完全拷贝了父对象及其子对象，两者是完全独立的。对于可变的序列，切片操作符:是浅拷贝 比如：a=b[:]......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99