最小生成树 PRIM算法 - 附可运行代码

学习的时候，觉得这篇资料蛮好的：

https://www.cnblogs.com/JayShao/p/12381830.html

然后这篇文章比较新颖，自觉比较适合写代码的理解：

https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/

代码也比较齐全，我自己动手试试吧！

Prim：生成过程中，Edge 必然连着

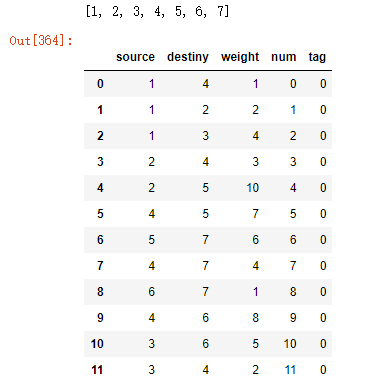
source = [4,1,1,2,2,5,5,7,7,6,6,4]
destiny = [1,2,3,4,5,4,7,4,6,4,3,3]
weight = [1,2,4,3,10,7,6,4,1,8,5,2]


# -- 这个是错误解答： PRIM 用 AOV 试试
tmp_graph = pd.DataFrame()
tmp_graph['source'] = source
tmp_graph['destiny'] = destiny
tmp_graph['weight'] = weight
tmp_graph['num'] = tmp_graph.index
tmp_graph['tag'] = 0

基础准备函数

# ----------
# -- Prim 
# ----------
# -- SWAP
def swap_val(a, b):
    tmp = a; a = b; b = tmp;
    return a,b


# -- 改成无向图
def graph_order(g_in):
    for i in range(len(g_in)):
        if (g_in['source'][i]>g_in['destiny'][i] ):
            g_in['source'][i], g_in['destiny'][i] = swap_val(g_in['source'][i], g_in['destiny'][i])  # 一定要用return
    return g_in


# -- Minimum - return num
def find_min_weight(g_in):
    # -- renew
    tmp_g = g_in.reset_index(drop=True)
    tmp_min = tmp_g['weight'][0]
    tmp_min_ind = tmp_g['num'][0]
    
    for i in range(1,len(tmp_g)):
        if (tmp_g['weight'][i] < tmp_min):
            tmp_min = tmp_g['weight'][i] 
            tmp_min_ind = tmp_g['num'][i]
    
    return tmp_min, tmp_min_ind


# -- 初始排序
tmp_graph = graph_order(tmp_graph)


# ------ 获取节点向量
tmp_vertex = list(tmp_graph['source']) + list(tmp_graph['destiny'])
tmp_vertex = list(set(tmp_vertex))
print(tmp_vertex)

tmp_graph

微封装的循环搜索　Prim 算法

复杂　O(n2)

vertex_selected=[1]
edge_weight=[]
tmp_v_ind = 1


# -- End Case
# 1.vertes_selected 维度与原维度一致，显示被选入顺序
# 2.edge_weight 向量维度与原图维度一致，显示 Aggregated Weight
# 3.上述两个向量长度不一致

cnt_tot = len(tmp_graph)

j=0
is_break=0
count=0

while ( len(vertex_selected)<cnt_tot and is_break==0):
    
    tmp_2=pd.DataFrame()
    for i in range(len(vertex_selected)):
        
        # -- 处理 Ind 产生一个内部循环
        ind_select_1 = (tmp_graph['source']==vertex_selected[i])
        ind_select_2 = (tmp_graph['destiny']==vertex_selected[i])
        ind_select_3 = (tmp_graph['tag']==0)        
        
        ind_select=[]
        for k in range(len(ind_select_1)):
            ind_select.append( (ind_select_1[k] or ind_select_2[k]) and ind_select_3[k] )
        
        # print(ind_select)
        tmp_3 = tmp_graph[ind_select]
        
        if (i==0):
            tmp_2 = tmp_3
        else:
            tmp_2 = pd.concat([tmp_2, tmp_3])
    
    if (len(tmp_2)>0):
        
        # -- 找到最小值的 ind  
        min_weight, min_weight_ind = find_min_weight(tmp_2)
        
        # -- 两端 tag == 1
        tmp_graph['tag'][tmp_graph.num == min_weight_ind]=1  
        
        # -- 是否有环路 
        is_source_existed=0
        tmp_dest = tmp_graph['destiny'][min_weight_ind]
        for k2 in range(len(vertex_selected)):
            if (vertex_selected[k2]==tmp_dest):
                is_source_existed = 1
                break
        
        is_destiny_existed=0
        tmp_dest_1 = tmp_graph['source'][min_weight_ind]
        for k3 in range(len(vertex_selected)):
            if (vertex_selected[k3]==tmp_dest_1):
                is_destiny_existed=1
                break
                            
        # -- append 
        if ( is_source_existed==0 or is_destiny_existed==0):
            if (is_source_existed==0):
                vertex_selected.append(tmp_dest)
            else:
                if(is_destiny_existed==0):
                    vertex_selected.append(tmp_dest_1)    
            edge_weight.append(min_weight)  # Prim 生成一颗树
                
        #print("min_weight: ", min_weight, min_weight_ind)
        #print("vertex_selected: ", vertex_selected)
        #print("edge_weight: ", edge_weight)

        j=j+1
        count=count+1
        
    else:
        is_break=1  
    
print("Edge Weight: ", edge_weight, "\n")
print("Vertex Selected in Order: ", vertex_selected, "\n")
print("Number of Vertex in SET：", len(vertex_selected), "\n")

结论：

第一个向量是选入边的权重，该向量的权重之和就是 Spinning Tree 权重之和，向量维度就是边的数量；

第二个向量，是选入点的顺序（ID）。

Kruscal：最小生成树，AOE_sigma 必然最小，生成过程中，Edge 可不连续

并查集：https://www.bilibili.com/video/BV1b7411N798?p=55

王道数据结构，用森林的概念，识别出不同子集。

注意数据结构。