《算法学习专栏》—— DP问题之状态机模型

2023年10月13日

更新于2023年10月13日

一、前言

本栏，为状态机模型，题目主要来源日常，目前主要来源于Acwing的提高课。希望以后做到状态机的题目，也能加进来，不断完善。使用的分析方法均为闫式DP分析法。字臭。。。希望能用手写板慢慢写的好看。

二、状态机模型

2.1 对于状态机的考虑

我总会带入背包，就只有选与不选两个状态就很尴尬。。。状态机，感觉更像一种思考方式，对于阿福来说，每家店有抢和不抢，对于股票每一天都存在有股票和没股票的一天。这个只能多做，多练习。

2.2 解决的问题

1. 股票买卖
2. 结合kmp
3. 结合kmp和ac自动机

三、题目实现

1. Acwing1049 大盗阿福

题目理解

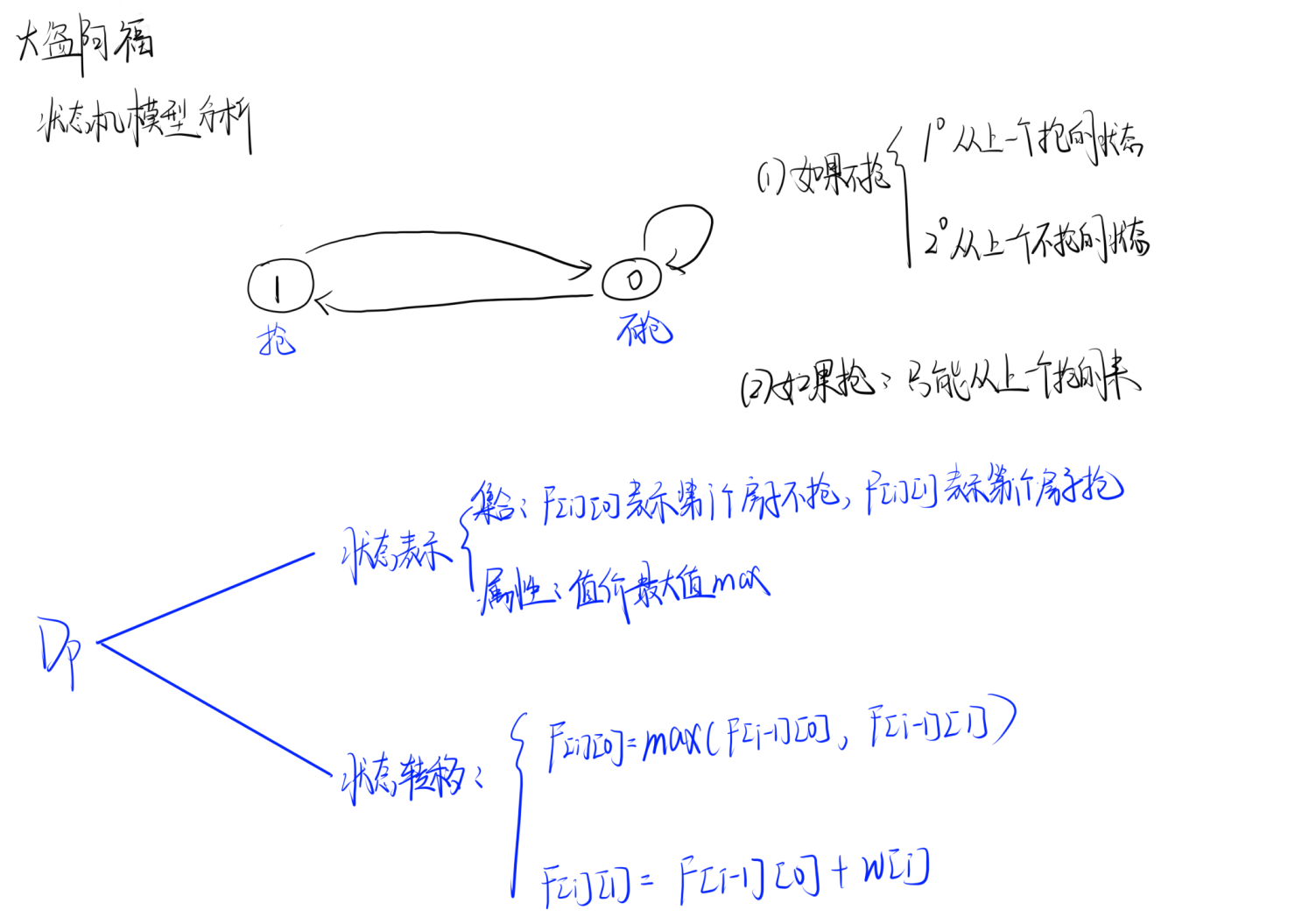
代码实现

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;

int n;
int f[N][2], w[N];

void solve()
{
    memset(f, 0, sizeof f);
    cin >> n;
    
    for(int i = 1; i <= n; i++) cin >> w[i];
    f[0][0] = 0, f[0][1] = -1;
    for(int i = 1; i <= n; i++)
    {
        f[i][0] = max(f[i - 1][0], f[i - 1][1]);
        f[i][1] = f[i - 1][0] + w[i];
    }
    
    cout << max(f[n][0], f[n][1]) << endl;
    return;
}

int main()
{
    int t;
    cin >> t;
    while(t--) solve();
}

2. Acwing1057 股票买卖Ⅳ

题目理解

这个图里，忘记减W[i]了，尴尬

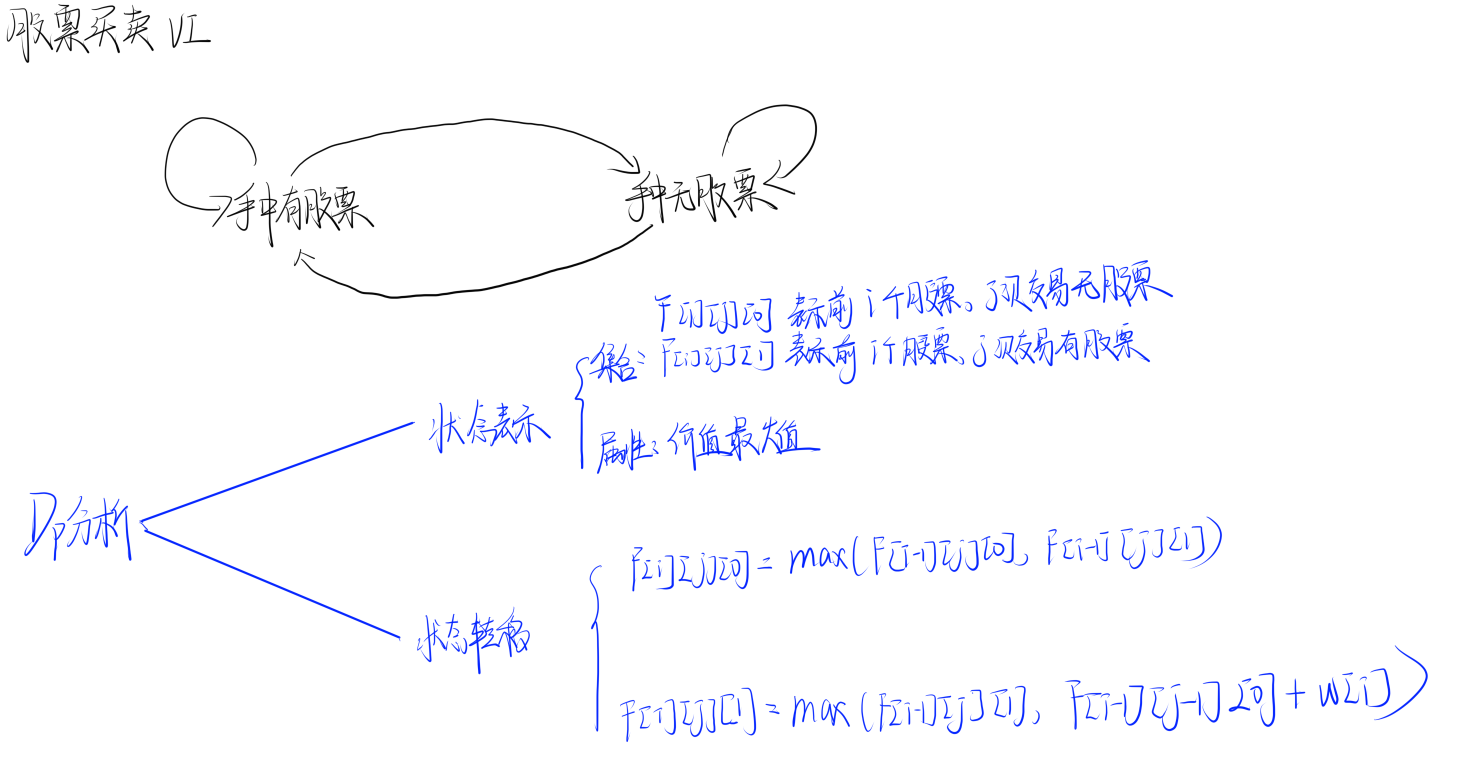
代码实现

int n, m;
int f[N][110][3], w[N];

void solve()
{
    cin >> n >> m;
    
    for(int i = 1; i <= n; i++) cin >> w[i];
    
    // init
    memset(f, -0x3f3f3f3f, sizeof f);
    
    for(int i = 0; i <= n; i++) f[i][0][0] = 0;

    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        {
            f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w[i]);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
        }
    
    int res = 0;
    for(int i = 1; i <= m; i++)
        res = max(res, f[n][i][0]);
    cout << res << endl;
    return;
}

3. Acwing1058 股票买卖Ⅴ

题目理解

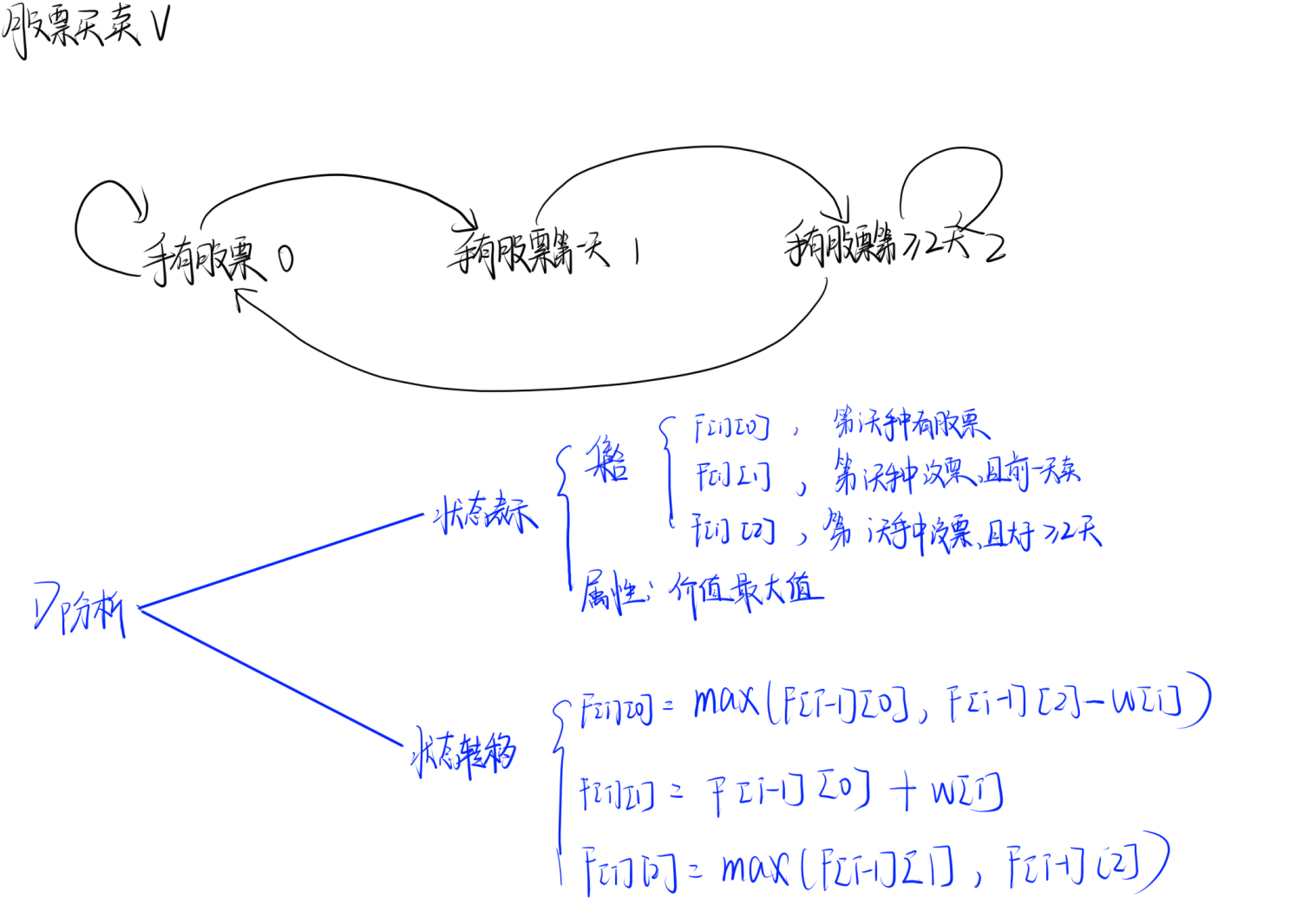
代码实现

int w[N], f[N][3];

int main()
{
    
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> w[i];
    
    f[0][2] = 0;
    f[0][1] = f[0][0] = -0x3f3f3f3f;
        
    for(int i = 1; i <= n; i++)
    {
        f[i][0] = max(f[i - 1][0], f[i - 1][2] - w[i]);
        f[i][1] = f[i - 1][0] + w[i];
        f[i][2] = max(f[i - 1][1], f[i - 1][2]);
    }
    
    cout << max(f[n][1], f[n][2]);
    return 0;
}