二分查找中的mid+1和mid-1的问题
二分查找中的边界问题处理不好很容易导致死循环和计算错误的问题,以题目 数的范围为例。
- 题目大意
二分查找重复数第一次出现的位置和最后一次出现的位置。
- 数学含义
第一次位置即 找到 一个长度最大的 >=X 区间的 左边界
最后一次位置即 找到一个长度最大的 >= X 区间的右边界
注意 找的目标是左边界或者右边界 不是找整个区间
-
图形示意
L=左边界 R=有边界 M=中间值(所选比较的数)T=目标位置
M的意义在于通过缩小区间 找到位置T
 image-20230905221643547
image-20230905221643547 -
重要结论
重要的一步是将M的值传递出去时候,即 L=M 或者R = M,即把目标范围的左或右边界设置为M。
因为不管是M+1或者是M-1 ,指针都会移动。直接赋值M的时候,指针可能不会移动,就会造成死循环。
具体代码分析
找第一次出现的位置
- 循环结束的条件 L==R,最后一次循环时 L+1==R,即搜索的目标范围内有两个元素。
- M 为L+R的下取整,有可能取到L,不可能取到R,但是赋值是赋给R,即R=L,最终条件 L==R 会结束循环。
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (a[mid] < x) l = mid + 1;
else r = mid;
}
找最后一次出现的位置
-
方法一 以【0,n-1】闭区间,最小搜索范围是2个元素,取右边界
因为M的值是赋给L的,即L=M,所以M不能取到左边界,所以要向上取整。
所谓的闭区间 ,个人理解最后一次循环时只有两个元素,左右指针在这两个数之间移动。
image-20230905224331820
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (a[mid] <= x) l = mid;
else r = mid-1;
}
-
方法二 以【0,n) 左闭右开区间 ,最小搜索范围是3个元素,取中间元素
所谓左闭右开区间,个人理解需要加上循环上的判断控制,才能形成开区间效果,使得最后一次循环时只有三个元素,左右指针在第一、第二个数直接移动。
由于l +1 < r 保证了最小搜索范围是3个元素,所以 l + r >> 1 时M会取到L和R中间的数,不会取L或者R,主要保证不能取到L。
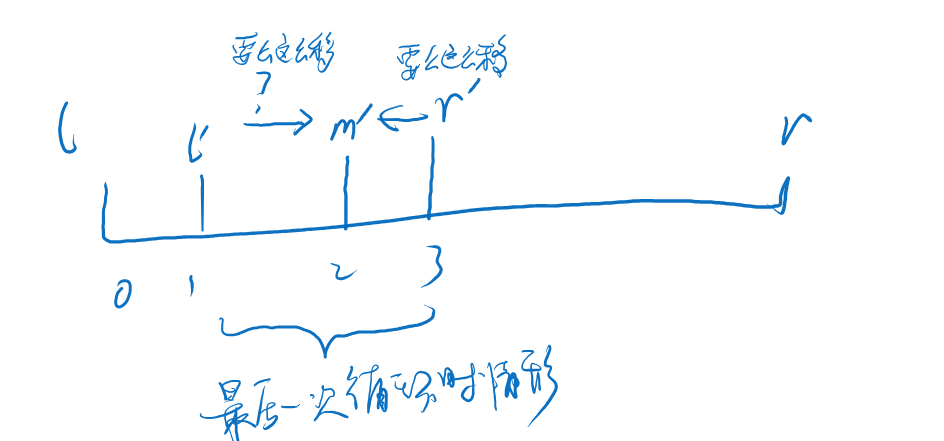 image-20230905225702420
image-20230905225702420
int l = 0, r = n ;
while (l +1 < r) {
int mid = l + r >> 1;
if (a[mid] <= x) l = mid;
else r = mid; // 想想此处可不可以写成 r=mid-1
}
第一次位置 左闭区间0开始
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (a[mid] < x) l = mid + 1;
else r = mid;
}
- 方法三 以(-1,n)左开右开区间
左开是为了求第一次出现位置,同样保证最后一次循环是3个元素, l + r >> 1 时M会取到L和R中间的数,不会取L或者R,主要保证不能取到R,因为找第一次位置主要是将M赋值给R。
第一次位置
int l = -1, r = n - 1;
while (l+1 < r) {
int mid = l + r >> 1;
if (a[mid] < x) l = mid ;
else r = mid;
}
最后一次位置
while (l+1 < r) {
int mid = l + r >> 1;
if (a[mid] <= x) l = mid ;
else r = mid;
}
完整代码
需要注意最后输出
第一次坐标 的二分的边界定为 左边为<X 右边>=X 则所求为R
最后一次坐标的二分边界定位 左边为<=X 右边>X 则所求为L
#include<iostream>
using namespace std;
const int N=1e5+5;
int n,m,q[N];
int main()
{
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++) scanf("%d",&q[i]);
while(m--)
{
int k;scanf("%d",&k);
//寻找第一个等于K的坐标 我这边让二分的边界定为 左边为<5 右边>=5 则所求为r
int l=-1,r=n;
while(l+1<r)//当l与r没有相接的时候,求边界
{
int mid=l+r>>1;
//下面找第一个>=5的坐标
if(q[mid]>=k) r=mid;
else l=mid;
}
//此时得到的r是第一个>=5的坐标
if(q[r]!=k) {
printf("-1 -1\n");
continue;
}
int ll = r,rr = n;
while(ll+1<rr)
{
int mid=ll+rr>>1;
if(q[mid]<=k) ll=mid;
else rr=mid;
}
printf("%d %d\n", r, ll);
}
}
个人心得体会
开区间 其实就是 最小搜索范围是3元素+左右新增点 的方式。这样就避免了L=M或者R=M 的死循环问题。
二分查找中的mid+1和mid-1的问题
二分查找中的边界问题处理不好很容易导致死循环和计算错误的问题,以题目 数的范围为例。
- 题目大意
二分查找重复数第一次出现的位置和最后一次出现的位置。
- 数学含义
第一次位置即 找到 一个长度最大的 >=X 区间的 左边界
最后一次位置即 找到一个长度最大的 >= X 区间的右边界
注意 找的目标是左边界或者右边界 不是找整个区间
-
图形示意
L=左边界 R=有边界 M=中间值(所选比较的数)T=目标位置
M的意义在于通过缩小区间 找到位置T
 image-20230905221643547
image-20230905221643547 -
重要结论
重要的一步是将M的值传递出去时候,即 L=M 或者R = M,即把目标范围的左或右边界设置为M。
因为不管是M+1或者是M-1 ,指针都会移动。直接赋值M的时候,指针可能不会移动,就会造成死循环。
具体代码分析
找第一次出现的位置
- 循环结束的条件 L==R,最后一次循环时 L+1==R,即搜索的目标范围内有两个元素。
- M 为L+R的下取整,有可能取到L,不可能取到R,但是赋值是赋给R,即R=L,最终条件 L==R 会结束循环。
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (a[mid] < x) l = mid + 1;
else r = mid;
}
找最后一次出现的位置
-
方法一 以【0,n-1】闭区间,最小搜索范围是2个元素,取右边界
因为M的值是赋给L的,即L=M,所以M不能取到左边界,所以要向上取整。
所谓的闭区间 ,个人理解最后一次循环时只有两个元素,左右指针在这两个数之间移动。
image-20230905224331820
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (a[mid] <= x) l = mid;
else r = mid-1;
}
-
方法二 以【0,n) 左闭右开区间 ,最小搜索范围是3个元素,取中间元素
所谓左闭右开区间,个人理解需要加上循环上的判断控制,才能形成开区间效果,使得最后一次循环时只有三个元素,左右指针在第一、第二个数直接移动。
由于l +1 < r 保证了最小搜索范围是3个元素,所以 l + r >> 1 时M会取到L和R中间的数,不会取L或者R,主要保证不能取到L。
 image-20230905225702420
image-20230905225702420
int l = 0, r = n ;
while (l +1 < r) {
int mid = l + r >> 1;
if (a[mid] <= x) l = mid;
else r = mid; // 想想此处可不可以写成 r=mid-1
}
第一次位置 左闭区间0开始
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (a[mid] < x) l = mid + 1;
else r = mid;
}
- 方法三 以(-1,n)左开右开区间
左开是为了求第一次出现位置,同样保证最后一次循环是3个元素, l + r >> 1 时M会取到L和R中间的数,不会取L或者R,主要保证不能取到R,因为找第一次位置主要是将M赋值给R。
第一次位置
int l = -1, r = n - 1;
while (l+1 < r) {
int mid = l + r >> 1;
if (a[mid] < x) l = mid ;
else r = mid;
}
最后一次位置
while (l+1 < r) {
int mid = l + r >> 1;
if (a[mid] <= x) l = mid ;
else r = mid;
}
完整代码
需要注意最后输出
第一次坐标 的二分的边界定为 左边为<X 右边>=X 则所求为R
最后一次坐标的二分边界定位 左边为<=X 右边>X 则所求为L
#include<iostream>
using namespace std;
const int N=1e5+5;
int n,m,q[N];
int main()
{
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++) scanf("%d",&q[i]);
while(m--)
{
int k;scanf("%d",&k);
//寻找第一个等于K的坐标 我这边让二分的边界定为 左边为<5 右边>=5 则所求为r
int l=-1,r=n;
while(l+1<r)//当l与r没有相接的时候,求边界
{
int mid=l+r>>1;
//下面找第一个>=5的坐标
if(q[mid]>=k) r=mid;
else l=mid;
}
//此时得到的r是第一个>=5的坐标
if(q[r]!=k) {
printf("-1 -1\n");
continue;
}
int ll = r,rr = n;
while(ll+1<rr)
{
int mid=ll+rr>>1;
if(q[mid]<=k) ll=mid;
else rr=mid;
}
printf("%d %d\n", r, ll);
}
}
个人心得体会
开区间 其实就是 最小搜索范围是3元素+左右新增点 的方式。这样就避免了L=M或者R=M 的死循环问题。
标签:二分,边界,int,位置,mid,while,算法,查找,else From: https://www.cnblogs.com/zhaodong462502/p/17724451.html