【数据结构与算法】TypeScript 实现图结构

class Grapg<T> {
  // 用于存储所有的顶点
  verteces: T[] = [];
  // 用于存储所有的边 采用邻接表的形式
  adjList: Map<T, T[]> = new Map();

  // 添加顶点
  addVertex(v: T) {
    this.verteces.push(v);
    // 初始化顶点的邻接表
    this.adjList.set(v, []);
  }

  // 添加边
  addEdge(v: T, w: T) {
    // 有向图 只需要添加单向的边
    this.adjList.get(v)?.push(w);
    // 无向图 需要添加反向的边
    this.adjList.get(w)?.push(v);
  }

  // 打印图
  printEdges() {
    // 遍历所有的顶点
    this.verteces.forEach((vertex) => {
      // 打印顶点和它的邻接表
      console.log(`${vertex} -> ${this.adjList.get(vertex)?.join(' ')}`);
    });
  }

  // 广度优先遍历
  BFS() {
    if (this.verteces.length === 0) return;
    const visited = new Set<T>(); // 用于存储已经访问过的顶点
    visited.add(this.verteces[0]); // 从第一个顶点开始遍历
    const queue = [this.verteces[0]]; // 用于存储待访问的顶点

    // 队列不为空时
    while (queue.length) {
      const v = queue.shift()!; // 取出队列的第一个顶点
      console.log(v); // 打印顶点

      const vEdges = this.adjList.get(v); // 获取该顶点的邻接表
      // 如果没有邻接表 则跳过
      if (!vEdges) continue;
      // 从前往后遍历
      for (const e of vEdges) {
        // 如果没有访问过 就入队列
        if (!visited.has(e)) {
          visited.add(e);
          queue.push(e);
        }
      }
    }
  }

  // 深度优先遍历
  DFS() {
    if (this.verteces.length === 0) return;
    const visited = new Set<T>(); // 用于存储已经访问过的顶点
    visited.add(this.verteces[0]); // 从第一个顶点开始遍历
    const stack = [this.verteces[0]]; // 用于存储待访问的顶点

    // 栈不为空时
    while (stack.length) {
      const v = stack.pop()!; // 取出栈顶的顶点
      console.log(v); // 打印顶点

      const vEdges = this.adjList.get(v); // 获取该顶点的邻接表
      if (!vEdges) return; // 如果没有邻接表 则跳过
      // 从后往前遍历
      for (let i = vEdges.length - 1; i >= 0; i--) {
        const e = vEdges[i]; // 获取顶点
        // 如果没有访问过 就入栈
        if (!visited.has(e)) {
          stack.push(e);
          visited.add(e);
        }
      }
    }
  }
}

const graph = new Grapg<string>();
// 添加A-I的顶点
for (let i = 0; i < 9; i++) {
  graph.addVertex(String.fromCharCode(65 + i));
}
// 添加边
graph.addEdge('A', 'B');
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');
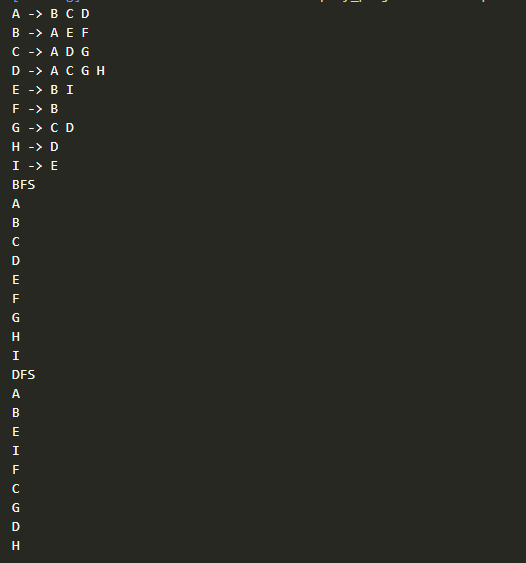
graph.printEdges();
console.log('BFS');
graph.BFS();
console.log('DFS');
graph.DFS();