数据结构与算法 --- 如何分析排序算法

引言

排序算法是最基础的算法，对于排序算法，除学习算法原理，代码实现之外，更重要的是学习每个算法的特点，知道在什么场景下选择那种算法。

那一定是选择时间复杂度最低的排序算法就是最优的吗？

可以从以下几个方面分析一下。

排序算法的执行效率

对于排序算法的执行效率，一般从以下几个方面来分析：

1. 最好时间复杂度，最坏时间复杂度，平均时间复杂度。

   在分析排序算法的时间复杂度时，我们要分别给出最好，最坏，平均情况下的时间复杂度，以及这些不同的复杂度对应的待排序数据的特点。对于排序算法，原始数据的序度（接近有序的程度），对排序的执行时间有很大影响（尤其极端情况）。

2. 时间复杂度的系数，常数和低阶。

   时间复杂度反映的是算法的执行时间随数据规模n的增长趋势，再用大O表示法表示复杂度的时候，通常会省略掉系数，常数和低阶。但是当数据规模很小的时候，系数，常数和低阶的占比很大，也需要考虑。

3. 比较次数或交换（或移动）次数。

   常用的排序算法，如冒泡排序、插入排序、选择排序、快速排序和归并排序等，是基于比较的排序算法，这类排序算法的执行过程设计两个操作：比较元素大小和交换（或移动）元素位置。而这两个操作的耗时是不同的，比较元素大小的耗时要少于交换（或移动）元素位置。所以，在对排序算法的执行效率进行精细化分析时，要把比较次数和交换（或移动）次数区分开来统计。

排序算法的内存消耗

算法的内存消耗可以通过空间复杂度来衡量，排序算法也不例外。除空间复杂度分析之外，根据排序算法是否需要额外的非常量级的数据存储空间，可以分为 原地排序算法（在原数据存储空间上完成排序操作） 和 非原地排序算法（需要额外的非常量级的数据存储空间才能完成排序）。

特别注意的是，原地排序并不与 \(O(1)\) 空间复杂度划等号。

一个排序算法是原地排序算法，可能它的空间复杂度并不是 \(O(1)\) ，但是，一个排序算法的空间复杂度是 \(O(1)\) ，那么它肯定是原地排序算法。

排序算法的稳定性

对于大部分算法，只分析执行效率和内存消耗就足够了，不过，排序算法还有一个特有的分析维度：稳定性，根据稳定性，可以把排序算法分为稳定排序算法和不稳定排序算法。

如果带排序的数据中存在值相等的元素，经过稳定排序算法排序之后，相等元素之间原有的先后顺序不变。经过不稳定排序算法排序之后，相等元素之间原有的先后顺序可能会被改变。

例如，有这样一组数据：2、5、9、3、8、5，按照从小到大的的排序之后就变成了2、3、5、5、8、9。

其中数据中有两个5，那么当经过某种排序算法排序之后，两个5的前后顺序无变化，则该排序算法为稳定排序算法，反之，两个5的前后顺序发生变化，则为不稳定排序算法。

那么就产生了疑问，两个5不是一样的吗？

实际上，为了简化对算法的讲解，我们一般是用整数或字符串这些基本数据类型的数据做算法对象演示，但是在真正开发过程中，要排序的对象往往是复杂的数据类型“对象”，按照“对象”的某个属性（称为算法的Key值）进行排序。因此，尽管两个对象的Key值相同，但他们并不是相同的对象。

例如：现在要对电商系统中的“订单”排序，订单有两个属性，“下单时间”和“订单金额”，如果有10万条数据，我们按照金额从小到大排序，对于金额相同的订单，则按照下单时间从早到晚排序。在怎么做？

最先想到的处理方法：首先按照金额对订单进行排序，然后遍历排序之后的订单，对于每个金额相同的小区间在按照下单时间排序，这种排序思路理解起来很直接，符合常规思维，但是实现起来很繁琐。

再来看看借助稳定排序算法的处理思路。我们先按照下单时间给订单排序，注意是按照下单时间而不是金额。在排序完成之后，在利用稳定排序算法，按照订单金额重新排序。在两遍排序后，就达到了预期要求，但是可能理解需要仔细琢磨。

稳定排序算法可以保持金额相同的两个对象，在排序之后的前后顺序不变，在第一次排序之后，所有的订单按照下单时间从早到晚排序，在第二次排序中，我们用稳定排序算法按照金额排序，相同金额的订单原有的先后顺序不变，仍然保持按照下单时间从早到晚排序，如下图：

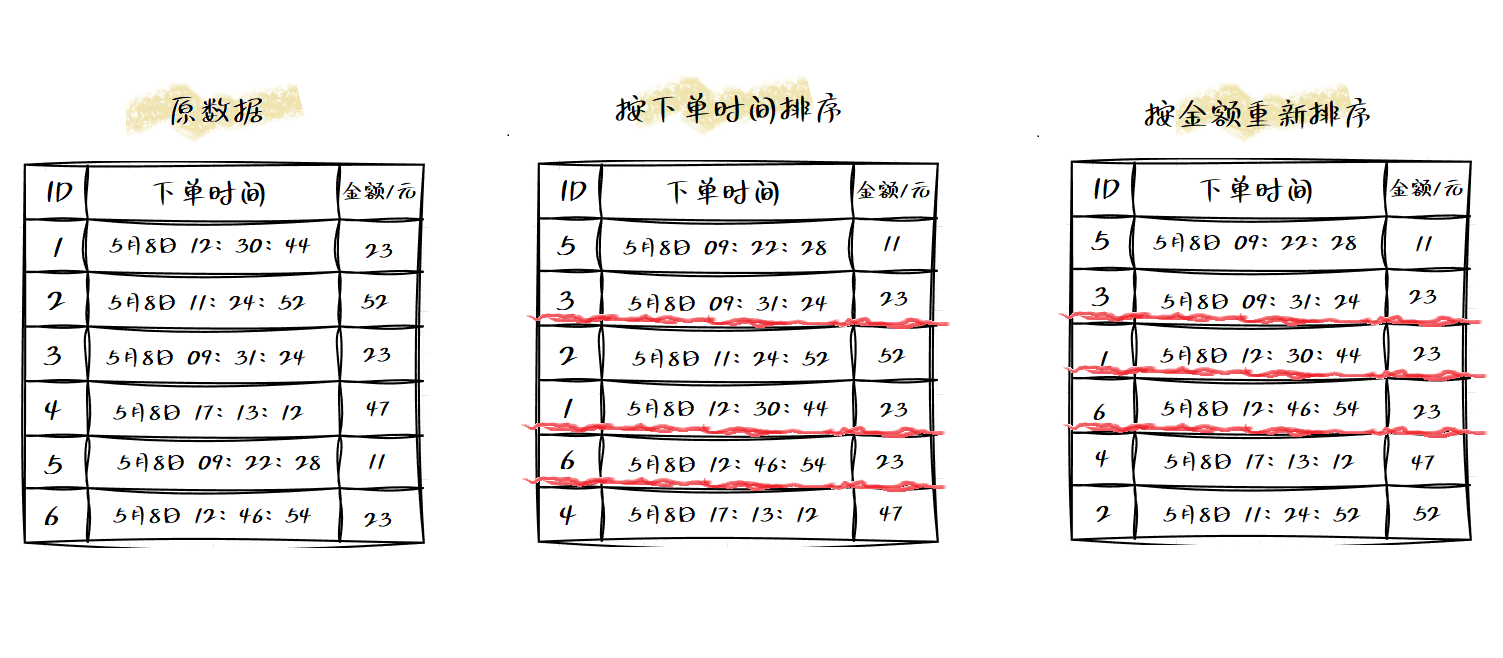
可以看出第一次按下单时间排序后，金额为23元的三个订单ID按顺序分别是3、1、6，经过第二次排序之后他们的订单ID按顺序依旧是3、1、6。

参考资料

[1] 数据结构与算法之美 / 王争 著. --北京：人民邮电出版社，2021.6