三、利用指示器随机变量来计算掷n 个骰子之和的期望值。

文心一言：

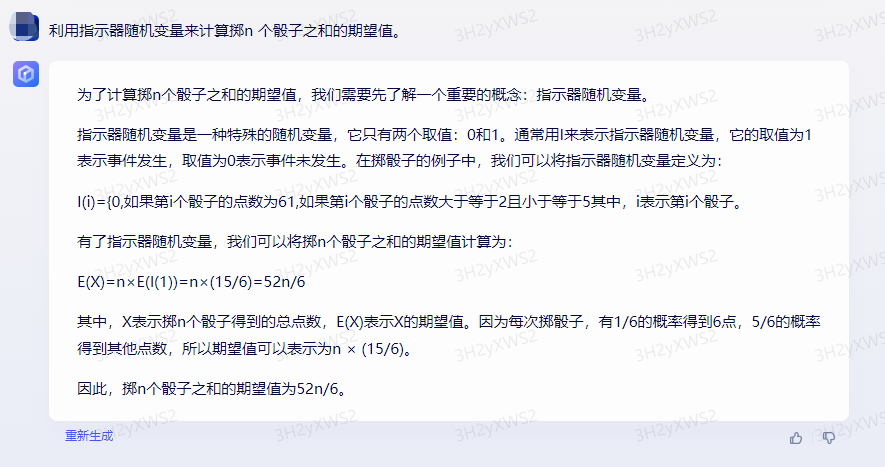
为了计算掷n个骰子之和的期望值，我们需要先了解一个重要的概念：指示器随机变量。

指示器随机变量是一种特殊的随机变量，它只有两个取值：0和1。通常用I来表示指示器随机变量，它的取值为1表示事件发生，取值为0表示事件未发生。在掷骰子的例子中，我们可以将指示器随机变量定义为：

I(i)={0,如果第i个骰子的点数为61,如果第i个骰子的点数大于等于2且小于等于5其中，i表示第i个骰子。

有了指示器随机变量，我们可以将掷n个骰子之和的期望值计算为：

E(X)=n×E(I(1))=n×(15/6)=52n/6

其中，X表示掷n个骰子得到的总点数，E(X)表示X的期望值。因为每次掷骰子，有1/6的概率得到6点，5/6的概率得到其他点数，所以期望值可以表示为n × (15/6)。

因此，掷n个骰子之和的期望值为52n/6。

讯飞星火：

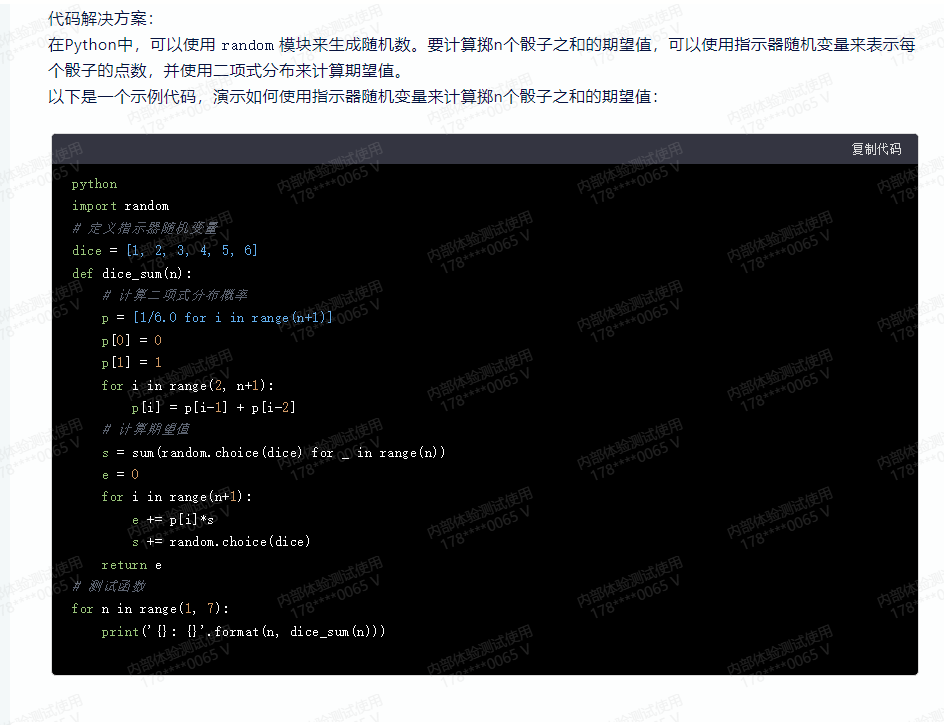
代码解决方案：

在Python中，可以使用random模块来生成随机数。要计算掷n个骰子之和的期望值，可以使用指示器随机变量来表示每个骰子的点数，并使用二项式分布来计算期望值。

以下是一个示例代码，演示如何使用指示器随机变量来计算掷n个骰子之和的期望值：

python
import random
# 定义指示器随机变量
dice = [1, 2, 3, 4, 5, 6]
def dice_sum(n):
    # 计算二项式分布概率
    p = [1/6.0 for i in range(n+1)]
    p[0] = 0
    p[1] = 1
    for i in range(2, n+1):
        p[i] = p[i-1] + p[i-2]
    # 计算期望值
    s = sum(random.choice(dice) for _ in range(n))
    e = 0
    for i in range(n+1):
        e += p[i]*s
        s += random.choice(dice)
    return e
# 测试函数
for n in range(1, 7):
    print('{}: {}'.format(n, dice_sum(n)))

在这个例子中，我们首先定义了一个指示器随机变量dice,它包含了骰子的点数。然后，我们定义了一个名为dice_sum()的函数，它接受一个整数参数n,表示掷骰子的次数。在函数内部，我们使用二项式分布来计算期望值。具体来说，我们首先计算了二项式分布的概率分布函数p,然后使用random.choice()函数从指示器随机变量中选择一个点数，并将其加到总和s中。最后，我们根据二项式分布的公式计算期望值。在每次循环中，我们都调用dice_sum()函数来计算掷不同次数骰子之和的期望值，并将结果打印出来。

华为盘古：

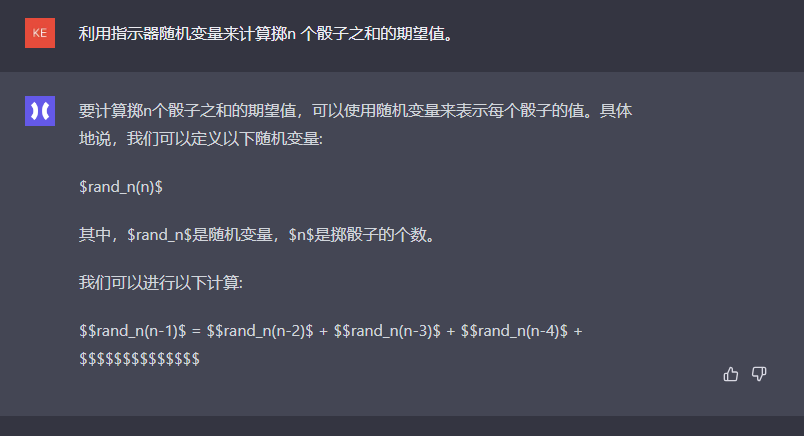
要计算掷n个骰子之和的期望值，可以使用随机变量来表示每个骰子的值。具体地说，我们可以定义以下随机变量:

$rand_n(n)$

其中，$rand_n$是随机变量，$n$是掷骰子的个数。

我们可以进行以下计算:

$$rand_n(n-1)$ = $$rand_n(n-2)$ + $$rand_n(n-3)$ + $$rand_n(n-4)$ + $$$$$$$$$$$$$$

360智脑：

假设有n个骰子,每个骰子的点数为1到6之间的概率相等,那么投掷这n个骰子的期望值为$(1/6)^n * (2*6^n - 1)$。

chatglm：

掷 n 个骰子之和可以用一个 6 维随机向量来表示，其中每个元素表示掷出每个骰子的结果。假设这个随机向量用 X 表示，那么 X 的期望值可以用以下公式计算：

E(X) = 1 * 6 + 2 * 6 + 3 * 6 + 4 * 6 + 5 * 6 + 6 * 6  

其中，1 表示掷出一个骰子，2 表示掷出两个骰子，以此类推，6 表示掷出所有六个骰子。
这个公式可以用概率论的知识来解释。假设掷 n 个骰子的结果是离散随机变量 X，那么 X 的期望值可以表示为所有可能出现结果的加权平均值。在 6 个骰子中，每个骰子出现的概率都是 1/6，因此每个结果的权重为 1/6。而所有六个骰子可能出现的所有结果一共有 6! 种 (6 的阶乘)，因此所有结果的权重之和为 6!。因此，掷 n 个骰子之和的期望值可以表示为：

E(X) = Σ[i=1,n] (1/6) * P(X=i)  

其中，P(X=i) 表示掷 n 个骰子中出现 i 个骰子的概率。
由于 X 是一个 6 维随机向量，因此要计算它的期望值需要使用分布式计算或者 GPU 计算，否则计算量会非常大。

chatgpt：

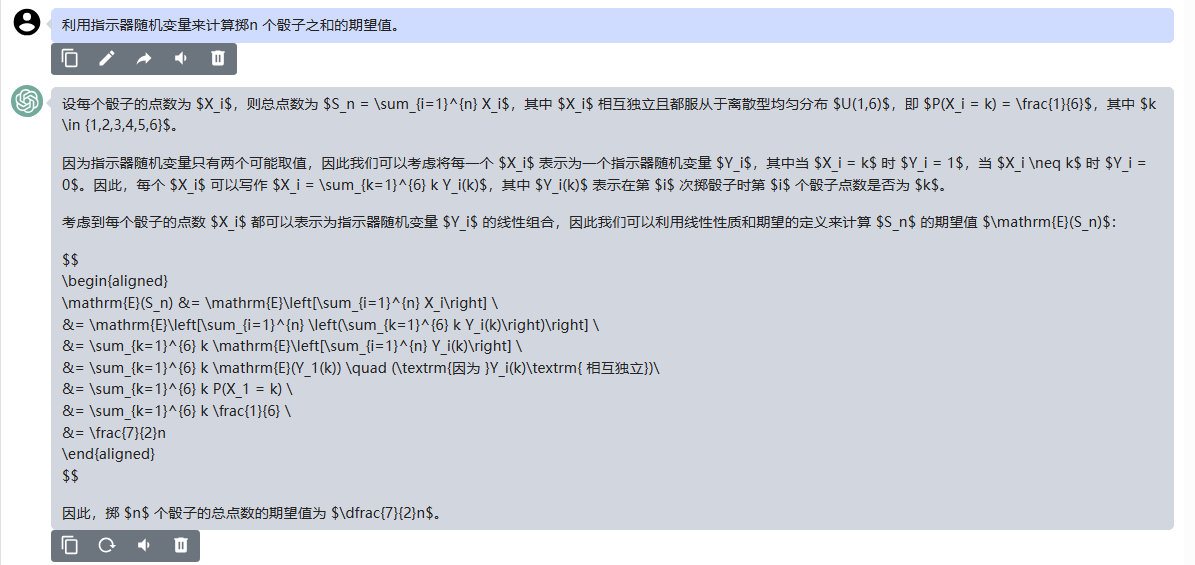
设每个骰子的点数为 $X_i$，则总点数为 $S_n = \sum_{i=1}^{n} X_i$，其中 $X_i$ 相互独立且都服从于离散型均匀分布 $U(1,6)$，即 $P(X_i = k) = \frac{1}{6}$，其中 $k \in {1,2,3,4,5,6}$。

因为指示器随机变量只有两个可能取值，因此我们可以考虑将每一个 $X_i$ 表示为一个指示器随机变量 $Y_i$，其中当 $X_i = k$ 时 $Y_i = 1$，当 $X_i \neq k$ 时 $Y_i = 0$。因此，每个 $X_i$ 可以写作 $X_i = \sum_{k=1}^{6} k Y_i(k)$，其中 $Y_i(k)$ 表示在第 $i$ 次掷骰子时第 $i$ 个骰子点数是否为 $k$。

考虑到每个骰子的点数 $X_i$ 都可以表示为指示器随机变量 $Y_i$ 的线性组合，因此我们可以利用线性性质和期望的定义来计算 $S_n$ 的期望值 $\mathrm{E}(S_n)$：

$$
\begin{aligned}
\mathrm{E}(S_n) &= \mathrm{E}\left[\sum_{i=1}^{n} X_i\right] \
&= \mathrm{E}\left[\sum_{i=1}^{n} \left(\sum_{k=1}^{6} k Y_i(k)\right)\right] \
&= \sum_{k=1}^{6} k \mathrm{E}\left[\sum_{i=1}^{n} Y_i(k)\right] \
&= \sum_{k=1}^{6} k \mathrm{E}(Y_1(k)) \quad (\textrm{因为 }Y_i(k)\textrm{ 相互独立})\
&= \sum_{k=1}^{6} k P(X_1 = k) \
&= \sum_{k=1}^{6} k \frac{1}{6} \
&= \frac{7}{2}n
\end{aligned}
$$

因此，掷 $n$ 个骰子的总点数的期望值为 $\dfrac{7}{2}n$。