标签：10 树莓 plt img 编程 cv2 图像 np import

原文：Raspberry Pi Computer Vision Programming

协议：CC BY-NC-SA 4.0

译者：飞龙

本文来自【ApacheCN 计算机视觉 译文集】，采用译后编辑（MTPE）流程来尽可能提升效率。

当别人说你没有底线的时候，你最好真的没有；当别人说你做过某些事的时候，你也最好真的做过。

六、色彩空间，变换和阈值

在上一章中，我们学习了如何对图像执行基本的数学和逻辑运算。 在本章中，我们将继续探索计算机视觉及其在现实世界中的应用领域中一些更有趣的概念。 就像本书前面的章节一样，我们将在 Python 3 上进行大量动手练习，并创建许多实际的应用。 我们将涵盖计算机视觉领域的许多高级主题。 我们将学习的主要主题与色彩空间，变换和阈值图像有关。 完成本章后，您将能够为一些基本的实际应用编写程序，例如跟踪特定颜色的对象。 您还可以将几何和透视变换应用于图像和实时 USB 网络摄像头。

在本章中，我们将探讨以下主题：

• 色彩空间及其变换
• 对图像执行变换操作
• 图像的透视变换
• 对图像执行阈值

技术要求

可以在 GitHub 上找到本章的代码文件。

观看以下视频，以查看这个页面上的“正在执行的代码”。

色彩空间及其变换

让我们了解色彩空间的概念。 颜色空间是用于表示一组颜色的数学模型。 使用色彩空间，我们可以用数字表示颜色。 如果您曾经使用过 Web 编程，那么您必须遇到各种颜色代码，因为颜色在 HTML 中以十六进制数字表示。 这是一个用颜色空间表示颜色的好例子，并允许我们使用它们执行数值和逻辑计算。 用色彩空间表示颜色还使我们能够轻松地以模拟和数字形式复制颜色。

在本书中，我们将经常使用 BGR，RGB，HSV 和灰度色彩空间。 在 BGR 和 RGB 中，B 代表蓝色，G 代表绿色，R 代表红色。 OpenCV 读取彩色图像并将其存储在 BGR 色彩空间中。 HSV 色彩空间表示一组颜色，其中包含用于色相的成分，用于饱和度的成分和用于值的成分。 它是计算机图形学和计算机视觉领域中非常常用的色彩空间。 OpenCV 具有cv2.cvtColor(img, conv_flag)函数，该函数更改作为参数传递给它的图像的色彩空间。 源和目标色彩空间由传递给conv_flag参数的参数表示。 此函数使用用于色彩空间转换的数学公式将色彩的数值从源色彩空间转换为目标色彩空间。

注意：

您可以通过以下 URL 阅读有关色彩空间和转换的更多信息。

您可能还记得，在第 4 章“计算机视觉入门”中，我们讨论了 OpenCV 以 BGR 格式加载图像，而 Matplotlib 使用 RGB 图片格式。 因此，当我们以 BGR 格式显示 OpenCV 读取的图像，而以 RGB 格式显示 Matplotlib 时，在可视化中红色和蓝色通道会互换，并且图像看起来很有趣。 在使用 Matplotlib 显示图像之前，我们应该将图像从 BGR 转换为 RGB。 有两种方法可以做到这一点。

让我们看看第一种方法。 我们可以将图像分为 B，G 和 R 通道，并使用split()和merge()函数将它们合并为 RGB 图像，如下所示：

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.2.07.tiff', 1)
b,g,r = cv2.split (img)
img = cv2.merge((r, g, b))
plt.imshow (img)
plt.title ('COLOR IMAGE')
plt.axis('off')
plt.show()

但是，拆分和合并操作的计算量很大。 更好的方法是使用cv2.cvtColor()函数将图像的色彩空间从 BGR 更改为 RGB，如以下代码所示：

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.2.07.tiff', 1)
img = cv2.cvtColor (img, cv2.COLOR_BGR2RGB)
plt.imshow (img)
plt.title ('COLOR IMAGE')
plt.axis('off')
plt.show()

在前面的代码中，我们使用cv2.COLOR_BGR2RGB标志进行颜色转换。 OpenCV 有很多这样的颜色转换标志。 我们可以运行以下程序来查看整个列表：

import cv2
j=0
for filename in dir(cv2):
    if filename.startswith('COLOR_'):
        print(filename)
        j = j + 1
print('There are ' + str(j) +
      ' Colorspace Conversion flags in OpenCV '
      + cv2.__version__ + '.')

输出的最后几行显示在以下代码块中（由于空间限制，我不包括整个输出）：

.
.
.
.
.
COLOR_YUV420p2RGBA
COLOR_YUV420sp2BGR
COLOR_YUV420sp2BGRA
COLOR_YUV420sp2GRAY
COLOR_YUV420sp2RGB
COLOR_YUV420sp2RGBA
COLOR_mRGBA2RGBA

OpenCV 4.0.1 中有 274 个色彩空间转换标志。

HSV 色彩空间

术语 HSV 代表色相，饱和度和值。 在此颜色空间或颜色模型中，颜色为，由色相（也称为色调），阴影（其为饱和度标度或表示的灰色量）表示 ]两端的白色和黑色）以及亮度（值或发光度）。 红色，黄色，绿色，青色，蓝色和品红色的强度由色相表示。 术语饱和度是指颜色中存在的灰色成分的数量。 颜色的亮度或强度由值分量表示。

以下代码将颜色从 BGR 转换为 HSV 并进行打印：

import cv2
import numpy as np
c = cv2.cvtColor(np.array([[[255, 0, 0]]],
                          dtype=np.uint8),
                 cv2.COLOR_BGR2HSV)
print(c)

前面的代码段将打印以 BGR 表示的蓝色的 HSV 值。 以下是输出：

[[[120 255 255]]]

在本书中，我们将大量使用 HSV 色彩空间。 在继续进行之前，让我们创建一个带有跟踪栏的小应用，当跟踪器移动时，它会调整颜色的饱和度：

import cv2
def emptyFunction():
    pass
img = cv2.imread('/home/pi/book/dataset/4.2.07.tiff', 1)
windowName = "Saturation Demo"
cv2.namedWindow(windowName)
cv2.createTrackbar('Saturation Level',
                   windowName, 0,
                   24, emptyFunction)
while(True):
    hsv = cv2.cvtColor( img, cv2.COLOR_BGR2HSV)
    h, s, v = cv2.split(hsv)
    saturation = cv2.getTrackbarPos('Saturation Level', windowName)
    s = s + saturation
    v = v + saturation
    img1 = cv2.cvtColor(cv2.merge((h, s, v)), cv2.COLOR_HSV2BGR)
    cv2.imshow(windowName, img1)
    if cv2.waitKey(1) == 27:
        break
cv2.destroyAllWindows()

在前面的代码中，我们首先将图像从 BGR 转换为 HSV，然后将其拆分为 H，S 和 V 分量。 然后，根据跟踪器在跟踪栏中的位置，为饱和度（s）加上值（v）。 然后，我们合并所有通道以创建 HSV 图像，然后将其转换回 BGR 以使用cv2.imshow()函数显示。 以下是输出窗口的屏幕截图：

图 6.1 –用于调整图像饱和度的应用

基于颜色的实时跟踪

现在，让我们学习如何演示转换色彩空间以实现实际迷你项目的概念。 HSV 色彩空间使我们可以轻松处理一定范围的色彩。 要跟踪可以在特定范围内具有颜色的对象，我们需要将图像的色彩空间转换为 HSV，并检查图像的任何部分是否在我们感兴趣的颜色的特定范围内。OpenCV 具有函数cv2.inRange()，它提供了定义颜色范围的功能。

此函数接受图像以及颜色范围的上限和下限作为参数。 然后，它检查给定图像的任何像素是否落在颜色范围内（上限和下限）。 如果图像中的像素值在颜色的给定范围内，则将输出图像中的相应像素设置为0值； 否则，将其设置为255值。 这将创建一个二进制图像，该图像可以用作计算我们将用于跟踪应用的逻辑操作的掩码。

下面的示例演示了此概念。 我们使用逻辑bitwise_and()函数提取我们感兴趣的颜色范围：

import numpy as np
import cv2
cap = cv2.VideoCapture(0)
while ( True ):
    ret, frame = cap.read()
    hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
    image_mask = cv2.inRange(hsv, np.array([40, 50, 50]),
    np.array([80, 255, 255]))
    output = cv2.bitwise_and(frame, frame, mask=image_mask)
    cv2.imshow('Original', frame)
    cv2.imshow('Output', output)
    if cv2.waitKey(1) == 27:
        break
cv2.destroyAllWindows()
cap.release()

在此程序中，我们正在跟踪绿色对象。 输出结果应类似于以下屏幕截图所示。 在这里，我使用了容器的盖子（盖子），它是绿色的：

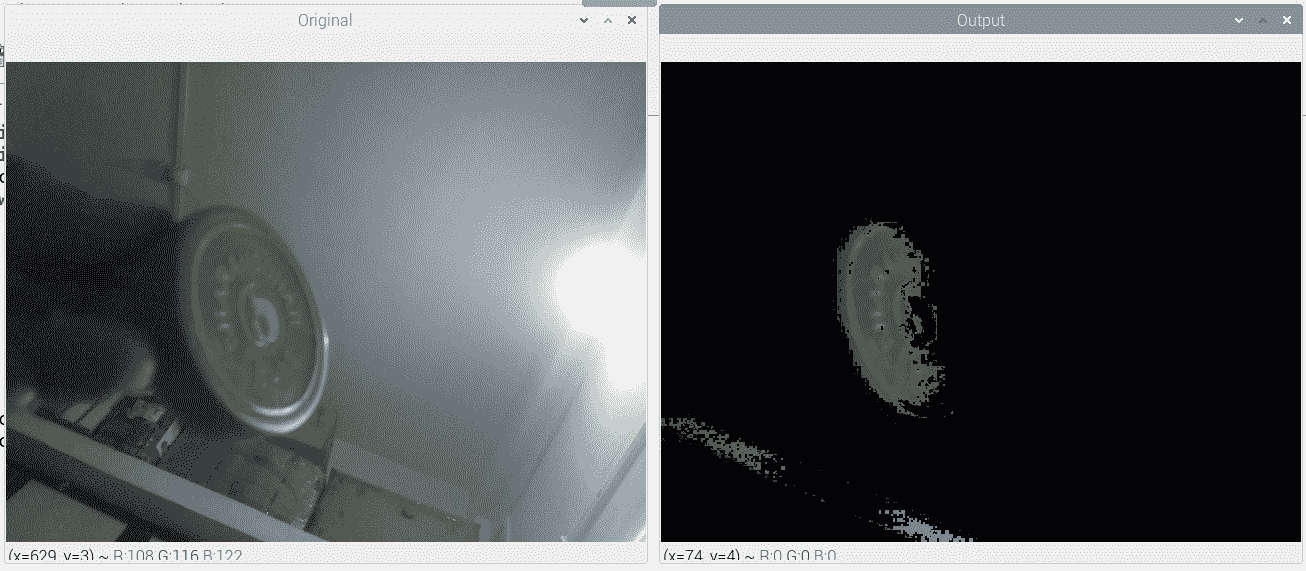
图 6.2 –通过颜色实时跟踪对象

墙壁的各个部分也带有绿色。 因此，它们在输出中也可见。

我没有包括我们在前面的输出中计算出的中间遮罩图像。 通过将以下代码行添加到我们先前编写的代码中，我们可以在单独的输出窗口中查看它：

cv2.imshow('Image Mask', image_mask)

该遮罩是纯黑色的，而是白色的，也称为二进制图像。 如果我们对前面的代码进行修改，我们可以跟踪具有不同颜色的对象。 我们必须为感兴趣的颜色范围创建另一个遮罩。然后，可以将两个遮罩组合起来，如下所示：

blue = cv2.inRange(hsv, np.array([100, 50, 50]), np.array([140, 255, 255]))
green = cv2.inRange(hsv, np.array([40, 50, 50]), np.array([80, 255, 255]))
image_mask = cv2.add(blue, green)
output = cv2.bitwise_and(frame, frame, mask=image_mask)

运行此代码，然后自己检查输出。 我们可以在此代码中添加一个跟踪栏，以选择蓝色或绿色的范围。 以下是执行此操作的步骤：

1. 首先，导入所有必需的库：

   import numpy as np
   

   import cv2
   

2. 然后，我们定义一个空函数：

   def emptyFunction():
   

       pass
   

3. 让我们初始化所有必需的对象和变量：

   cap = cv2.VideoCapture(0)
   

   windowName = 'Object Tracker'
   

   trackbarName = 'Color Chooser'
   

   cv2.namedWindow(windowName)
   

   cv2.createTrackbar(trackbarName,
   

                      windowName, 0, 1,
   

                      emptyFunction)
   

   color = 0
   

4. 在这里，我们有一个主循环：

   while (True):
   

       ret, frame = cap.read()
   

       hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
   

       color = cv2.getTrackbarPos(trackbarName, windowName)
   

       if color == 0:
   

           image_mask = cv2.inRange(hsv, np.array([40, 50, 50]),
   

                                    np.array([80, 255, 255]))
   

       else:
   

           image_mask = cv2.inRange(hsv, np.array([100, 50, 50]),
   

                                    np.array([140, 255, 255]))
   

       output = cv2.bitwise_and(frame, frame, mask=image_mask)
   

       cv2.imshow(windowName, output)
   

       if cv2.waitKey(1) == 27:
   

           break
   

5. 最后，我们摧毁了所有窗口并释放了摄像头：

   cv2.destroyAllWindows()
   

   cap.release()
   

运行前面的代码，然后自己查看输出。 到目前为止，我们已经知道了 GPIO 接口和按钮。 作为练习，请尝试使用按钮实现相同的功能，以便有单独的按钮来跟踪蓝色和绿色。

对图像执行变换操作

在本节中，我们将学习如何使用 OpenCV 和 Python 3 对图像执行各种数学转换操作。

缩放

缩放意味着调整图像大小。 这是一个几何运算。 OpenCV 提供用于执行此操作的函数cv2.resize()。 它接受图像，用于像素插值的方法以及比例因子作为参数，并返回比例图像。 下列方法用于对输出中的像素进行插值：

• cv2.INTER_LANCZOS4：这涉及在8x8像素附近的 Lanczos 插值方法。
• cv2.INTER_CUBIC：这涉及在4x4像素邻域上的双三次插值方法，并且首选用于对图像执行缩放操作。
• cv2.INTER_AREA：这意味着使用像素面积关系进行重采样。 这对于在图像上执行缩小操作是优选的。
• cv2.INTER_NEAREST：这表示最近邻插值的方法。
• cv2.INTER_LINEAR：这表示双线性插值方法。 这是参数的默认参数。

以下示例演示了对图像执行放大和缩小的操作：

import cv2
img = cv2.imread('/home/pi/book/dataset/house.tiff', 1)
upscale = cv2.resize(img, None, fx=1.5, fy=1.5,
                     interpolation=cv2.INTER_CUBIC)
downscale = cv2.resize(img, None, fx=0.5, fy=0.5,
                       interpolation=cv2.INTER_AREA)
cv2.imshow('upscale', upscale)
cv2.imshow('downscale', downscale)
cv2.waitKey(0)
cv2.destroyAllWindows()

在前面的代码中，我们首先在两个轴上放大，然后在两个轴上分别缩小1.5和0.5。 运行前面的代码以查看输出。 另外，作为练习，请尝试传递不同的数字作为缩放因子。

图像的平移，旋转和仿射变换

cv2.warpAffine()函数用于计算输入图像上的平移，旋转和仿射仿射等运算。 它接受输入图像，转换矩阵和输出图像的大小作为参数，然后返回转换后的图像。

注意：

您可以在这个页面上找到有关仿射变换的数学方面的更多信息。

以下示例演示了可用于具有cv2.warpAffine()函数的图像的不同类型的数学转换。 平移操作意味着在 XY 参考平面中更改（更准确地说，是移动）图像的位置。x和y轴上的移位因子可以用二维变换矩阵T表示，如下所示：

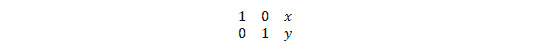
以下代码将图像在 XY 平面中的位置移位(-50, 50)：

import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/house.tiff', 1)
input=cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
rows, cols, channel = img.shape
T = np.float32([[1, 0, -50], [0, 1, 50]])
output = cv2.warpAffine(input, T, (cols, rows))
plt.imshow(output)
plt.title('Shifted Image')
plt.show()

前面的代码的的输出如下：

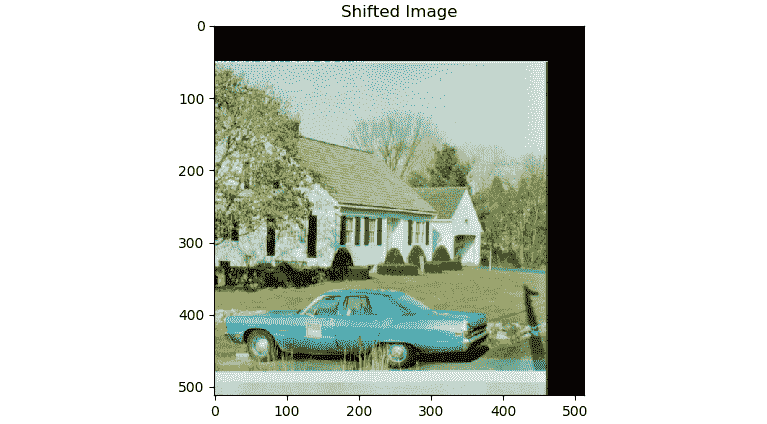
图 6.3 –平移操作的输出

如前面的输出所示，由于输出窗口的大小与输入窗口的相同，因此输出中的一部分图像被裁剪（或截断了），并且原始图像已移出 XY 平面的第一象限。 类似地，我们可以使用cv2.warpAffine()函数将缩放比例的旋转操作应用于输入图像。 对于此演示，我们必须使用cv2.getRotationMatrix2D()函数定义旋转矩阵。

这接受以度为单位的逆时针旋转角度，旋转中心和缩放比例作为参数。 然后，它创建旋转操作的矩阵，该矩阵可以作为参数传递给cv2.warpAffine()函数的调用。 下面的示例将旋转操作应用于输入图像，旋转角度为 45 度，图像中心作为旋转操作的中心，并且还将输出图像缩小到一半（50%） 原始输入图像：

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/house.tiff', 1)
input = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
rows, cols, channel = img.shape
R = cv2.getRotationMatrix2D((cols/2, rows/2), 45, 0.5)
output = cv2.warpAffine(input, R, (cols, rows))
plt.imshow(output)
plt.title('Rotated and Downscaled Image')
plt.show()

输出将为如下：

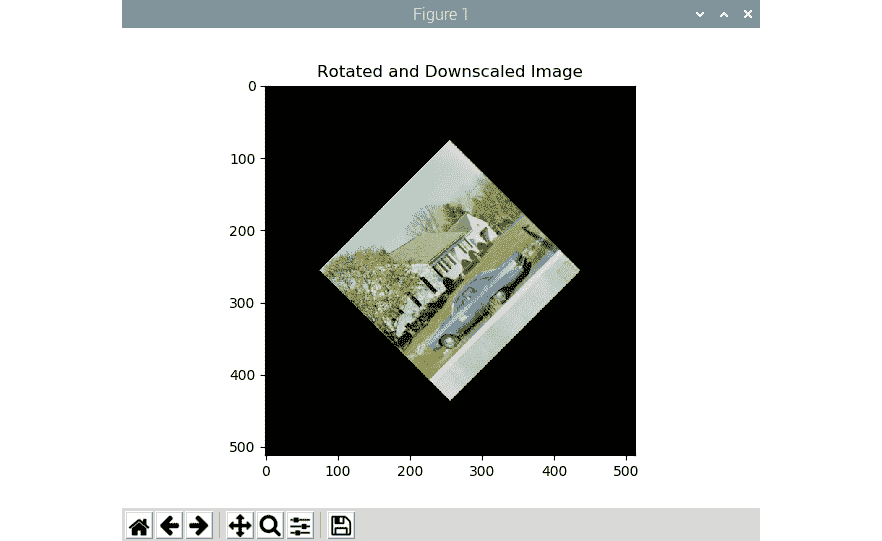
图 6.4 –旋转操作的输出

我们还可以通过修改前面的程序来创建一个非常漂亮的动画。 这里的技巧是，在，循环中，必须以规则的间隔更改旋转角度，并连续显示这些帧以在静止图像上产生旋转效果。 下面的代码示例演示了这一点：

import cv2
from time import sleep
image = cv2.imread('/home/pi/book/dataset/house.tiff',1)
rows, cols, channels = image.shape
angle = 0
while(1):
    if angle == 360:
        angle = 0
    M = cv2.getRotationMatrix2D((cols/2, rows/2), angle, 1)
    rotated = cv2.warpAffine(image, M, (cols, rows))
    cv2.imshow('Rotating Image', rotated)
    angle = angle +1
    sleep(0.2)
    if cv2.waitKey(1) == 27 :
        break
cv2.destroyAllWindows()

运行前面的代码，然后亲自检查的输出。 现在，让我们尝试在实时网络摄像头上实现此技巧。 使用以下代码执行此操作：

import cv2
from time import sleep
cap = cv2.VideoCapture(0)
ret, frame = cap.read()
rows, cols, channels = frame.shape
angle = 0
while(1):
    ret, frame = cap.read()
    if angle == 360:
        angle = 0
    M = cv2.getRotationMatrix2D((cols/2, rows/2), angle, 1)
    rotated = cv2.warpAffine(frame, M, (cols, rows))
    cv2.imshow('Rotating Image', rotated)
    angle = angle +1
    sleep(0.2)
    if cv2.waitKey(1) == 27 :
        break
cv2.destroyAllWindows()

运行前面的代码，看看它的作用。

现在，让我们了解仿射数学变换的概念，并使用 OpenCV 和 Python 3 进行演示。仿射变换是一种几何数学变换，可确保原始输入图像中的平行线在输出图像中保持平行。 仿射变换操作的通常输入是输入图像中不在同一行中的三个点的集合，以及输出图像中不在同一行中的三个点的相应集合。 这些点集将传递给cv2.getAffineTransform()函数以计算转换矩阵，然后将计算出的转换矩阵传递给cv2.warpAffine()调用作为参数。 下面的示例很好地说明了这一概念：

import cv2
import numpy as np
from matplotlib import pyplot as plt
image = cv2.imread('/home/pi/book/dataset/4.2.06.tiff', 1)
input = cv2.cvtColor(image, cv2.COLOR_BGR2RGB )
rows, cols, channels = input.shape
points1 = np.float32([[100, 100], [300, 100], [100, 300]])
points2 = np.float32([[200, 150], [400, 150], [100, 300]])
A = cv2.getAffineTransform(points1, points2)
output = cv2.warpAffine(input, A, (cols, rows))
plt.subplot(121)
plt.imshow(input)
plt.title('Input')
plt.subplot(122)
plt.imshow(output)
plt.title('Affine Output')
plt.show()

之后的是输出：

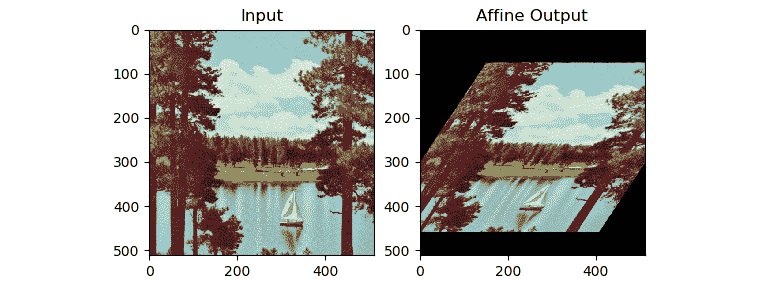
图 6.5 –仿射变换

如我们所见，前面的代码在输入图像上创建了类似剪切的效果。

图像的透视变换

在透视变换的数学运算中，将输入图像中的四个点的集合映射到输出图像中的四个点的集合。 在输入和输出图像中选择四个点的集合的标准是，任何三个点（在输入和输出图像中）不得位于同一行。 与仿射数学变换一样，在透视变换中，输入图像中的直线保持直线。 但是，不能保证输入图像中的平行线在输出图像中保持平行。

这种数学运算的最现实的例子之一是图像编辑和查看软件工具中的缩放和成角度的缩放功能。 缩放的数量和缩放的角度取决于我们前面讨论的两组点所计算出的变换矩阵。 OpenCV 提供cv2.getPerspectiveTransform()函数，该函数从输入图像和输出图像接受两组四个点，并计算转换矩阵。 cv2.warpPerspective()函数接受计算出的矩阵作为参数，并将其应用于输入图像以计算输入图像的透视变换。 以下代码恰当地演示了这一点：

import cv2
import numpy as np
from matplotlib import pyplot as plt
image = cv2.imread('/home/pi/book/dataset/ruler.512.tiff', 1)
input = cv2.cvtColor(image, cv2.COLOR_BGR2RGB )
rows, cols, channels = input.shape
points1 = np.float32([[0, 0], [400, 0], [0, 400], [400, 400]])
points2 = np.float32([[0,0], [300, 0], [0, 300], [300, 300]])
P = cv2.getPerspectiveTransform(points1, points2)
output = cv2.warpPerspective(input, P, (300, 300))
plt.subplot(121)
plt.imshow(input)
plt.title('Input Image')
plt.subplot(122)
plt.imshow(output)
plt.title('Perspective Transform')
plt.show()

输出将显示为，如下所示：

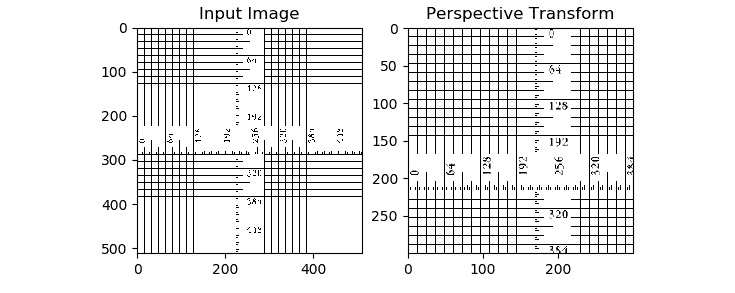
图 6.6 –带有透视变换的缩放操作

作为本节的练习（并加深您对透视变换操作的理解），请将输入和输出图像中点集的各种组合传递给程序，以查看更改输入后输出如何变化。 从我们刚刚讨论的示例中，您可能会得到以下印象：保留了输入图像和输出图像中的线之间的并行性，但这是因为我们为输入图像和输出图像中的点选择了组。 如果我们选择不同的点集，那么输出将明显不同。

这些都是我们可以使用 OpenCV 对图像执行的所有转换操作。 接下来，我们将看到如何使用 OpenCV 对图像进行阈值处理。

对图像应用阈值

阈值是将图像划分为各个部分的最简单方法，这些部分称为段。 阈值化是最简单的分段操作形式。 如果我们将阈值操作应用于灰度图像，通常（但并非始终）将其转换为二进制图像。 二进制图像是严格的黑白图像，像素的值可以为 0（黑色）或 255（白色）。 许多分割算法，高级图像处理操作和计算机视觉应用都将阈值用作处理图像的第一步。

阈值处理可能是最简单的图像处理操作。 首先，我们必须为阈值定义一个值。 如果一个像素的值大于阈值，则将255（白色）分配给该像素； 否则，我们为像素分配0（黑色）。 这是我们可以对图像执行阈值运算的最简单方法。 还有其他阈值处理技术，我们将在本节中学习和演示它们。

OpenCV cv2.threshold()函数将阈值应用于图像。 它接受图像，阈值，最大值和阈值处理技术作为参​​数，并返回阈值图像作为输出。 如果最大值大于阈值，则此函数将最大值分配给像素。 正如我们前面提到的，此方法存在多种变化。 让我们详细了解所有阈值技术。

假设（x，y）是输入像素。 在这里，我们可以通过以下方式对图像进行阈值处理：

• cv2.THRESH_BINARY：如果强度（x，y）>脱粒，则设置强度(x, y) = maxVal； 否则，设置强度(x, y) = 0。
• cv2.THRESH_BINARY_INV：如果强度（x，y）>脱粒，则设置强度(x, y) = 0; 否则，设置强度(x, y) = maxVal。
• cv2.THRESH_TRUNC：如果强度（x，y）>脱粒，然后设置强度（x，y）=阈值； 否则保持强度(x, y)不变。
• cv2.THRESH_TOZERO：如果强度（x，y）>脱粒； 然后保持强度(x, y)不变； 否则，设置强度(x, y) = 0。
• cv2.THRESH_TOZERO_INV：如果强度（x，y）>脱粒，则设置强度(x, y) = 0; 否则，保持强度(x, y)不变。

带有梯度的灰度图像是阈值算法的出色输入，因为我们可以直观地看到实际的阈值。 在以下示例中，我们使用灰度梯度图像作为输入来演示阈值操作。 我们将阈值设置为127，因此根据像素强度的值和我们使用的阈值技术，将图像分为两部分或更多部分：

import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('/home/pi/book/dataset/gray21.512.tiff', 1)
th = 127
max_val = 255
ret, o1 = cv2.threshold(img, th, max_val,
                        cv2.THRESH_BINARY)
print(o1)
ret, o2 = cv2.threshold(img, th, max_val,
                        cv2.THRESH_BINARY_INV)
ret, o3 = cv2.threshold(img, th, max_val,
                        cv2.THRESH_TOZERO)
ret, o4 = cv2.threshold(img, th, max_val,
                        cv2.THRESH_TOZERO_INV)
ret, o5 = cv2.threshold(img, th, max_val,
                        cv2.THRESH_TRUNC)
titles = ['Input Image', 'BINARY', 'BINARY_INV',
          'TOZERO', 'TOZERO_INV', 'TRUNC']
output = [img, o1, o2, o3, o4, o5]
for i in range(6):
    plt.subplot(2, 3, i+1)
    plt.imshow(output[i], cmap='gray')
    plt.title(titles[i])
    plt.axis('off')
plt.show()

以下是的输出：

图 6.7 –阈值运算的输出

您可能要创建一个带有跟踪栏的应用。 我们还可以在上拉配置中连接两个按钮，并通过这两个按钮编写一些代码来调整实时视频的阈值：

import RPi.GPIO as GPIO
import cv2
thresh = 127
cap = cv2.VideoCapture(0)
GPIO.setmode(GPIO.BOARD)
GPIO.setwarnings(False)
button1 = 7
button2 = 11
GPIO.setup(button1, GPIO.IN, GPIO.PUD_UP)
GPIO.setup(button2, GPIO.IN, GPIO.PUD_UP)
while True:
    ret, frame = cap.read()
    button1_state = GPIO.input(button1)
    if button1_state == GPIO.LOW and thresh < 256:
        thresh = thresh + 1
    button2_state = GPIO.input(button2)
    if button2_state == GPIO.LOW and thresh > -1:
        thresh = thresh - 1
    ret1, output = cv2.threshold(frame, thresh, 255,
                           cv2.THRESH_BINARY)
    print(thresh)
    cv2.imshow('Thresholding App', output)
    if cv2.waitKey(1) == 27:
        break
cv2.destroyAllWindows()

通过将两个按钮连接到引脚 7 和 11 来准备电路。将网络摄像头连接到 USB 或 Pi 摄像头模块连接到 CSI 端口。 然后，运行前面的代码。 以下将是输出：

图 6.8 –实时 USB 网络摄像头提要的阈值

输出看起来像这样，因为我们将阈值应用于实时供稿和彩色图像。 OpenCV 将阈值应用于所有通道。 作为练习，将输入帧转换为灰度，然后对其应用不同类型的阈值。

大津的二值化方法

在前面的阈值示例中，我们选择了阈值参数的值。 但是，输入图像阈值的值是通过大津的二值化方法自动确定的。 但是，此方法不适用于所有图像。 前提条件是输入图像在直方图中必须有两个峰。 这样的图像被称为双峰直方图图像。 我们将在本书的后面部分学习有关此概念的更多信息，并演示如何使用直方图和图像的直方图。 双峰直方图通常意味着图像具有背景和前景。大津的二值化最适合此类图像。

除了具有双峰直方图的图像外，不建议使用此方法，因为它会产生不正确的结果。 此方法始终与其他阈值方法结合使用。 在调用cv2.threshold()函数时，我们必须将0作为参数传递给threshold参数，如以下代码片段所示：

ret, output = cv2.threshold(image, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU )

运行前面的代码，然后查看输出。

自适应阈值

在较早的示例（包括大津的二值化）中，整个图像中的所有像素的阈值均相同。 这就是为什么那些技术被称为全局阈值技术。 但是，它们不能对所有类型的图像产生良好的结果。 对于照明不均匀的图像，全局阈值方法不是最佳方法。 我们可以使用根据附近像素的值在本地计算阈值的算法。 这样的技术被称为局部或自适应阈值化技术。

cv2.adaptiveThreshold()方法接受源图像，最大值，自适应阈值方法，阈值算法，块大小和常数作为输入，并生成阈值图像作为输出。 下面显示了如何使用均值和高斯方法确定邻域以确定阈值值：

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.1.05.tiff', 0)
block_size = 123
constant = 6
th1 = cv2.adaptiveThreshold(img, 255,
                            cv2.ADAPTIVE_THRESH_MEAN_C,
                            cv2.THRESH_BINARY,
                            block_size, constant)
th2 = cv2.adaptiveThreshold (img, 255,
                             cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
                             cv2.THRESH_BINARY,
                             block_size, constant)
output = [img, th1, th2]
titles = ['Original', 'Mean Adaptive', 'Gaussian Adaptive']
for i in range(3):
    plt.subplot(1, 3, i+1)
    plt.imshow(output[i], cmap='gray')
    plt.title(titles[i])
    plt.xticks([])
    plt.yticks([])
plt.show()

以下是上述代码的输出：

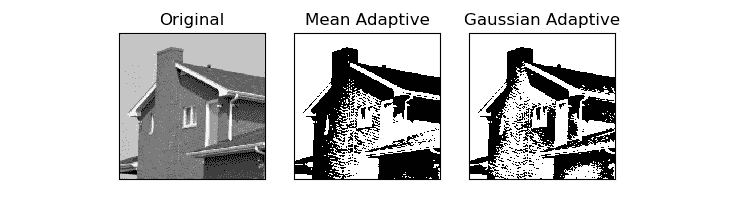
图 6.9 –均值和高斯自适应阈值方法

正如我们在前面的输出图像中看到的那样，平均值和高斯自适应阈值产生的输出是不同的。 我们必须根据输入图像选择适当的阈值算法，以获得所需的结果。 通常，试错方法是选择阈值算法和阈值的最佳方法。

总结

这是有趣的一章。 我们首先查看色彩空间及其用于按颜色跟踪对​​象的应用。 然后，我们了解了转换和阈值设置。 我们还学习了如何使用按钮创建实时阈值的小型应用。 我们展示的所有概念，特别是阈值技术，对于本书稍后将要学习的高级图像处理应用将非常有用。

在下一章中，我们将学习一些信号处理概念和图像噪声。 我们将学习过滤图像和消除图像中噪声的技术。 我们还将这些概念与 RPi 的 GPIO 结合在一起，并创建一些不错的实时图像处理应用。

七、让我们发出一些声音

在上一章中，我们学习并演示了色彩空间的概念及其转换，数学变换和阈值运算。

在本章中，我们将学习和演示与噪声和滤波有关的概念。 整章致力于详细了解噪声的概念。 首先，我们将学习如何深度模拟各种类型的噪声模式。 然后，我们将学习并演示如何使用图像核和卷积运算。 我们还将学习如何使用卷积运算来应用各种类型的过滤器。 最后，我们将学习低通过滤器的基础知识，并演示如何使用它们执行模糊和噪声消除操作。

我们还将使用 GPIO 进行演示。 在本章中，我们将介绍以下主题：

• 噪声
• 使用核
• 使用 SciPy 中的信号处理模块进行 2D 卷积
• 使用 OpenCV 过滤和模糊

完成本章后，您将可以处理嘈杂的图像并减少其中的噪点。

技术要求

可以在 GitHub 上找到本章的代码文件。

观看以下视频，以查看这个页面上的“正在执行的代码”。

噪音

让我们详细了解噪声的概念。 在信号处理领域，噪声仅仅是与期望信号混合的任何不想要的信号。 当我们谈论图像或视频中的噪声时，可以将噪声定义为像素强度和颜色的不希望有的变化。 这种噪声可能来自多个来源。

一些示例包括相机镜头上的灰尘，胶卷中的颗粒（在模拟摄影和胶卷制作中很需要这种颗粒），CCD 传感器及其存储中的错误，发送和接收期间的错误以及扫描照片时的错误。 不需要非常高的噪声。 这是因为高噪声会减少有用和预期的信号，从而影响图像质量。

我们可以用以下公式数学表示信噪比：

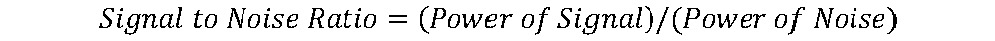
注意：

较高的信噪比意味着有关信号和图像的更好的质量。

向图像引入噪点

如上一节所述，可能有多个噪声源。 我们还可以通过模拟各种类型的噪声将噪声引入数字图像。 在本节中，我们将学习如何模拟椒盐噪声，高斯噪声，泊松噪声和随机法线噪声。

椒盐噪声

在任何图像中随机引入白色（盐）像素和黑色（胡椒粉）像素称为椒盐噪声。 我们可以将其介绍给任何灰度图像，如下所示：

import numpy as np
import cv2
import random
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.1.03.tiff', 0)
output = np.zeros(img.shape, np.uint8)
p = 0.05
for i in range (img.shape[0]):
    for j in range(img.shape[1]):
        r = random.random()
        if r < p/2:
            output[i][j] = 0
        elif r < p:
            output[i][j] = 255
        else:
            output[i][j] = img[i][j]
plt.imshow(output, cmap='gray')
plt.title('Salt and Pepper Sprinkled')
plt.axis('off')
plt.show()

在前面的代码中，噪声密度（由p表示）设置为0.05。 我们为每个像素生成一个随机数，如果它小于p / 2，则将像素设置为黑色。 如果它介于p / 2和p之间，则将像素设置为白色。 否则，像素不会被修改。 由于我们使用random.random()函数生成噪声，因此每次执行程序时生成的噪声都是不同的。 引入了噪声的输出如下所示：

图 7.1 –盐和胡椒粉噪声

我们可以创建一个小型应用，使用实时网络摄像头馈送中的按钮来调整自定义引入的噪声。 现在，在上拉模式下将两个按钮连接到 RPi 的 7 和 11 GPIO 引脚，并编写以下程序：

import RPi.GPIO as GPIO
import cv2
import numpy as np
import random
p = 0.00
cap = cv2.VideoCapture(0)
ret, frame = cap.read()
output = np.zeros(frame.shape, np.uint8)
GPIO.setmode(GPIO.BOARD)
GPIO.setwarnings(False)
button1 = 7
button2 = 11
GPIO.setup(button1, GPIO.IN, GPIO.PUD_UP)
GPIO.setup(button2, GPIO.IN, GPIO.PUD_UP)

在前面的代码中，我们正在初始化 RPi 的 GPIO，并且还将为 USB 网络摄像头创建对象。 现在，让我们编写逻辑来调整按下按钮时得到的噪声量：

while True:
    ret, frame = cap.read()
    button1_state = GPIO.input(button1)
    if button1_state == GPIO.LOW and p <= 0.1:
        p = p + 0.01
    if p > 0.1:
        p = 0.1
    button2_state = GPIO.input(button2)
    if button2_state == GPIO.LOW and p > 0:
        p = p - 0.01
    if p < 0:
        p = 0
    for i in range (frame.shape[0]):
        for j in range(frame.shape[1]):
            r = random.random()
            if r < p/2:
                output[i][j] = 0, 0, 0
            elif r < p:
                output[i][j] = 255, 255, 255
            else:
                output[i][j] = frame[i][j]
    print(p)
    cv2.imshow('Salt and pepper Noise App', output)
    if cv2.waitKey(1) == 27:
        break
cap.release()
cv2.destroyAllWindows()

前面的程序在计算上很昂贵，因为我们正在连续计算噪声和输出图像。 如果您遇到低帧速率，请降低连接到 RPi 的 USB 网络摄像头的分辨率。 代码的输出将类似于上图所示。

高斯噪声

这种噪声以数学家卡尔·弗里德里希·高斯的名字命名，因为噪声的值呈正态分布（也称为高斯分布）。 我们可以模拟这种类型的噪声，如下所示：

import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.1.03.tiff', 0)
row, col = img.shape
img = img.astype(np.float32)
mean = 0
var = 0.1
sigma = var**0.5
gauss = np.random.normal(mean, sigma, (row, col))
gauss = gauss.reshape(row, col)
noisy = img + gauss
print(abs(noisy-img))
plt.imshow(noisy, cmap='gray')
plt.title('Gaussian (Normally distributed) Noise')
plt.axis('off')
plt.show()

前面的代码在灰度图像上分别模拟 0 和1的均值和方差的高斯噪声。 我们首先将图像从uint8转换为float32，因为噪声点可能具有浮点值。 我们正在使用np.random.normal()函数来计算噪声的数据点。 请注意，它产生的噪声量取决于均值和方差的值。 对于我们使用的值，噪声对我们而言是不可感知的。 运行代码并查看输出。 将如下所示：

图 7.2 –高斯（正态分布）噪声

泊松噪声

根据泊松曲线分布的噪声称为泊松噪声。 也称为散粒噪声。 发生此现象是由于光中的粒子性质。 让我们看一些示例代码，其中我们将泊松噪声引入图像：

import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.1.03.tiff', 0)
img = img.astype(np.float32)
vals = len(np.unique(img))
vals = 2 ** np.ceil(np.log2(vals))
noisy = np.random.poisson(img * vals) / float(vals)
print(abs(noisy-img))
plt.imshow(noisy, cmap='gray')
plt.title('Poisson Noise')
plt.axis('off')
plt.show()

np.random.poisson()函数产生沿泊松曲线分布的随机数据点。 这些数据点将添加到图像中，以创建具有泊松噪声的噪点图像。 运行前面的代码并查看输出。 将如下所示：

图 7.3 –泊松噪声

随机正态噪声

我们已经看到了一个高斯正态噪声的例子。 我们还可以生成随机的正态噪声，如下所示：

import numpy as np
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.1.03.tiff', 0)
img = img.astype(np.float32)
row, col = img.shape
rand_noise = np.random.randn(row, col)
rand_noise = rand_noise.reshape(row, col)
noisy = img + img * rand_noise
print(abs(noisy-img))
plt.imshow(noisy, cmap='gray')
plt.title('Random Normal Noise')
plt.axis('off')
plt.show()

在前面的代码中，NumPy np.random.randn()函数创建随机噪声的数据点，然后将其添加到图像中。 这将产生带有随机噪声的图像。 运行前面的代码并查看输出。 将如下所示：

图 7.4 –泊松噪声

使用核

现在，让我们学习有关核的。 我们将学习如何使用核进行信号和图像处理操作。 核是平方数值矩阵。 根据核的大小和组件，如果将核与图像进行卷积，则会得到模糊或锐化的输出。 核用于各种图像处理操作。

让我们看一个用于平均的简单核的示例。 可以用以下公式表示：

通过使用前面的公式，大小为3x3的平均核可以表示为：

行数和列数的值始终为奇数且始终相同。 它们都是正方形矩阵。

我们可以使用下面的 NumPy 代码创建前面的核：

K = np.ones((3, 3), np.uint8)/9

现在，我们将学习如何使用前面的核和其他核来处理数据集中的样本图像。

使用 SciPy 中的信号处理模块的 2D 卷积

现在，让我们看一下卷积的数学背景。 卷积就是在理解一个函数的形状如何受到另一个函数的影响。 计算它的过程和所得函数被称为卷积。 我们可以对 1D，2D 和多维数据进行卷积。 信号是多维实体。 图像是一种信号。 因此，我们可以将卷积应用于图像。

注意

您可以在这个页面上了解有关卷积的更多信息。

我们可以对具有各种核的图像执行卷积运算以处理图像。 为此，我们将学习如何使用 SciPy 的signal模块。 让我们使用以下命令安装 SciPy 库：

pip3 install scipy

我们可以对具有各种核的图像执行卷积运算以处理图像。 对 2D 数据执行卷积的函数是signal.convolve2d()。 我们必须传递一个灰度图像和一个核作为参数，然后计算给定数据的卷积。 以下是一个示例：

import scipy.signal
import numpy as np
import matplotlib.pyplot as plt
import cv2
img = cv2.imread('/home/pi/book/dataset/4.1.03.tiff', 0)
k1 = np.ones((7, 7), np.uint8)/49
blurred = scipy.signal.convolve2d(img, k1)
k2 = np.array([[0, -1, 0],
                   [-1, 25, -1],
                   [0, -1, 0]], dtype=np.int8)
sharpened = scipy.signal.convolve2d(img, k2)
plt.subplot(131)
plt.imshow(img, cmap='gray')
plt.title('Original Image')
plt.axis('off')
plt.subplot(132)
plt.imshow(blurred, cmap='gray')
plt.title('Blurred Image')
plt.axis('off')
plt.subplot(133)
plt.imshow(sharpened, cmap='gray')
plt.title('Sharpened Image')
plt.axis('off')

输出如下：

图 7.5 –使用核执行操作

正如预期的那样，模糊核产生了模糊的输出，锐化核产生了锐化的图像。 您可能需要更改核并观察图像上的效果。

使用 OpenCV 的过滤和模糊处理

OpenCV 还具有许多过滤和卷积函数。 这些过滤函数为cv2.filter2D()， cv2.boxFilter()， cv2.blur()， cv2.GaussianBlur()， cv2.medianBlur()， cv2.sepFilter2D()和cv2.BilateralFilter()。 在本节中，我们将详细探讨所有这些函数。

二维卷积过滤器

cv2.filter2D()函数与scipy.signal.convolve2d()函数一样，使核与图像卷积，从而对图像应用线性过滤器。 cv2.filter2D()函数的优点是我们可以将其应用于具有两个以上维的数据。 我们也可以将其应用于彩色图像。

此函数接受输入图像，输出图像的深度（-1 表示输入和输出具有相同的深度），以及用于卷积运算的核作为参数。 以下代码演示了此函数的用法：

import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.2.03.tiff', 1)
input = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
output = cv2.filter2D(input, -1, np.ones((15, 15), np.uint8)/225)
plt.subplot(121)
plt.imshow(input)
plt.title('Input')
plt.axis('off')
plt.subplot(122)
plt.imshow(output)
plt.title('Output')
plt.axis('off')
plt.show()

以下是输出：

图 7.6 –同一图像的过滤和模糊版本

注意：

您可以在以下 URL 上找到有关卷积的交互式教程

低通过滤器

如前所述，低通过滤器允许低频分量通过它们。 边缘和噪声通常是高频分量。 这些被过滤掉。 因此，低通过滤器非常适合消除噪声，模糊和平滑图像。

OpenCV 库提供了用于执行低通滤波的现成函数。 我们不必从头开始编写程序即可应用低通过滤器。 这些函数具有用其定义编写的核代码。 我们只需要将参数传递给函数，函数就会自动创建核并将其应用于映像。

cv2.boxFilter()函数接受输入源图像ddepth以及核大小作为参数，将核应用于输入图像，然后返回模糊图像作为输出。 最后一个参数是normalize，可以将其传递为True或False的布尔值。 这将决定输出是否被标准化。 如果通过True值进行归一化，则输出乘以1 / (行数 * 列数)，会创建归一化框式过滤器效果，如果值为False，则将输出乘以1，这将产生非标准化的框式过滤器效果。

下面的行向我们展示了标准化框式过滤器的示例：

output = cv2.boxFilter(input, -1, (3, 3), normalize=True)

下面的行向我们展示了一个非规范化框过滤器的示例：

output = cv2.boxFilter(input, -1, (3, 3), normalize=False)

cv2.blur()函数直接创建归一化框过滤器并将其应用于图像。 我们必须将源输入图像和核的大小作为参数传递。 我们不必指定是否要标准化输出。 默认情况下，这将产生标准化输出。 以下两行产生相同的输出：

output = cv2.blur(input, (3, 3))
output = cv2.boxFilter(input, -1, (3, 3), normalize=True)

OpenCV cv2.GaussianBlur()函数将高斯核应用于输入图像。 我们必须将输入源图像和核大小作为参数传递给此函数的调用。 第三个参数是 X 轴方向上的标准差。 我们为此传递了 0 作为参数。 此函数可以滤除图像中的所有高斯噪声。 以下是此代码示例：

output = cv2.GaussianBlur(input, (3, 3), 0)

OpenCV cv2.medianBlur()函数应用中值过滤器并返回模糊图像。 该过滤器对于具有椒盐味类型的噪点的图像非常有效。 我们需要传递源输入图像和一个定义方阵大小的数字作为调用此函数的参数，如下所示：

output = cv2.medianBlur(img, 3)

此函数计算核成员所有值的中位数。 核中心的值替换为中值的计算值。 这是滑动窗口类型的过滤器，其中核矩阵的窗口在图像的矩阵上滑动，并且图像中与核矩阵的中心重叠的像素通过卷积运算使用计算得到的值进行处理。 中位数。

cv2.sepFilter2D()函数将可分离的线性过滤器应用于图像。 以下是一个示例函数调用：

output = cv2.sepFilter2D(img, ddepth=-1, kernelX=1, kernelY=1, delta=1)

在前面的函数调用中，我们具有以下内容：

• ddepth：输出图像的深度（如果源图像和目标图像相同，则为-1）
• kernelX：用于过滤每行的系数
• kernelY：用于过滤各列的系数
• delta：添加到过滤结果中的常量值

作为本章的练习，您可能要在其中一个程序中使用cv2.BilateralFilter()函数来过滤图像。

总结

在本章中，我们了解了噪声和低通滤波技术以及如何将其用于平滑图像。 如果我们希望从图像中消除各种类型的噪点，我们在本章中学习的技术将非常有用。 在编写用于实际应用（例如，使用 USB 网络摄像头实时检测运动）的程序时，将使用这些技术来消除，平滑和模糊噪声。

在下一章中，我们将研究高通滤波技术以及如何使用 OpenCV 提供的实现各种数学形态学操作符的各种功能来检测边缘。

八、高通过滤器和特征检测

在上一章中，我们了解了核和低通过滤器及其应用。 我们了解并演示了如何在模糊，平滑和消噪图像中使用低通过滤器。

在本章中，我们将学习并演示高通过滤器的用法。 这包括它们在图像处理和计算机视觉中的应用。 首先，我们将探讨拉普拉斯过滤器，沙尔过滤器和 Sobel 高通过滤器。 然后，我们将学习 Canny 边缘检测算法。 我们还将演示圆和直线的霍夫变换。 我们将通过使用哈里斯算法检测角点检测来得出结论。

以下是我们将在本章中介绍的主题的列表：

• 探索高通过滤器
• 使用 Canny 边缘检测器
• 使用霍夫变换查找圆和直线
• 哈里斯角点检测

在遵循了本章之后，您将能够使用高通过滤器来检测输入图像中的特征，例如边缘，角点，直线和圆。

技术要求

可以在 GitHub 上找到本章的代码文件。

观看以下视频，以查看这个页面上的“有效代码”。

探索高通过滤器

高通过滤器的概念与低通过滤器完全相反。 高通过滤器允许信息的高频分量（例如信号和图像）通过它们。 这就是为什么将它们称为高通过滤器的原因。 在图像中，边缘是高频分量。 我们在高通过滤器中使用的核会增强图像中的强烈分量。 这就是为什么当我们对图像应用高通过滤器时，会在输出中得到边缘。

注意：

您可以通过这个页面了解更多有关高通过滤器的信息。 信号过滤器的另一种类型是带通过滤器，它可以使一个频率范围（或频带）内的信号通过。 这些过滤器使我们可以突出显示图像的边缘并通过同时使用模糊来减少噪点。 您可以在这个页面上阅读有关它们的更多信息。

OpenCV 有许多库函数，可实现高通过滤器。 我们将研究如何使用Laplacian()，Sobel()和Scharr()函数。

注意：

您可以通过参考以下网页来详细了解高通滤波的数学方面：

https://www.tutorialspoint.com/dip/Sobel_operator.htm

https://www.tutorialspoint.com/dip/Laplacian_Operator.htm

以下是所有高通滤波函数常用的参数列表及其含义：

• src：这是要在其中检测边缘的源图像的参数。
• ddepth：这是用于确定目标图像深度的参数。-1表示源图像和目标图像具有相同的深度。 OpenCV 提供的高通滤波函数支持源图像和目标图像深度的以下组合：

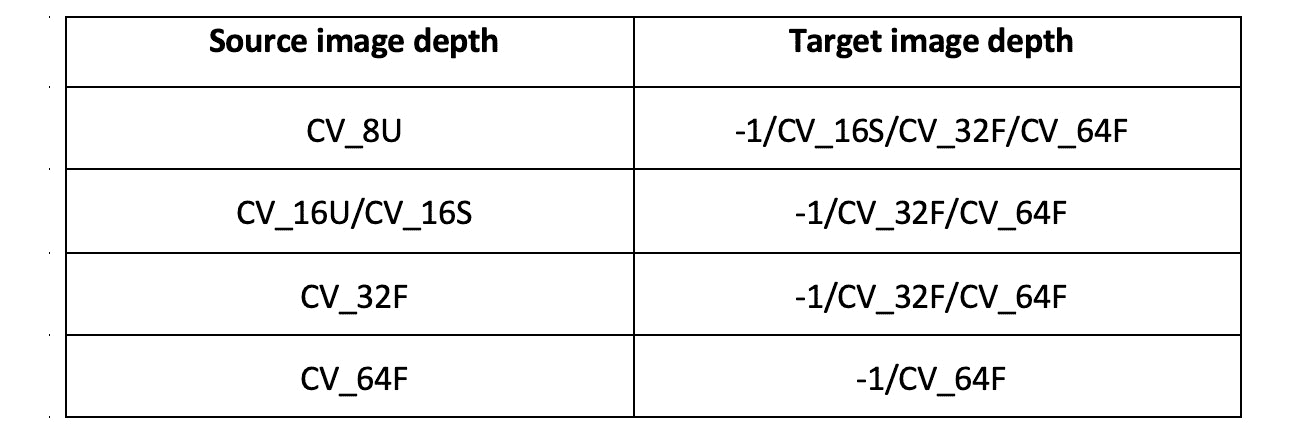
图 8.1 – OpenCV 支持的过滤器函数列表

• dx：这是X的导数的顺序（Laplacian()不需要）。
• dy：这是Y的导数的顺序（Laplacian()不需要）。
• ksize：这是核矩阵的大小（Sobel()函数或Laplacian()函数的正奇数，可以是1，3，5或7，Scharr()不需要）。
• scale：这是标度，是可选的。 这是计算的拉普拉斯算子值的可选比例的因素。 默认情况下不应用缩放。
• delta：这是增量的值。 这是一个可选常数，并添加到最终输出中。
• borderType：这是用于对位于边界处的像素进行像素外推的方法。

让我们编写一些代码来演示Sobel()，Laplacian()和Scarr()函数的功能。 在下面的代码中，我们使用Scarr()和Sobel()函数计算输入图像的X的拉普拉斯算式和一阶导数 ：

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.1.05.tiff', 0)
laplacian = cv2.Laplacian(img, ddepth=cv2.CV_32F, ksize=17,
                          scale=1, delta=0,
                          borderType=cv2.BORDER_DEFAULT)
sobel = cv2.Sobel(img, ddepth=cv2.CV_32F, dx=1, dy=0,
                  ksize=11, scale=1, delta=0,
                  borderType=cv2.BORDER_DEFAULT)
scharr = cv2.Scharr(img, ddepth=cv2.CV_32F, dx=1, dy=0,
                    scale=1, delta=0,
                    borderType=cv2.BORDER_DEFAULT)
images=[img, laplacian, sobel, scharr]
titles=['Original', 'Laplacian', 'Sobel', 'Scharr']
for i in range(4):
    plt.subplot(2, 2, i+1)s
    plt.imshow(images[i], cmap = 'gray')
    plt.title(titles[i])
    plt.axis('off')
plt.show()

具有Laplacian()，Scharr()和Sobel()函数的图像X的导数的计算[ 返回输入图像中的垂直边缘。 以下屏幕截图显示了上述代码的输出：

图 8.2 –使用高通过滤器的 x 导数

我们可以将两个按钮连接到上拉配置的7和11GPIO 引脚，并对它们进行编程以调整dx和dy。 以下是执行此操作的代码：

import RPi.GPIO as GPIO
import cv2
x = 0
y = 1
cap = cv2.VideoCapture(0)
GPIO.setmode(GPIO.BOARD)
GPIO.setwarnings(False)
button1 = 7
button2 = 11
GPIO.setup(button1, GPIO.IN, GPIO.PUD_UP)
GPIO.setup(button2, GPIO.IN, GPIO.PUD_UP)
while True:
    print(x, y)
    ret, frame = cap.read()
    button1_state = GPIO.input(button1)
    if button1_state == GPIO.LOW:
        x = 0
        y = 1
    button2_state = GPIO.input(button2)
    if button2_state == GPIO.LOW:
        x = 1
        y = 0

现在，让我们使用cv2.Scharr()函数来计算输出图像：

    output = cv2.Scharr(frame, ddepth=cv2.CV_32F,
                        dx=x, dy=y,
                        scale=1, delta=0,
                        borderType=cv2.BORDER_DEFAULT)
    cv2.imshow('Salt and pepper Noise App', output)
    if cv2.waitKey(1) == 27:
        break
cap.release()
cv2.destroyAllWindows()

运行前面的程序，并从连接到 Raspberry Pi 板上的 USB 网络摄像头观察实时视频源上的边缘检测。 我们还可以将X衍生物添加到同一实时视频供稿的Y衍生物（用 Scharr 计算）中，如下所示：

import cv2
cap = cv2.VideoCapture(0)
while True:
    ret, frame = cap.read()
    output1 = cv2.Scharr(frame, ddepth=cv2.CV_32F,
                        dx=0, dy=1,
                        scale=1, delta=0,
                        borderType=cv2.BORDER_DEFAULT)

前一个代码段计算Y轴的 Scharr 导数。 现在，让我们编写X轴的 Scharr 导数的代码，如下所示：

    output2 = cv2.Scharr(frame, ddepth=cv2.CV_32F,
                        dx=1, dy=0,
                        scale=1, delta=0,
                        borderType=cv2.BORDER_DEFAULT)
    cv2.imshow('Addition of Vertical and Horizontal',
               cv2.add(output1, output2))
    if cv2.waitKey(1) == 27:
        break
cap.release()
cv2.destroyAllWindows()

运行前面的程序，观察添加的X和YScharr 衍生物。 您可以使用 Sobel 衍生工具实现类似的程序。 所有这些过滤器都用于检测图像中的边缘。

在下一节中，我们将看到如何使用高通过滤器通过 Canny 边缘检测算法来检测图像中的边缘。

使用 Canny 边缘检测器

Canny 边缘检测算法由 John Canny 开发。 Canny 的算法大量使用高通过滤器的概念。 它具有多个步骤。

注意：

您可以在这个页面上了解有关 Canny 边缘检测算法的更多信息。

OpenCV 具有cv2.Canny()函数，提供了 Canny 算法。 以下是该算法的步骤：

1. 将具有5 x 5像素大小的高斯核应用于输入图像以消除任何噪声。

2. 然后，我们计算滤波图像强度的梯度。 我们可以在此步骤中使用 L1 或 L2 范数。

3. 然后，我们应用非最大抑制，并为可能的边缘集确定候选者。

4. 最后一步是磁滞的操作。 我们根据传递给图像的阈值最终确定边缘。

   注意：

   您可以在这个页面和这个页面上详细了解 L1 和 L2 规范以及非最大抑制。

以下是cv2.Canny()函数的参数列表：

• img：我们需要检测边缘的输入源图像。
• threshold1：阈值的下限。
• threshold2：阈值的上限。
• L2gradient：如果此值为True，则该函数使用 L2 范数来计算边集，这更精确，但计算量大。 如果为False，则使用 L1 范数来计算边集，这需要较少的计算，但准确率较低。

此函数计算并返回源输入图像中检测到的边缘集。 以下代码很好地演示了此概念：

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.1.05.tiff', 0)
edges1 = cv2.Canny(img, 50, 300, L2gradient=False)
edges2 = cv2.Canny(img, 100, 150, L2gradient=True)
images = [img, edges1, edges2]
titles = ['Original', 'L1 Gradient', 'L2 Gradient']
for i in range(3):
        plt.subplot(1, 3, i+1)
        plt.imshow(images[i], cmap = 'gray')
        plt.title(titles[i])
        plt.axis('off')
plt.show()

先前代码的输出如下：

图 8.3 – Canny 边缘检测的输出

通过实时计算边缘，我们可以使前面的程序更有趣，从而可以通过 OpenCV 的跟踪栏来调整阈值：

import cv2
cv2.namedWindow('Canny')
img = cv2.imread('/home/pi/book/dataset/4.1.05.tiff', 0)
def empty(z):
    pass
cv2.createTrackbar('Threshold 1', 'Canny', 50, 100, empty)
cv2.createTrackbar('Threshold 2', 'Canny', 150, 300, empty)
while(True):
    l1 = cv2.getTrackbarPos('Threshold 1', 'Canny')
    l2 = cv2.getTrackbarPos('Threshold 2', 'Canny')
    output = cv2.Canny(img, l1, l2, L2gradient=False)
    cv2.imshow('Canny', output)
    if cv2.waitKey(1) == 27:
        break
cv2.destroyAllWindows()

在前面的代码中，我们为 Canny 算法的上下阈值创建了两个跟踪条。 我们使用 L1 范数来计算边缘。 输出如下：

图 8.4 –带轨迹条的 Canny 边缘检测算法的输出

我们可以将此算法应用于实际图像，例如来自网络摄像头的实时视频。 在下一节中，我们将学习如何使用霍夫变换来检测圆和直线。

使用霍夫变换查找圆和直线

OpenCV 提供了cv2.HoughCircles()函数，用于使用霍夫方法检测图像中的圆。 这将返回检测到的圆的中心和半径。 它接受图像，（cv2.HOUGH_GRADIENT）检测方法，分辨率的反比，要检测的圆心之间的最小距离，内部使用的 Canny 方法的最高阈值 ，累加器的阈值以及要检测的圆的最大和最小距离。

注意：

您可以在这个页面上找到有关圆的霍夫变换的数学方面的更多详细信息。

在以下代码中，我们接受来自 USB 网络摄像头的实时视频提要作为输入。 然后，我们通过模糊输入帧消除噪声，然后将模糊帧传递给cv2.HoughCircles()函数的调用。 然后，我们使用cv2.Circle()函数可视化检测到的圆，如下所示：

import cv2
cap = cv2.VideoCapture(0)
while (True):
    ret , frame = cap.read()
    grey = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
    blur = cv2.blur(grey, (5, 5))
    circles = cv2.HoughCircles(blur,
                               method=cv2.HOUGH_GRADIENT,
                               dp=1, minDist=200,
                               param1=50, param2=13,
                               minRadius=30, maxRadius=175)
    if circles is not None:
        for i in circles [0,:]:
            cv2.circle(frame, (i[0], i[1]), i[2], (0, 255, 0), 2)
            cv2.circle(frame, (i[0], i[1]), 2, (0, 0, 255), 3)
    cv2.imshow('Detected', frame)
    if cv2.waitKey(1) == 27:
        break
cv2.destroyAllWindows()
cap.release()

运行前面的程序并观察输出。 它应如下所示：

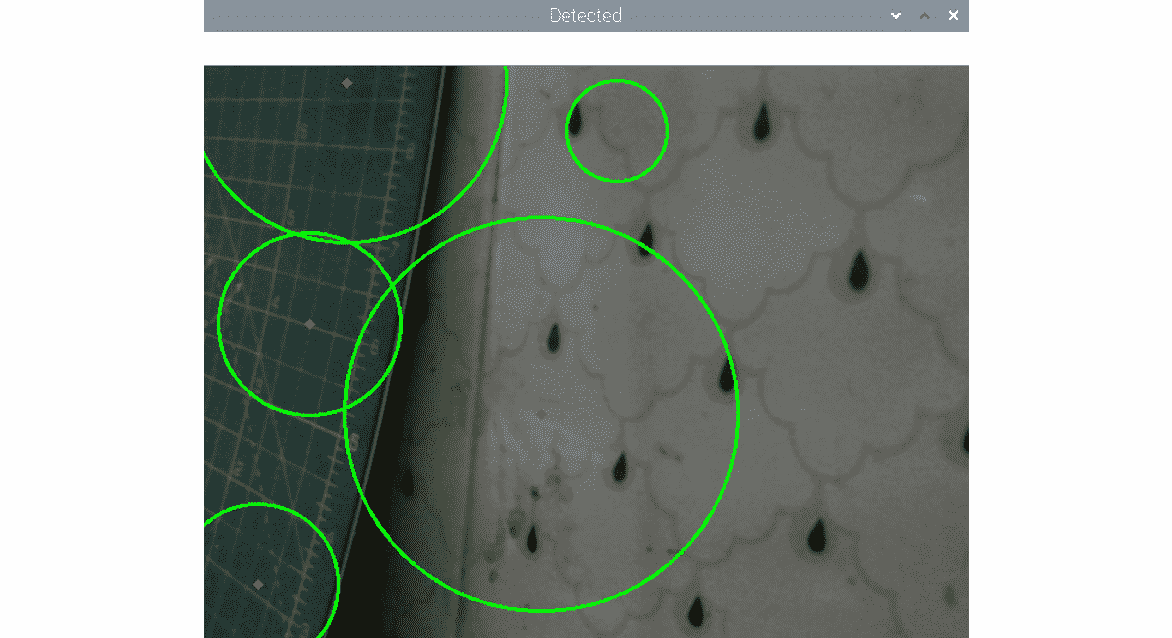
图 8.5 –检测到的圆圈

OpenCV cv2.HoughLines()函数检测图像中的线。 它接受灰度图像，ρ值（累加器的距离精度），θ（累加器的角度精度）和累加器阈值参数作为参数。 我们将通过实时 USB 网络摄像头视频提要进行演示。 返回的输出为极坐标格式，必须在可视化之前将其转换为X/Y坐标系：

import numpy as np
import cv2
cap = cv2.VideoCapture(0)
while True:
    ret, img = cap.read()
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    edges = cv2.Canny(gray, 50, 250, apertureSize=5,
                      L2gradient=True)
    lines = cv2.HoughLines(edges, 1, np.pi/180, 200)
    if lines is not None:
        for rho,theta in lines[0]:
            a = np.cos(theta)
            b = np.sin(theta)
            x0 = a*rho
            y0 = b*rho
            pts1 = (int(x0 + 1000*(-b)), int(y0 + 1000*(a)))
            pts2 = (int(x0 - 1000*(-b)), int(y0 - 1000*(a)))
            cv2.line(img, pts1, pts2, (0, 0, 255), 2)
    cv2.imshow('Detected Lines', img)
    if cv2.waitKey(1) == 27:
        break
cv2.destroyAllWindows()
cap.release()

运行前面的代码，然后观察其输出。 输出如下：

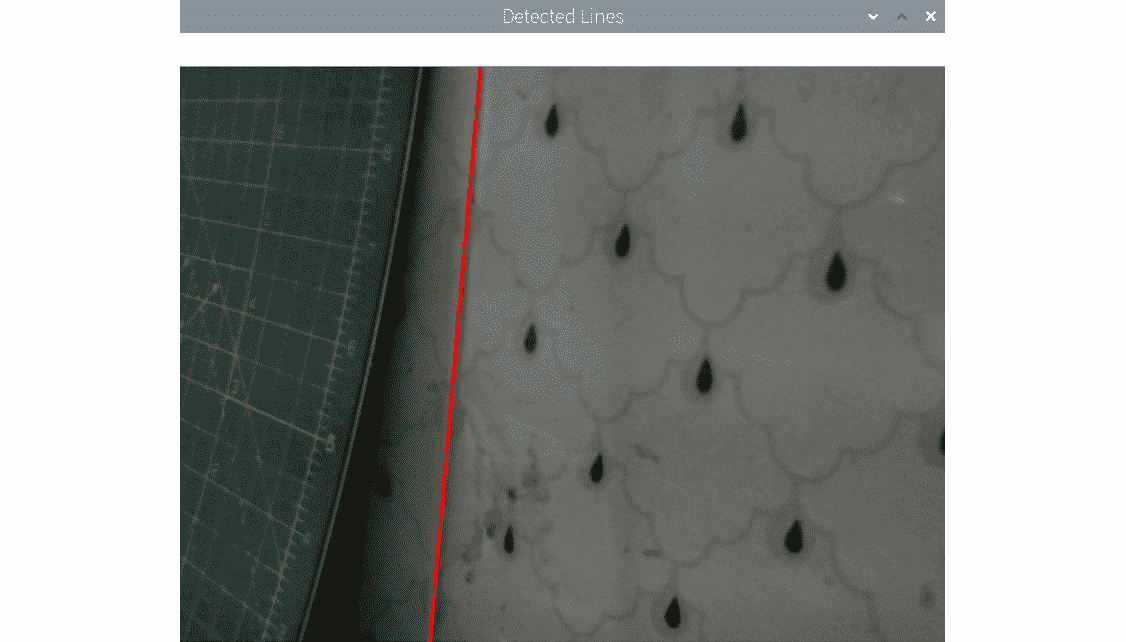
图 8.6 –检测到的线

对于给定的输入，必须对进行精细调整。 这意味着，如果在正确的位置看不到任何线或圆，则可以尝试调整传递给这些霍夫变换函数的参数的值。 有时，它可能会产生错误的结果，因为即使输入框中没有任何内容，也可以看到直线和圆圈。 同样，为了获得正确的结果，我们必须调整传递给这些函数的参数的值。

哈里斯角点检测

OpenCV 具有cv2.cornerHarris()函数，用于检测角。 其参数如下：

• img：输入图像，必须为灰度并且具有float32类型。
• blockSize：这是考虑进行角点检测的邻域的大小。
• ksize：使用的 Sobel 导数的光圈参数。
• k：等式中使用的自由哈里斯检测器参数。

以下是实现哈里斯角点检测的示例程序：

import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.1.05.tiff', 0)
img = np.float32(img)
dst = cv2.cornerHarris(img, 2, 3, 0.04)
ret, dst = cv2.threshold(dst, 0.01*dst.max(), 255, 0)
dst = np.uint8(dst)
plt.imshow(dst, cmap='gray')
plt.axis('off')
plt.show()

在前面的程序中，我们将图像转换为 32 位浮点格式，然后将其提供给角点检测函数。 然后，我们将图像阈值化。 我们使用0.01 * dst.max()作为阈值来计算二进制图像。 然后，我们将输出转换为 8 位整数格式，以便可以使用 Matplotlib 显示输出图像，如下所示：

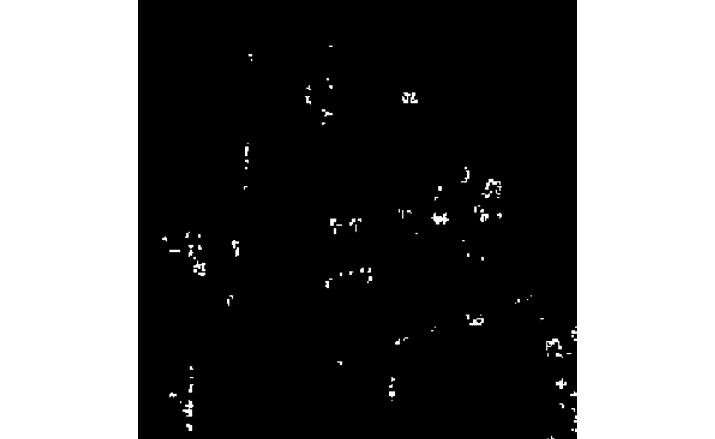
图 8.7 –检测到的角

我们可以在工业和机器人应用中使用这种角检测方法来检测规则和可预测对象的角。 它在现实世界的自动化中非常有用。

实践

要实践本章所学内容，请在 OpenCV 中探索HoughLinesP()，goodFeaturesToTrack()和FastFeatureDetector()函数以检测各种特征。 使用这些函数编写程序，以使用概率霍夫变换和其他特征检测行。

总结

在本章中，我们学习了高通过滤器的概念和演示。 我们对图像应用了高通过滤器，以获得各种结果。 我们还演示了各种检测特征的技术，例如角，线，边和圆。 所有这些特征检测算法都依赖于高通滤波。 Canny 的边缘检测算法使用高斯高通过滤器。 哈里斯角点检测算法使用 Sobel 空间导数。 所有这些几何特征检测算法通常在工业自动化，智能车辆和机器人技术的现实生活中使用。

在本书的下一章中，我们将学习概念并演示降级图像的恢复。 图像分割； 一维，二维和多维数据的 K 均值聚类； 使用 K 均值聚类的图像量化； 并详细估计深度图。

九、图像还原，分割和深度图

在上一章中，我们演示了如何在算法中使用高通过滤器及其应用来检测边缘。

在本章中，我们将学习一些有关图像的高级处理技术。 首先，我们将开始恢复损坏或降级的图像。 然后，我们将探讨各种类型的分割技术的基础。 我们已经看到阈值化是分割的基本形式。 我们将在本章中更详细地探讨这个概念。 最后，我们将计算视差图并估计图像中对象的深度。

在本章中，我们将介绍以下主题：

• 使用修复还原损坏的图像
• 分割图像
• 视差图和深度估计

到本章末，我们将能够还原损坏的图像，对图像应用各种分割算法，并使用视差图估计对象的深度。

技术要求

可以在 GitHub 上找到本章的代码文件。

观看下面的视频，以查看这个页面上的“有效代码”。

使用修复功能恢复损坏的图像

图像恢复是从图像的现有部分重建受损部分的计算过程。 如果我们用照相相机在胶片上拍摄图像并将其显影在纸上，则相纸会随着时间的流逝而退化，从而导致照片质量下降。 传感器故障以及相机镜头上的灰尘和污垢等瑕疵会在拍摄的图像中引入错误。 发送和接收的过程还会在数字图像中引入错误。 图像修复技术可以还原退化和损坏的图像。 许多算法可用于修复图像。 OpenCV 库使用cv2.inpaint()函数实现了两种修复方法。

此函数接受降级或损坏的源图像，图像修复的遮罩，修复邻域的大小以及修复方法作为参数。 修补遮罩是由灰度图像表示的损坏区域，其中白色像素是指要修复或修补的区域。 下面的代码演示了我们上面讨论的两种方法。 两种方法产生的输出几乎相同。 我们可以使用免费的图像编辑软件（例如 GIMP）来创建损坏的遮罩。 看下面的代码：

import cv2
import matplotlib.pyplot as plt
image = cv2.imread('/home/pi/book/dataset/Damaged.tiff')
mask = cv2.imread('/home/pi/book/dataset/Mask.tiff', 0)
input = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
output_TELEA = cv2.inpaint(input, mask, 5, cv2.INPAINT_TELEA)
output_NS = cv2.inpaint(input, mask, 5, cv2.INPAINT_NS)
plt.subplot(221)
plt.imshow(input)
plt.title('Damaged Image')
plt.axis('off')
plt.subplot(222)
plt.imshow(mask, cmap='gray'),
plt.title('Mask')
plt.axis('off')
plt.subplot(223),
plt.imshow(output_TELEA)
plt.title('Telea Method')
plt.axis('off')
plt.subplot(224)
plt.imshow(output_NS)
plt.title('Navier Stokes Method')
plt.axis('off')
plt.show()

在前面的代码中，我们使用了两种技术。cv2.INPAINT_TELEA标志基于论文《基于快速行进方法的图像修复技术》中描述的技术，该论文由 Alexandru 编写并于 2004 年出版。

cv2.INPAINT_NS标志基于《Navier-Stokes，流体动力学以及图像和视频修补》中描述的技术，该论文由 Bertalmio Marcelo， Andrea L. Bertozzi 和 Guillermo Sapiro 于 2001 年撰写和发布。

以下是输出：

图 9.1 –恢复降级的图像

在前面的输出中，第一张图像是损坏的图像。 第二个图像是对应于损坏的二进制掩码。 第二行中的图像是使用，Telea 方法和 Navier-Stokes 方法还原的图像。

注意

您可以在这个页面上找到有关图像修复的更多信息。

分割图像

图像的分割是将图像分为许多部分或部分（也称为段）的过程。 此过程使用特定条件执行。 我们可以将图像划分为段的最简单方法是通过阈值化。 我们已经在第 6 章，“颜色空间，变换和阈值”中了解并演示了阈值化技术。 在本章中，我们将演示另外两种分割方法。 这些方法是均值漂移算法和 K-Means 聚类。

均值漂移算法分割

Bogdan Georgescu 和 Chris M. Christoudias 开发了均值漂移算法，并用 C++ 实现。 相同算法的 Python 实现称为 PyMeanShift。 PyMeanShift 使用ndarray和 NumPy 来存储和处理图像。 这就是为什么它与基于 NumPy 的图像处理库（如 OpenCV，Mahotas 和 scikit-image）兼容的原因。

注意

您可以在项目 GitHub 页面上找到有关此内容的更多信息。

没有二进制包可以在 Linux，Unix 和其他基于它们的操作系统上安装 PyMeanShift。 我们必须构建它并从源代码安装它。 从以下 URL 下载最新版本的源代码。 下载将是一个 ZIP 文件。 将其复制到pi用户的主目录，/pi/home，然后提取它。 导航到我们将其解压缩到的目录，并在lxterminal上依次运行以下命令：

cd ~
cd pymeanshift-master/
sudo python3 setup.py build
sudo python3 setup.py install

安装完成后，在命令提示符上运行以下命令以检查安装是否成功：

python3 -c "import pymeanshift as pms"

pymeanshift库提供pms.segment()函数，该函数可分割由 NumPy ndarray表示的图像。 它接受要分割的源输入图像，空间半径，范围半径和最小密度作为参数。 然后，它返回一个分割的图像，一个标记的彩色图像和一组区域。 以下是用于演示功能的代码示例：

import cv2
import pymeanshift as pms
from matplotlib import pyplot as plt
img = cv2.imread('/home/pi/book/dataset/house.tiff', 1)
input = cv2.cvtColor(img, cv2.COLOR_BGR2RGB )
(segmented_image, labels_image, number_regions) = pms.segment(
    input, spatial_radius=2, range_radius=2, min_density=300)
plt.subplot(131)
plt.imshow(input)
plt.title('Input')
plt.axis('off')
plt.subplot(132)
plt.imshow(segmented_image)
plt.title('Segmented Output')
plt.axis('off')
plt.subplot(133)
plt.imshow(labels_image)
plt.title('Labeled Output')
plt.axis('off')
plt.show()

先前代码的输出如下：

图 9.2 –使用 PyMeanShift 进行分割

作为练习，将不同的参数值传递给函数参数并比较输出。 我们可以将其应用于来自网络摄像头的实时馈送视频，如下所示：

import cv2
import pymeanshift as pms
cap = cv2.VideoCapture(0)
while True:
    ret, frame = cap.read()
    (segmented_image, labels_image, number_regions) = pms.segment(
        frame, spatial_radius=2, range_radius=2, min_density=50)
    cv2.imshow('Segmented', segmented_image)
    if cv2.waitKey(1) == 27:
        break
cv2.destroyAllWindows()
cap.release()

通常，分段是在计算上非常昂贵的操作，因此，实时视频的每秒帧（FPS）非常低。 该的输出将类似于前一个（图 2）的输出。

K 均值聚类和图像量化

K 均值聚类算法是一种分类算法。 假设算法的输入是大小为n的集合，然后输出将该集合划分为k个分区数。 这就是为什么它被称为 K-Means 算法的原因。 本质上，基于特定标准，我们将数据划分或分类为k个类或分区。 将其应用于具有两个或多个维度的数据（即多维数据）时，称为聚类。 OpenCV 具有cv2.kmeans()函数，该函数实现了针对一维和多维数据的 K 均值聚类算法。 它接受以下参数的参数：

• Data：这是 K 均值聚类算法的输入数据。 此数据必须为浮点数字格式。

• K：算法输出中的分区总数。 必须事先知道（如果输入是彩色图像，这将意味着输出分割图像中的颜色数量）。

• Criteria：算法的终止条件。

• Attempts：使用不同的初始标签运行算法的次数。

• Flags：表示群集的初始中心的位置，这些群集以下列任何一个值作为参数传递：

  cv2.KMEANS_RANDOM_CENTERS 
  

  cv2.KMEANS_PP_CENTERS 
  

  cv2.KMEANS_USE_INITIAL_LABELS
  

让我们尝试首先演示用于一维数据的程序。 我们将为此创建自己的随机数据。 让我们创建和可视化数据：

import numpy as np
import cv2
from matplotlib import pyplot as plt
x = np.random.randint(25, 100, 25)
y = np.random.randint(175, 255, 25)
z = np.hstack((x, y))
z = z.reshape((50, 1))
z = np.float32(z)
plt.hist(z, 256, [0, 256])
plt.show()

样本随机数据将类似于以下输出：

图 9.3 –一维数据

我们可以清楚地看到数据分为两组。 现在，让 Raspberry Pi 对它进行分类，并突出显示组及其中心。 删除或注释掉前面代码的最后两行，并添加以下行：

criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
flags = cv2.KMEANS_RANDOM_CENTERS
compactness, labels, centers = cv2.kmeans(z, 2,
                                          None,
                                          criteria,
                                          10, flags)
A = z[labels==0]
B = z[labels==1]
plt.hist(A, 256, [0, 256], color = 'g')
plt.hist(B, 256, [0, 256], color = 'b')
plt.hist(centers, 32, [0, 256], color = 'r')
plt.show()

让我们运行前面的程序。 请注意，我们正在重新运行对np.random.randint()函数的调用，因此数据集将略有不同。 但是，它将具有两个不同的组，突出显示如下：

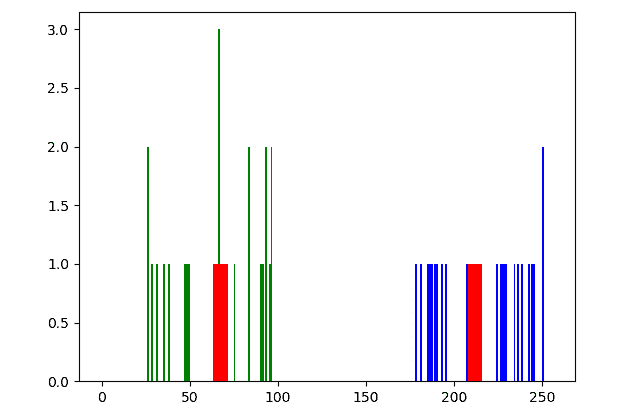
图 9.4 –适用于一维数据的 K-均值

我们可以在二维数据中实现此方法，如下所示：

import numpy as np
import cv2
from matplotlib import pyplot as plt
X = np.random.randint(25, 50, (25, 2))
Y = np.random.randint(60, 85, (25, 2))
Z = np.vstack((X, Y))
Z = np.float32(Z)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
ret,label,center=cv2.kmeans(Z, 2, None, criteria,
                            10, cv2.KMEANS_RANDOM_CENTERS)
A = Z[label.ravel()==0]
B = Z[label.ravel()==1]
plt.scatter(A[:,0], A[:,1])
plt.scatter(B[:,0], B[:,1], c = 'g')
plt.scatter(center[:,0], center[:,1],
            s = 80, c = 'r', marker = 's')
plt.xlabel('X - Axis')
plt.ylabel('Y - Axis')
plt.show()

输出如下：

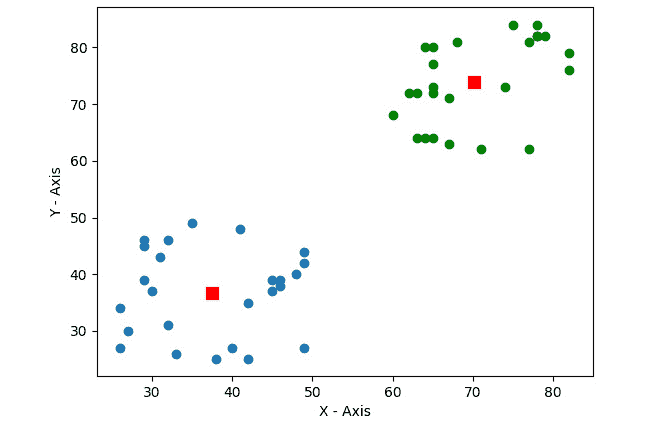
图 9.5 –二维数据的 K 均值

在前面的输出中，我们可以清楚地看到我们的数据分为两组。 让我们编写将 K-Means 聚类算法应用于彩色图像的代码，其中k的大小值为2，4和12：

import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('/home/pi/book/dataset/4.2.03.tiff', 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
Z = img.reshape((-1, 3))
Z = np.float32(Z)
criteria = (cv2.TERM_CRITERIA_EPS +
            cv2.TERM_CRITERIA_MAX_ITER,
            10, 1.0)

在前面的代码中，我们正在彩色模式下读取图像并对其进行重塑。 我们还将其转换为 32 位浮点格式。 然后，我们在最后一行设置聚类标准。

让我们以k的值计算为2的量化图像，如下所示：

k = 2
ret, label1, center1 = cv2.kmeans(Z, k, None, criteria, 10,
                                 cv2.KMEANS_RANDOM_CENTERS)
center1=np.uint8(center1)
res1 = center1[label1.flatten()]
output1 = res1.reshape((img.shape))

在前面的代码中，我们正在使用cv2.kmeans()函数计算群集，然后在将数据转换为 8 位整数格式后对其进行展平和整形。

现在，我们以k的值为4的方式计算量化图像：

k = 4
ret, label1, center1 = cv2.kmeans(Z, k, None, criteria, 10,
                                 cv2.KMEANS_RANDOM_CENTERS)
center1=np.uint8(center1)
res1 = center1[label1.flatten()]
output2 = res1.reshape((img.shape))

现在让我们以k的值作为12来计算量化的图像，如下所示：

k = 12
ret, label1, center1 = cv2.kmeans(Z, k, None, criteria, 10,
                                 cv2.KMEANS_RANDOM_CENTERS)
center1=np.uint8(center1)
res1 = center1[label1.flatten()]
output3 = res1.reshape((img.shape))

最后，让我们使用 Matplotlib 在网格中显示所有图像：

output = [img, output1, output2, output3]
titles = ['Original Image', 'K=2', 'K=4', 'K=12']
for i in range(4):
    plt.subplot(2, 2, i+1)
    plt.imshow(output[i])
    plt.title(titles[i])
    plt.xticks([])
    plt.yticks([])
plt.show()

首先，在前面的代码中，我们使用cv2.KMEANS_RANDOM_CENTERS标志为所有集群分配随机中心。 我们编写的程序的以下输出具有 2、4 和 12 种颜色的原始图像和使用量化的分割图像。 以下是输出：

图 9.6 – K 均值聚类和图像量化

作为练习，使用函数的自变量的不同值运行前面的程序，然后比较输出。 在网络摄像头的实时视频中实现此功能将很有趣。 不要期望高帧速率，因为它在计算上非常昂贵。

K 均值和均值漂移算法的比较

K 均值算法的时间复杂度为O(n)。 均值漂移分割算法的时间复杂度为O(n²)。 这种复杂性的差异是因为 K-Means 算法在运行时通过参数提供了群集数。 均值漂移分割算法必须在执行时自行计算群集数。 在我们不知道群集数的应用中，必须使用均值漂移算法。 但是，当我们已经知道群集的数目时，建议您使用 K-Means 算法，因为如果事先知道群集的数目，它的运行速度会大大提高。

视差图和深度估计

视差是指在由左眼和右眼或相机拍摄的图像中，对象位置的不同。 这种差异或视差是由视差引起的。 我们的大脑使用有关视差的信息来估计物体的深度（即它们与我们的距离）。 通过将此原理应用于网络摄像头捕获的图像对中的每个像素，我们可以计算两个图像之间的视差。 此视差信息可用于计算估计深度，从而模仿灵长类动物大脑的功能。

在生物学方面，这被称为，即立体视觉，这使我们能够从三个维度进行观察。 OpenCV 提供了cv2.StereoBM.compute()函数，该函数接受左图像和右图像作为参数，并返回该图像对的视差图。StereoBM_create()函数初始化立体状态。 它可以有许多差异和块大小作为参数。 默认情况下，它们分别是 0 和 21。 在下面的示例中，我们使用默认参数进行调用。 此立体状态用于通过cv2.StereoBM.compute()函数来计算视差图。 我们需要两个图像作为输入。 这些图像之一对应于右相机的输入，另一图像对应于左相机的输入。 以下代码使用这两个函数演示了此概念：

import cv2
import matplotlib.pyplot as plt
Right= cv2.imread('/home/pi/book/dataset/imRsmall.jpg', 0)
Left = cv2.imread('/home/pi/book/dataset/imLsmall.jpg', 0)
stereo_BM_state=cv2.StereoBM_create()
output_map=stereo_BM_state.compute(Left, Right)
titles=['Left', 'Right', 'Depth Map']
output=[Left, Right, output_map]
for i in range(3):
    plt.subplot(1, 3, i+1)
    plt.imshow(output[i], cmap='gray')
    plt.title(titles[i])
    plt.axis('off')
plt.show()

前面的代码的输出如下：

图 9.7 –从视差图估计深度

在前面的输出中，输出视差图中的较亮区域表示更多视差。 这意味着源输入图像中与视差输出图中的较亮区域相对应的对象更靠近相机。 类似地，视差输出图中的较暗颜色表示与源输入图像中那些区域相对应的对象距离相机更远。

总结

在本章中，我们了解了图像修复的概念以及受损和退化图像的恢复。 然后，我们展示了许多图像分割方法，包括均值漂移算法和 K 均值聚类。 最后，我们研究了如何使用视差图估计图像中对象的深度。 所有这些技术在许多现实应用中都是有用的。 例如，每当我们要通过网络发送图像时，我们都可以使用图像量化，从而减少带宽消耗。

在下一章中，我们将学习一些更高级的概念，例如直方图，灰度和彩色图像的直方图，图像轮廓的检测以及数学形态学操作。

十、直方图，轮廓和形态转换

在上一章中，我们了解并演示了围绕图像处理和计算机视觉领域的基本和中级概念。

从本章开始，我们将学习并演示高级概念，这些概念将使我们为编写现实生活中的应用做好准备。 首先，我们将研究使用ndarray计算直方图的理论基础。 然后，我们将学习如何针对灰度和彩色图像通道进行计算。 我们还将学习如何计算和可视化轮廓。 最后，我们将详细了解各种数学形态学操作，并演示如何将其与各种结构元素结合使用。 我们将学习并演示以下主题：

• 计算和可视化直方图
• 可视化图像轮廓
• 将形态学变换应用于图像

完成本章后，您将可以轻松地使用本文中讨论的所有概念。 在为计算机视觉领域的实际应用编写代码时，这些概念非常有用。

技术要求

可以在 GitHub 上找到本章的代码文件。

观看以下视频，以查看这个页面上的“正在执行的代码”。

计算和可视化直方图

直方图是数据分布的图形表示。 基本上，它是频率分布表的图形。 让我通过一个例子对此进行解释。 假设我们有一个数据集，例如(1, 2, 1, 3, 4, 1, 2, 3, 4, 4, 2, 3, 4)。 在这里，频率分布如下所示：

图 10.1 –频率分布

如果我们用绘制条形图，以便x轴表示元素，而y轴表示元素出现的频率，则被称为直方图。 我们可以使用np.histogram()来计算直方图。 plt.hist()可以计算并直接绘制它。 让我们编写一些代码，这些代码将使用这两个函数来解释上表中的数据：

import numpy as np
import matplotlib.pyplot as plt
a = np.array([1, 2, 1, 3, 4, 1, 2, 3, 4, 4, 2, 3, 4])
hist, bins = np.histogram(a)
print(hist)
print(bins)
plt.hist(a)
plt.show()

输出如下：

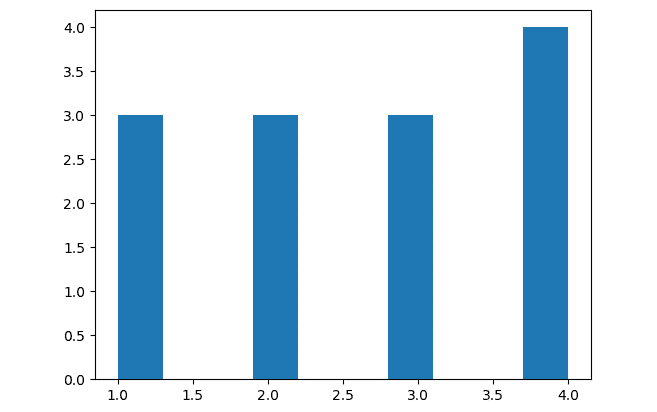
图 10.2 – ndarray的直方图

灰色阴影或颜色色调的出现的图形表示称为图像的直方图。 在图像的直方图中，我们在 X 轴上具有灰色阴影或颜色色调的值。 Y 轴代表，对于灰度图像，这些灰色阴影出现的次数，对于彩色图像，代表颜色的色调。

灰色或彩色图像的强度值在 X 轴上始终介于 0 到 255 之间。 Y 轴显示像素数。 对于灰度图像，将为完整图像计算直方图，而对于彩色图像，我们将分别计算颜色通道的直方图。

对于彩色图像，我们可以计算通道方向的直方图。 以下程序将灰度图像的直方图可视化：

import numpy as np
import matplotlib.pyplot as plt
import cv2
img = cv2.imread('/home/pi/book/dataset/boat.512.tiff', 0)
plt.subplots_adjust(hspace=0.25, wspace=0.25)
plt.subplot(1, 2, 1)
plt.imshow(img, cmap='gray')
plt.axis('off')
plt.title('Original Image')
plt.subplot(1, 2, 2)
hist, bins = np.histogram(img.ravel(),
                          bins=256,
                          range=(0, 255))
plt.bar(bins[:-1], hist)
plt.title('Histogram')
plt.show()

在前面的代码中，plt.subplots_adjust(hspace = 0.25, wspace = 0.25)函数调用调整了子图中的图像之间的水平和垂直空间。 我们正在使用np.histogram()来计算图像的直方图。 我们正在使用ravel()函数来使图像变平。

我们知道灰度的强度级别在 0 到 255 之间。因此，我们正在传递有关箱子和 range 的相关参数。 最后，我们使用plt.bar()使用条形图绘制直方图。 以下是输出：

图 10.3 –灰度图像的直方图

我们甚至可以使用plt.hist()函数来计算相同的直方图。 只需将包含np.histogram()和plt.bar()的行替换为以下行：

plt.hist(img.ravel(), bins=256, range=(0, 255))

输出如下：

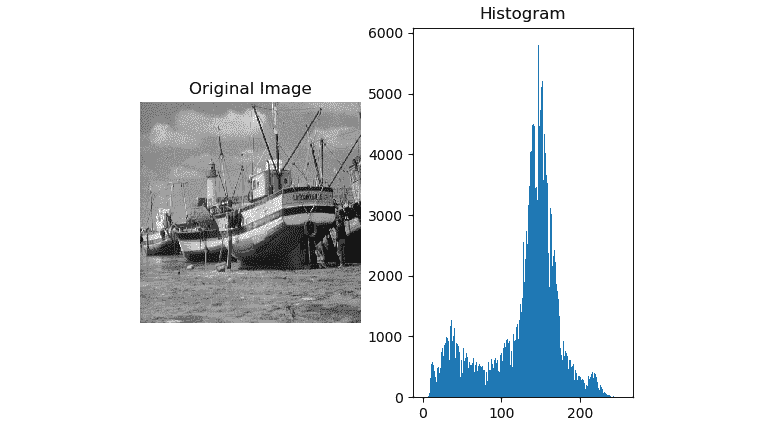
图 10.4 –灰度图像的直方图

正如我们所看到的，两种方法都产生相同的输出。 我们可以为彩色图像的所有通道计算直方图，并使用plt.hist()显示它们，如下所示：

import numpy as np
import matplotlib.pyplot as plt
import cv2
img = cv2.imread('/home/pi/book/dataset/house.tiff', 1)
b = img[:, :, 0]
g = img[:, :, 1]
r = img[:, :, 2]
plt.subplots_adjust(hspace=0.5, wspace=0.25)
plt.subplot(2, 2, 1)
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB),
           cmap='gray')
plt.axis('off')
plt.title('Original Image')
plt.subplot(2, 2, 2)
plt.hist(r.ravel(), bins=256, range=(0, 255), color='r')
plt.title('Red Histogram')
plt.subplot(2, 2, 3)
plt.hist(g.ravel(), bins=256, range=(0, 255), color='g')
plt.title('Green Histogram')
plt.subplot(2, 2, 4)
plt.hist(b.ravel(), bins=256, range=(0, 255), color='b')
plt.title('Blue Histogram')
plt.show() 

输出为，如下所示：

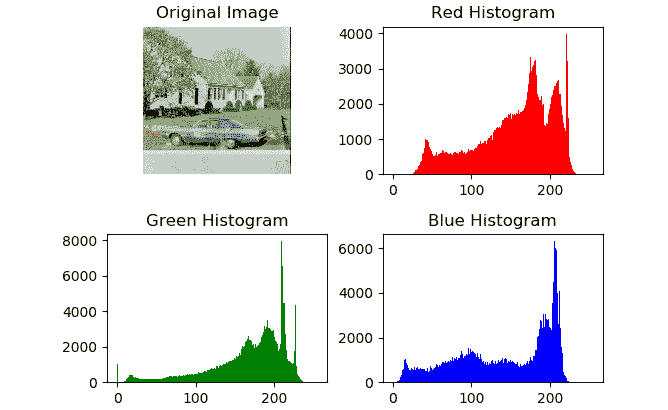
图 10.5 –彩色图像的直方图

OpenCV 提供cv2.calcHist()函数，以分别计算和可视化彩色图像的直方图通道。 cv2.calcHist()函数接受图像数组，掩码，通道索引，范围和大小作为参数，以为彩色图像的单个通道计算直方图。 以下示例通过分别计算和可视化每个颜色通道的直方图来演示：

import cv2
from matplotlib import pyplot as plt
img = cv2.imread('/home/pi/book/dataset/house.tiff', 1)
input=cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
histr_RED = cv2.calcHist([input], [0], None, [256], [0, 255])
histr_GREEN = cv2.calcHist([input], [1], None, [256], [0, 255])
histr_BLUE = cv2.calcHist([input], [2], None, [256], [0, 255])

前面的代码为输入彩色图像的所有组成通道计算直方图。 现在，让我们用 Matplotlib 显示直方图，如下所示：

plt.subplot(221)
plt.imshow(input)
plt.title('Original Image')
plt.axis('off')
plt.subplot(222)
plt.plot(histr_RED, color='r'),
plt.title('Red')
plt.xlim([0, 255])
plt.yticks([])
plt.subplot(223)
plt.plot(histr_GREEN, color='g')
plt.title('Green')
plt.xlim([0, 255])
plt.yticks([])
plt.subplot(224)
plt.plot(histr_BLUE, color='b')
plt.title('Blue')
plt.xlim([0, 255])
plt.yticks([])
plt.show()

前面的代码产生以下输出。 首先，它显示原始图像，然后将所有颜色通道的直方图可视化：

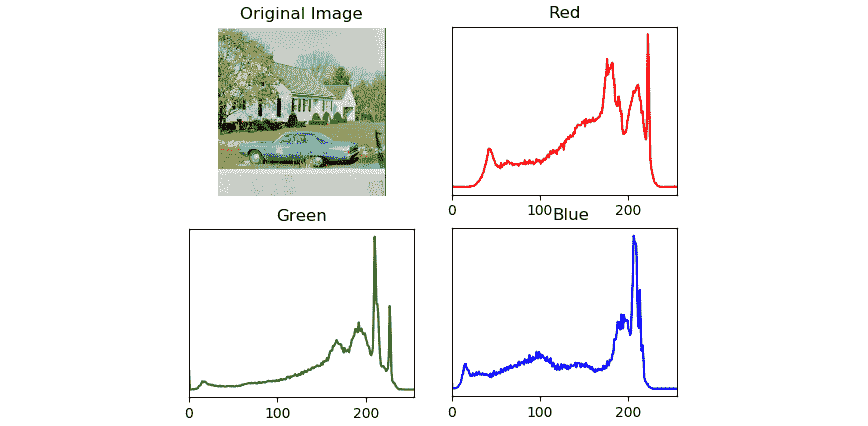
图 10.6 –彩色图像的直方图

在下一部分中，我们将学习并演示直方图均衡化。

直方图均衡

直方图均衡化是一种图像处理技术。 它用于改善图像的对比度。 它将散布到最频繁的强度值中。 这意味着图像的强度范围被拉长了。 此操作增加了较低对比度区域的对比度，从而增强了图像。 均衡直方图的方法有多种。 一种选择是，我们可以使用cv2.equalizeHist()函数来全局均衡图像的直方图。 我们可以使用的另一种方法称为对比度受限的自适应直方图均衡。 与整体直方图均衡化不同，它为图像的不同区域计算多个直方图。 这也称为局部直方图均衡：

1. 在下面的代码中，我们演示了如何均衡 RGB 图像各个通道的直方图，然后再次合并它们以获得对比度增强的输出彩色图像：

   import cv2
   

   import matplotlib.pyplot as plt
   

   img = cv2.imread('/home/pi/book/dataset/4.2.03.tiff', 1)
   

   img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
   

   R, G, B = cv2.split(img)
   

2. 让我们分别均衡图像的色彩通道，然后合并均衡通道以创建均衡图像：

   output1_R = cv2.equalizeHist(R)
   

   output1_G = cv2.equalizeHist(G)
   

   output1_B = cv2.equalizeHist(B)
   

   output1 = cv2.merge((output1_R,
   

   output1_G, output1_B))
   

3. 现在，让我们使用 CLAHE 方法来均衡颜色通道，然后将它们合并以获得带有 CLAHE 的均衡图像：

   clahe = cv2.createCLAHE(clipLimit=2.0,
   

   tileGridSize=(8, 8))
   

   output2_R = clahe.apply(R)
   

   output2_G = clahe.apply(G)
   

   output2_B = clahe.apply(B)
   

   output2 = cv2.merge((output2_R, output2_G,
   

   output2_B))
   

   output = [img, output1, output2]
   

   titles = ['Original Image',
   

   'Adjusted Histogram', 'CLAHE']
   

   for i in range(3):
   

   plt.subplot(1, 3, i+1)
   

   plt.imshow(output[i])
   

   plt.title(titles[i])
   

   plt.axis('off')
   

   plt.show()
   

   两种方法的输出如下。 第一个是原始图像，第二个是直方图调整后的图像，第三个图像是使用 CLAHE 生成的直方图均衡图像：

图 10.7 –直方图均衡

在下一节中，我们将学习并演示如何可视化图像轮廓。

可视化图像轮廓

将沿边界连续分布的所有点的曲线与像素的颜色具有相同值的曲线称为轮廓。 等高线用于检测图像中的边界。 轮廓线也用于图像分割。 通常使用图像中的边缘来计算轮廓。 但是，轮廓是闭合曲线，这是它们与图像边缘的主要区别。 在从图像中提取轮廓之前，对图像应用阈值运算始终是一个好主意。 它将提高轮廓运算的计算精度。

cv2.findContours()函数用于计算图像中的轮廓。 该函数接受图像数组，轮廓检索模式以及将轮廓逼近作为参数的方法。 然后，它返回图像中计算机轮廓的列表。 轮廓检索模式可以是以下任意一种：

• CV_RETR_CCOMP
• CV_RETR_TREE
• CV_RETR_EXTERNAL
• CV_RETR_LIST

轮廓近似的方法可以是以下任意一种：

• CV_CHAIN_APPROX_TC89_L1
• CV_CHAIN_APPROX_TC89_KCOS
• CV_CHAIN_APPROX_NONE
• CV_CHAIN_APPROX_SIMPLE

一旦使用cv2.findContours()函数计算了所有轮廓，就可以使用cv2.drawContours()函数将其轮廓化。 在第 4 章，“计算机视觉入门”中，我们已经学习并演示了可用于绘制线，圆和其他几何形状的函数。 cv2.drawContours()函数的工作方式相同。 此函数接受要显示轮廓的图像数组，使用cv2.findContours()函数检测到的轮廓列表，绘制轮廓的索引（我们必须通过-1作为该参数的自变量，以绘制图像中的所有轮廓），轮廓的颜色和厚度作为自变量。 以下程序计算并可视化图像中的所有轮廓：

import cv2
import matplotlib.pyplot as plt
img = cv2.imread('/home/pi/book/dataset/4.2.07.tiff', 1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray, 75, 255, 0)
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_TREE,
                                      cv2.CHAIN_APPROX_SIMPLE)
cv2.drawContours(img, contours, -1, (0, 0, 255), 2)
original = cv2.imread('/home/pi/book/dataset/4.2.07.tiff', 1)
original = cv2.cvtColor(original, cv2.COLOR_BGR2RGB)
output = [original, img]
titles = ['Original', 'Contours']
for i in range(2):
    plt.subplot(1, 2, i+1)
    plt.imshow(output[i])
    plt.title(titles[i])
    plt.axis('off')
plt.show()

输出如下：

图 10.8 –彩色图像中的轮廓

为了进一步探索轮廓的概念并更好地理解轮廓，请编写一些程序，它们使用cv2.findContours()和cv2.drawContours()函数，以及方法，颜色和模式的不同组合。 然后，将所有输出图像相互比较。

对图像执行形态转换

形态运算本质上是数学运算，它们会改变图像的形状。 这些操作最好用二进制图像直观地演示。 我们可以应用形态学操作来消除图像中的许多不必要的信息，例如噪声。 形态学操作接受图像和核作为输入。 我们将创建一个自定义的二进制图像作为二进制图像，因为这是视觉上展示形态学操作的最合适方法。

侵蚀的数学形态运算会收缩图像中的边界。 在二进制图像中，白色部分被视为前景，而黑色部分被视为背景。 腐蚀操作将所有像素设置在背景部分的边界上，从白到黑，从而有效缩小了白色区域。 形态膨胀与​​腐蚀操作正好相反。 它在前景边界附近添加了白色像素，因此可以有效地扩展图像中的白色前景。 任何形态学操作的强度取决于该运算中使用的核的类型和大小以及对该图像执行该运算的次数。 形态梯度操作是膨胀操作和腐蚀操作之间的计算差。

让我们看一下实际中的一些形态运算。 现在，让我们导入所有必需的库：

import numpy as np
import cv2
from matplotlib import pyplot as plt
Let us create a sample image,img = np.array([[0, 0, 0, 0, 0, 0, 0],
                [0, 0, 0, 0, 0, 0, 0],
                [0, 0, 255, 255, 255, 0, 0],
                [0, 0, 255, 255, 255, 0, 0],
                [0, 0, 255, 255, 255, 0, 0],
                [0, 0, 0, 0, 0, 0, 0],
                [0, 0, 0, 0, 0, 0, 0]], dtype=np.uint8)

让我们创建核并计算形态运算：

kernel = np.ones((3, 3), np.uint8)
erosion = cv2.erode(img, kernel, iterations = 1)
dilation = cv2.dilate(img, kernel, iterations = 1)
gradient = cv2.morphologyEx(img,
                            cv2.MORPH_GRADIENT,
                            kernel)
titles=['Original', 'Erosion',
        'Dilation', 'Gradient']
output=[img, erosion, dilation, gradient]

最后，让我们可视化计算的输出：

for i in range(4):
    plt.subplot(2, 2, i+1)
    plt.imshow(output[i], cmap='gray')
    plt.title(titles[i])
    plt.axis('off')
plt.show()

先前代码的输出如下：

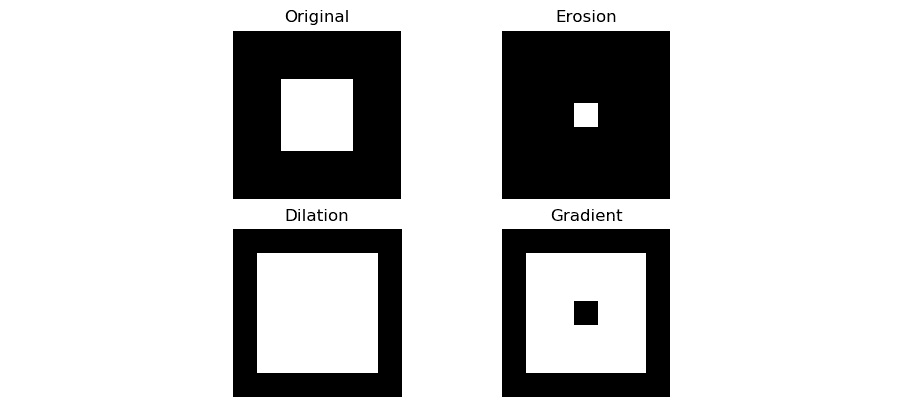
图 10.9 –形态运算

在前面的示例中，我们首先创建了一个自定义图像作为源或输入。 然后，我们创建了一个大小为3x3的核，并将其应用于源图像以进行所有数学形态学操作。 OpenCV 提供cv2.getStructuringElement()函数，该函数在参数中返回给定形状和大小的自定义核。 形状可以是cv2.MORPH_CROSS，cv2.MORPH_RECT或cv2.MORPH_ELLIPSE中的值之一。 另外，传递的大小必须是奇数正整数。 您可能需要打印并查看用于表示图像的矩阵中的值，以便了解数字的确切含义。 现在，让我们看一下各种结构元素：

1. 以交互方式打开 Python 3 并运行以下语句：

   >>> import cv2	
   

   >>> k = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
   

   >>> k
   

   输出如下：

   array([[1, 1, 1, 1, 1],
   

   [1, 1, 1, 1, 1],
   

   [1, 1, 1, 1, 1],
   

   [1, 1, 1, 1, 1],
   

   [1, 1, 1, 1, 1]], dtype=uint8)
   

2. 让我们看一个椭圆的结构元素：

   >>> k = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(5, 5))
   

   >>> k
   

   输出如下：

   array([[0, 0, 1, 0, 0],
   

   [1, 1, 1, 1, 1],
   

   [1, 1, 1, 1, 1],
   

   [1, 1, 1, 1, 1],
   

   [0, 0, 1, 0, 0]], dtype=uint8)
   

3. 让我们看一个跨结构元素：

   >>> k = cv2.getStructuringElement(cv2.MORPH_CROSS,(5, 5))
   

   >>> k
   

   输出如下：

   array([[0, 0, 1, 0, 0],
   

          [0, 0, 1, 0, 0],
   

          [1, 1, 1, 1, 1],
   

          [0, 0, 1, 0, 0],
   

          [0, 0, 1, 0, 0]], dtype=uint8)
   

   让我们通过使用自定义3x3交叉核查看其余的形态学操作。

4. 让我们导入所有必需的库：

   import numpy as np
   

   import cv2
   

   from matplotlib import pyplot as plt
   

5. 以下几行创建一个示例二进制图像：

   img = np.array([[0, 0, 0, 0, 0, 0, 0],
   

   [0, 0, 0, 0, 0, 0, 0],
   

   [0, 0, 255, 255, 255, 0, 0],
   

   [0, 0, 255, 255, 255, 0, 0],
   

   [0, 0, 255, 255, 255, 0, 0],
   

   [0, 0, 0, 0, 0, 0, 0],
   

   [0, 0, 0, 0, 0, 0, 0]], dtype=np.uint8)
   

6. 现在让我们为结构元素创建矩阵：

   kernel = cv2.getStructuringElement(cv2.MORPH_CROSS, (3, 3))
   

7. 现在，我们将数学形态学操作应用于样本二进制图像：

   open = cv2.morphologyEx(img,
   

   cv2.MORPH_OPEN,
   

   kernel)
   

   close = cv2.morphologyEx(img,
   

   cv2.MORPH_CLOSE,
   

   kernel)
   

   tophat = cv2.morphologyEx(img,
   

   cv2.MORPH_TOPHAT,
   

   kernel)
   

   blackhat = cv2.morphologyEx(img,
   

   cv2.MORPH_BLACKHAT,
   

   kernel)
   

   [

   hitmiss = cv2.morphologyEx(img,
   

   cv2.MORPH_HITMISS,
   

   kernel)
   

8. 现在让我们可视化输入和输出：

   titles=['Original', 'Open',
   

   'Close', 'Top hat',
   

   'Black hat', 'Hit Miss']
   

   output=[img, open, close,
   

   tophat, blackhat,
   

   hitmiss]
   

   for i in range(6):
   

   plt.subplot(2, 3, i+1)
   

   plt.imshow(output[i], cmap='gray')
   

   plt.title(titles[i])
   

   plt.axis('off')
   

   plt.show()
   

   前面的代码的输出如下：

图 10.10 –更多形态学操作

让我们了解在此演示的操作的含义。 腐蚀后接着膨胀被称为开口。 扩张然后腐蚀被称为开放。 高顶礼帽从图像中提取小元素和细节。 高礼帽是输入图像和图像开头之间的差异。 黑帽是图像关闭与图像本身之间的区别。 最终，命中或丢失是一种检测二进制图像中给定配置或模式的操作。

总结

在本章中，我们通常学习并演示了直方图的概念，并了解了如何从简单的一维数组创建简单的直方图。 然后，我们看到了如何可视化灰度和彩色图像的直方图。 我们还演示了如何使用图像轮廓。 最后，我们直观地演示了在数学形态学领域中执行的操作。 这些形态学操作对于现实生活中的应用将非常有用，我们将在第 11 章，“计算机视觉的现实应用*”中进行演示。

在下一章中，我们将通过构建真实的应用来演示在本章和前几章中学到的许多概念，例如运动检测器，带有绿屏的色度键以及静态图像中的条形码检测。 这将是激动人心且有趣的一章，它将总结我们迄今为止获得的所有知识。

标签：10,树莓,plt,img,编程,cv2,图像,np,import
From： https://www.cnblogs.com/apachecn/p/17332609.html