漫画：什么是希尔排序算法？

标签：插入排序 希尔 分组 增量 漫画 一尘 排序 复杂度

希尔排序（ShellSort）是以它的发明者Donald Shell名字命名的，希尔排序是插入排序的改进版，实现简单，对于中等规模数据的性能表现还不错

一、排序思想

前情回顾：漫画：什么是插入排序算法？（对插入排序不熟悉的强烈建议先阅读此文）

一天，一尘拿着扑克自己在那玩，刚被师傅看见了

数据有序程度越高，越高效（移动少）

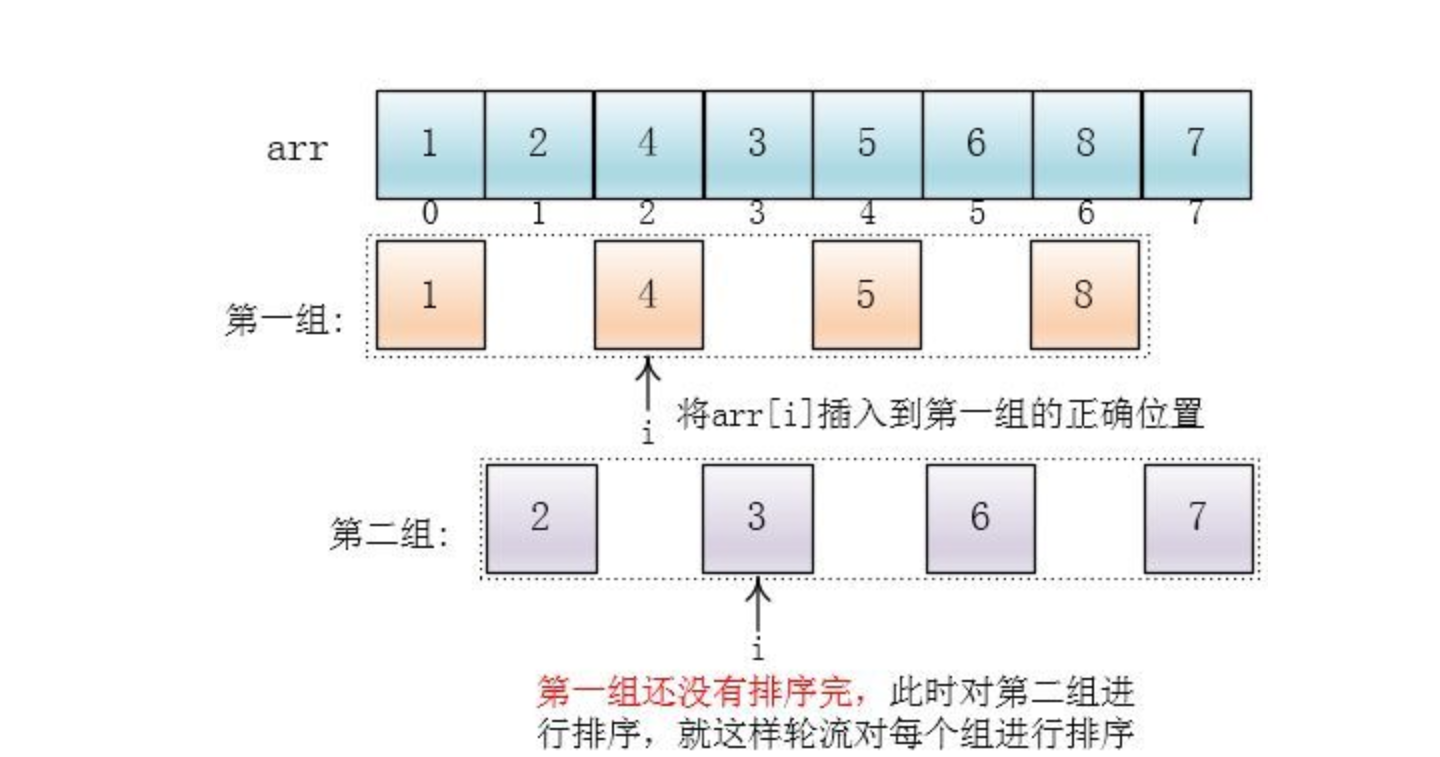
首先它把较大的数据集合分割成若干个小组（逻辑上分组），然后对每一个小组分别进行插入排序，此时，插入排序所作用的数据量比较小（每一个小组），插入的效率比较高

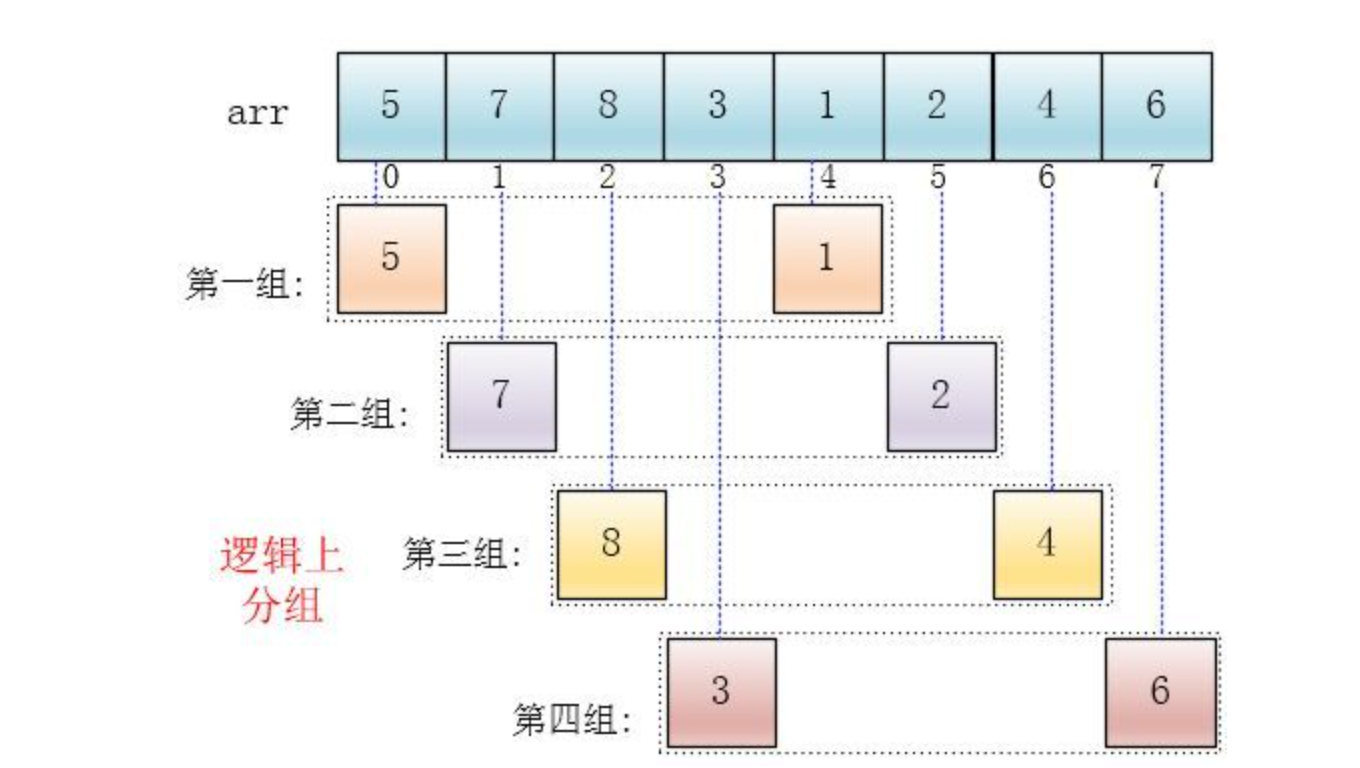
注意：下面有颜色的是逻辑上的分组，并没有实际地进行分组操作，在数组中的位置还是原来的样子，只是将他们看成这么几个分组（逻辑上分组）

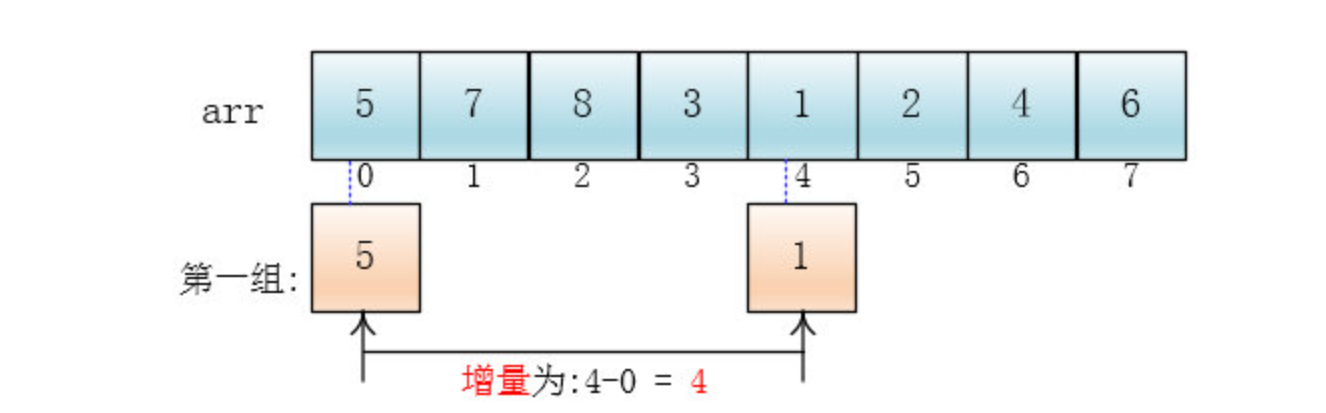
可以看出，他是按下标相隔距离为4分的组，也就是说把下标相差4的分到一组，比如这个例子中a[0]与a[4]是一组、a[1]与a[5]是一组...，这里的差值（距离）被称为增量

每个分组进行插入排序后，各个分组就变成了有序的了（整体不一定有序）

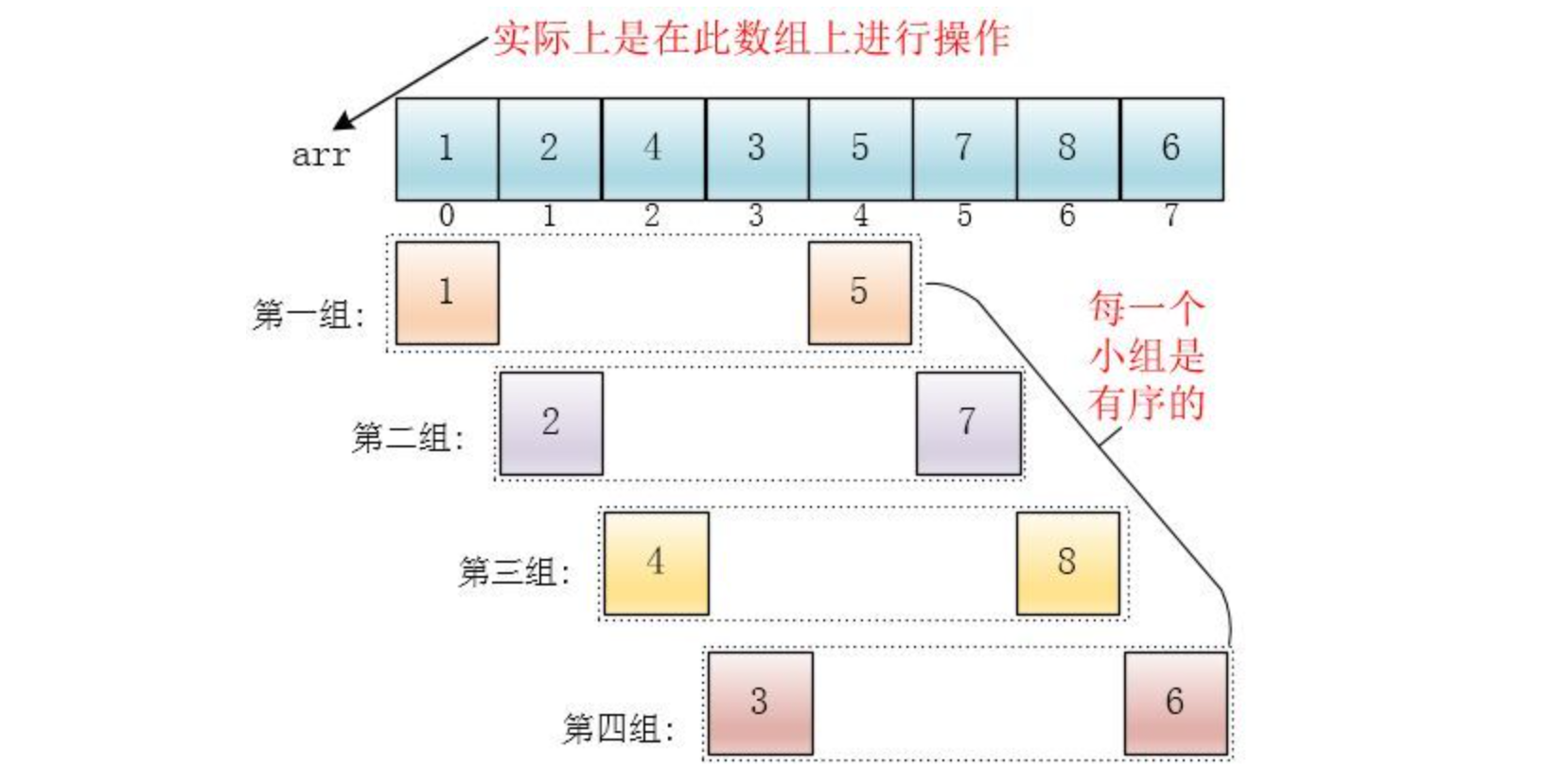
此时，整个数组变的部分有序了（有序程度可能不是很高）

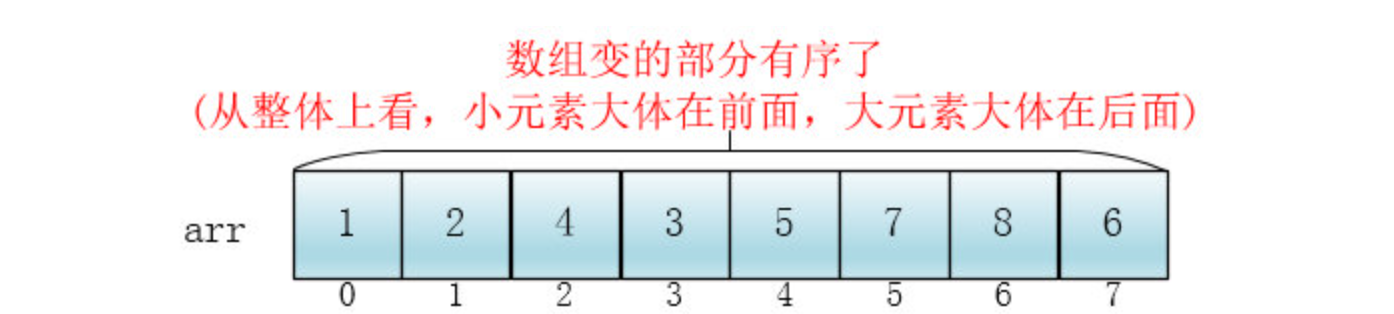
然后缩小增量为上个增量的一半:2，继续划分分组，此时，每个分组元素个数多了，但是，数组变的部分有序了，插入排序效率同样比较高

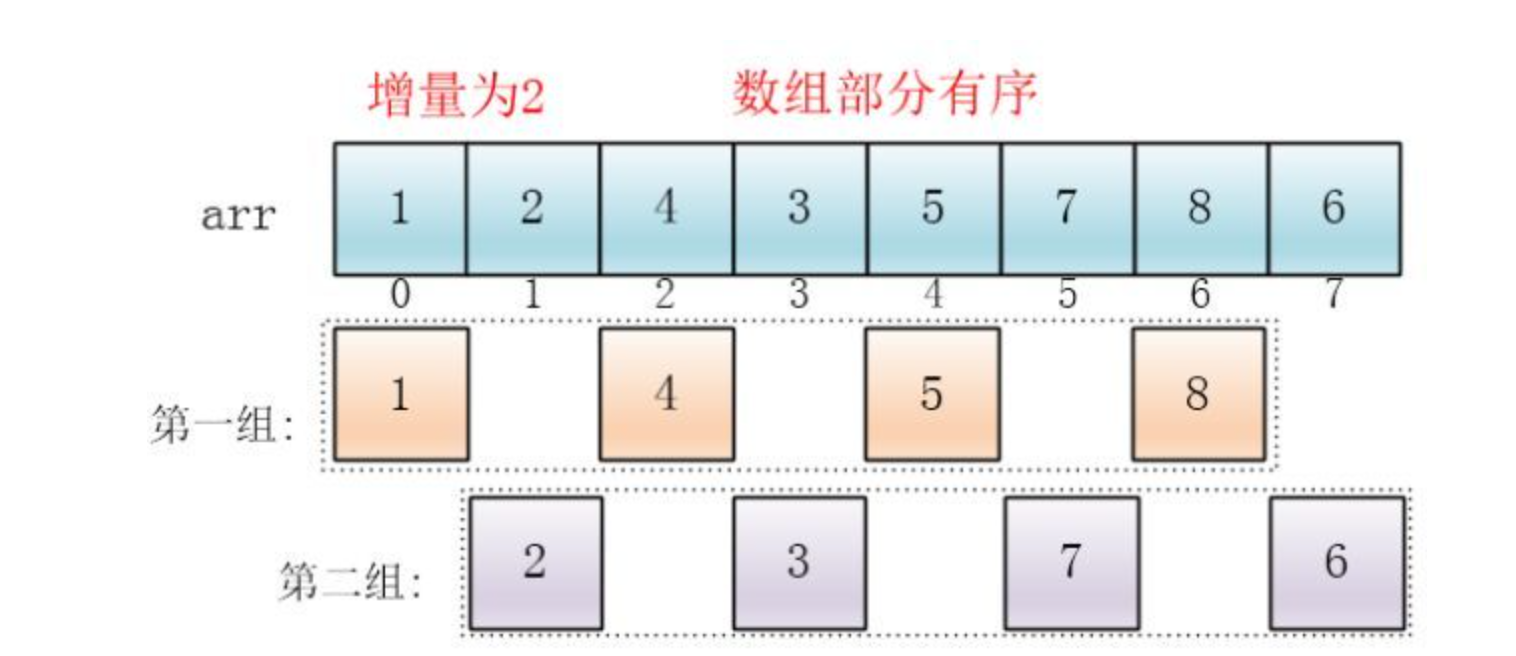
同理对每个分组进行排序（插入排序），使其每个分组各自有序

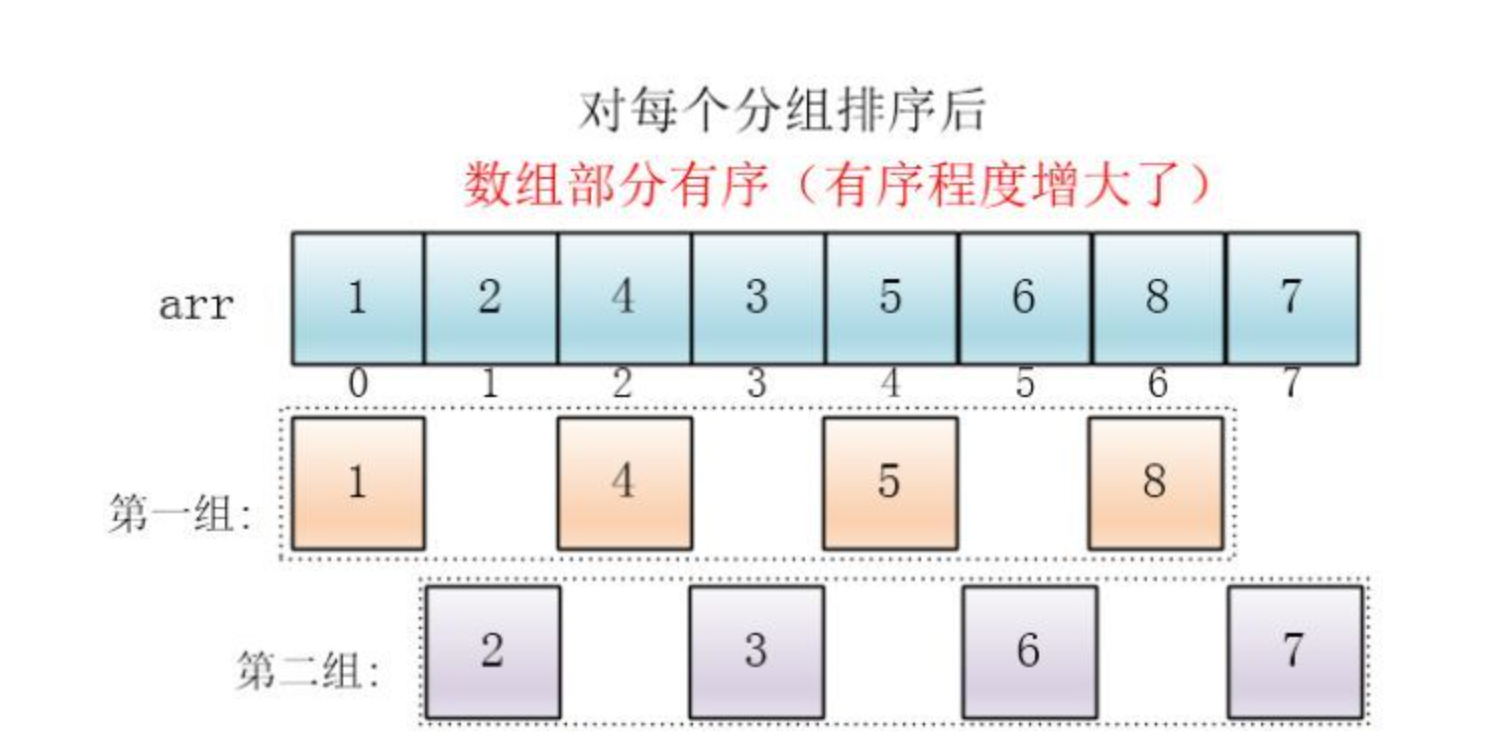
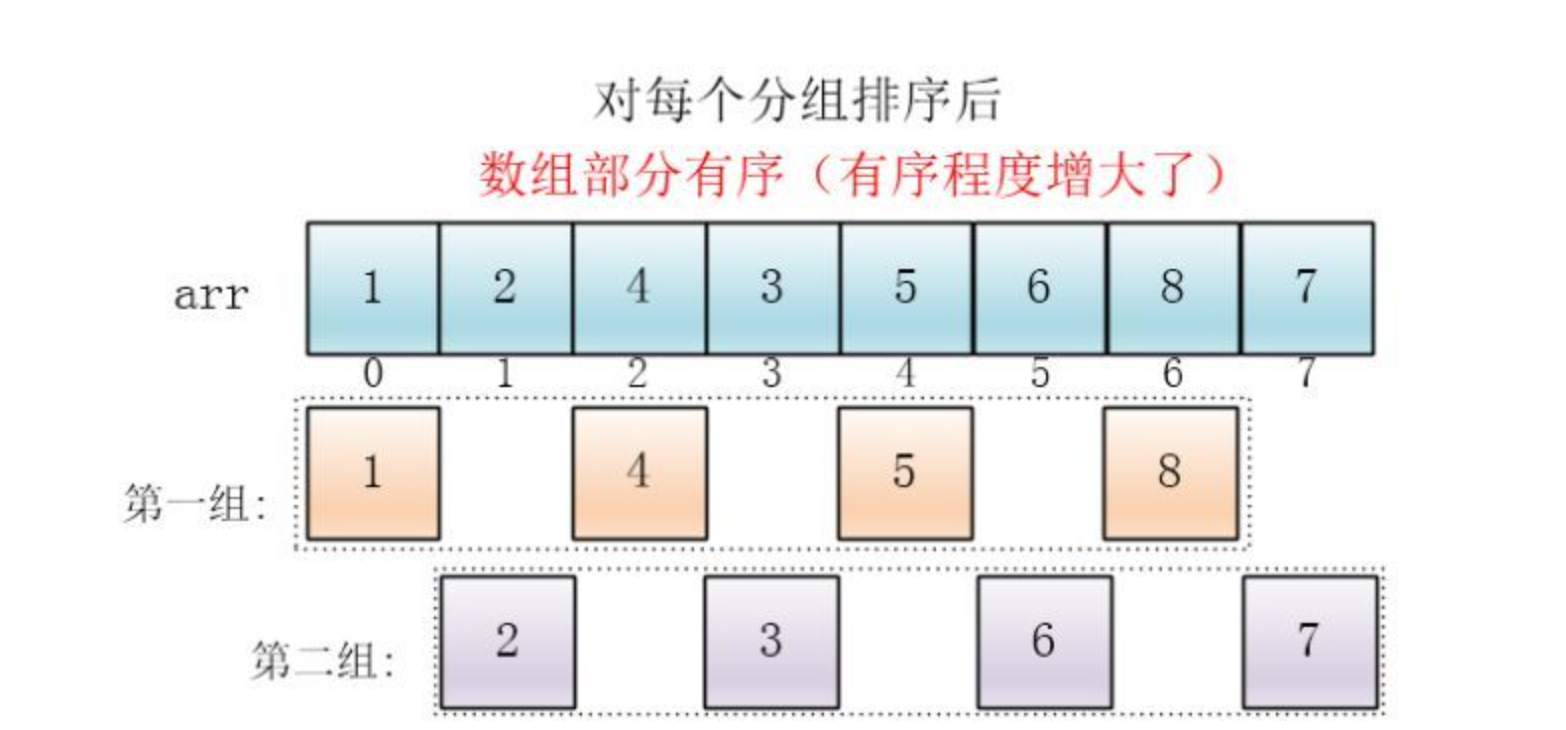
最后设置增量为上一个增量的一半：1，则整个数组被分为一组，此时，整个数组已经接近有序了，插入排序效率高

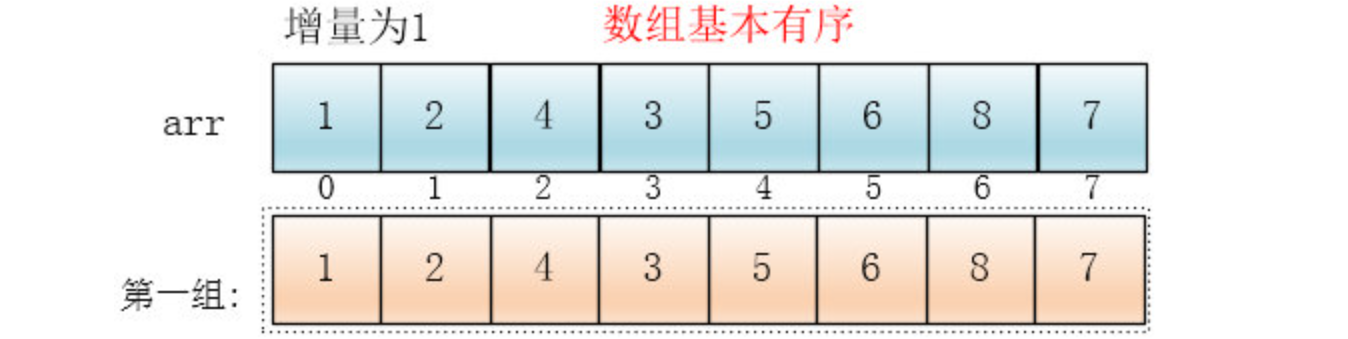
同理，对这仅有的一组数据进行排序，排序完成

二、排序代码

对于已经熟悉插入排序的一尘来说这并不是什么难事，很快，一尘写出了希尔排序的代码

随后一尘写出了插入arr[i]到所在组正确位置的代码（insertI）

insertI 和直接插入排序里的插入代码几乎完全一样

三、时间复杂度

接下来又是分析时间复杂度吧，一尘心里想

希尔排序的复杂度和增量序列是相关的

{1,2,4,8,...}这种序列并不是很好的增量序列，使用这个增量序列的时间复杂度（最坏情形）是O(n^2)

Hibbard提出了另一个增量序列{1,3,7，...,2^{k-1}，这种序列的时间复杂度(最坏情形)为O(n}1.5)

Sedgewick提出了几种增量序列，其最坏情形运行时间为O（n^1.3）,其中最好的一个序列是{1,5,19,41,109,...}

对不同增量的复杂度感性趣可以参考《数据结构与算法分析》一书或其他相关论文

四、稳定性

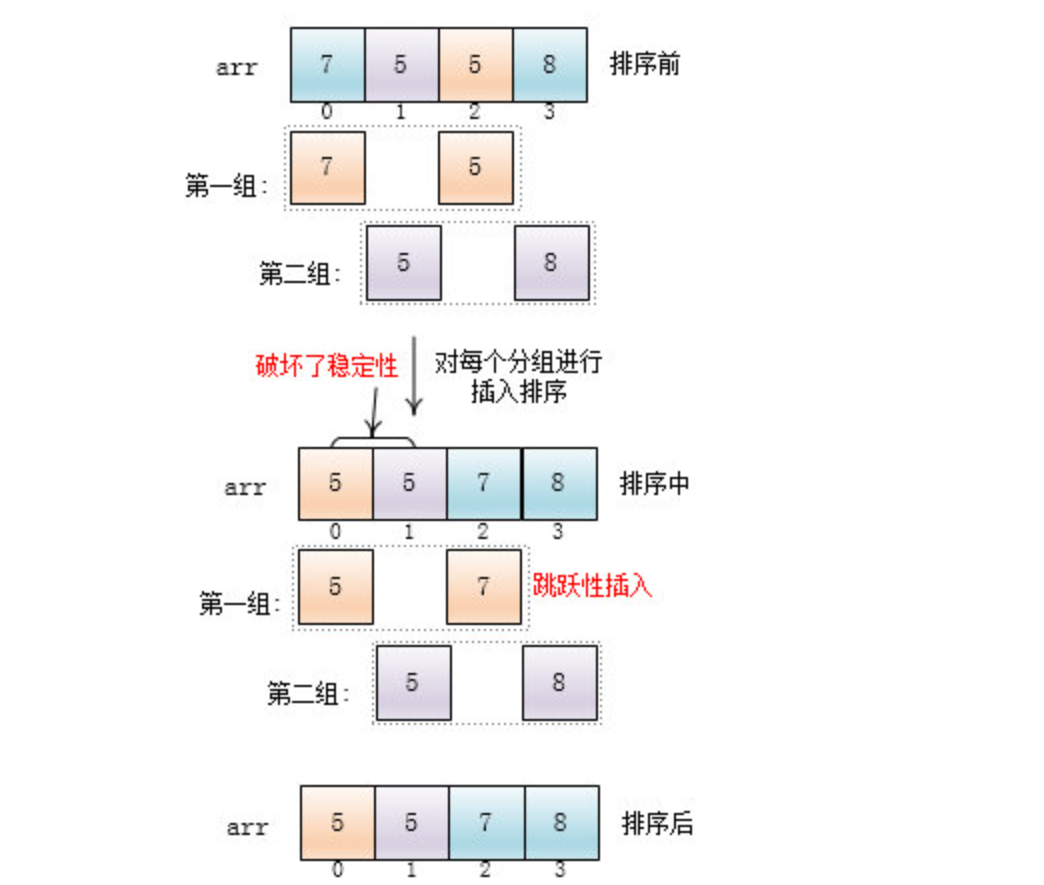
关于稳定性可看：冒泡排序

说完，一尘继续玩起了扑克

标签：插入排序,希尔,分组,增量,漫画,一尘,排序,复杂度
From： https://www.cnblogs.com/kubidemanong/p/17228492.html