KMP的主要思想是当出现字符串不匹配时,可以知道一部分之前已经匹配的文本内容,可以利用这些信息避免从头再去做匹配了。
KMP的精髓所在就是前缀表。(下面用next[] 数组来表示)
- 前缀表:起始位置到下标i之前(包括i)的子串中,有多大长度的相同前缀后缀。
- 前缀:指不包含最后一个字符的所有以第一个字符开头的连续子串。
- 后缀:指不包含第一个字符的所有以最后一个字符结尾的连续子串。
1.next数组
next数组即为前缀表。前缀表表示的是起始位置到下标i之前(包括i)的子串中,有多大长度的相同前缀后缀。只看概念很抽象,但是随便举一个例子就懂了。对于"aabaaf"这个字符串来说,一共有6个子串。包括"a" "aa" "aab" "aaba" "aabaa" "aabaaf",对于这6个子串分别求最大长度相同前后缀:
|
"a" |
0 |
|
"aa" |
1 |
|
"aab" |
0 |
|
"aaba" |
1 |
|
"aabaa" |
2 |
|
"aabaaf" |
0 |
由此可得next数组的值:[0, 1, 0, 1, 2, 0]。
2.KMP的原理
要理解KMP前缀表的作用,必须先搞清楚KMP方法的底层原理。
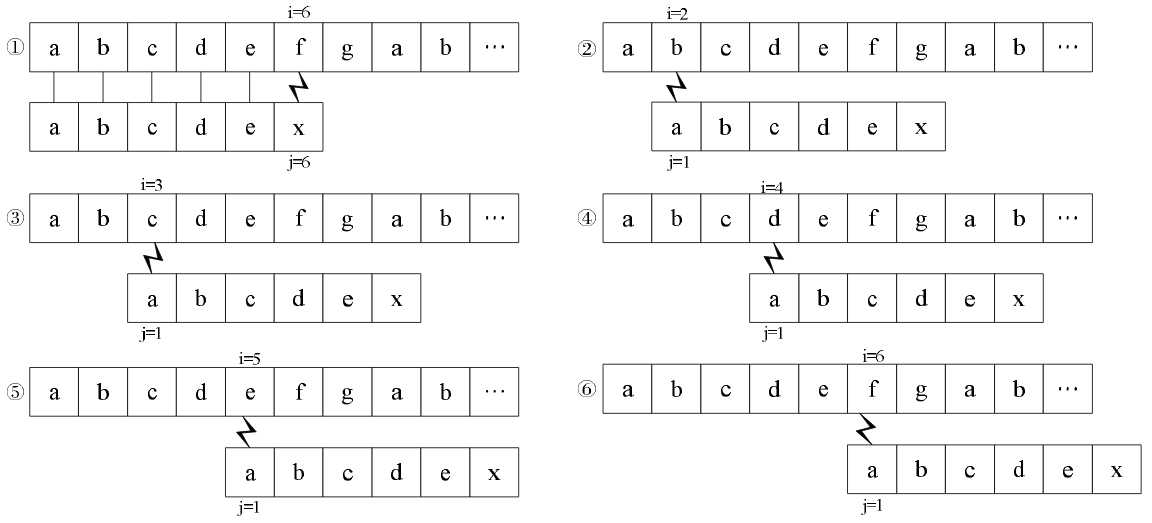
"abcdex" 对应next数组 [0, 0, 0, 0, 0, 0]
首先看上面这张图,按照暴力比较法,进行过比较①之后,应该是流程②③④⑤⑥顺序依次进行。但是我们提前观察子串,知道“abcde”这个字符串压根没有相等前后缀,即最长相等前后缀长度为0。(这里所谓“提前观察”的结果,在代码里就存放在next数组中,next数组第5位值为0)根据这一点,据可以对比较过程进行改进。
为什么要看“abcde”这个子串呢?因为在步骤①中,上下两个字符串的该子串对应相等了。此时再看步骤②,如下图所示:
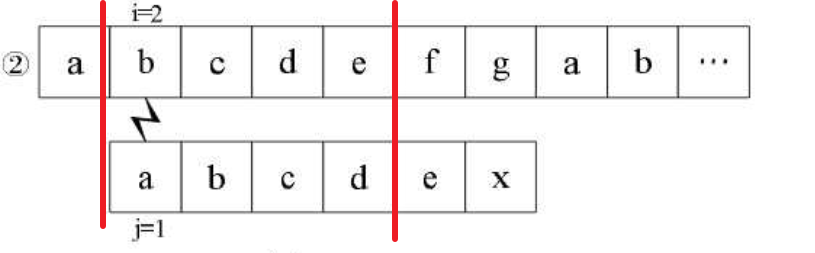
是不是就相当于用“abcde”的4位后缀与其4位前缀相比?但我们已经提前知道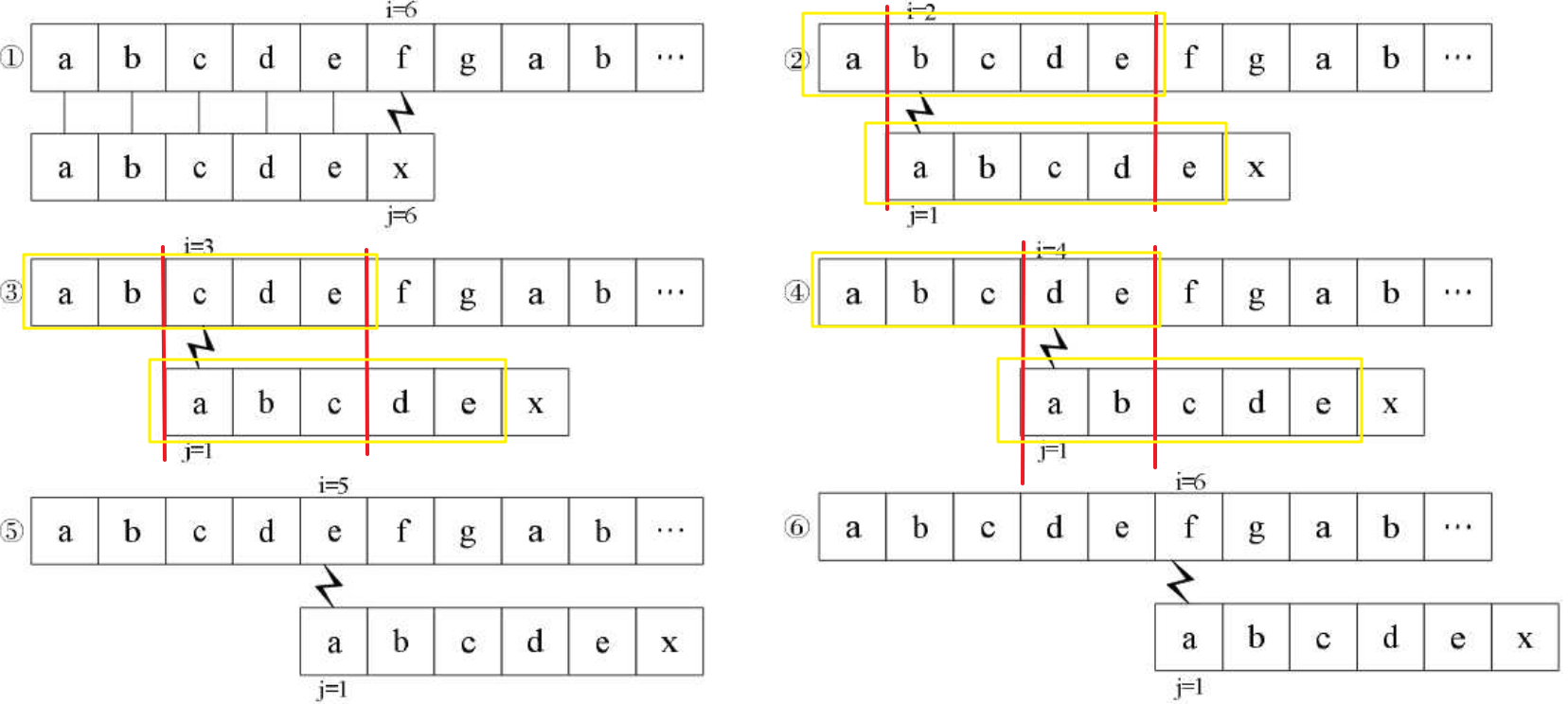
③④⑤也是类似的情况,③是在用“abcde”的3位后缀和3位前缀相比,④是在用“abcde”的2位后缀和2位前缀相比……我们根据
3.另一个例子
再来看一个例子,加深下理解:
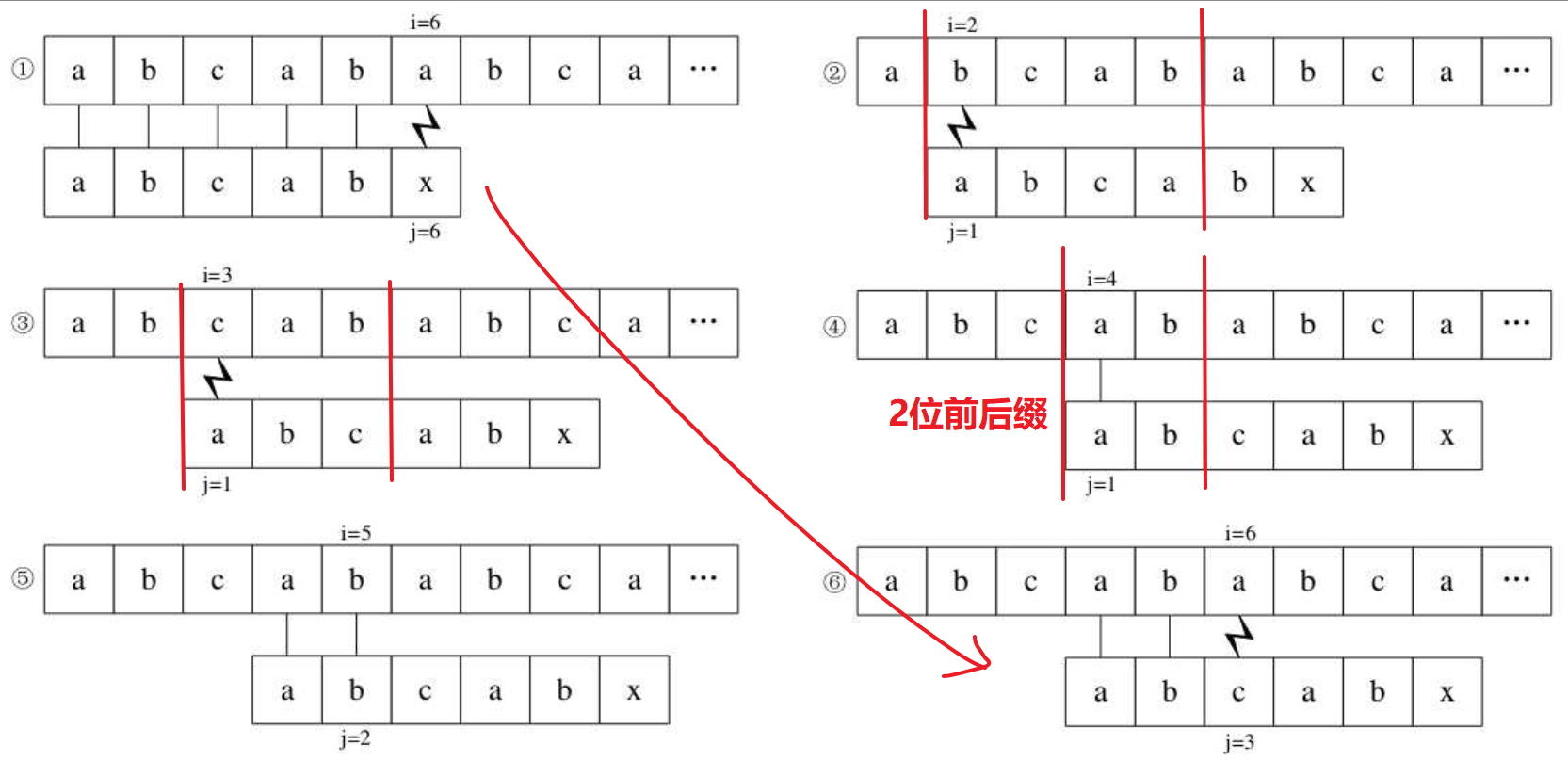
"abcabx" 对应next数组 [0, 0, 0, 1, 2, 0]
提前观察“abcab”这个子串,可知最长相等先后缀长度为2(next数组第5位值为2)。通过这个信息可以得知,在①比较完以后的②③都是无意义的,因为
4.总结
上面的例子其实都是从底层原理的角度出发来进行讲解的,所以笔者故意没有提具体的有关代码的东西,提一下next数组是希望读者能理解其作用,那就是给出 下标对应长度子串的最长相等前后缀的长度。具体的代码实现有许多种,这里不再赘述。其实只要理解底层原理,就不会绕晕了,下面贴出来我的代码实现(参照的代码随想录 hhh)。这段代码里,getNext函数中的第8行,我一开始是不太理解,后面举了一个例子,跟着走了一遍流程就豁然开朗了。其实对一个子串求next数组的过程可以分为两部分:1.是给next数组赋值;2.是利用已经求得的next数组去进行字符串的匹配。这么说可能有点抽象,用下面这个例子自己想一遍就懂了。
- 求next数组实用例子 : “aax aab aax aax aab”
class Solution {
public:
void getNext(int* next, const string& s) {
int j = 0;
next[0] = 0;
for(int i = 1; i < s.size(); i++) {
while (j > 0 && s[i] != s[j]) {
j = next[j - 1];
}
if (s[i] == s[j]) {
j++;
}
next[i] = j;
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) {
return 0;
}
int next[needle.size()];
getNext(next, needle);
int j = 0;
for (int i = 0; i < haystack.size(); i++) {
while(j > 0 && haystack[i] != needle[j]) {
j = next[j - 1];
}
if (haystack[i] == needle[j]) {
j++;
}
if (j == needle.size() ) {
return (i - needle.size() + 1);
}
}
return -1;
}
};
标签:子串,前缀,后缀,needle,next,算法,数组,KMP,底层 From: https://www.cnblogs.com/astro1125/p/16705185.html