435. 无重叠区间
题目链接:435. 无重叠区间 - 力扣(LeetCode)
思路
这道题首先进行排序,使得相邻的区间紧挨在一起。按左边界或者右边界都可以。
其次定义一个变量result记录重叠的数目,当确定区间有重叠时,result++,同时取这两个区间右边界的最小的一个即可。
代码
按右边界排序
1 class Solution {
2 public int eraseOverlapIntervals(int[][] intervals) {
3 Arrays.sort(intervals, (a,b)-> {
4 return Integer.compare(a[0],b[0]);
5 });
6 int count = 1;
7 for(int i = 1;i < intervals.length;i++){
8 if(intervals[i][0] < intervals[i-1][1]){
9 intervals[i][1] = Math.min(intervals[i - 1][1], intervals[i][1]);
10 continue;
11 }else{
12 count++;
13 }
14 }
15 return intervals.length - count;
16 }
17 }
按左边界排序
1 class Solution {
2 public int eraseOverlapIntervals(int[][] intervals) {
3 Arrays.sort(intervals, (a,b)-> {
4 return Integer.compare(a[0],b[0]);
5 });
6 int remove = 0;
7 int pre = intervals[0][1];
8 for(int i = 1; i < intervals.length; i++) {
9 if(pre > intervals[i][0]) {
10 remove++;
11 pre = Math.min(pre, intervals[i][1]);
12 }
13 else pre = intervals[i][1];
14 }
15 return remove;
16 }
17 }
763.划分字母区间
题目链接:763. 划分字母区间 - 力扣(LeetCode)
思路
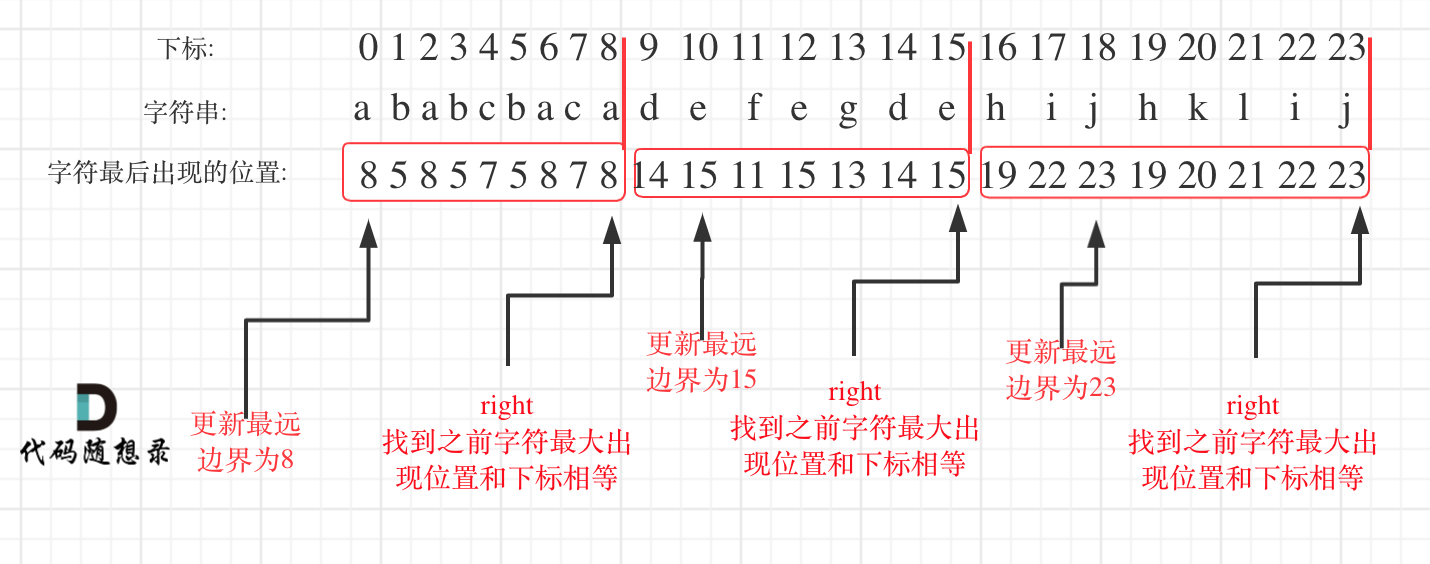
- 首先统计每一个字符最后出现的位置,可以使用hash表操作。
- 随后从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
如图:
代码
1 class Solution {
2 public List<Integer> partitionLabels(String S) {
3 List<Integer> list = new LinkedList<>();
4 int[] edge = new int[26];
5 char[] chars = S.toCharArray();
6 for (int i = 0; i < chars.length; i++) {
7 edge[chars[i] - 'a'] = i;
8 }
9 int idx = 0;
10 int last = -1;
11 for (int i = 0; i < chars.length; i++) {
12 idx = Math.max(idx,edge[chars[i] - 'a']);
13 if (i == idx) {
14 list.add(i - last);
15 last = i;
16 }
17 }
18 return list;
19 }
20 }
1 class Solution{
2 /*解法二: 统计字符串中所有字符的起始和结束位置,记录这些区间,将区间按左边界从小到大排序,找到边界将区间划分成组,互不重叠。找到的边界就是答案。*/
3
4 public int[][] findPartitions(String s) {
5 List<Integer> temp = new ArrayList<>();
6 int[][] hash = new int[26][2];//26个字母2列 表示该字母对应的区间
7
8 for (int i = 0; i < s.length(); i++) {
9 //更新字符c对应的位置i
10 char c = s.charAt(i);
11 if (hash[c - 'a'][0] == 0) hash[c - 'a'][0] = i;
12
13 hash[c - 'a'][1] = i;
14
15 //第一个元素区别对待一下
16 hash[s.charAt(0) - 'a'][0] = 0;
17 }
18
19
20 List<List<Integer>> h = new LinkedList<>();
21 //组装区间
22 for (int i = 0; i < 26; i++) {
23 //if (hash[i][0] != hash[i][1]) {
24 temp.clear();
25 temp.add(hash[i][0]);
26 temp.add(hash[i][1]);
27 //System.out.println(temp);
28 h.add(new ArrayList<>(temp));
29 // }
30 }
31 // System.out.println(h);
32 // System.out.println(h.size());
33 int[][] res = new int[h.size()][2];
34 for (int i = 0; i < h.size(); i++) {
35 List<Integer> list = h.get(i);
36 res[i][0] = list.get(0);
37 res[i][1] = list.get(1);
38 }
39
40 return res;
41
42 }
43
44 public List<Integer> partitionLabels(String s) {
45 int[][] partitions = findPartitions(s);
46 List<Integer> res = new ArrayList<>();
47 Arrays.sort(partitions, (o1, o2) -> Integer.compare(o1[0], o2[0]));
48 int right = partitions[0][1];
49 int left = 0;
50 for (int i = 0; i < partitions.length; i++) {
51 if (partitions[i][0] > right) {
52 //左边界大于右边界即可纪委一次分割
53 res.add(right - left + 1);
54 left = partitions[i][0];
55 }
56 right = Math.max(right, partitions[i][1]);
57
58 }
59 //最右端
60 res.add(right - left + 1);
61 return res;
62
63 }
64 }
56. 合并区间
题目链接:56. 合并区间 - 力扣(LeetCode)
思路
这道题思路为只要存在重叠的区间,都合并成一个大区间,最后记录所有合并出的大区间。
- 首先对所有区间按照起点进行排序,因为最后要输出每个大区间的起点和终点,所以把当前大区间的起点和终点用第一个区间来初始化一下。
- 然后从第二个区间开始遍历,有以下两种情况:
- (1)区间重叠。由于我们是按起点排序的,所以不必更新左边界,它已经是最小值。需要更新右边界为两个区间中的较大值。即,区间取并。
- (2)区间不重叠。那么说明之前的大区间已经无法覆盖新的区间,就把大区间先加入结果集,然后新的大区间的起点和终点用新区间来初始化。
注意,遍历结束后不要忘记把当前大区间加入结果集。一个例子就是数据中只有一个区间的情况。
代码
1 /**
2 时间复杂度 : O(NlogN) 排序需要O(NlogN)
3 空间复杂度 : O(logN) java 的内置排序是快速排序 需要 O(logN)空间
4
5 */
6 class Solution {
7 public int[][] merge(int[][] intervals) {
8 List<int[]> res = new LinkedList<>();
9 //按照左边界排序
10 Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));
11 //initial start 是最小左边界
12 int start = intervals[0][0];
13 int rightmostRightBound = intervals[0][1];
14 for (int i = 1; i < intervals.length; i++) {
15 //如果左边界大于最大右边界
16 if (intervals[i][0] > rightmostRightBound) {
17 //加入区间 并且更新start
18 res.add(new int[]{start, rightmostRightBound});
19 start = intervals[i][0];
20 rightmostRightBound = intervals[i][1];
21 } else {
22 //更新最大右边界
23 rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);
24 }
25 }
26 res.add(new int[]{start, rightmostRightBound});
27 return res.toArray(new int[res.size()][]);
28 }
29 }
30
31 }
1 // 版本2
2 class Solution {
3 public int[][] merge(int[][] intervals) {
4 LinkedList<int[]> res = new LinkedList<>();
5 Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
6 res.add(intervals[0]);
7 for (int i = 1; i < intervals.length; i++) {
8 if (intervals[i][0] <= res.getLast()[1]) {
9 int start = res.getLast()[0];
10 int end = Math.max(intervals[i][1], res.getLast()[1]);
11 res.removeLast();
12 res.add(new int[]{start, end});
13 }
14 else {
15 res.add(intervals[i]);
16 }
17 }
18 return res.toArray(new int[res.size()][]);
19 }
20 }
1 // 版本三
2 class Solution {
3 public int[][] merge(int[][] intervals) {
4 if(intervals.length == 0)
5 return new int[0][2];
6 //排序
7 Arrays.sort(intervals,new Comparator<int[]>(){
8 public int compare(int[] intervals1,int[] intervals2){
9 return intervals1[0] - intervals2[0];
10 }
11 });
12 ArrayList<int[]> merged = new ArrayList<>();
13 //合并
14 for(int i = 0;i < intervals.length;i++){
15 //取当前二维数组中的两个元素
16 int left = intervals[i][0],right = intervals[i][1];
17 if(merged.size() == 0 || merged.get(merged.size() - 1)[1] < left){
18 merged.add(new int[]{left,right});
19 }else{
20 merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1],right);
21 }
22 }
23 return merged.toArray(new int[merged.size()][]);
24 }
25 }
标签:Day36,res,随想录,++,int,intervals,区间,new From: https://www.cnblogs.com/xpp3/p/17195856.html