首页 > 编程语言 >2023算法笔记

2023算法笔记

时间：2023-02-24 20:02:09浏览次数：36  
标签：loc key int mid 笔记 算法 数组 2023 排序

Hoppz算法笔记

前言 2023_02_18

还是太菜了，笔记基于 《算法导论》 && 《数据结构与算法分析 C++描述》，想着为复试准备（虽然很大程度上今年是考不上了），就开始重看算法导论，前几年大致翻过几页，感觉数学证明太多直接放弃了，想着学了一点微积分，线代，概率论的知识（虽然学的不好，但总是有点基础了）就又开始看了

1、基础知识

1.1、排序算法

1.1.1、插入排序(insertionsort)

插入排序与我们整理扑克牌类似。

开始时，我们左手为空并且桌子上的牌面向下（意思就是我们并不会在意牌出现的顺序）。然后，我们每次从桌子上拿走一张牌并将它插入左手正确的位置。《算法导论》p10

image-20230219105815401

void insertion_sort_ascend(vector<int> &vec)
{
    if( vec.size() == 1 ) return ;

    for(int j = 1; j < vec.size(); j++){

        int key = vec[j];

        // insert a[j] intro sorted sequence a[1...j-1];

        int i = j - 1;
        while( i >= 0 && vec[i] > key ){
            vec[i + 1] = vec[i];
            i--;
        }
        vec[i + 1] = key;
    }
}

void insertion_sort_descend(vector<int> &vec)
{
    if( vec.size() == 1 ) return ;

    for(int j = 1; j < vec.size(); j++){

        int key = vec[j];

        int i = j - 1;
        while( i >= 0 && vec[i] < key ){
            vec[i + 1]  = vec[i];
            i--;
        }
        vec[i+1] = key;
    }
}

1.1.2、冒牌排序(bubblesort)

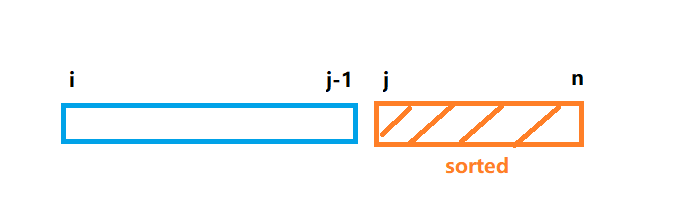
在插入排序（Ascend版本）中 unsorted 数组中的 key 会与 sorted中的数字交换，找到它在 sorted 数组中的正确位置。冒泡排序则是把unsorted 数组中的最大值交换到 j-1 的位置且 \([j-1,n]\) 形成新的 sorted 数组。

image-20230220143900932

void Bubble_Sort(vector<int> &a)
{
    for(int i = a.size() - 1; i > 0 ; i--){

        for(int j = 1 ; j <= i ; j++){
            if( a[j-1] > a[j] ) swap(a[j-1],a[j]);
        }
    }
}

1.1.3、选择排序(selectionsort)

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

void Selection_Sort(vector<int> &a)
{
    for(int i = 0; i < a.size() ; i++ ){

        int mi_loc = i;

        for(int j = i + 1; j < a.size() ; j++){
            if( a[j] < a[mi_loc] ) mi_loc = j;
        }
        swap(a[i],a[mi_loc]);
    }
}

1.1.4、希尔排序

1.1.5、归并排序(megersort)

许多有用的算法在结构上是递归的：为了解决一个 给定的问题，算法一次或多次递归地调用其自身以解决紧密相关的若干子问题。

这些算法典型地遵循分治的思想：

将原问题分解为几个规模较小但类似于原问题的子问题，递归的求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

分治模式在每层递归时都有三个步骤：

  • 分解原问题为若干子问题，这些子问题都是原问题的规模较小的实例。
  • 解决这些子问题，递归地求解各子问题。然而，若子问题的规模足够小，则直接求解。
  • 合并这些子问题的解成原问题的解。

归并排序算法完全遵循分治模式。直观上其操作如下：

  • 分解：分解待排序的 \(n\) 个元素的序列成各具 \(\frac{n}{2}\) 个元素的两个子序列
  • 解决：使用归并排序递归的排序两个序列
  • 合并：合并两个已排序的子序列以产生排序答案

当排序的序列长度为1时，递归开始回升，在这种情况下不需进行任何操作，因为长度为 \(1\) 的每个序列都已排好序。

详细操作见 《算法导论》-p17

带哨兵的merge

注意： 使用 vector 初始化第一个迭代器不用 +1 ，后面一个迭代器要 +1

const int inf = 0x3f3f3f3f;
void merge(vector<int> &a,int p, int q,int r)
{
    vector<int> v1(a.begin()+p,a.begin()+q + 1);
    vector<int> v2(a.begin()+q+1,a.begin()+r + 1);
    v1.push_back(inf),v2.push_back(inf);

    int i = p,v1_loc = 0, v2_loc = 0;
    while(i <= r){

        if( v1[v1_loc] <= v2[v2_loc] ){
            a[i++] = v1[v1_loc++];
        } else {
            a[i++] = v2[v2_loc++];
        }
    }
}

void merge_sort(vector<int> &a,int p, int r)
{
    if(p < r){
        int q = (p + r) >> 1;

        merge_sort(a,p,q);
        merge_sort(a,q+1,r);
        merge(a,p,q,r);
    }
}

不带哨兵的 merge

void merge(vector<int> &a,int p, int q,int r)
{
    vector<int> v1(a.begin()+p,a.begin()+q + 1);
    vector<int> v2(a.begin()+q+1,a.begin()+r + 1);

    int i = p,v1_loc = 0, v2_loc = 0;
    while(i <= r && v1_loc < v1.size() && v2_loc < v2.size() ){

        if( v1[v1_loc] <= v2[v2_loc] ){
            a[i++] = v1[v1_loc++];
        } else {
            a[i++] = v2[v2_loc++];
        }
    }
    if( v1_loc != v1.size() )  while( i <= r) a[i++] = v1[v1_loc++];
    if( v2_loc != v2.size() )  while( i <= r) a[i++] = v2[v2_loc++];

}

2.1.2.1、归并排序解决逆序对问题

假设 \(A[1..n]\) 是一个有 \(n\) 个不同数的数组。若 \(i<j\) 且 \(A[i]>A[j]\)，则对偶 \((i,j)\) 称为 \(A\) 的一个 逆序对

  1. 由集合 \(\{1,2,···,n\}\) 构成的什么数组具有最多逆序对？

    • 降序排列的数组具有最多的逆序对，共 \(\frac{n(n-1)}{2}\) 对。

  2. 插入排序的运行时间与输入数组中逆序对的数量之间是什么关系？

    • 插入排序的主要思想讲数组分为 sorted 数组和 unsorted 数组，当我们处理到 j 元素时 while 循环中 \(a[i]\) 与 \(a[i+1]\) 交换的次数即为逆序对的数量

  3. 使用归并排序来处理逆序对问题

    • 逆序对的核心思想是，找到这个数之前有多少个比它大的数。

      在一次 merge 操作中（已没有哨兵的版本为例），在归并的过程中右边的数组存在比左边数组小的时候，那么在左边数组中剩下的元素都是此时右边的这个数的逆序数，所有我们在代码中只用加一个计数器就可以了。

      image-20230219160108782

1.1.6、堆排序(heapsort)

与归并排序一样，但不同于插入排序的是，堆排序的时间复杂度是 \(\Theta(n \lg_{}{n})\) 。

而与插入排序一样，但不同于归并排序的是，堆排序同样具有具有原址空间性：任何时候都只需要常数个额外的元素空间储存临时的数据。因此，堆排序是集合了我们前面两种排序算法优点的一种排序算法。

  1. （二叉）堆是一个数组，可以被看成一个近似的完全二叉树。

  2. 二叉堆可以分为两种形式：最大堆和最小堆

    最大堆：除了根节点都要满足

    \[A[Parent(i)]\ge A[i] \]

    最小堆：除了根节点都要满足

    \[A[Parent(i)]\le A[i] \]

    在堆排序中，我们使用的是最大堆，最小堆通常用于构造优先队列

image-20230220191028593

int heap_size;

void Max_Heapify(int a[],int i)
{
    int l_son = i<<1;
    int r_son = i<<1|1;

    int max_loc;
    if( l_son <= heap_size && a[i] < a[l_son] ) max_loc = l_son;
    else max_loc = i;

    if( r_son <= heap_size && a[max_loc] < a[r_son] ) max_loc = r_son;

    if(max_loc != i){
        swap(a[max_loc],a[i]);
        Max_Heapify(a,max_loc);
    }
}

void Build_Heap(int a[])
{
    for(int i = (heap_size>>1)+1; i > 0 ; i-- ) Max_Heapify(a,i);
}

void Heap_Sort(int a[])
{
    Build_Heap(a);
    for(int i = heap_size ; i >= 2; i--){
        swap(a[1],a[i]);
        heap_size--;
        Max_Heapify(a,1);
    }
}

1.1.6.1、最大优先队列

image-20230221154204891

int heap_size;
int Heap_Maximum(int a[]){return a[1];}

void Max_Heapify(int a[],int i)
{
    int l_son = i<<1;
    int r_son = i<<1|1;

    int max_loc;
    if( l_son <= heap_size && a[l_son] > a[i] ) max_loc = l_son;
    else max_loc = i;
    if( r_son <= heap_size && a[r_son] > a[max_loc] ) max_loc = r_son;

    if( max_loc != i ){
        swap(a[i],a[max_loc]);
        Max_Heapify(a,max_loc);
    }
}

int Heap_Extract_Max(int a[])
{
    if( heap_size < 1 ) return -0x3f3f3f3f;
    int Max = a[1];

    a[1] = a[heap_size--];
    Max_Heapify(a,1);
    return Max;
}

void Heap_Increase_Key(int a[],int i,int key)
{
    if( key < a[i] ) return ;
    a[i] = key;
    int parent_loc = i >> 1;
    // 插入排序的思想
    while( parent_loc >= 1 && a[i] > a[parent_loc] ){
        swap(a[i],a[parent_loc]);
        i = parent_loc;
        parent_loc = i >> 1;
    }
}

void Heap_Max_Insert(int a[],int key)
{
    a[++heap_size] = -0x3f3f3f3f;
    Heap_Increase_Key(a,heap_size,key);
}

1.1.6.2、最小优先队列

int heap_size;
int Heap_Minimum(int a[]){return a[1];}

void Min_Heapify(int a[],int i)
{
    int l_son = i<<1;
    int r_son = i<<1|1;

    int max_loc;
    if( l_son <= heap_size && a[l_son] < a[i] ) max_loc = l_son;
    else max_loc = i;
    if( r_son <= heap_size && a[r_son] < a[max_loc] ) max_loc = r_son;

    if( max_loc != i ){
        swap(a[i],a[max_loc]);
        Min_Heapify(a,max_loc);
    }
}

int Heap_Extract_Min(int a[])
{
    if( heap_size < 1 ) return -0x3f3f3f3f;
    int Max = a[1];

    a[1] = a[heap_size--];
    Min_Heapify(a,1);
    return Max;
}

void Heap_Decrease_Key(int a[],int i,int key)
{
    if( key > a[i] ) return ;
    a[i] = key;
    int parent_loc = i >> 1;
    while( parent_loc >= 1 && a[i] < a[parent_loc] ){
        swap(a[i],a[parent_loc]);
        i = parent_loc;
        parent_loc = i >> 1;
    }
}

void Heap_Min_Insert(int a[],int key)
{
    a[++heap_size] = 0x3f3f3f3f;
    Heap_Decrease_Key(a,heap_size,key);
}

1.1.7、快速排序(quicksort)

与归并排序一样，快速排序也使用了分治的思想。下面是对一个典型的子数组 \(A[l..r]\) 进行快速排序的三步分治过程：

  • 分解：数组 \(A[l..r]\) 被划分为两个（可能为空）子数组 \(A[l..mid]\) 和 \(A[mid+1..r]\)，两数组要满足第一个数组要小于等于一个给定的 key（一般为 a[mid] or a[l] or a[r]） ，第二个数组大于等于 key 。
  • 解决：通过递归调用快速排序，对子数组 \(A[l..mid]\) 和 \(A[mid+1..r]\) 进行排序。
  • 合并：因为子数组都是原址排序的（没有产生额外的空间），所以不需要合并操作。

下面算法与书上的代码不同，书上的算法当数据全为同一个数时，无法进一步划分数组。（思考7-2）

下面代码采用的是思考7-1 的 Hoare 划分

int Partition_Hoare(int a[],int l,int r)
{
    int i = l - 1, j = r + 1,key = a[ (l+r)>>1 ];
    while(true ){
        // 这里不能写 <= 以及 >= 如 3 3 1 2 2
        // 当最小值为 key 时，第一轮 j 会一直减到 -1
        do{i++;}while( a[i] < key );
        do{j--;}while( a[j] > key );
        if( i < j ) swap(a[i],a[j]);
        else return j;
    }
}

void Quick_Sort(int a[],int l,int r)
{
    if( l < r ){
        int mid = Partition_Hoare(a,l,r);
        Quick_Sort(a,l,mid);
        Quick_Sort(a,mid+1,r);
    }
}

1.1.7.1、快速选择排序

相当于 nth_elment() 在 \(\Theta(n)\) 的时间内返回这个数组第 \(k\) 小的数

Quick_Sort() 中的递归边界非常重要！！

int Partition_Hoare(int a[],int l,int r)
{
    int i = l - 1, j = r + 1, key = a[ (l+r)>>1 ];
    while(true){
        do{i++;}while( a[i] < key );
        do{j--;}while( a[j] > key );

        if( i < j ) { swap( a[i],a[j] ); }
        else return j;
    }
}

int Quick_Sort(int a[],int l,int r,int k)
{
    if( l >= r ) return a[l];

    int j = Partition_Hoare(a,l,r);
    // 如果 k 在前段内
    if( j - l + 1 >= k ) return Quick_Sort(a,l,j,k);
    else return Quick_Sort(a,j+1,r, k - (j - l + 1) );
}

1.1.8、计数排序(countsort)

计数：记录比数小的数有多少个

计数排序的基本思想是：

对每一个输入元素 \(x\) ，确定小于 \(x\) 的元素的个数。

利用这一信息，就可以直接 \(x\) 放到它在输出数组中的位置上了。当有几个元素相同时u，这一方案要略做修改。

我们需要首先给出当前数组的最大值以及数组的大小，还需要两个辅助数组。

void Count_Sort(int a[],int Max,int Size)
{
    // 记录大小为 a[i] 的数出现了多少次
    for(int i = 1 ; i <= Size ; i++) cnt[ a[i] ]++;
    // 有多少小于等于这个数的数
    for(int i = 1 ; i <= Max ; i++) cnt[i] += cnt[i-1];
    
    // 如果是正序的遍历是正确的，但不稳定
    for(int i = Size; i >= 1 ; i-- ){
        ans[ cnt[ a[i] ] ]= a[i];
        --cnt[ a[i] ];
    }
}

1.1.9、基数排序

1.1.10、桶排序

1.1.11、排序后记

插入排序、归并排序、堆排序及快速排序都是比较排序算法:它们都是通过对元素进行比较操作来确定输入数组的有序次序。

我们可以证明任意比较排序算法排序 \(n\) 个元素的最坏情况运行时间的下界为 \(\Theta(n\lg_{}{n} )\) ，从而证明堆排序和归并排序是渐近最优的比较排序算法。

image-20230220151450191

1.2、分治算法

分治方法将问题划分为互不相交的子问题，递归地求解子问题，再将它们的解组合起来，求出原问题的解。

在分治策略中，我们递归地求解一个问题,在每层递归中应用如下三个步骤：

分治模式在每层递归时都有三个步骤：

  • 分解原问题为若干子问题，这些子问题都是原问题的规模较小的实例（分解到不可再分的基问题，也就是递归的边界）。
  • 解决这些子问题，递归地求解各子问题。然而，若子问题的规模足够小，则直接求解。
  • 合并这些子问题的解成原问题的解。

当子问题足够大，需要递归求解时，我们称之为递归情况。当子问题变得足够小，不再需要递归时，我们说递归已经触底，进入了基本情况。

传统上，在其代码中至少含有两个递归调用的例程叫作分治算法，而代码中只含一个递归调用的例程不是分治是分治算法。我们一般坚持子问题是不相交的（即基本上不重叠）。

1.2.1、最大子数组

在数组 \(A[1···n]\) 中寻找和最大的非空连续子数组

image-20230220120835867

暴力算法

对于一段 \(n\) 天的日期，我们需要检查 \(\binom{n-1}{2} =\Theta (n^2)\) 个子数组，分别求和比较其值，求和的过程可以用前缀和数组来优化到 \(\Theta(n)\) 的初始化，每一次查询是 \(O(1)\) 的，依然是 \(\Theta(n^2)\) 的算法。

使用分治策略的求解方法

使用分治策略意味着我们要将子数组划分为两个规模尽量相等的子数组。也就是说，找到子数组的中央位置 \(mid\) ，考虑求解两个子数组 \(A[l,mid],A[mid+1,r]\)。 \(A[l,r]\) 的所有连续子数组所处的位置必然属于下面三种情况之一：

  • 完全位于 \(A[l,mid]\) 中
  • 完全位于 \(A[mid+1,r]\) 中
  • 跨越了中点的子数组。

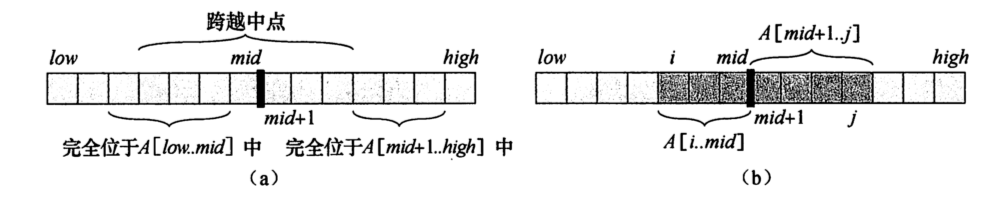
image-20230220121907745

所以，最大子数组也只会属于这三种情况之一。前两种情况可以递归的求解。

对于第三种情况，对于左边的数组，右端点一定是 \(mid\) ，左端点为 \(mid\) 到 \(l\) 其中的任意一个数，所以这一段的值就可以线性求解了。对于右边也是同样的情况。

int Find_Max_Crossing_Subarray(int a[],int l,int r)
{
    int mid = l + r >> 1;
    int l_max = -0x3f3f3f3f,r_max = -0x3f3f3f3f,l_sum = 0,r_sum =0;
    // find max subarray in left side
    for(int i = mid ; i >= l ; i --) {
        l_sum += a[i];
        l_max = max(l_max,l_sum);
    }
    // find max subarray in right side
    for(int i = mid+1 ; i <= r; i ++){
        r_sum += a[i];
        r_max = max(r_max,r_sum);
    }
    return l_max+r_max;
}

int Find_Maximum_Subarray(int a[],int l,int r)
{
    if( l >= r ) return a[l];
    int mid = l + r >> 1;
    int mid_sum = Find_Max_Crossing_Subarray(a,l,r);
    int l_sum = Max_Sequence(a,l,mid);
    int r_sum = Max_Sequence(a,mid+1,r);
    return max({mid_sum,l_sum,r_sum});
}

1.3、贪婪算法

1.4、动态规划

动态规划 Dynamic Programming 与分治方法相似，都是通过组合子问题的解来求解原题（这里，Programming 指的是一种表格法，并非编写计算机程序），与分治的问题划分方法将问题划分为互不相交的子问题不同的是，动态规划应用于子问题重叠的情况，即不同的子问题具有公共的子子问题（子问题的求解是递归进行的，将其划分为更小的子子问题）。

标签：loc,key,int,mid,笔记,算法,数组,2023,排序
From： https://www.cnblogs.com/hoppz/p/17152958.html

相关文章

  • 极光笔记 | 埋点体系建设与实施方法论
    PART 01 前言随着网络技术的发展，从粗犷型到精细化运营型，再到现在的数字化运营，数据变得越来越细分和重要，不仅可以进行策略调整，还可以实现自动化的精细化运营。而数据价值......
  • 2023 syzx 春季训练 1
    得找个时间把zr题补补。。A考虑\(f_{i}\)只能拆为\(f_{i-1}+f_{i-2}\)，考虑拆\(f_{i-1}=f_{i-2}+f_{i-3}\)时，这条\(f_{i-2}-f_{i-3}\)的边在另一种方案时还是......
  • 极光笔记 | 埋点体系建设与实施方法论
    PART01前言随着网络技术的发展，从粗犷型到精细化运营型，再到现在的数字化运营，数据变得越来越细分和重要，不仅可以进行策略调整，还可以实现自动化的精细化运营。而数据价值......
  • 2023.2.24——软件工程日报
    所花时间（包括上课）：8.5h代码量（行）：0行博客量（篇）：5篇今天，上午上了计算机网络和概率论与数理统计，下午上了英语提高与web应用技术开发。我了解到的知识点：1.id、style、class是......
  • J2、ResNet50V2算法实战与解析
     ......
  • 2023/2/24每日总结
    App项目有两个层次第一个层次是项目，另一个层次是模块>模块依附于项目，每个项目至少有一个模块，也能拥有多个模块>一般所言的“编译运行App”，指的是运行某个模块，而非运行某个......
  • Improving Zero-Shot Coordination Performance Based on Policy Similarity 2023-
    基于策略相似度的零样本协调表现改进总结：这篇论文本质上是研究智能体的泛化性能，文中涉及的问题是在一个常规多智能体系统中的智能体如果要与新加入的或者说没有交互过的......
  • m基于改进PSO粒子群优化的RBF神经网络解耦控制算法matlab仿真
    1.算法描述        智能控制的思想最早来自傅京孙教授[，他通过人机控制器和机器人方面的研究，首先把人工智能的自觉推理方法用于学习控制系统，将智能控制概括为自动......
  • 图笔记
    图笔记图的遍历代码结构和回溯代码结构相似，因此在整理回溯题目之后整理了图相关的题目，这部分的题目考察较少，不建议花太多工夫，了解常用的算法即可，力扣周赛后两题极高概率......
  • 2023.2.24总结
    今天课真多，我好累。上午五节课，下午四节课，晚上三节课。累死了，真的快累死了。高级英语课上课听听力，我差点睡着了。今天Javaweb真的啥也没学，真的啥也没学。因为没时间学。对......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99