算法随想Day22【回溯算法】| LC77-组合

回溯算法理论基础

回溯法，一般可以解决如下几种问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等等

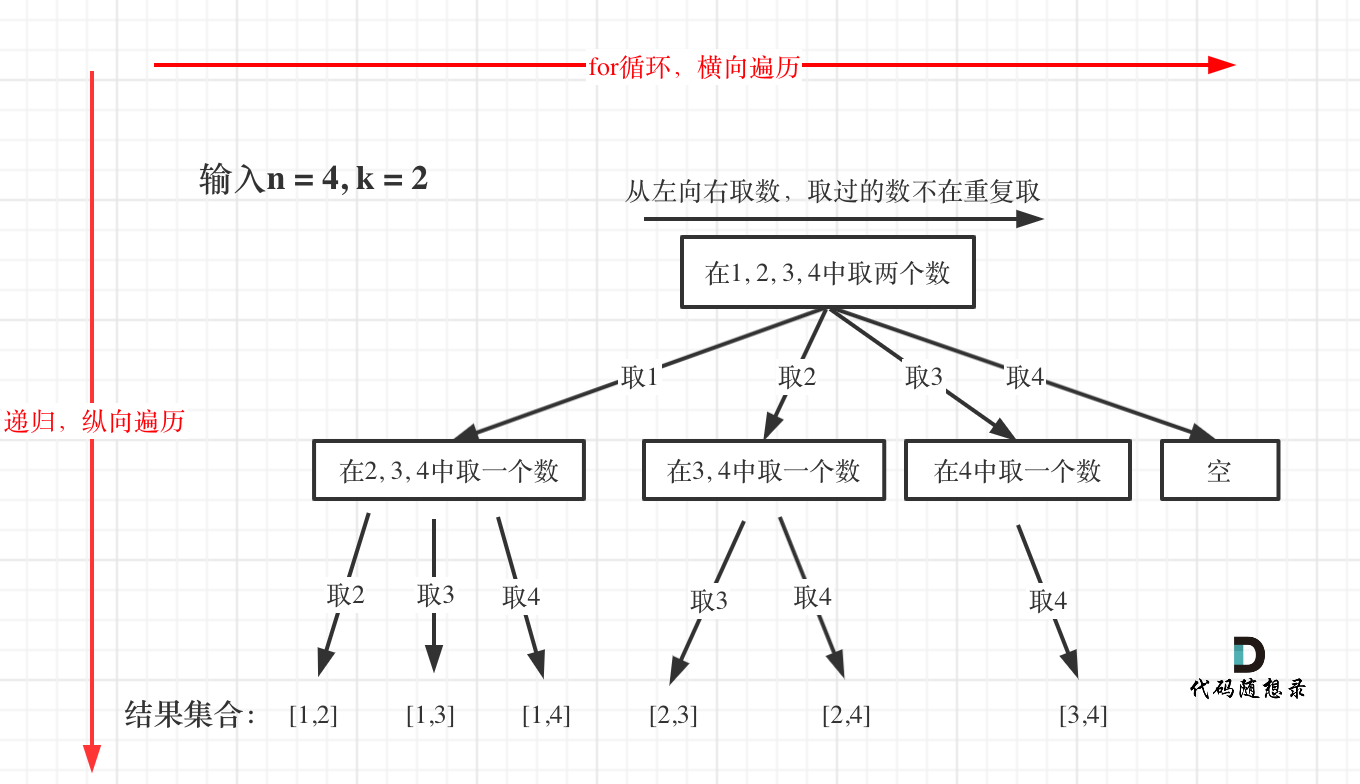
回溯法解决的问题都可以抽象为树形结构

• 树的宽度就是集合的大小

• 树的深度就是递归的深度

回溯算法模板框架如下：

（for循环模拟N叉树的横向遍历，递归模拟N叉树的纵向遍历）

void backtracking(参数) {
    if (终止条件)
    {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）)
    {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

LC77. 组合

学到了上述回溯算法模板，写起来太棒了，参照分析的N叉树路径：

void combineLoop(vector<vector<int>>& result, vector<int>& temp, int left, int& n, int& k)
{
    //vector<int> temp;
    if (temp.size() == k)
    {
        result.push_back(temp);
        return;
    } 
    for (int i = left; i <= n; i++)
    {
        temp.push_back(left);
        combineLoop(result, temp, i + 1, n, k);
        temp.pop_back();
    }
}

vector<vector<int>> combine(int n, int k)
{
    vector<int> temp;
    vector<vector<int>> result;
    combineLoop(result, temp, 1, n, k);
    return result;
}