目录
写在前面
才发现好久没写知识笔记了……
神兵小将真好看,感觉好像年轻了十岁,有一种莫名的沉浸式的体验。
还记得当年特别喜欢那个粉毛来、、、小学生特有的性冲动、、、
简介
暴力 \(O(n^2)\) 求回文子串方法非常简单,枚举回文子串中心向两侧扩展即可,注意特判偶数长度的回文子串。
而 manacher 算法在暴力的基础上,利用了已求得的回文半径加速了比较的过程,使算法可以时空间复杂度均为 \(O(n)\) 级别下完成。
算法流程
以下以模板题:P3805 【模板】manacher 算法 为例。
给定一长度为 \(n\) 的只由小写英文字符构成的字符串 \(s\),求 \(s\) 中最长的回文子串的长度。
\(1\le n\le 1.1\times 10^7\)。
500ms,512MB。
首先在原串的开头、末尾和相邻字符间加入分隔符,使得串长度变为 \(2\times n + 1\)。原串和新串中的回文子串均一一对应,且新串中的回文子串都是有中心奇数长度的串。
考虑在枚举回文子串中心 \(i\) 时维护一个数组 \(p\),\(p_i\) 表示以 \(s_i\) 为中心的最长回文子串的半径长度。即有:
\[p_i = \max(\{x | x\in \N^+, \forall j < x, s_{i - j} = s_{i + j}\}) \]同时维护两个变量 \(pos\) 和 \(r\)。\(r\) 代表以某个位置为中心能扩展到的最靠后的位置,\(pos\) 代表上述的位置,则显然有 \(r=pos + p_{pos}-1\)。显然,对于当前枚举到的回文子串中心 \(i\),由于 \(p_i\ge 1\),则更新 \(p_{i-1}\) 后至少有 \(r = i-1\),则有 \(i\in (pos, r+1]\) 成立。
同时,我们记 \(l=pos - p_{pos}+1\) 代表以 \(pos\) 为中心能扩展到的最靠前的位置。显然,由于 \([l,r]\) 是一个回文串,由对称性,则对于以 \(i\) 为中心的某些回文子串,在 \((l, pos)\) 中一定存在一个 \(j\),满足 \(i + j = 2\times pos\),且以 \(j\) 为中心的某些回文子串与以 \(i\) 为中心的某些回文子串完全相同。如下图所示:
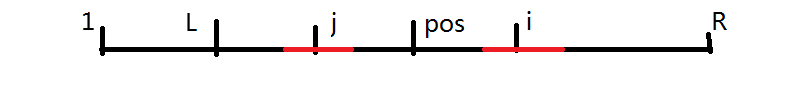
显然,如果我们在计算以 \(i\) 为中心的最长回文子串时,如果可以利用 \(j\) 的信息 \(p_j\),即可避免大量无用的扩展过程。我们考虑 \(p_j\) 的取值对 \(p_i\) 的影响:
- 如果以 \(j\) 为中心的最长回文子串的左端点不会越过 \(l\),即有:\(j - p_j + 1 \ge l\),则 \(p_{i} = p_j\),如下图所示。
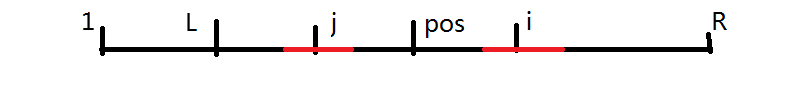
- 如果以 \(j\) 为中心的最长回文子串左端点越过了 \(l\),即有:\(j - p_j + 1 < l\),则 \(p_{i} \ge r - i + 1\),如下图所示。
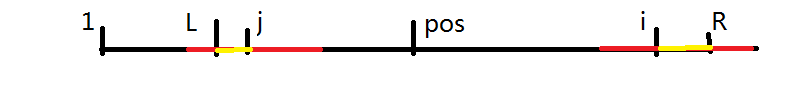
这时我们仅需从第 \(r-i+1\) 位开始以 \(i\) 为中心仅需扩展即可。
再考虑何时应当更新 \(pos\) 的值。我们令 \(pos\) 的初始值为 1,在枚举 \(i\) 过程中,每当计算出一个新的 \(p_i\),就将 \(r' = i + p_i - 1\) 与当前的 \(r\) 进行比较,如果 \(r'>r\),则令 \(pos=i, r = r'\) 即可。
注意求得所有 \(p_i\) 后将其转化为原串的回文串长度。显然,对于以新串中位置 \(i\) 为中心的最长回文子串,对应原串中对应位置长度为 \(p_i - 1\) 的最长回文子串。
代码如下。为了简便记忆,代码中并没有将上述情况 1、2 分开编写,而是均是采用了给 \(p_i\) 赋初始值后再尝试扩展的写法,显然正确性不受影响。
//By:Luckyblock
/*
*/
#include <cstdio>
#include <cctype>
#include <cstring>
#include <algorithm>
const int kN = 1e7 + 1e6 + 10;
//=============================================================
int n, p[kN << 1];
char s[kN], t[kN << 1];
//=============================================================
inline int read() {
int f = 1, w = 0; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = - 1;
for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + ch - '0';
return f * w;
}
//=============================================================
int main() {
scanf("%s", s + 1); n = strlen(s + 1);
for (int i = 1; i <= n; ++ i) t[2 * i - 1] = '%', t[2 * i] = s[i];
t[n = 2 * n + 1] = '%';
int pos = 0, r = 0;
for (int i = 1; i <= n; ++ i) {
p[i] = 1;
if (i < r) p[i] = std::min(p[2 * pos - i], r - i + 1);
while (i - p[i] >= 1 && i + p[i] <= n &&
t[i - p[i]] == t[i + p[i]]) {
++ p[i];
}
if (i + p[i] - 1 > r) pos = i, r = i + p[i] - 1;
}
int maxp = 0;
for (int i = 1; i <= n; ++ i) maxp = std::max(maxp, p[i] - 1);
printf("%d\n", maxp);
return 0;
}
复杂度证明
考虑暴力扩展的过程。发现暴力扩展仅会发生在 \(i>r\),或是 \(j<l\) 时,且都是从 \(i+1\) 开始扩展。
- 当 \(i>r\) 时,暴力扩展后必有 \(i+p_i-1>r\),则必定引起 \(r\) 的右移,右移次数不小于 \(p_i\),即暴力扩展次数 \(-1\)。
- 当 \(j<l\) 时,如果暴力扩展成功,则一定会引起 \(r\) 的右移。右移次数同样等于暴力扩展次数 \(-1\);如果不成功,则 \(r\) 不变。
而 \(r\) 至多仅会更新 \(n\) 次,暴力扩展次数与之同阶也为 \(O(n)\) 级别。同样地,\(i\) 仅会右移 \(n\) 次,则算法的总复杂度为 \(O(n)\) 级别。
写在最后
学完发现这东西好水。
为什么之前不学?因为我觉得 \(O(n\log n)\) 的哈希+二分也挺好/cy
标签:子串,中心,manacher,扩展,pos,笔记,算法,回文 From: https://www.cnblogs.com/luckyblock/p/17044694.html