20.1 NP问题
20.1.1 优化问题和判定问题
一个优化问题往往可以转换成对应的判定问题。一般而言,优化问题时关注某种特殊的结构,并希望优化该结构的某种指标。
Def 20.1 (Clique-优化问题) 给定一个无向图G,如果G的子图H是一个完全图,则称H为G中的一个团。定义一个团的大小为它所含节点的个数。由此定义最大团问题:
- 输入实例:无向图G
- 优化问题:求图G中最大团大小
Def 20.2 (Clique-判定问题)
- 输入实例:无向图G,参数k
- 判定问题:图G中是否存在大小为k的团
20.1.2 P问题的定义
Def 20.3(P问题) 一个问题是P问题,如果存在关于n的一个多项式\(poly(n)\),且存在解决该问题的一个算法,满足算法的代价\(f(n) = O(poly(n))\)。
P问题的关键在于多项式运算的封闭性。
Thm 20.1 最大团问题的优化问题是多项式时间可解的,当且仅当它的判定问题是多项式时间可解的。
20.1.3 NP问题的定义
Def 20.4 (NP问题) 我们定义一个问题为NP问题,如果该问题的解在多项式时间内可验证。这里可验证的含义是首先我们非确定地任意猜测该问题的一个解,其次我们可以在多项式时间内检查这个解是不是该问题的一个解。
Thm 20.2 \(CLIQUE \in NP\)
20.2 问题间的规约
20.2.1 规约的定义
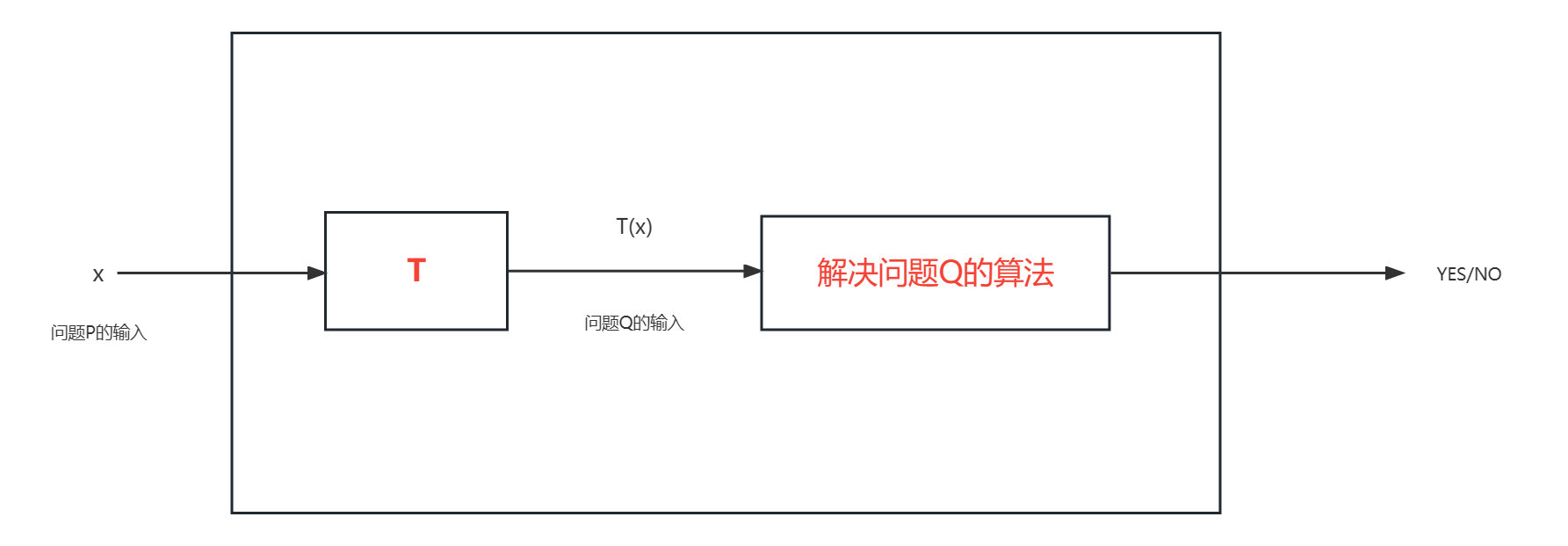
Def 20.5(问题P到Q的规约) 判定问题P到Q的规约(\(P \le Q\))为一个转换函数\(T(x)\)满足:
- 它能够将问题P的任意一个合法输入\(x\)转换成问题Q的一个合法输入\(T(x)\)。假设已经有了解决问题Q的算法,将\(T(x)\)输入到该算法,则得到问题Q的一个输出
- P问题对于任意输入\(x\)的输出是YES,当且仅当问题Q队输入\(T(x)\)的输入是YES。
20.2.2 规约的代价与问题难度的比较
Def 20.6 (多项式时间规约) 如果T是问题P到Q的规约,且T的代价为其输入规模的多项式,则称问题P可以多项式时间规约到问题Q,记为\(P \le_{P} Q\)
Thm 20.3 多项式时间规约关系是一个传递关系,即对于问题P、Q、R, 如果\(P \le_{P} Q\),\(Q \le_{P} R\) 则\(P \le_{P} R\)。
标签:20.1,Ch20,规约,多项式,问题,算法,输入,Def From: https://www.cnblogs.com/nayameow/p/17043849.html