标签：缓存 hash 算法 哈希 一致性 服务器 节点 图片

1、场景描述

1.1 需求

  假设，我们有三台缓存服务器，有3万张图片需要缓存，希望这些图片被均匀的缓存到这3台服务器上，以便它们能够分摊缓存的压力，即我们希望每台服务器能够缓存1万张左右图片，那么，我们应该怎样做呢？

1.2 方法

  如果我们无规律地将3万张图片平均的缓存在3台服务器上，虽然可以满足我们的需求，但是如果这样做，当我们需要访问某个缓存项时，则需要遍历3台缓存服务器，从3万个缓存项中找到我们需要访问的缓存，遍历的过程效率太低，时间太长，也就失去了缓存的意义，缓存的目的就是提高速度，改善用户体验，减轻后端服务器压力，如果每次读取一个缓存，都需要遍历所有缓存服务器所有缓存项，想想就觉得很累，那么，我们该怎么办呢？

  原始的做法是对缓存项的键进行哈希，将hash后的结果对缓存服务器的数量进行取模操作，通过取模后的结果，决定缓存项将会缓存在哪一台服务器上，以刚才描述的场景为例，假设我们使用图片名称作为访问图片的key，假设图片名称是不重复的，那么，我们可以使用公式：hash（图片名称）% N，计算出图片应该存放在哪台服务器上。
  因为图片的名称是不重复的，所以，当我们对同一个图片名称做相同的哈希计算时，得出的结果应该是不变的，如果我们有3台服务器，使用哈希后的结果对3求余，那么余数一定是0、1或者2，如果求余的结果为0， 我们就把当前图片名称对应的图片缓存在0号服务器上，如果余数为1，就把当前图片名对应的图片缓存在1号服务器上，如果余数为2，同理。那么，当我们访问任意一个图片的时候，只要再次对图片名称进行上述运算，即可得出对应的图片应该存放在哪一台缓存服务器上，我们只要在这一台服务器上查找图片即可，如果图片在对应的服务器上不存在，则证明对应的图片没有被缓存，也不用再去遍历其他缓存服务器了
  通过这样的方法，即可将3万张图片随机的分布到3台缓存服务器上了，而且下次访问某张图片时，直接能够判断出该图片应该存在于哪台缓存服务器上，这样就能满足我们的需求了，我们暂时称上述算法为HASH取模算法，过程可以用下图表示：

  但是，使用上述HASH算法进行缓存时，会不会有缺陷？

  如果3台缓存服务器无法满足我们的缓存需求，那么我们应该怎么做呢？没错，很简单，增加服务器，假设我们增加了一台缓存服务器，那么缓存服务器的数量就由3台变成了4台，此时，如果仍然使用上述方法对同一张图片进行缓存，那么这张图片所在的服务器编号必定与原来3台服务器时所在的服务器编号不同，因为除数由3变为了4，被除数不变的情况下，余数肯定不同，这种情况带来的结果就是当服务器数量变动时，所有缓存的位置都要发生改变，所有缓存在一定时间内是失效的，当应用无法从缓存中获取数据时，则会向后端服务器请求数据，
  同理，假设3台缓存中突然有一台缓存服务器出现了故障，无法进行缓存，那么我们则需要将故障机器移除，但是如果移除了一台缓存服务器，那么缓存服务器数量从3台变为2台，如果想要访问一张图片，这张图片的缓存位置必定会发生改变，以前缓存的图片也会失去缓存的作用与意义，由于大量缓存在同一时间失效，造成了缓存的雪崩，此时前端缓存已经无法起到承担部分压力的作用，后端服务器将会承受巨大的压力，整个系统很有可能被压垮。

  使用上述HASH算法会出现的问题：当缓存服务器数量发生变化时，会引起缓存的雪崩，可能会引起整体系统压力过大而崩溃（大量缓存同一时间失效），为了解决这些问题，一致性哈希算法诞生了。

2、基本概念

​  一致性哈希算法实际也是取模算法，只是前面描述的取模算法是对服务器的数量进行取模，而一致性哈希算法是对2^32取模。

2.1hash环

  我们可以把2^32 想象成一个圆，就像钟表一样，钟表是由60个点组成的圆，此处我们把这个圆想象成由2^32个点组成的圆，示意图如下：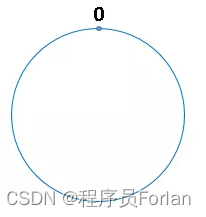

  圆环的正上方的点代表0，0点右侧的第一个点代表1，以此类推，2、3、4、5、6……直到2^32-1 ,0点左侧的第一个点代表2^32-1 ，我们把这个由2^32 个点组成的圆环称为hash环。

2.2 原理

  以之前描述的场景为例，假设我们有3台缓存服务器，服务器A、服务器B、服务器C，用它们各自的IP地址进行哈希计算，使用哈希后的结果对2^32取模，公式如下：
（1）hash（服务器A的IP地址） % 2^32
（2）hash（服务器B的IP地址） % 2^32
（3）hash（服务器C的IP地址） % 2^32
  通过上述公式算出的结果一定分别是一个0到2^32-1 之间的一个整数，使用这个整数代表服务器，服务器就可以映射到这个环上，假设3台服务器映射到hash环上，如下图：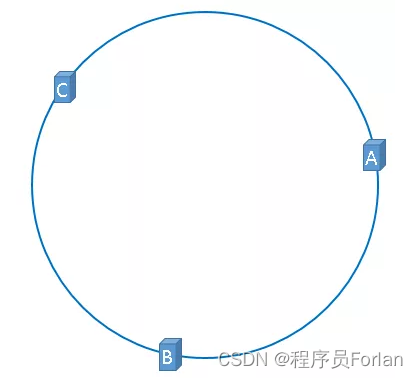

  通过上述方法，把缓存服务器映射到了hash环上，使用同样的方法，将需要缓存的对象映射到hash环上。
  假设，我们需要使用缓存服务器缓存图片，使用图片的名称作为找到图片的key，公式：hash（图片名称） % 2^32，将图片映射到上图中的hash环上，映射后的示意图如下，图中的橘黄色圆形就表示图片：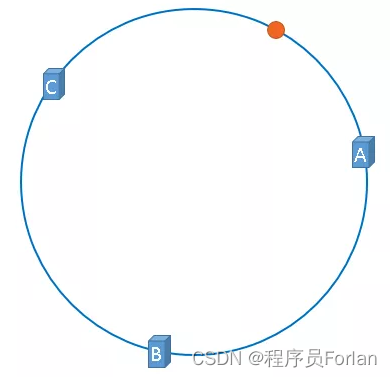

  服务器与图片都被映射到了hash环上，那么上图中的这个图片到底应该被缓存到哪一台服务器上呢？
  上图中的图片将会被缓存到服务器A上，因为从图片的位置开始，沿顺时针方向遇到的第一个服务器就是缓存点，即A服务器，所以，上图中的图片将会被缓存到服务器A上，如下图所示：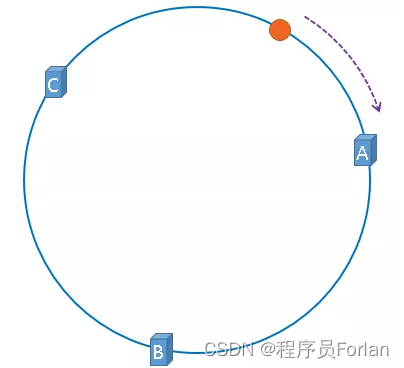

  一致性哈希算法就是通过这种方法，判断一个对象应该被缓存到哪台服务器上的，缓存服务器与被缓存对象都映射到hash环上以后，从被缓存对象的位置出发，沿顺时针方向遇到的第一个服务器，就是当前对象将要缓存于的服务器，由于被缓存对象与服务器hash后的值是固定的，所以，在服务器不变的情况下，一张图片必定会被缓存到固定的服务器上，当下次想要访问这张图片时，只要再次使用相同的算法进行计算，即可算出这个图片被缓存在哪个服务器上，直接去对应的服务器查找对应的图片即可。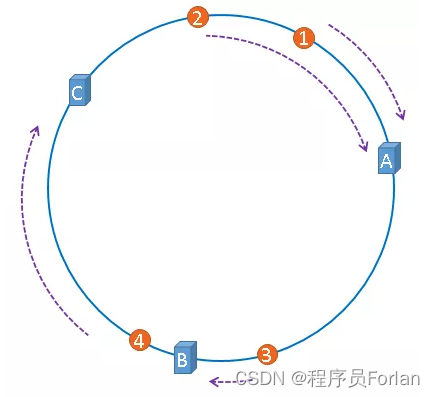

  假设有四张图片需要缓存，示意图如上，1号、2号图片将会被缓存到服务器A上，3号图片将会被缓存到服务器B上，4号图片将会被缓存到服务器C上。

3、优缺点分析

  如果只是简单对服务器数量取模，那么当服务器数量发生变化时，会产生缓存的雪崩，从而很有可能导致系统崩溃，那么使用一致性哈希算法，能够避免这个问题吗？
  假设，服务器B出现了故障，我们现在需要将服务器B移除，那么，我们将上图中的服务器B从hash环上移除即可，移除服务器B以后示意图如下：

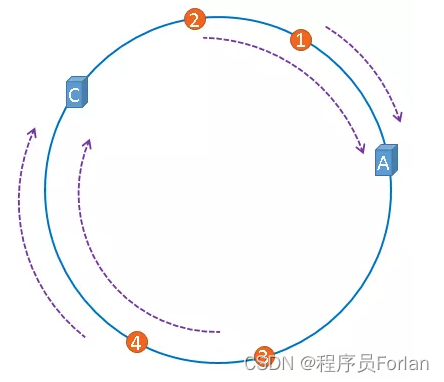
  在服务器B未移除时，图片3应该被缓存到服务器B中，当服务器B移除以后，按照一致性哈希算法的规则，图片3应该被缓存到服务器C中，因为从图片3的位置出发，沿顺时针方向遇到的第一个缓存服务器节点就是服务器C，也就是说，如果服务器B出现故障被移除时，图片3的缓存位置会发生改变。
  但是，图片4仍然会被缓存到服务器C中，图片1与图片2仍然会被缓存到服务器A中，这与服务器B移除之前并没有任何区别，这就是一致性哈希算法的优点，即服务器的数量如果发生改变，并不是所有缓存都会失效，而是只有部分缓存会失效，它并不能杜绝数据迁移的问题，但是可以有效避免数据的全量迁移，需要迁移的只是被移除节点和它上游节点（逆时针最近一个）之间的那部分数据。

4、数据倾斜

在介绍一致性哈希的概念时，我们理想化的将3台服务器均匀的映射到了hash环上，如下图所示：

在实际的映射中，服务器可能会被映射成如下模样：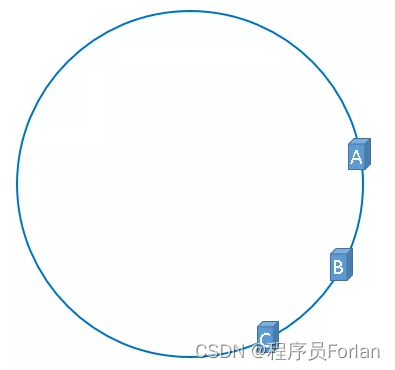

如果服务器被映射成上图中的模样，那么被缓存的对象很有可能大部分集中缓存在某一台服务器上，如下图所示：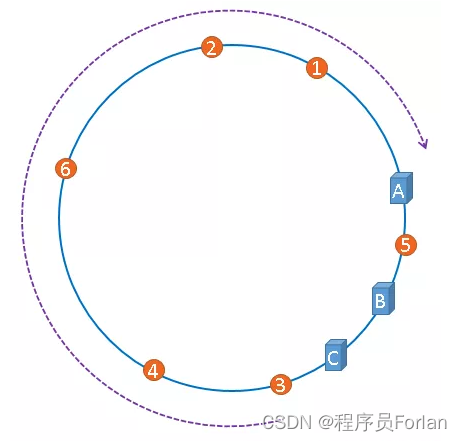

  上图中，1号、2号、3号、4号、6号图片均被缓存在了服务器A上，只有5号图片被缓存在了服务器B上，服务器C上甚至没有缓存任何图片，如果出现上图中的情况，A、B、C三台服务器并没有被合理的平均的充分利用，缓存分布的极度不均匀，而且，如果此时服务器A出现故障，那么失效缓存的数量也将达到最大值，在极端情况下，仍然有可能引起系统的崩溃，上图中的情况被称为数据倾斜，那么，我们应该怎样防止数据倾斜呢？
  那就是加入虚拟节点。

5、虚拟节点

​ 由于我们只有3台服务器，当我们把服务器映射到hash环上时，很有可能出现数据倾斜的情况，缓存往往会极度不均衡的分布在各服务器上，如果想要均衡的将缓存分布在3台服务器上，最好能让这3台服务器尽量多的、均匀的出现在hash环上，但是，真实的服务器资源只有3台，我们怎样凭空的让它们多起来呢，没错，就是凭空的让服务器节点多起来，既然没有多余的真正的物理服务器节点，我们就只能将现有的物理节点通过虚拟的方法复制出来，这些由实际节点虚拟复制而来的节点被称为"虚拟节点"。加入虚拟节点以后的hash环如下：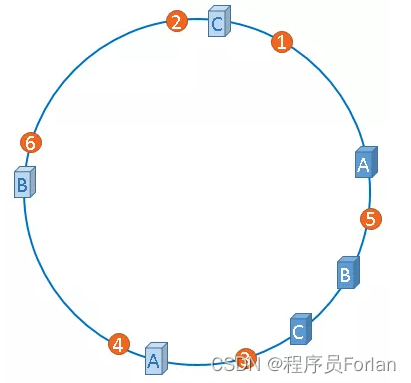

  虚拟节点是物理节点（实际的物理服务器）在hash环上的复制品,一个实际节点可以对应多个虚拟节点
  ​从上图可以看出，A、B、C三台服务器分别虚拟出了一个虚拟节点，如果你需要，也可以虚拟出更多的虚拟节点。
  引入虚拟节点的概念后，缓存的分布就均衡多了，上图中，1号、3号图片被缓存在服务器A中，5号、4号图片被缓存在服务器B中，6号、2号图片被缓存在服务器C中。
  如果你还不放心，可以虚拟出更多的虚拟节点，以便减小数据倾斜所带来的影响，虚拟节点越多，hash环上的节点就越多，缓存被均匀分布的概率就越大。

6、补充总结说明

6.1 虚拟节点设置多少个？

没有必要全部设置成虚拟节点，根据测试结果，看看多少个的效果最好，实现比较均匀

6.2 新加节点，造成部分旧数据无法命中，怎么处理？

原因：新加节点时，获取数据从新新节点获取，但数据还在后面旧节点，还没迁移完成。
解决：获取数据时，可以从顺时针最近的两个节点取，取不到再从数据库获取，会增加复杂度，看场景做取舍。

6.3 一致性hash算法原理

node和data都参与计算，映射到hash环上，node先进行hash得到映射点，新增data时，data进行hash得到数值，找距离最近的node点。

 

标签：缓存,hash,算法,哈希,一致性,服务器,节点,图片
From： https://www.cnblogs.com/huozhonghun/p/16905231.html