dfs序可以\(O(1)\)判断书上两个点的从属关系
Tree Queries
题面翻译
给你一个以\(1\)为根的有根树.
每回询问\(k\)个节点\({v_1, v_2 \cdots v_k}\)
求出是否有一条以根节点为一端的链使得询问的每个节点到此链的距离均\(\leq 1\).
只需输出可行性, 无需输出方案.
题目描述
You are given a rooted tree consisting of\(n\)vertices numbered from\(1\)to\(n\). The root of the tree is a vertex number\(1\).
A tree is a connected undirected graph with\(n-1\)edges.
You are given\(m\)queries. The\(i\)-th query consists of the set of\(k_i\)distinct vertices\(v_i[1], v_i[2], \dots, v_i[k_i]\). Your task is to say if there is a path from the root to some vertex\(u\)such that each of the given\(k\)vertices is either belongs to this path or has the distance\(1\)to some vertex of this path.
输入格式
The first line of the input contains two integers\(n\)and\(m\)(\(2 \le n \le 2 \cdot 10^5\),\(1 \le m \le 2 \cdot 10^5\)) — the number of vertices in the tree and the number of queries.
Each of the next\(n-1\)lines describes an edge of the tree. Edge\(i\)is denoted by two integers\(u_i\)and\(v_i\), the labels of vertices it connects\((1 \le u_i, v_i \le n, u_i \ne v_i\)).
It is guaranteed that the given edges form a tree.
The next\(m\)lines describe queries. The\(i\)-th line describes the\(i\)-th query and starts with the integer\(k_i\)(\(1 \le k_i \le n\)) — the number of vertices in the current query. Then\(k_i\)integers follow:\(v_i[1], v_i[2], \dots, v_i[k_i]\)(\(1 \le v_i[j] \le n\)), where\(v_i[j]\)is the\(j\)-th vertex of the\(i\)-th query.
It is guaranteed that all vertices in a single query are distinct.
It is guaranteed that the sum of\(k_i\)does not exceed\(2 \cdot 10^5\)(\(\sum\limits_{i=1}^{m} k_i \le 2 \cdot 10^5\)).
输出格式
For each query, print the answer — "YES", if there is a path from the root to some vertex\(u\)such that each of the given\(k\)vertices is either belongs to this path or has the distance\(1\)to some vertex of this path and "NO" otherwise.
样例 #1
样例输入 #1
10 6
1 2
1 3
1 4
2 5
2 6
3 7
7 8
7 9
9 10
4 3 8 9 10
3 2 4 6
3 2 1 5
3 4 8 2
2 6 10
3 5 4 7
样例输出 #1
YES
YES
YES
YES
NO
NO
提示
The picture corresponding to the example:
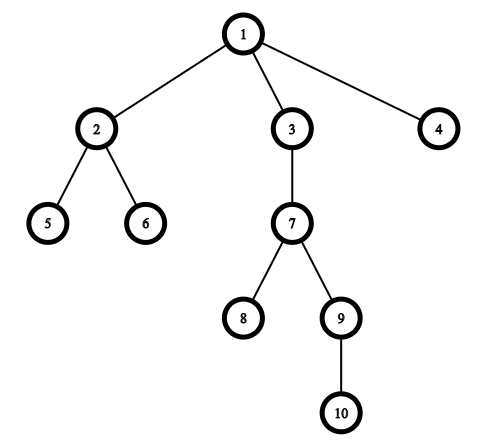
Consider the queries.
The first query is\([3, 8, 9, 10]\). The answer is "YES" as you can choose the path from the root\(1\)to the vertex\(u=10\). Then vertices\([3, 9, 10]\)belong to the path from\(1\)to\(10\)and the vertex\(8\)has distance\(1\)to the vertex\(7\)which also belongs to this path.
The second query is\([2, 4, 6]\). The answer is "YES" as you can choose the path to the vertex\(u=2\). Then the vertex\(4\)has distance\(1\)to the vertex\(1\)which belongs to this path and the vertex\(6\)has distance\(1\)to the vertex\(2\)which belongs to this path.
The third query is\([2, 1, 5]\). The answer is "YES" as you can choose the path to the vertex\(u=5\)and all vertices of the query belong to this path.
The fourth query is\([4, 8, 2]\). The answer is "YES" as you can choose the path to the vertex\(u=9\)so vertices\(2\)and\(4\)both have distance\(1\)to the vertex\(1\)which belongs to this path and the vertex\(8\)has distance\(1\)to the vertex\(7\)which belongs to this path.
The fifth and the sixth queries both have answer "NO" because you cannot choose suitable vertex\(u\).
std
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+9;
int n,m;
int h[N],ver[N<<1],ne[N<<1],idx;
int dep[N],fa[N],dfn[N],sz[N],tim;
int k[N];
void add(int u,int v)
{
idx++,ver[idx] = v,ne[idx] = h[u];h[u] = idx;
}
void dfs(int u,int pre)
{
fa[u] = pre,dfn[u] = ++tim,dep[u] = dep[pre]+1,sz[u] = 1;
for(int i = h[u];i;i= ne[i])
{
int v = ver[i];
if(v == pre)continue;
dfs(v,u);
sz[u] += sz[v];
}
}
bool cmp(int x,int y){return dep[x] > dep[y];}
int main()
{
scanf("%d%d",&n,&m);
for(int i = 1;i < n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v),add(v,u);
}
dfs(1,1);
while(m--)
{
int t;
scanf("%d",&t);
for(int i = 1;i <= t;i++)scanf("%d",&k[i]),k[i] = fa[k[i]];
sort(k+1,k+1+t,cmp);
bool flag = 1;
for(int i = 1;i < t;i++)
{
if(dfn[k[i]] > dfn[k[i+1]]+sz[k[i+1]]-1 || dfn[k[i]] < dfn[k[i+1]])
{
flag = 0;
break;
}
}
if(flag)printf("YES\n");
else printf("NO\n");
}
return 0;
}