首页 > 其他分享 >[题目记录]P9999 [Ynoi2000] tmostnrq

[题目记录]P9999 [Ynoi2000] tmostnrq

时间：2025-01-12 16:59:54浏览次数：1  
标签：rt P9999 mn val tmostnrq int Ynoi2000 dep tag

P9999 [Ynoi2000] tmostnrq

题意

给定 \(n\) 个顶点的树，顶点编号为 \(1,\dots,n\)，给定长度 \(n_0\) 的序列 \(a_1,\dots,a_{n_0}\)，共 \(m\) 次查询，每次查询给定 \(l,r,x\)，问树的顶点 \(x\)，依次向 \(a_l,\dots,a_r\) 移动一步，到达的顶点。

若 \(x=y\)，则从顶点 \(x\) 向 \(y\) 移动一步到达 \(x\)，否则到达与 \(x\) 在树上相邻且距离 \(y\) 最近的位置。

$ n,m\le 1e6 $ , 时限 \(12 \mathrm s\) .

题解

发现移动过程不能简单地维护 , 考虑把一次移动看成一个函数 , 这就变成了一个函数复合问题 , 考虑离线用 lxl 讲的插入-标记-回收解决 .

考虑如何处理移动的过程 , 发现向 \(x\) 移动一位相当于把从 \(x\) 到根的路径全沿这条路径下移 , 其他点都上移 , 大概如图 :

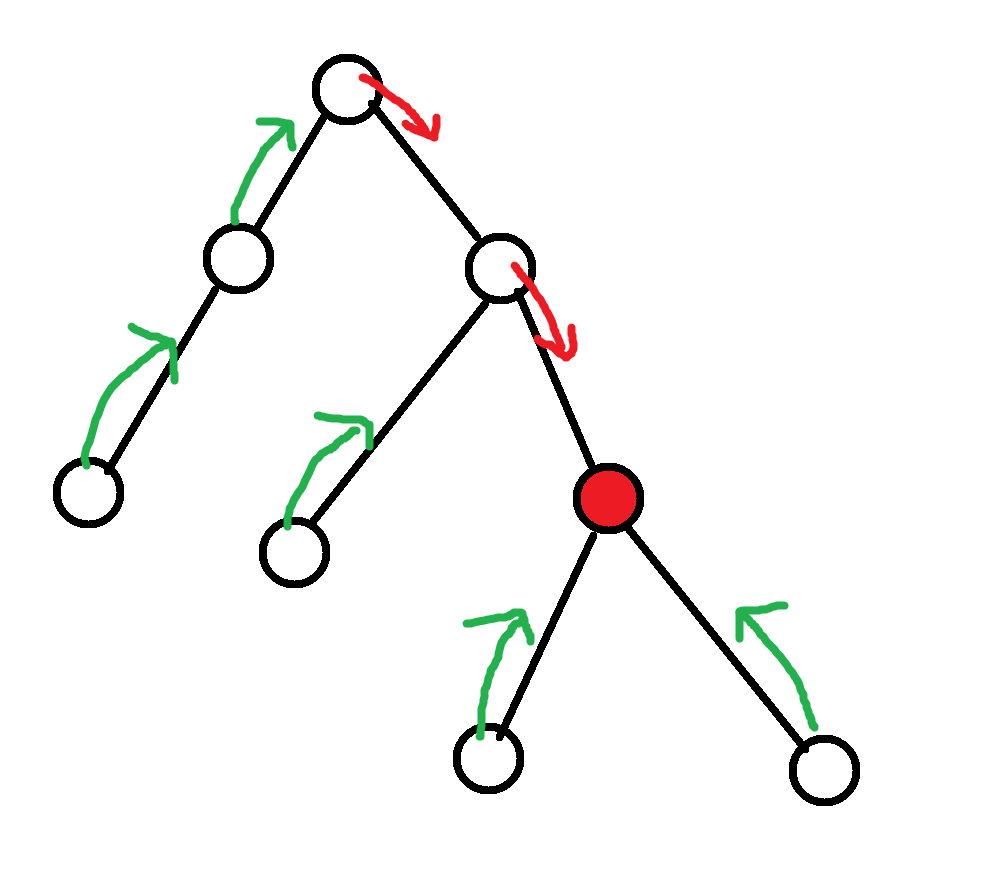
处理链的问题 , 就使用树链剖分 , 每次把向下跳的这条链单独处理 , 其余的向上跳打全局标记 .

对于每一条链 , 用以深度为关键字的 FHQ treap 维护 , 每次插入一个点 , 就直接把它插入到对应的链上 .

问题的关键是每一次移动的维护 :

每次处理链时 , 设向这条链上的 \(u\) 移动 , 相当于把平衡树分为 \(<dep_u\) 和 \(>dep_u\) 两部分 , 左边深度 \(+1\) , 右边深度 \(-1\) , 再合并起来 . 这样操作的总复杂度是 \(O(n\log^2 n)\) .

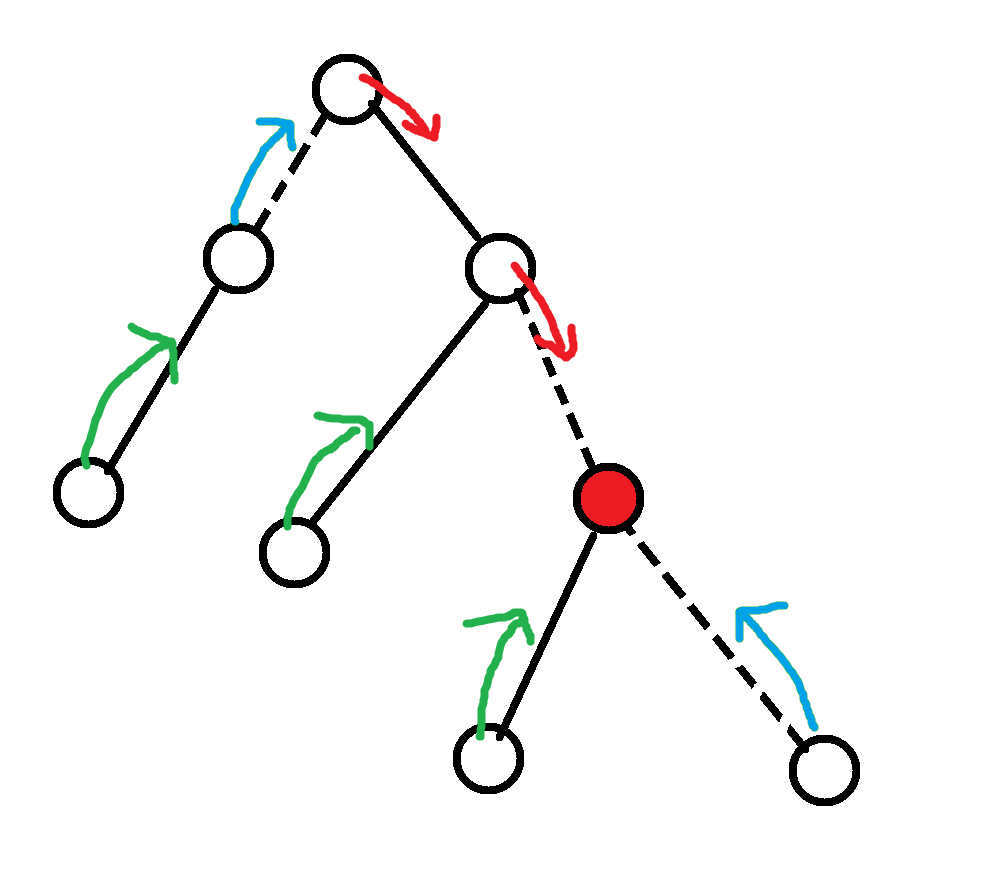
但是发现跳的过程中会出现一个点跳到了不同链上的情况 :

  • 第一种 : 设向这条链上的 \(u\) 移动 , 但 \(u\) 不是最初的起点 \(a_i\) , 这时 \(u\) 要通过向 \(a_i\) 方向移动的虚边跳到后一个链上 .

    因此如果 \(u\) 处有点 , 就把直接它插入到上一条链中 .

  • 第二种 : 如图中蓝边 , 打全局上移标记时 , 原来就在链顶的点会通过虚边上移 .

    因此每次操作后需要找到所有出现这种问题的链 , 把它的链顶点删掉插入到它的父亲所在链中 .

处理第二种的方法看起来十分暴力 , 但是稍加分析 , 每个点只有在通过虚边切换时会有额外复杂度 , 如果不考虑下移 , 每个点的切换次数是 $O(\log n) $ 次的 .

而考虑下移 , 每次操作也最多把 $ O(\log n) $ 个点通过虚边下移 , 相当于每次操作使后面多了 \(O(\log n)\) 次上移 . 也就是说 , 视每个点还能向上到根的次数为它的势能 , 总势能是 $O(n\log n+m\log n) $ 的 , 每消除一势能的复杂度是 $O(\log n) $ 的 , 所以这部分复杂度也是 \(O(n\log^2 n)\) , 最终复杂度就是 $O(n\log ^2 n) $ .

为了保证均摊部分的复杂度以及打整体标签的正确性 , 操作的实现都要足够精细 :

  • 如果两个点的位置重合 , 需要用并查集把他们并在一起 , 始终保证同一位置最多只有一个点 .

    否则 , 就无法保证跨虚边下移时 , 每一条虚边只有一个点下移 , 也就无法保证复杂度 .

  • 每次整体打上移标签 , 相当于让深度整体 \(-1\) , 但是我们手动调整的链部分是不能受它影响的 , 所以除了整体标记 \(tottag\) 要对每条链单独维护一个标记 \(tag_i\) . 设平衡树里记录的深度是 \(val\) , 它的深度真实值就应该是 \(val+tottag+tag_i\) .

    这样每次打标签的操作就是 \(tottag--\) , 然后所有从 \(x\) 到 \(1\) 经过的链 \(tag_i++\) .

    此外 , 为了方便操作 , 可以在对平衡树操作前更新 \(val\gets val+tottag+tag_i , tag_i\gets tottag\) .

  • 每次处理上移操作不能遍历所有链判断链顶是否有点 , 正确的做法是维护链中深度最小的点到顶的距离 . 设平衡树上深度最小值为 \(mn\) , 根据我们刚才的定义 , 它到顶的距离是 \(mn+tottag+tag_i-dep_{top}\) , 需要操作的链 , 满足 :

    \[mn+tottag+tag_i<dep_{top} \\ mn+tag_i-dep_{top}<-tottag \]

    可以用 set 维护所有链的 \(mn+tag_i-dep_{top}\) , 每次对平衡树操作时在 set 中更新对应的值 . 处理上移操作时直接取出 \(<-tottag\) 的链进行操作即可 .

  • 注意打标签的时机 , 操作时相当于先手动操作了所有在路径上的链 , 然后对它们 \(tag_i++\) 用来抵消整体 \(tottag\) , 不要一边操作一边动 \(tag\) , 否则可能导致从后面的链下移过来的点位置出错 .

  • 查询时可以直接记录对应的平衡树节点编号 ( 注意要取并查集的根 ) , 注意要把这个节点在平衡树上的祖先链都 pushdown , 还要考虑链上的 \(tag\) , 这样就可以取出它的深度 , 结合所在的重链就可以取出具体位置 .

点击查看代码 
#include<bits/stdc++.h>
#define file(x) freopen(#x ".in","r",stdin),freopen(#x ".out","w",stdout)
#define ll long long
using namespace std;

constexpr int N=1e6+5;
constexpr int INF=1e7;

struct node{
	int ls,rs,rnd,fa,val,tag;
}a[N];
int at;

inline int add(int dep){
	a[++at]={0,0,rand(),0,dep,0};
	return at;
}

inline void pushdown(int x){
	a[a[x].ls].val+=a[x].tag;
	a[a[x].ls].tag+=a[x].tag;
	a[a[x].rs].val+=a[x].tag;
	a[a[x].rs].tag+=a[x].tag;
	a[x].tag=0;
}

inline void pushup(int x){
	if(a[x].ls) a[a[x].ls].fa=x;
	if(a[x].rs) a[a[x].rs].fa=x;
	a[x].fa=0;
}

void split(int u,int k,int &x,int &y){
	if(!u) {
		x=y=0;return;
	}
	pushdown(u);
	if(a[u].val<=k){
		x=u;
		split(a[u].rs,k,a[x].rs,y);
		pushup(x);
	}
	else{
		y=u;
		split(a[u].ls,k,x,a[y].ls);
		pushup(y);
	}
}

int merge(int x,int y){
	if(x==0||y==0) return x+y;
	pushdown(x);pushdown(y);
	if(a[x].rnd<=a[y].rnd){
		a[x].rs=merge(a[x].rs,y);
		pushup(x);
		return x;
	}
	else{
		a[y].ls=merge(x,a[y].ls);
		pushup(y);
		return y;
	}
	return 0;
}

int get(int x,int k){
	if(!x) return 0;
	pushdown(x);
	if(a[x].val>k) return get(a[x].ls,k);
	if(a[x].val<k) return get(a[x].rs,k);
	return x;
}

int getmin(int x){
	if(!x) return INF;
	pushdown(x);
	if(a[x].ls) return getmin(a[x].ls);
	return a[x].val;
}

int fd[N];
int find(int x){
	if(x==fd[x]) return x;
	fd[x]=find(fd[x]);
	return fd[x];
}


int n,tn,m,to[N];

vector<int> e[N];

vector<pair<int,int> > inp[N];
vector<int> oup[N];
int nump[N],res[N];

int fa[N],dep[N],son[N],sz[N],top[N],dfn[N],rnk[N],L[N],R[N],rt[N],tot,pos[N];

int ft[N][24];

void dfs1(int u){
	ft[u][0]=fa[u];
	for(int i=1;i<=20;i++)
		ft[u][i]=ft[ft[u][i-1]][i-1];

	sz[u]=1;
	for(auto v:e[u]){
		if(v==fa[u]) continue;
		fa[v]=u;dep[v]=dep[u]+1;
		dfs1(v);
		sz[u]+=sz[v];
		if(sz[v]>sz[son[u]]) son[u]=v;
	}
}

int tottag,tag[N],mn[N];
set<pair<int,int> > st;

void dfs2(int u,int t){
	dfn[u]=++tot;rnk[tot]=u;
	top[u]=t;
	if(u==t){
		L[t]=u;
		mn[t]=INF;tag[t]=0;
		st.insert({INF-dep[t],t});
	}
	R[t]=u;
	if(son[u])
		dfs2(son[u],t);
	for(auto v:e[u])
		if(v!=fa[u]&&v!=son[u])
			dfs2(v,v);
}


inline void pushtag(int t){
	int tg=tottag+tag[t];
	a[rt[t]].val+=tg,a[rt[t]].tag+=tg;
	mn[t]+=tg;
	tag[t]=-tottag;
}

inline void insert(int x,int t){
	if(!x) return;
	int d=a[x].val;
	pushtag(t);
	int link=get(rt[t],d);
	if(link) fd[x]=link;
	else{
		st.erase({mn[t]+tag[t]-dep[t],t});
		int u,v;split(rt[t],d,u,v);
		rt[t]=merge(u,merge(x,v));
		pos[rt[t]]=t;
		mn[t]=getmin(rt[t]);
		st.insert({mn[t]+tag[t]-dep[t],t});
	}
}


inline void solve(int x){
	int u,v,w,y,z,tmp,t;
	pushtag(top[x]);
	split(rt[top[x]],dep[x]-2,u,tmp);
	split(tmp,dep[x]+1,v,z);tmp=v;
	split(tmp,dep[x]-1,v,y);tmp=y;
	split(tmp,dep[x],w,y);
	
	a[v].val++;a[v].tag++;a[y].val--;a[y].tag--;
	if(v&&w) fd[v]=w,v=0;
	if(y&&w) fd[y]=w,y=0;
	if(v&&y) fd[v]=y,v=0;
	a[u].val++;a[u].tag++;a[z].val--;a[z].tag--;
	rt[top[x]]=merge(u,merge(v+w+y,z));
	pos[rt[top[x]]]=top[x];


	int last=x;
	while(top[x]!=1){
		last=x;
		x=fa[top[x]];

		pushtag(top[x]);
		split(rt[top[x]],dep[x]-2,u,tmp);
		split(tmp,dep[x]+1,v,z);tmp=v;
		split(tmp,dep[x]-1,v,y);tmp=y;
		split(tmp,dep[x],w,y);
		

		t=top[last];
		st.erase({mn[t]+tag[t]-dep[t],t});
		if(w){
			a[w].val++,a[w].tag++;
			int d=a[w].val;
			int link=get(rt[t],d);
			if(link) fd[w]=link;
			else rt[t]=merge(w,rt[t]);
			pos[rt[t]]=t;
		}
		tag[t]++;
		mn[t]=getmin(rt[t]);
		st.insert({mn[t]+tag[t]-dep[t],t});

		a[v].val++;a[v].tag++;a[y].val--;a[y].tag--;
		if(v&&y) fd[v]=y,v=0;

		a[u].val++;a[u].tag++;a[z].val--;a[z].tag--;
		rt[top[x]]=merge(u,merge(v+y,z));
		pos[rt[top[x]]]=top[x];

	}
	t=top[x];
	st.erase({mn[t]+tag[t]-dep[t],t});
	tag[t]++;
	mn[t]=getmin(rt[t]);
	st.insert({mn[t]+tag[t]-dep[t],t});

	tottag--;
	vector<int> d;d.clear();
	for(auto x:st){
		if(x.first>=-tottag) break;
		d.push_back(x.second);
	}
	for(auto t:d){
		pushtag(t);
		st.erase({mn[t]+tag[t]-dep[t],t});
		split(rt[t],dep[t]-1,u,v);
		rt[t]=v;pos[v]=t;
		mn[t]=getmin(rt[t]);
		st.insert({mn[t]+tag[t]-dep[t],t});

		insert(u,top[fa[t]]);
	}
}

inline int query_pos(int u,int d){
	for(int i=20;i>=0;i--)
		if(dep[ft[u][i]]>=d) u=ft[u][i];
	return u;
}

int q[N],tp;

inline int query(int x){
	tp=0;q[++tp]=x;
	while(a[x].fa) q[++tp]=a[x].fa,x=a[x].fa;
	int st=R[pos[q[tp]]];
	pushtag(pos[q[tp]]);
	while(tp) pushdown(q[tp--]);
	return query_pos(st,a[q[1]].val);
}

namespace debug{

	int s;
	int tres[N],fa[N];

	void dfs(int u){
		for(auto v:e[u]){
			if(v==fa[u]) continue;
			fa[v]=u; dfs(v);
		}
	}

	int solve(int l,int r,int x){
		for(int i=l;i<=r;i++){
			fa[to[i]]=to[i];
			dfs(to[i]);
			x=fa[x];
		}
		return x;
	}
	void init(){
		cin>>s;srand(s);
		n=15;tn=10;m=10;
		cout<<n<<' '<<tn<<' '<<m<<'\n';
		for(int i=2;i<=n;i++){
			int tmpf=rand()%(i-1)+1;
			cout<<tmpf<<' ';
			e[tmpf].push_back(i);
			e[i].push_back(tmpf);
		}
		cout<<'\n';
		for(int i=1;i<=tn;i++){
			to[i]=rand()%n+1;
			cout<<to[i]<<' ';
		}
		cout<<'\n';
		for(int i=1;i<=m;i++) {
			int l=rand()%tn+1,r=rand()%tn+1,x=rand()%n+1;
			if(l>r) swap(l,r);
			cout<<l<<' '<<r<<' '<<x<<'\n';
			inp[l].push_back({i,x});
			oup[r].push_back(i);
			tres[i]=solve(l,r,x);
		}
	}
	void check(){
		for(int i=1;i<=m;i++){
			if(res[i]!=tres[i]){
				cout<<"WA! pos:"<<i<<" answer="<<tres[i];
				return;
			}
		}
		cout<<"AC!";
	}
}

void input(){
	cin>>n>>tn>>m;
	for(int i=2;i<=n;i++) {
		int u,v;cin>>u;v=i;
		e[u].push_back(v);
		e[v].push_back(u);
	}
	for(int i=1;i<=tn;i++) cin>>to[i];
	for(int i=1;i<=m;i++){
		int l,r,x;cin>>l>>r>>x;
		inp[l].push_back({i,x});
		oup[r].push_back(i);
	}
}

int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);

	//debug::init();
	input();

	dep[1]=1;dfs1(1);dfs2(1,1);
	for(int i=1;i<=m;i++) fd[i]=i;
	for(int i=1;i<=tn;i++){
		for(auto [id,u]:inp[i]){
			int now=add(dep[u]);
			insert(now,top[u]);
			nump[id]=now;
		}
		solve(to[i]);
		for(auto id:oup[i]){
			res[id]=query(find(nump[id]));
		}
	}
	for(int i=1;i<=m;i++) cout<<res[i]<<'\n';

	//debug::check();

}

总结

结合 lxl 讲的这一类问题的套路 , 这道题的思路其实还是很清晰的 . 甚至看起来细节都不是特别繁琐 .

然而实现起来还是非常难写 , 因为维护的是深度 , 还有全局打 tag , 合并相同点的问题 , 导致所有操作都没有看起来那么直接 .

因为以下问题调了 14h+ :

  • 打标签时机出错 .

  • 并查集预处理要 \(m\) 个而非 \(n\) 个.

  • pushup(y) 写成 pushup(x) .

  • 合并点少考虑情况 .

  • 查询时没有考虑全局 tag

其中最后一个问题卡了一个上午加一个下午 . 手搓数据全都没看出问题 , 最后是靠对拍拍出了问题 . 所以在真的找不出问题时还是对拍比较有效 .

不管怎么说终于调出来这道题了 .

标签：rt,P9999,mn,val,tmostnrq,int,Ynoi2000,dep,tag
From： https://www.cnblogs.com/youlv/p/18667075

相关文章

  • [Ynoi2000] tmostnrq 做题记录
    link先离线扫描线，相当于在\(l\)这个时刻加入一个点，然后每次令所有点向某个点的方向移动一步，在\(r\)时刻查询某个点的位置。以\(1\)为根，对于\(a_i\)相当于令\(1\toa_i\)这条链上所有点向下移动一步，其他点向上移动一步。我们需要同时支持这两种操作，但是不能每个点暴力......
  • P9999 [Ynoi2000] tmostnrq 题解
    巨大难写题。就这样一个毒瘤的题，还有人把时空缩小成二分之一放在模拟赛，太好笑了。思路首先将询问离线。我们在\(l_i\)处加入这个点，在\(r_i\)处查询这个点在哪里。那么我们就需要有一个数据结构支持让所有树上的节点一起动。考虑所有点往\(x\)处动。那么对于在\(1\si......
  • P9997 [Ynoi2000] pmpkmp
    我永远喜欢数据结构。lxl大毒瘤！开写到AC耗时\(5\)天的大毒瘤题，期间学习了神仙@云浅知处的思路。他修改部分的代码也帮助我找到锅AC，膜拜云浅！本题是CF1045JMoonwalkchallenge的加强版，码量超过\(6\text{KB}\)，作为一名对读者负责人的笔者，我在此必须郑重警告：\[\color{re......
  • [Ynoi2000] pri
    问题等价于区间翻转区间顺序对数，显然没有复杂度比较好的做法。将操作序列每\(B\)个分一组，对每组进行处理。\(B\)个操作会将序列划分为\(B\)个连续段，在每次操作后都是连续段的一个排列，以及每个连续段内部可能翻转。我们称每个连续段为一个等价类。将值域按\(C\)大小分块......
  • P9995 [Ynoi2000] rspcn 题解
    思路比较典的ODT题目。发现排序是一个非常有性质的操作。它对区间的更改与颜色段均摊差不多。那么我们可以想到用ODT来维护这一整个序列。具体的，区间排序操作可以用ODT维护每次排序产生的段，每段用线段树维护排序后的结果。每次修改就可以进行线段树的分裂与合并。如......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99