一、栈
栈(stack)是一种操作受限的线性表数据结构,基于后进先出(LIFO)策略的集合类型,例如函数中的临时变量符合后进先出的特性,因此用栈保存最合适。
在入栈和出栈过程中所需的空间复杂度是 O(1),时间复杂度也是 O(1)。空间复杂度是指运行算法还需要的额外存储空间。
注意,内存中的堆栈和数据结构中的堆栈不是一个概念,前者是真实存在的物理区,后者是抽象的数据存储结构。
面试题30包含min函数的栈。在压栈时,与之前的最小值比较,每次把两者较小的那个值存放到辅助栈中。
面试题31栈的压入和弹出序列。如果弹出的数字是栈顶,则弹出;如果弹出的数字不在栈顶,则把还没入栈的数字压入到辅助栈中,直到栈顶是弹出数字为止。
1)括号匹配
用正确的类型和顺序匹配括号,例如“(”跟“)”匹配,“[”跟“]”匹配,“{”跟“}”匹配。例题:LeetCode的20. 有效的括号。
第一种思路是,当遇到匹配的最小括号对时,将它们从栈中删除(即出栈),如果最后栈为空,那么它是有效的括号,反之不是,代码如下所示。
function isValidParentheses(s) {
const length = s.length;
let i = 0;
const stack = [];
while (i < length) {
let stackLen = stack.length > 0 ? stack.length - 1 : stack.length;
if (
(stack[stackLen] == "(" && s[i] == ")") ||
(stack[stackLen] == "{" && s[i] == "}") ||
(stack[stackLen] == "[" && s[i] == "]")
) {
stack.pop();
i++;
continue;
}
stack.push(s[i]);
i++;
}
return stack.length === 0;
}
第二种思路是巧妙的利用一张映射表,以右括号为键,左括号为值。先判断当前字符是否是左括号,若是,就入栈,否则匹配当前栈顶元素是否与当前字符匹配。
function isValidParentheses(s) {
const stack = [],
map = { "}": "{", "]": "[", ")": "(" };
for (let i = 0, len = s.length; i < len; i++) {
let c = s[i];
if (!map[c]) {
stack.push(c);
continue;
}
if (stack.length > 0 && map[c] != stack.pop())
return false;
}
return stack.length == 0;
}
2)算术表达式求值
( 1 + ( 2 + 3 ) * ( 4 * 5 ) ) 是一个算术表达式,如果将4乘以5,把3加上2,取它们的积然后加1,就得到了101。
表达式由括号、运算符和操作数(数字)组成,可以用两个栈分别保存运算符和操作数来完成算术求值,处理过程如下所列。
(1)将操作数压入操作数栈;
(2)将运算符压入运算符栈;
(3)忽略左括号;
(4)在遇到右括号时,弹出一个运算符,弹出所需数量的操作数,并将运算符和操作数的运算结果压入操作数栈。
源码如下所示。例题:LeetCode的150. 逆波兰表达式求值。
function evalExpress(s) {
const length = s.length;
let i = 0;
const ops = [],
vals = [];
while (i < length) {
let word = s[i];
if (word == "(") {
} else if (word == "+" || word == "-" || word == "*" || word == "/")
ops.push(word);
else if (word == ")") {
let op = ops.pop(),
val = vals.pop();
if (op == "+") val = vals.pop() + val;
else if (op == "-") val = vals.pop() - val;
else if (op == "*") val = vals.pop() * val;
else if (op == "/") val = vals.pop() / val;
vals.push(val);
} else
vals.push(parseInt(word));
i++;
}
return vals.pop();
}
二、队列
队列(queue)也是一种操作受限的线性表数据结构,基于先进先出(FIFO)策略的集合类型,队列的应用非常广泛,例如循环队列、阻塞队列、并发队列等。
栈只需一个栈顶指针,而队列需要两个:队首指针和队尾指针。
面试题9用两个栈实现队列。先进后出的栈实现先进先出的队列,一系列栈的压入和弹出模拟队列。
面试题59窗口滑动的最大值。只把可能成为滑动窗口最大值的数存入一个两端开口的队列(deque)。延伸题:队列的最大值。
1)循环队列
循环队列是首尾相连的队列,这样可避免在出队时进行数据搬移的操作,但需要准确的判断出队空和队满,如下所示。例题:LeetCode的641. 设计循环双端队列。
class CircularQueue {
constructor(capacity) {
this.items = [];
this.n = capacity; //队列大小
this.head = 0; //队首指针
this.tail = 0; //队尾指针
}
enqueue(item) {
const { head, tail, n } = this;
//队满
if ((tail + 1) % n == head) return false;
this.items[tail] = item;
//队尾没有存储数据,会浪费一个数组的存储空间
this.tail = (tail + 1) % n;
return true;
}
dequeue() {
const { head, tail, n, items } = this;
//队空
if (head == tail) return null;
const result = items[head];
this.head = (head + 1) % n;
return result;
}
}
leetcode题精选
栈
[20] 有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。示例 1:
输入:s = "()"
输出:true
示例 2:输入:s = "()[]{}"
输出:true
示例 3:输入:s = "(]"
输出:false
示例 4:输入:s = "([)]"
输出:false
示例 5:输入:s = "{[]}"
输出:true
由于栈结构的特殊性,非常适合做对称匹配类的题目。
首先要弄清楚,字符串里的括号不匹配有几种情况。
一些同学,在面试中看到这种题目上来就开始写代码,然后就越写越乱。
建议要写代码之前要分析好有哪几种不匹配的情况,如果不动手之前分析好,写出的代码也会有很多问题。
先来分析一下 这里有三种不匹配的情况,
第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
第二种情况,括号没有多余,但是 括号的类型没有匹配上。
第三种情况,字符串里右方向的括号多余了,所以不匹配。
我们的代码只要覆盖了这三种不匹配的情况,就不会出问题,可以看出 动手之前分析好题目的重要性。
动画如下:
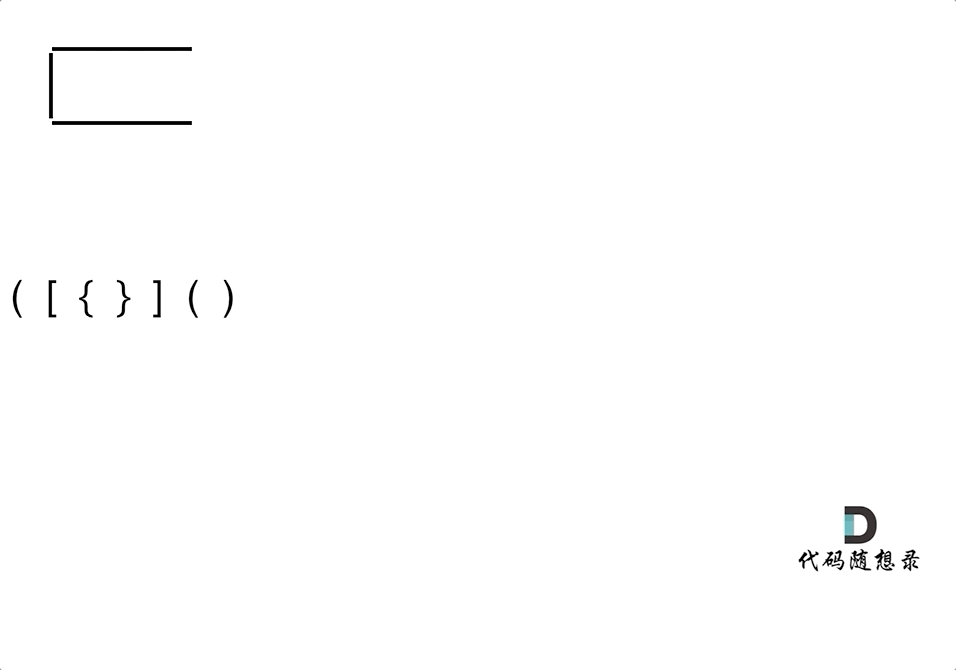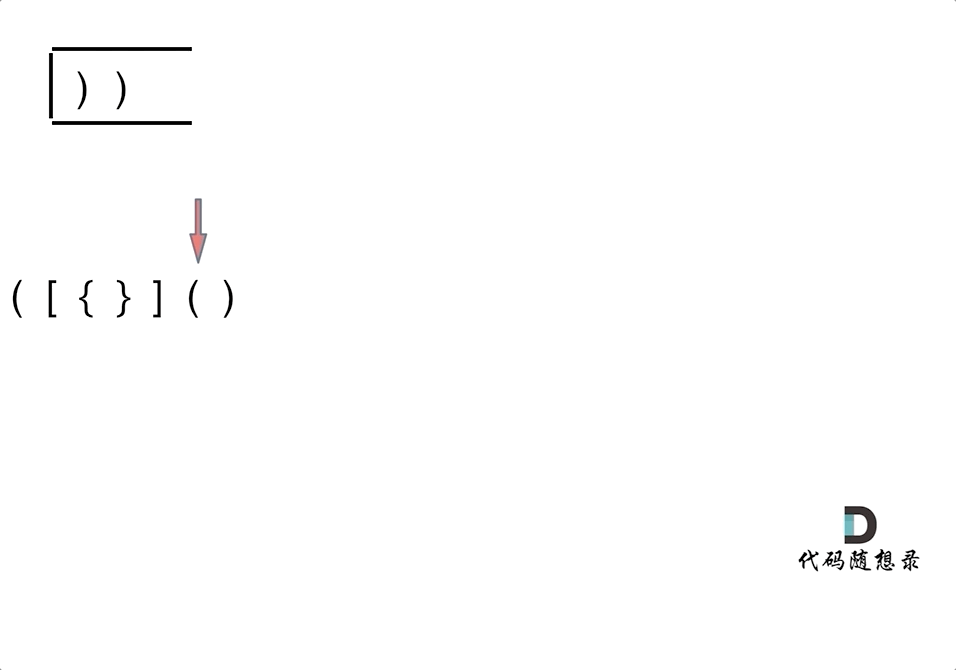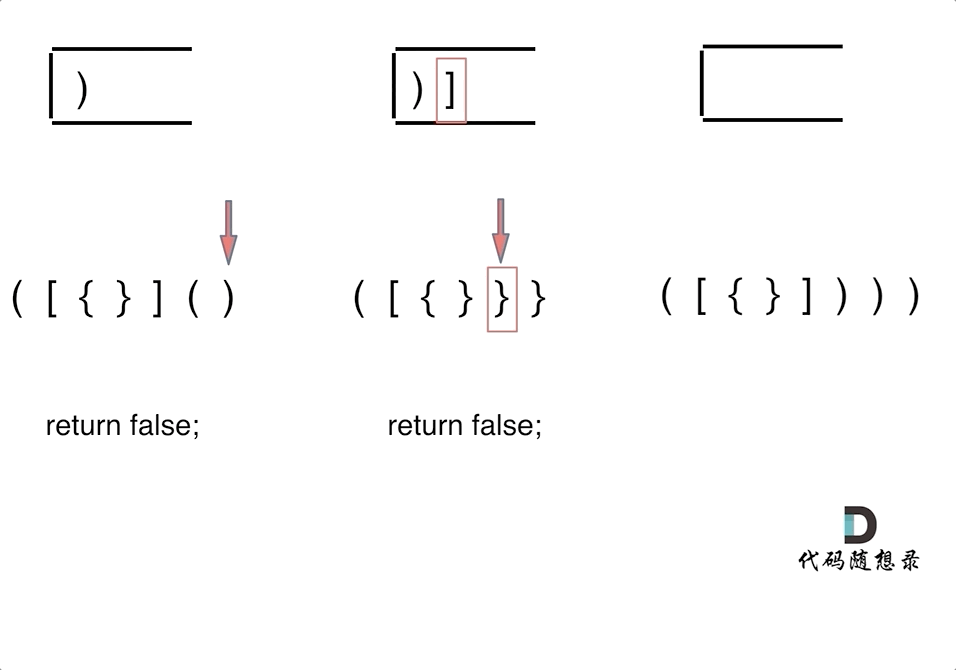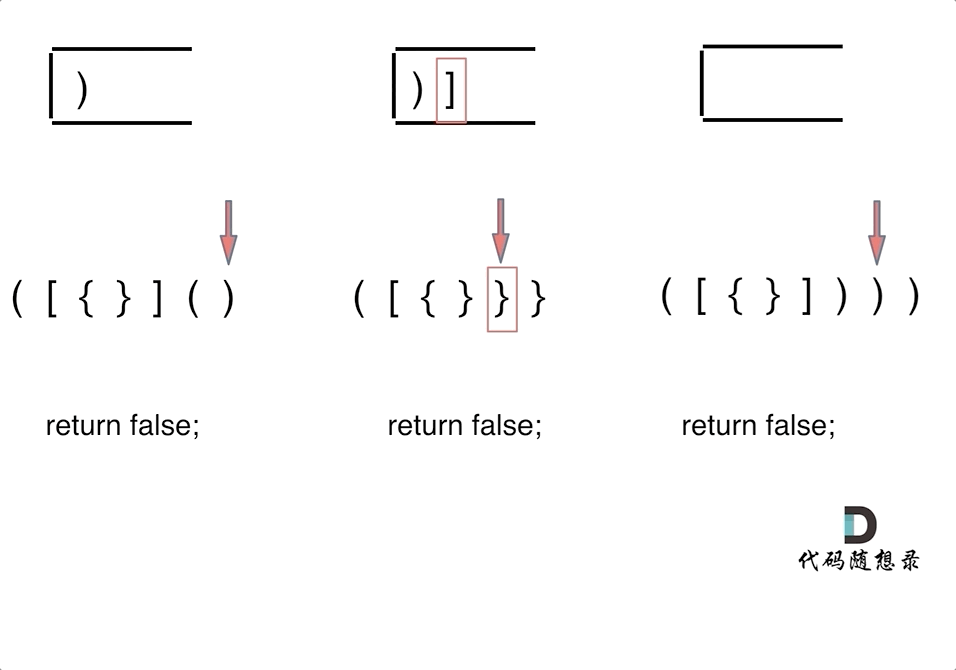
第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
第二种情况:遍历字符串匹配的过程中,发现栈里没有要匹配的字符。所以return false
第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号return false
那么什么时候说明左括号和右括号全都匹配了呢,就是字符串遍历完之后,栈是空的,就说明全都匹配了。
分析完之后,代码其实就比较好写了,
但还有一些技巧,在匹配左括号的时候,右括号先入栈,就只需要比较当前元素和栈顶相不相等就可以了,比左括号先入栈代码实现要简单的多了!
function isValid(s: string): boolean {
let stack :string[] = [];
//进行遍历
for(let i = 0; i < s.length ; i++ ){
let x:string = s[i];
switch (x) {
//若是左括号则入栈
case '(' :
stack.push(')');
break;
case '[' :
stack.push(']');
break;
case '{' :
stack.push('}');
break;
//否则出栈 看是否匹配
default:
if(stack.pop() !== x) return false;
break;
}
}
//看是否有多余的未匹配的
return stack.length === 0;
};
//版本二:优化版 哈希表 左括号作为属性 右括号作为zhi
function isValid(s: string): boolean {
type BracketMap = {
[index: string]: string;
}
let helperStack: string[] = [];
let bracketMap: BracketMap = {
'(': ')',
'[': ']',
'{': '}'
}
for (let i of s) {
if (bracketMap.hasOwnProperty(i)) {
helperStack.push(bracketMap[i]);
} else if (i !== helperStack.pop()) {
return false;
}
}
return helperStack.length === 0;
};
[155] 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。示例 1:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]输出:
[null,null,null,null,-3,null,0,-2]解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
单栈解法
class MinStack {
stack: Array<number>;// 维护一个数组做stack
min: number; // 维护一个min
constructor() {
this.stack = [];
this.min = Infinity;
}
push(x: number): void {
// push进来 除了放进来 还要比较是否最小 最小换掉min
this.stack.push(x);
if (x < this.min) this.min = x;
}
pop(): void {
// pop出去 除了pop出去 无脑直接重新确定一下min
this.stack.pop();
this.min = Math.min(...this.stack);
}
top(): number {
// 就是stack最后有个数咯 no doubt
return this.stack[this.stack.length - 1];
}
getMin(): number {
// 返回min完事
return this.min;
}
}
双栈解法:
问题分析
新建一个最小栈,每次push元素时,将当前栈的最小值放入最小栈中。即栈顶始终存放着该栈内元素最小值。
解题思路
建两个栈,一个正常的栈,一个最小栈存放当前栈最小值
push元素时,由于栈顶保存的永远是最小值,所以当入栈时只需要比较入栈值与最小栈栈顶值即可得出最小值,将最小值存入最小栈中。
保持两个栈同步操作,出栈时也同步出栈。
复杂度分析
push、pop、top、getMin时间复杂度均为O(1)
空间复杂度O(n)
class MinStack {
protected Stack:number[] = [];
protected MinStack:number[] = [];
push(val: number): void {
this.Stack.push(val);
this.MinStack.push(Math.min(val, this.getMin() ?? Infinity));
}
pop(): void {
this.Stack.pop();
this.MinStack.pop();
}
top(): number {
return this.Stack[this.Stack.length - 1];
}
getMin(): number {
return this.MinStack[this.MinStack.length - 1];
}
}
[225] 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。注意:
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。示例:
输入:
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false]解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
一个队列实现
- 解题思路
push操作时先记录下当前队列长度n,然后将元素x入队,再将队列元素依次出队,入队n次,这样队首元素就是新入队元素x。
时间复杂度:入栈操作 O(n),其余操作都是 O(1)。
空间复杂度:O(n),其中 n 是栈内的元素。需要使用一个队列存储栈内的元素。
class MyStack {
queue: number[] = [];
push(x: number): void {
let n = this.queue.length;
this.queue.push(x);
for (let i = 0; i < n; i++) {
this.queue.push(this.queue.shift());
}
}
pop(): number {
return this.queue.shift();
}
top(): number {
return this.queue[0];
}
empty(): boolean {
return this.queue.length == 0;
}
}
两个队列实现
设置两个队列queue1、queue2, 把每次push的元素放入queue2中,然后再将queue1队列出队,依次放入queue2中,这样新入队元素就排在了queue2的队首,最后我们将queue1和queue2交换。
时间复杂度:入栈操作 O(n),其余操作都是 O(1)。
入栈操作需要将q1中的 n 个元素出队,并入队 n+1 个元素到 q2,共有 2n+1 次操作,所以入栈操作的时间复杂度是 O(n)。
空间复杂度:O(n),其中 n 是栈内的元素。需要使用两个队列存储栈内的元素
class MyStack {
queue1: number[] = [];
queue2: number[] = [];
push(x: number): void {
this.queue2.push(x);
while (this.queue1.length) {
this.queue2.push(this.queue1.shift());
}
this.queue1 = this.queue2;
this.queue2 = [];
}
pop(): number {
return this.queue1.shift();
}
top(): number {
return this.queue1[0];
}
empty(): boolean {
return this.queue1.length === 0;
}
}
[232] 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。示例 1:
输入:
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false
双栈实现:
- 用stack1、stack2两个栈实现队列 stack后进先出 myqueue先进先出
- push方法将数据放到stack1中,stack1用来存储数据
- pop方法将stack2中的栈顶数据弹出去,当stack2空的时候,将stack1 pop出来,放入stack2中,这就实现了队列的效果
时间复杂度
- 老元素压入两次,弹出两次。新元素压入一次、弹出一次
- 4n+2次,n是队列大小
- 压入和弹出O(1),总的O(n)
空间复杂度 O(n)
class MyQueue {
stack1: Array<number>
stack2: Array<number>
constructor() {
// 用来入栈
this.stack1 = [];
// 用来出栈
this.stack2 = [];
}
push(x: number): void {
this.stack1.push(x);
}
pop(): number {
// 只要 stack2 有值,就直接 return
if (this.stack2.length > 0) {
return this.stack2.pop();
}
// 当 stack2为空的时候,将 stack1 的值放到 stack2 中
while (this.stack1.length > 0) {
this.stack2.push(this.stack1.pop());
}
return this.stack2.pop();
}
peek(): number {
let tmp = this.pop();
this.stack2.push(tmp);
return tmp;
}
empty(): boolean {
return this.stack1.length === 0 && this.stack2.length === 0;
}
}
[1047] 删除字符串中的所有相邻重复项
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
- 输入:"abbaca"
- 输出:"ca"
- 解释:例如,在 "abbaca" 中,我们可以删除 "bb" 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca",其中又只有 "aa" 可以执行重复项删除操作,所以最后的字符串为 "ca"。
单调栈
通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了。
时间复杂度为O(n)。
那么单调栈的原理是什么呢?为什么时间复杂度是O(n)就可以找到每一个元素的右边第一个比它大的元素位置呢?
单调栈的本质是空间换时间,因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素,优点是只需要遍历一次。
在使用单调栈的时候首先要明确如下几点:
- 单调栈里存放的元素是什么?
单调栈里只需要存放元素的下标i就可以了,如果需要使用对应的元素,直接T[i]就可以获取。
- 单调栈里元素是递增呢? 还是递减呢?
注意一下顺序为 从栈头到栈底的顺序,因为单纯的说从左到右或者从前到后,不说栈头朝哪个方向的话,大家一定会越看越懵。
这里我们要使用递增循序(再强调一下是指从栈头到栈底的顺序),因为只有递增的时候,加入一个元素i,才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i。
文字描述理解起来有点费劲,接下来我画了一系列的图,来讲解单调栈的工作过程。
使用单调栈主要有三个判断条件。
- 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
[739] 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:输入: temperatures = [30,60,90]
输出: [1,1,0]
我们用temperatures = [73, 74, 75, 71, 71, 72, 76, 73]为例来逐步分析,输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
首先先将第一个遍历元素加入单调栈 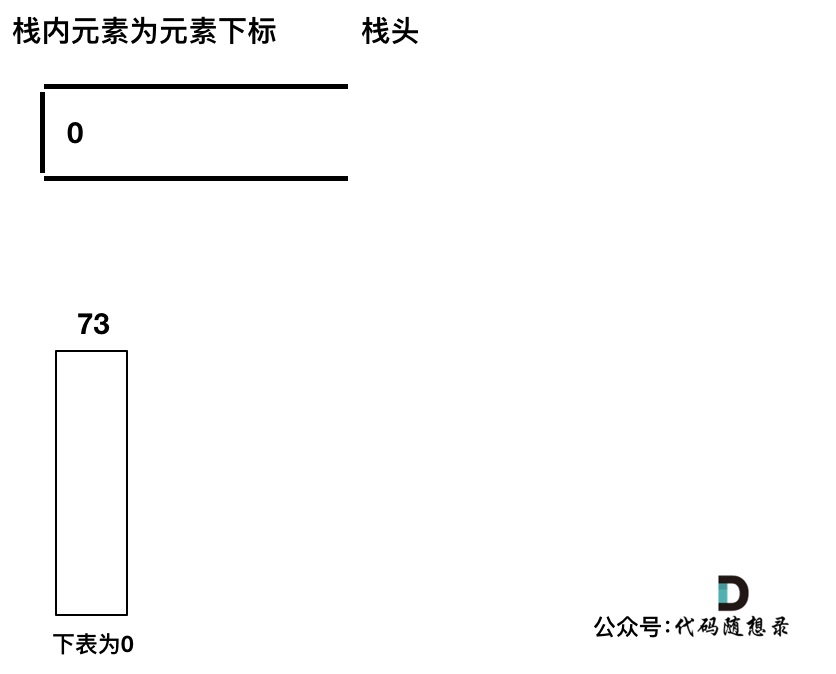
加入T[1] = 74,因为T[1] > T[0](当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),而我们要保持一个递增单调栈(从栈头到栈底),所以将T[0]弹出,T[1]加入,此时result数组可以记录了,result[0] = 1,即T[0]右面第一个比T[0]大的元素是T[1]。 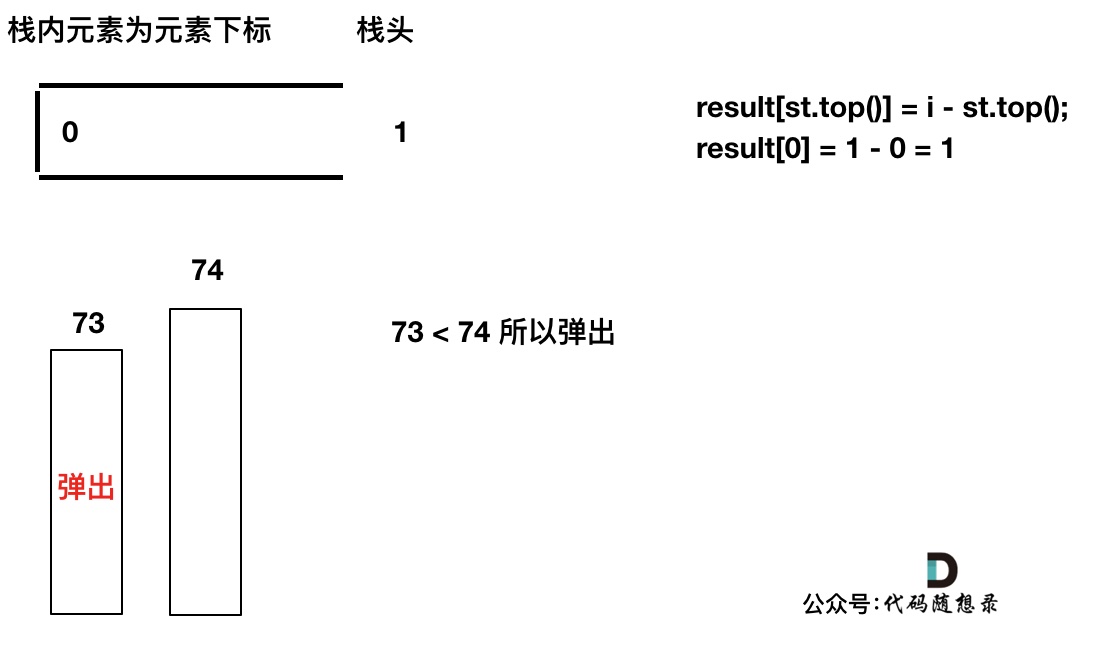
加入T[2],同理,T[1]弹出
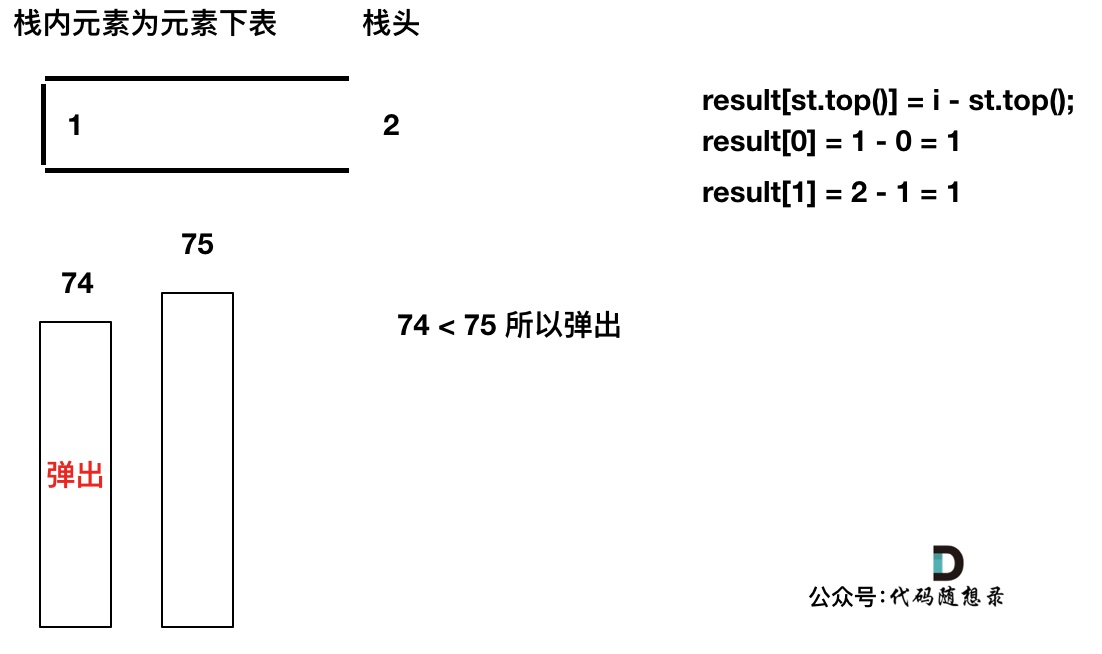
加入T[3],T[3] < T[2] (当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况),加T[3]加入单调栈。
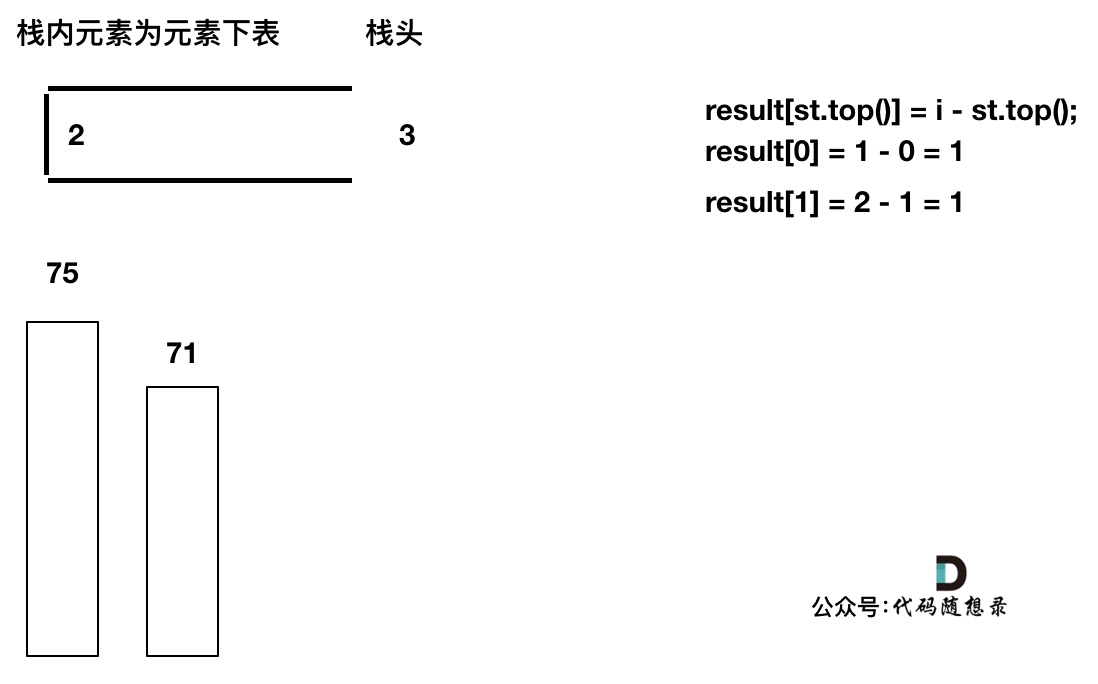
加入T[4],T[4] == T[3] (当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况),此时依然要加入栈,不用计算距离,因为我们要求的是右面第一个大于本元素的位置,而不是大于等于! 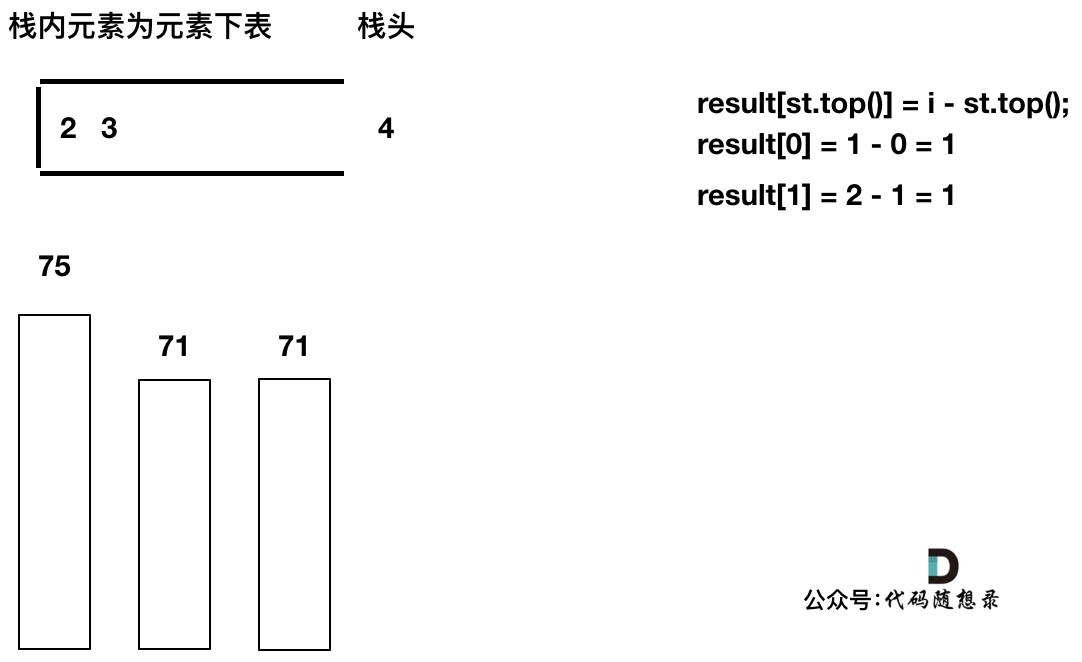
加入T[5],T[5] > T[4] (当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),将T[4]弹出,同时计算距离,更新result 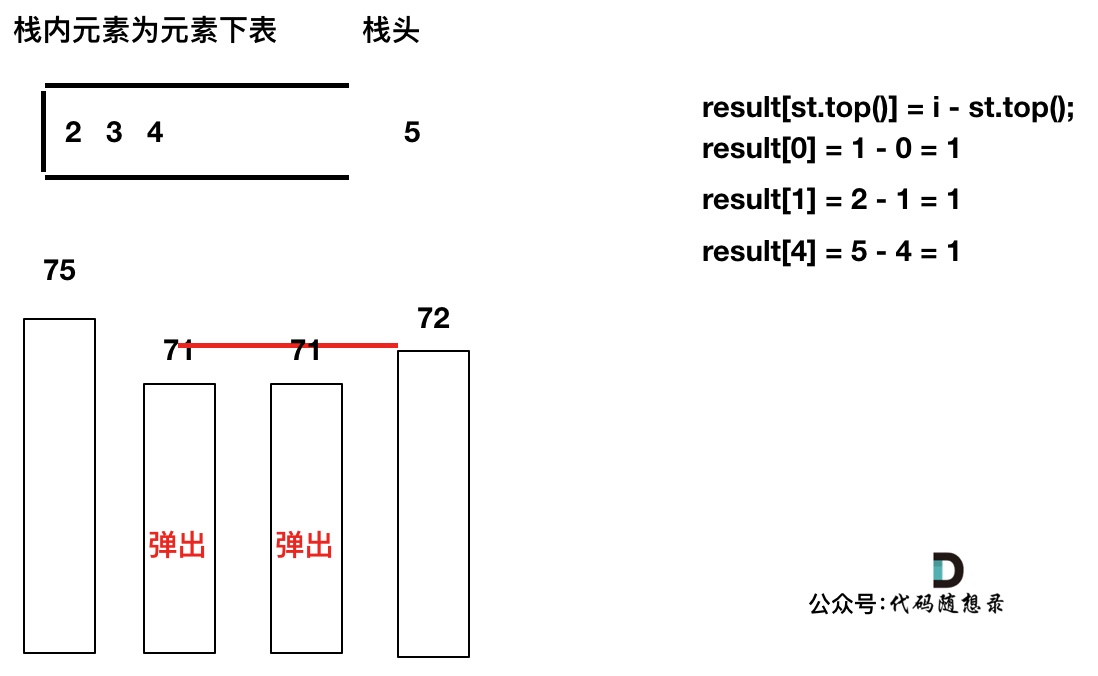
T[4]弹出之后, T[5] > T[3] (当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),将T[3]继续弹出,同时计算距离,更新result 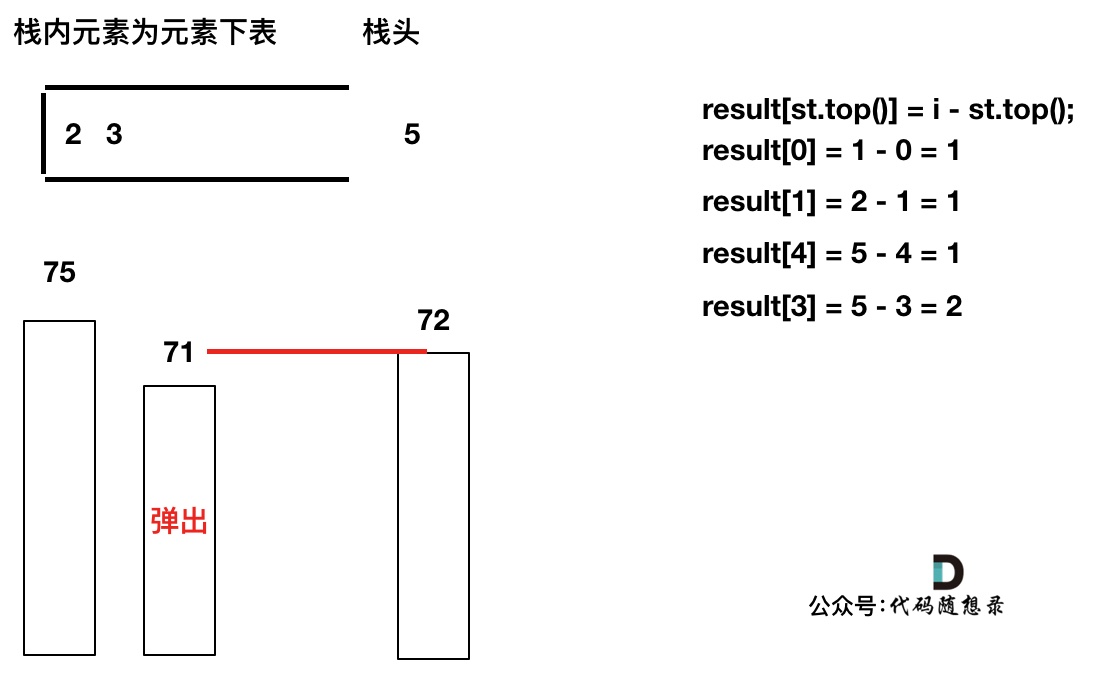
直到发现T[5]小于T[st.top()],终止弹出,将T[5]加入单调栈 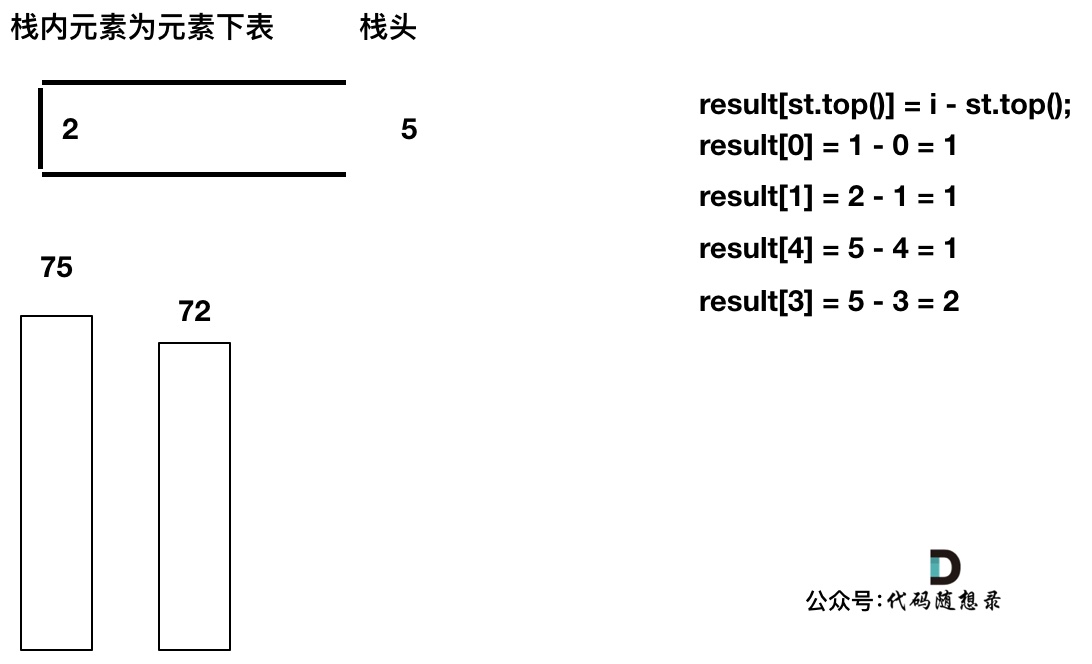
加入T[6],同理,需要将栈里的T[5],T[2]弹出 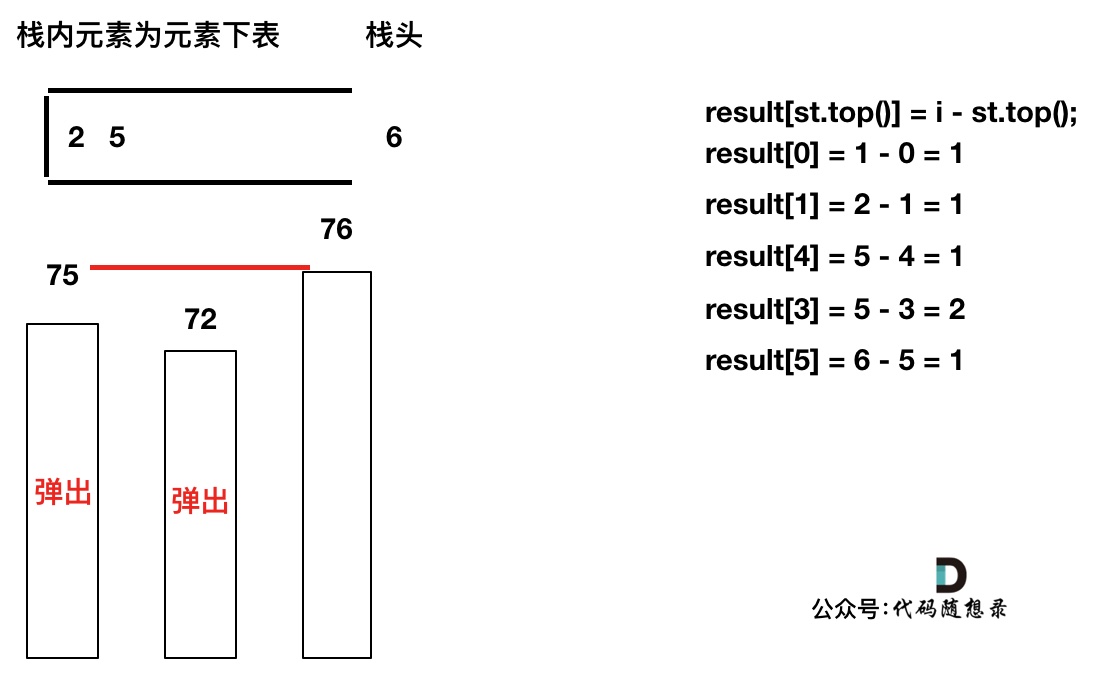
同理,继续弹出 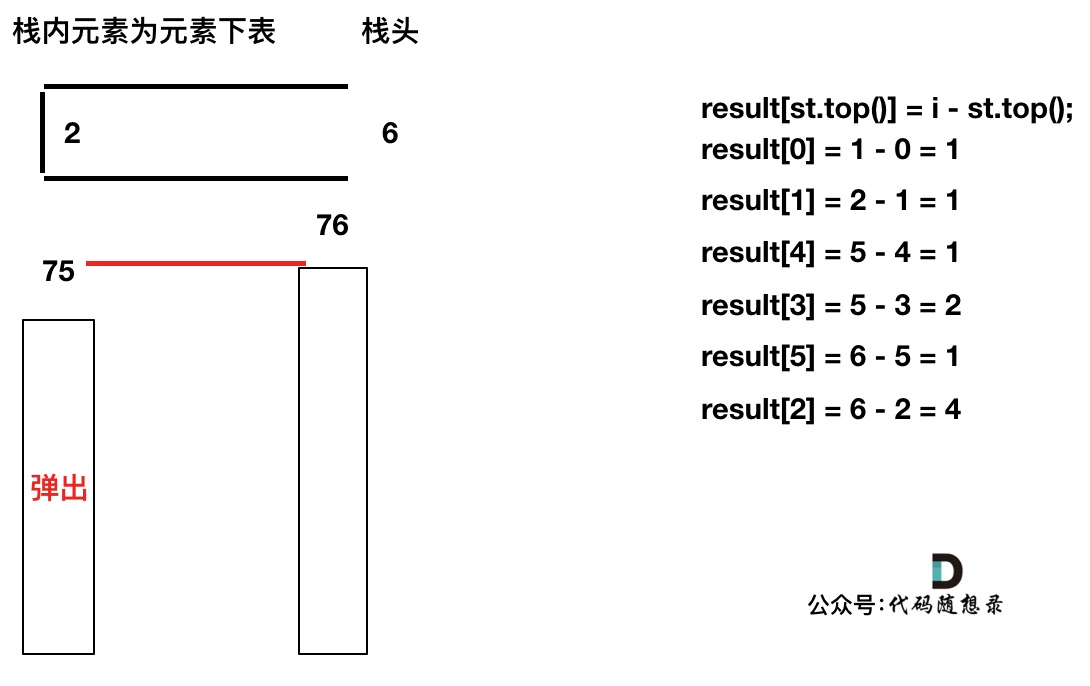
此时栈里只剩下了T[6]

加入T[7], T[7] < T[6] 直接入栈,这就是最后的情况,result数组也更新完了。 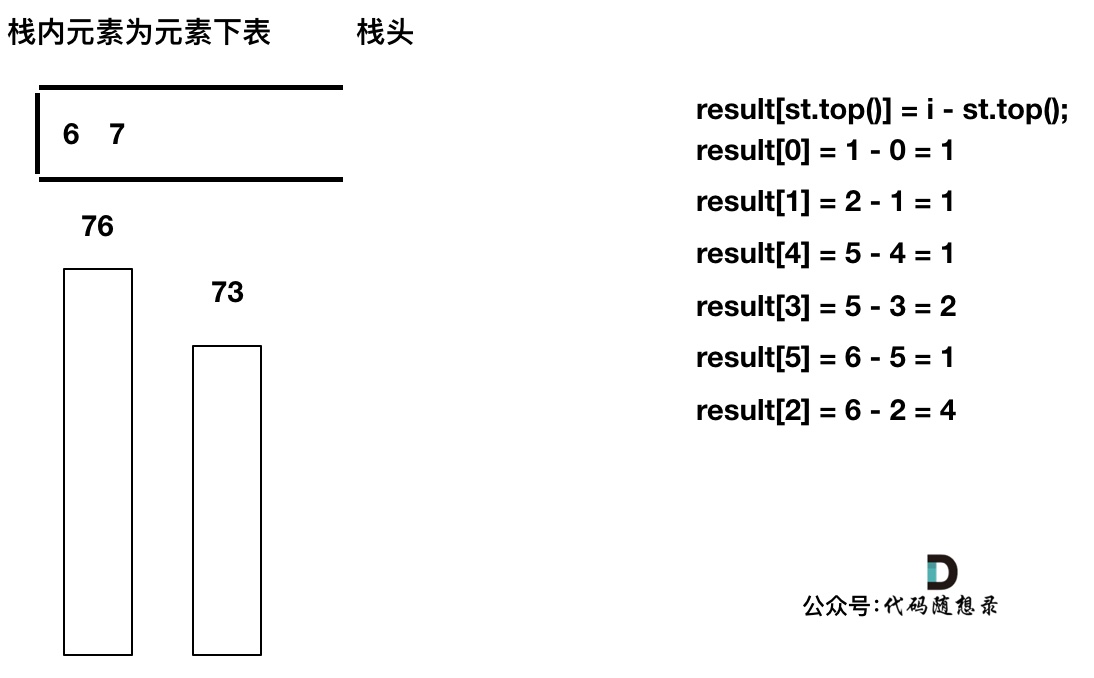
此时有同学可能就疑惑了,那result[6] , result[7]怎么没更新啊,元素也一直在栈里。
其实定义result数组的时候,就应该直接初始化为0,如果result没有更新,说明这个元素右面没有更大的了,也就是为0。
function dailyTemperatures(temperatures: number[]): number[] {
const length: number = temperatures.length;
const stack: number[] = [];
//初始化为全0数组
const resArr: number[] = new Array(length).fill(0);
stack.push(0);
for (let i = 1; i < length; i++) {
let top = stack[stack.length - 1];
while (
stack.length > 0 &&
temperatures[top] < temperatures[i]
) {
//找到比其大的数,更新res数组
resArr[top] = i - top;
//chu'zhan
stack.pop();
top = stack[stack.length - 1];
}
stack.push(i);
}
return resArr;
};
[316] 去除重复字母
给你一个字符串 s ,请你去除字符串中重复的字母,使得每个字母只出现一次。需保证 返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
示例 1:
输入:s = "bcabc"
输出:"abc"
示例 2:输入:s = "cbacdcbc"
输出:"acdb"提示:
1 <= s.length <= 104
s 由小写英文字母组成
字典序问题
字典序(dictionary order),又称 字母序(alphabetical order),原意是表示英文单词在字典中的先后顺序,在计算机领域中扩展成两个任意字符串的大小关系。
返回 字符串,类单调递增栈
首先考虑一个简单的问题:给定一个字符串 s,如何去掉其中的一个字符 ch,使得得到的字符串字典序最小呢?
答案是:找出最小的满足 s[i]>s[i+1] 的下标 i,并去除字符 s[i]。为了叙述方便,下文中称这样的字符为「关键字符」。
在理解这一点之后,就可以着手本题了。一个直观的思路是:我们在字符串 s 中找到「关键字符」,去除它,然后不断进行这样的循环。但是这种朴素的解法会创建大量的中间字符串,我们有必要寻找一种更优的方法。
我们从前向后扫描原字符串。每扫描到一个位置,我们就尽可能地处理所有的「关键字符」。假定在扫描位置 s[i-1] 之前的所有「关键字符」都已经被去除完毕,在扫描字符 s[i] 时,新出现的「关键字符」只可能出现在 s[i] 或者其后面的位置。
于是,我们使用单调栈来维护去除「关键字符」后得到的字符串,单调栈满足栈底到栈顶的字符递增。如果栈顶字符大于当前字符 s[i],说明栈顶字符为「关键字符」,故应当被去除。去除后,新的栈顶字符就与 s[i] 相邻了,我们继续比较新的栈顶字符与 s[i]的大小。重复上述操作,直到栈为空或者栈顶字符不大于 s[i]。
我们还遗漏了一个要求:原字符串 s 中的每个字符都需要出现在新字符串中,且只能出现一次。为了让新字符串满足该要求,之前讨论的算法需要进行以下两点的更改。
在考虑字符 s[i] 时,如果它已经存在于栈中,则不能加入字符s[i]。为此,需要记录每个字符是否出现在栈中。
在弹出栈顶字符时,如果字符串在后面的位置上再也没有这一字符,则不能弹出栈顶字符。为此,需要记录每个字符的剩余数量,当这个值为 0 时,就不能弹出栈顶字符了。
function removeDuplicateLetters(s: string): string {
let stack: string[] = [];
for (let i = 0; i < s.length; i++) {
let ch = s[i];
//当字符串中没有这个字符了,不能做下列操作
if(stack.indexOf(ch) > -1){
continue;
}
while(stack.length > 0 && stack[stack.length - 1] > ch && s.indexOf(stack[stack.length - 1],i) > -1){
//去除关键字符
stack.pop();
}
//入栈
stack.push(ch);
}
return stack.join("");
};
[496] 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
从题目示例中我们可以看出最后是要求nums1的每个元素在nums2中下一个比当前元素大的元素,那么就要定义一个和nums1一样大小的数组result来存放结果。
一些同学可能看到两个数组都已经懵了,不知道要定一个一个多大的result数组来存放结果了。
这么定义这个result数组初始化应该为多少呢?
题目说如果不存在对应位置就输出 -1 ,所以result数组如果某位置没有被赋值,那么就应该是是-1,所以就初始化为-1。
在遍历nums2的过程中,我们要判断nums2[i]是否在nums1中出现过,因为最后是要根据nums1元素的下标来更新result数组。
注意题目中说是两个没有重复元素 的数组 nums1 和 nums2。
没有重复元素,我们就可以用map来做映射了。根据数值快速找到下标,还可以判断nums2[i]是否在nums1中出现过。
const resArr: number[] = new Array(nums1.length).fill(-1);
const stack: number[] = [];
const helperMap: Map<number, number> = new Map();
//判断nums2[i]是否在nums1中出现过,set做为映射
nums1.forEach((num, index) => {
helperMap.set(num, index);
})
栈头到栈底的顺序,要从小到大,也就是保持栈里的元素为递增顺序。只要保持递增,才能找到右边第一个比自己大的元素。
可能这里有一些同学不理解,那么可以自己尝试一下用递减栈,能不能求出来。其实递减栈就是求右边第一个比自己小的元素了。
接下来就要分析如下三种情况,一定要分析清楚。
- 情况一:当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
此时满足递增栈(栈头到栈底的顺序),所以直接入栈。
- 情况二:当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
如果相等的话,依然直接入栈,因为我们要求的是右边第一个比自己大的元素,而不是大于等于!
- 情况三:当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
此时如果入栈就不满足递增栈了,这也是找到右边第一个比自己大的元素的时候。
判断栈顶元素是否在nums1里出现过,(注意栈里的元素是nums2的元素),如果出现过,开始记录结果
function nextGreaterElement(nums1: number[], nums2: number[]): number[] {
//存放结果的数组
const resArr: number[] = new Array(nums1.length).fill(-1);
//存储具体数据在父级索引
const stack: number[] = [];
const helperMap: Map<number, number> = new Map();
//判断nums2[i]是否在nums1中出现过,map做为映射
nums1.forEach((num, index) => {
helperMap.set(num, index);
})
stack.push(0);
for(let i=1,len = nums2.length;i<len;i++){
let top = stack[stack.length -1];
while(stack.length>0&&nums2[top]<nums2[i]){
let index = helperMap.get(nums2[top]);
//判断这个值在不在子集中
if(index!==undefined){
resArr[index] = nums2[i];
}
stack.pop();
//更新栈顶
top = stack[stack.length-1]
}
if(helperMap.get(nums2[i])!=undefined){
stack.push(i);
}
}
return resArr;
[503] 下一个更大元素 II
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
示例 2:输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]
与496类似,但是得遍历两遍。
const index = i % len; 通过取余方法
function nextGreaterElements(nums: number[]): number[] {
const res:number[] = new Array(nums.length).fill(-1);
const stack:number[] = [];
let len = nums.length
stack.push(0);
for(let i=1;i<2*len;i++){
const index = i % len;
let top = stack[stack.length-1];
while(stack.length>0&&nums[top]<nums[index]){
res[top] = nums[index];
stack.pop();
top = stack[stack.length-1];
}
if(i<len){
stack.push(i);
}
}
return res
};
[42] 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:输入:height = [4,2,0,3,2,5]
输出:9
队列---二叉树中有许多
[199] 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]示例 2:
输入: [1,null,3]
输出: [1,3]示例 3:
输入: []
输出: []
[862] 和至少为 K 的最短子数组
标签:number,元素,TS,pop,JS,---,length,push,stack From: https://www.cnblogs.com/guibi/p/16847660.html给你一个整数数组
nums和一个整数k,找出nums中和至少为k的 最短非空子数组 ,并返回该子数组的长度。如果不存在这样的 子数组 ,返回-1。子数组 是数组中 连续 的一部分。
示例 1:
输入:nums = [1], k = 1 输出:1示例 2:
输入:nums = [1,2], k = 4 输出:-1示例 3:
输入:nums = [2,-1,2], k = 3 输出:3