首页 > 其他分享 >K-D Tree

K-D Tree

时间：2025-01-04 16:33:22浏览次数：1  
标签：子树 tar rs int Tree tree ls

网上这个东西都说的云里雾里，而且有很多神秘优化。

板(应该)

给定二维平面上的一些点，要求选择一个基准点使得其他点到它的最远距离-最近距离最小化。

KDT是一种用来维护 \(k\) 维空间点的一种数据结构，是一种二叉树，其上的每一个节点对应这个空间内的一点，并且尽可能保证树的平衡以保证复杂度。

比如说二维平面的这些点的一种建树方案如下：

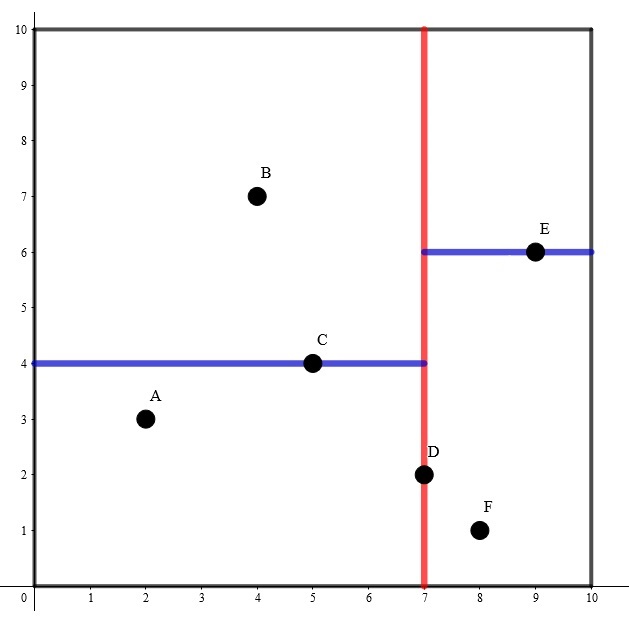
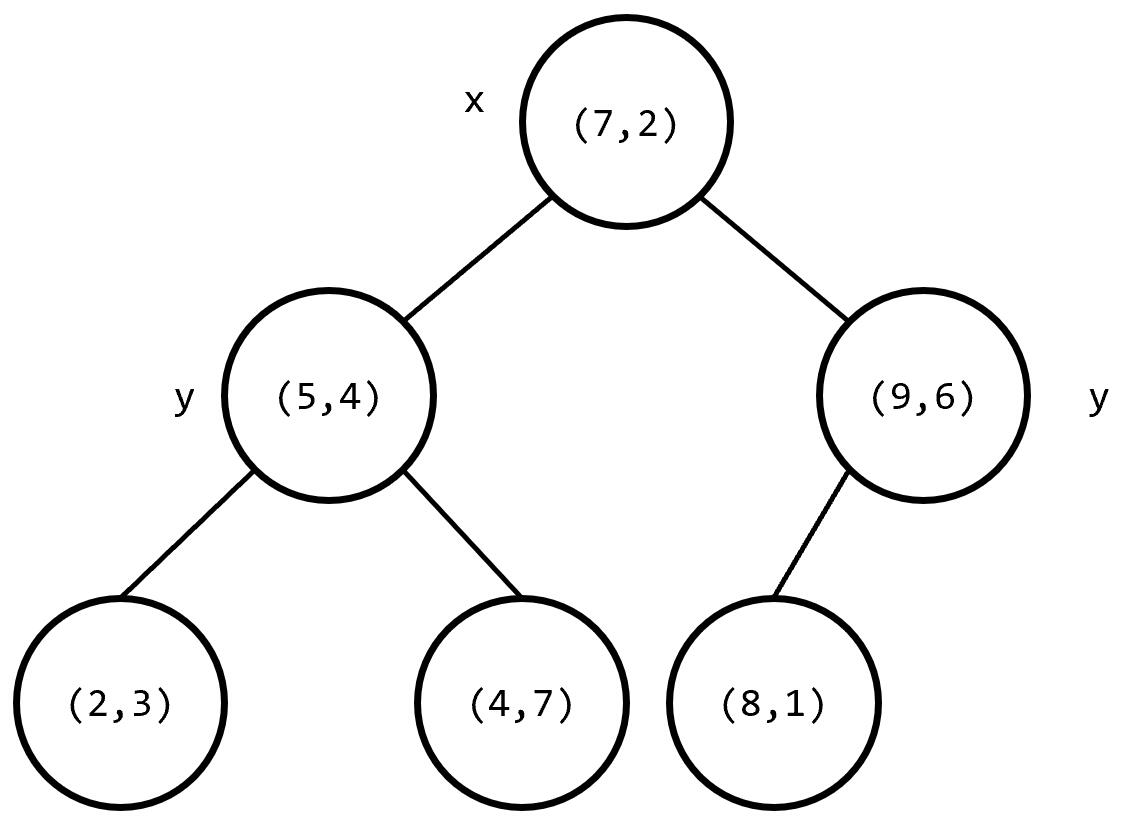
可以发现一个叶子节点唯一地对应分割空间的一个子空间，非叶子节点则代表分割线。关于父亲节点的选取：每次选取的是当前切割维度上当前子空间内点坐标的中位数（可以用一个 nth_element() 函数 \(O(n)\) 找），这样可以使得每次划分的左右子树大小尽量相等。总体的树高是 \(\log n+O(1)\) 的。

关于交替建树

一般建树的维护划分是 \(k\) 个维度轮流建的，这样可以尽量使得子树内在多维都相对接近。

关于一般的查询：

这种是解决矩阵查询问题的，因为kdtree单点就可以分割出两个矩形...就是说查询的时候看一下当前子树的对应矩形和待查询矩形的相交情况，没交点就结束，完全包含就返回，部分包含就递归搜索，和线段树是类似的。这样的查询在二维情况下是 \(O(\sqrt n)\) 的，扩展到 \(k\) 维是 \(O(n^{1-\frac{1}{k}})\)，我不会证。

关于启发式搜索

这个东西的答案查找有的时候是遍历全树（邻域查询，板子题就是）...所以复杂度是炸的，然后就考虑对树进行启发式搜索，就是在父节点处维护当前子树内的估价函数，比如上面的板题，就要求一下查询点和当前点子空间的最远（近）距离，有更新答案的可能才会进，并且两个子树中会优先遍历较优的那个。

关于根号重构：

刚才查中位数的操作只能保证最近这一段操作是平衡的，但是多操作若干次就不平衡了，然后就要根号重构。具体地，设每 \(B\) 次操作进行一次暴力重构（\(B\) 一般取到 \(\sqrt n\)），到了就打tag。

然后还有一个办法是设一个平衡因子，每次发现子树的某个子树大小超过平衡因子就对当前子树重构，这种做法说是基于替罪羊树思想实现的，也是抄来板子里用的方法。

关于二进制分组：

正在施工。

板的代码

#include<bits/stdc++.h>
#define MAXN 100005
#define db double
#define pii pair<int,int>
#define mp make_pair
#define fi first
#define se second
using namespace std;
int n,D,now1,now2;
const int inf=2e9;
const db FIX=0.75;//平衡因子维护平衡 
struct point{
	int x[2];
	bool operator!=(const point &a){
		return x[0]!=a.x[0]||x[1]!=a.x[1];
	}
}a[MAXN],pt[MAXN];
inline bool cmp(point x,point y){
	return x.x[D]<y.x[D];
}
struct KDT{
	#define ls(p) tree[p].lson
	#define rs(p) tree[p].rson
	#define tpx tree[p].p.x
	struct TREE{
		int lson,rson;
		int val;
		point p;
		int xv[2],nv[2];//当前树上节点的：操作次数，所代表的平面点，所代表矩形的的极大极小横纵坐标。 
	}tree[MAXN];
	int tot,rt;
	int bin[MAXN],top; 
	inline void push_up(int p){
		tree[p].val=1;
		tree[p].nv[0]=tree[p].xv[0]=tpx[0];
		tree[p].nv[1]=tree[p].xv[1]=tpx[1];
		if(ls(p)){
			tree[p].val+=tree[ls(p)].val;
			tree[p].xv[0]=max(tree[p].xv[0],tree[ls(p)].xv[0]);
			tree[p].xv[1]=max(tree[p].xv[1],tree[ls(p)].xv[1]);
			tree[p].nv[0]=min(tree[p].nv[0],tree[ls(p)].nv[0]);
			tree[p].nv[1]=min(tree[p].nv[1],tree[ls(p)].nv[1]);
		}
		if(rs(p)){
			tree[p].val+=tree[rs(p)].val;
			tree[p].xv[0]=max(tree[p].xv[0],tree[rs(p)].xv[0]);
			tree[p].xv[1]=max(tree[p].xv[1],tree[rs(p)].xv[1]);
			tree[p].nv[0]=min(tree[p].nv[0],tree[rs(p)].nv[0]);
			tree[p].nv[1]=min(tree[p].nv[1],tree[rs(p)].nv[1]);			
		}
	}//维护一下子树信息 
	inline int newnode(){
		int p=top?bin[top--]:++tot;
		ls(p)=rs(p)=tree[p].val=tree[p].xv[0]=tree[p].nv[0]
		=tree[p].xv[1]=tree[p].nv[1]=tree[p].p.x[0]=tree[p].p.x[1]=0;
		return p;
	}	
	inline void build(int l,int r,int d,int &p){//交替建树（重构建树） 
		if(l>r)return;
		p=newnode();
		D=d;
		int mid=l+r>>1;
		nth_element(pt+l,pt+mid,pt+1+r,cmp);//找中位数 
		tree[p].p=pt[mid];
		build(l,mid-1,d^1,ls(p));
		build(mid+1,r,d^1,rs(p));
		push_up(p);
	}
	inline void clear(int p,int loc){//重构树的删除操作，并按顺序返还节点代表的二维点到原数组 
		if(ls(p))clear(ls(p),loc);
		pt[loc+tree[ls(p)].val+1]=tree[p].p;
		bin[++top]=p;
		if(rs(p))clear(rs(p),loc+tree[ls(p)].val+1);
	}
	inline void update(int &p,int d){//发现一个子树超过平衡因子就重构 
		int c=FIX*tree[p].val;
		if(tree[ls(p)].val>c||tree[rs(p)].val>c){
			clear(p,0);
			build(1,tree[p].val,d,p);
		}
	}
	inline void insert(point tar,int d,int &p){//按维度递归插入点 
		if(!p){
			p=newnode();
			tree[p].p=tar;
			push_up(p);
			return ;	
		}
		if(tar.x[d]<=tpx[d])insert(tar,d^1,ls(p));
		else insert(tar,d^1,rs(p));
		push_up(p);
		update(p,d);//每次插入点后要上传信息和判断重构 
	}
	inline int dis1(int x,int y,int x1,int y1,int x2,int y2){
		return (x<x1?x1-x:(x>x2?x-x2:0))+(y<y1?y1-y:(y>y2?y-y2:0));
	}
	inline void query1(int p,point tar){//对目标点tar查最近点，后一个函数实现是类似的 
		if(!p)return ;
		if(dis1(tar.x[0],tar.x[1],tree[p].nv[0],tree[p].nv[1],tree[p].xv[0],tree[p].xv[1])>now1)return ;//启发式搜索剪枝，子树可能最优解不如当前解就不用跑了 
		if(tree[p].p!=tar)now1=min(now1,dis1(tar.x[0],tar.x[1],tpx[0],tpx[1],tpx[0],tpx[1]));//更新一下答案。 
		int dl=ls(p)?dis1(tar.x[0],tar.x[1],tree[ls(p)].nv[0],tree[ls(p)].nv[1],tree[ls(p)].xv[0],tree[ls(p)].xv[1]):inf;
		int dr=rs(p)?dis1(tar.x[0],tar.x[1],tree[rs(p)].nv[0],tree[rs(p)].nv[1],tree[rs(p)].xv[0],tree[rs(p)].xv[1]):inf;
		if(dl<=dr)query1(ls(p),tar),query1(rs(p),tar);//启发式搜索估价高的 
		else query1(rs(p),tar),query1(ls(p),tar);
	}
	inline int dis2(int x,int y,int x1,int y1,int x2,int y2){
		return max(abs(x-x1),abs(x-x2))+max(abs(y-y1),abs(y-y2));
	}
	inline void query2(int p,point tar){//对目标点tar查最远点 
		if(!p)return ;
		if(dis2(tar.x[0],tar.x[1],tree[p].nv[0],tree[p].nv[1],tree[p].xv[0],tree[p].xv[1])<now2)return ;
		now2=max(now2,dis2(tar.x[0],tar.x[1],tpx[0],tpx[1],tpx[0],tpx[1]));
		int dl=ls(p)?dis2(tar.x[0],tar.x[1],tree[ls(p)].nv[0],tree[ls(p)].nv[1],tree[ls(p)].xv[0],tree[ls(p)].xv[1]):-inf;
		int dr=rs(p)?dis2(tar.x[0],tar.x[1],tree[rs(p)].nv[0],tree[rs(p)].nv[1],tree[rs(p)].xv[0],tree[rs(p)].xv[1]):-inf;
		if(dl>=dr)query2(ls(p),tar),query2(rs(p),tar);
		else query2(rs(p),tar),query2(ls(p),tar);
	}
}Tr;
int ans=inf;
signed main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&a[i].x[0],&a[i].x[1]);
		Tr.insert(a[i],0,Tr.rt);
	}		
	for(int i=1;i<=n;i++){
		now1=inf,now2=-inf;
		Tr.query1(Tr.rt,a[i]);
		Tr.query2(Tr.rt,a[i]);
		ans=min(ans,now2-now1);
	}
	printf("%d\n",ans);
	return 0;
}

最近最远点对

把板子距离从曼哈顿距离改成欧氏距离就没了。但是这题卡kdt，拼尽全力也卡不过去，遂贺了第一篇的人类智慧。

巧克力王国

考虑把给出的 \(x,y\) 当成坐标点用kdt维护，原问题转化为二维平面中有多少个点 \((x,y)\) 满足 \(ax+by<c\)，kdt维护一下块内极大极小值就可以了。

JZPFAR

看似不太可做，仔细看发现k特别小，考虑对每次询问用大根堆维护有限个距离和点编号，启发式搜索的时候直接拿队头比对（因为不关注其他大的答案到底是多少）对头有变的可能再去改。

天使玩偶

这不是我们cdq分治的梗吗。现在来看还是相当板子的，动态加入所以写insert，而且板子里的根号重构这个时候就有用了（一般静态查询其实可以直接build），实现一下求最近点对即可。

崂山白花蛇草水

这题现在还没写完，但是会了所以先记一下。

这会k不小了所以刚才的trick没用，但是矩形查询又确实是很一眼的kdt，转而考虑使用树套树维护。根据tj的意思好像根号重构和外层kdt都会被卡（外层kdt的话内层可能想合并得写可持久化）。

就是外层写一个权值树，内层塞对应权值区间点的kdt，每次查询从线段树上二分答案然后从kdt里矩形查询答案相加即可，kdt的优化要用二进制分组。

标签：子树,tar,rs,int,Tree,tree,ls
From： https://www.cnblogs.com/Claimo0611/p/18652071

相关文章

  • 题解：CF1830A Copil Copac Draws Trees
    首先这道题肯定不能暴力枚举，我们要思考其他算法。我们可以给每一条边编一个号。然后从根开始遍历这棵树，当一条边的编号比他祖先到他祖先的祖先的那条边的编号还要小时，就说明顺序错了，要再等一轮。这个就简单了，直接dfs就行，注意答案要加\(1\)。#include<bits/stdc++.h>using......
  • 比较 HashSet、LinkedHashSet 和 TreeSet 三者的异同
    比较HashSet、LinkedHashSet和TreeSet三者的异同HashSet、LinkedHashSet和TreeSet都是Set接口的实现类，都能保证元素唯一，并且都不是线程安全的。HashSet、LinkedHashSet和TreeSet的主要区别在于底层数据结构不同。HashSet的底层数据结构是哈希表（基于HashMap实现）。L......
  • Trees in python
    TheTreeclassisdefinedasbelow.classTree:""">>>t=Tree(3,[Tree(2,[Tree(5)]),Tree(4)])>>>t.label3>>>t.branches[0].label2>>>t.branches[1].is_leaf()True......
  • WPF使用TreeView和TabControl控件jian实现菜单的选择和切换
    一、页面添加TreeView和TabControl控件1.在MainWindow.xaml页面上添加TreeView控件，设置ItemsSource属性为ViewModel中的TreeList属性，添加<TreeView.ItemTemplate>,在该节点下添加<HierarchicalDataTemplate>,绑定ViewModel中的TreeList下子项中的Children属性，菜单名称绑定Header......
  • 从 Leafy-Tree 到 WBLT
    更好的阅读体验。UPD：2024/12/04添加序列操作UPD：2024/12/10添加可持久化前言前面说过FHQ-treap的缺点在于常数。这次篇文章要讲解WBLT，码量与FHQ-treap差的不多，结构与线段树类似。也可以分裂合并（不推荐），可持久化，但常数远小于FHQ-treap。美中不足的是：需要两倍的空间。......
  • K-D Tree 学习笔记
    注：\(K-D\Tree\)的应用中由于大量用到了\(dfs\)剪枝，所以通常不是正解。但是由于他相当好写，而且通常跑的不慢，所以也广为流传。感觉像是一种半骗分思路。下文简称其为\(KDT\)。一、\(K-D\Tree\)我们都知道\(2D,3D\)表示二维、三维，所以\(KDT\)也很好理解，就是\(K\)维的......
  • 解放磁盘空间的神器——Treesize
    点击蓝字关注我们作者| 风雨软件前言你的电脑磁盘空间很大吗？也许你以为很大，但实际大多数情况是：你用着用着会发现怎么没有空间了？尤其是C盘。  怎么办？那用清理软件清理一下呗！结果，就清理出来几百M，这够给啥用啊！那么，今天我来为大家推荐一款特别强大的磁盘分析工具。Tree......
  • Atcoder_cf17_final_j Tree MST
    这是我的第一道黑题！言归正传，题意是，给定一棵\(n\)个节点的树，现有有一张完全图，两点\(x\),\(y\)之间的边长为\(w_x+w_y+dis_{x,y}\)，其中\(dis_{x,y}\)表示\(x\)和\(y\)在树上的距离，求完全图的最小生成树。常规的求最小生成树的算法有\(kruskal\)、\(prim\)。但是这里这......
  • WPF LogicalTree VisualTree
    <Windowx:Class="WpfApp94.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d="http://schemas.microsoft.......
  • 【Python GUI 编程】tkinter ：Ttk 树视图 Treeview
    在本文中，将介绍TkinterTreeview树视图小部件以及如何使用它来显示表格和分层数据。Tkinter中，没有专门的表格部件，Treeview可以很好地显示表格数据，支持多列显示。要创建Treeview树视图小部件，可以使用以下构造函数：tree=ttk.Treeview(master,**options)Treeview显示表......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99