前言
默认读者会基本的 BST 操作和旋转操作。
本文旋转部分的代码。
rotate(x) 表示将 \(x\) 节点旋转到其父亲节点的位置。
建议阅读:B 树
红黑树
规则
红黑树的平衡不靠平衡因子实时监测,和 treap 的随机值,或像 splay 的均摊。
红黑树的平衡完全靠自身的几条规则。
红黑树有五大规则:
- 所有节点只能是红/黑色。
- 根节点一定是黑色。
- 外部节点(可以理解为 null 节点)为黑色。
- 红色节点的子节点为黑色。(即一条链上一定不会有两个相邻的红色节点)
- 从任意一个外部节点走到根节点所经过的黑色节点数相同(黑高相等)。
靠着这几条规则,红黑树保证了最长路径的长度最多是最短路径的两倍。
所以红黑树是近似平衡的。
比如这些就不是红黑树(旁边是违反的规则编号)。
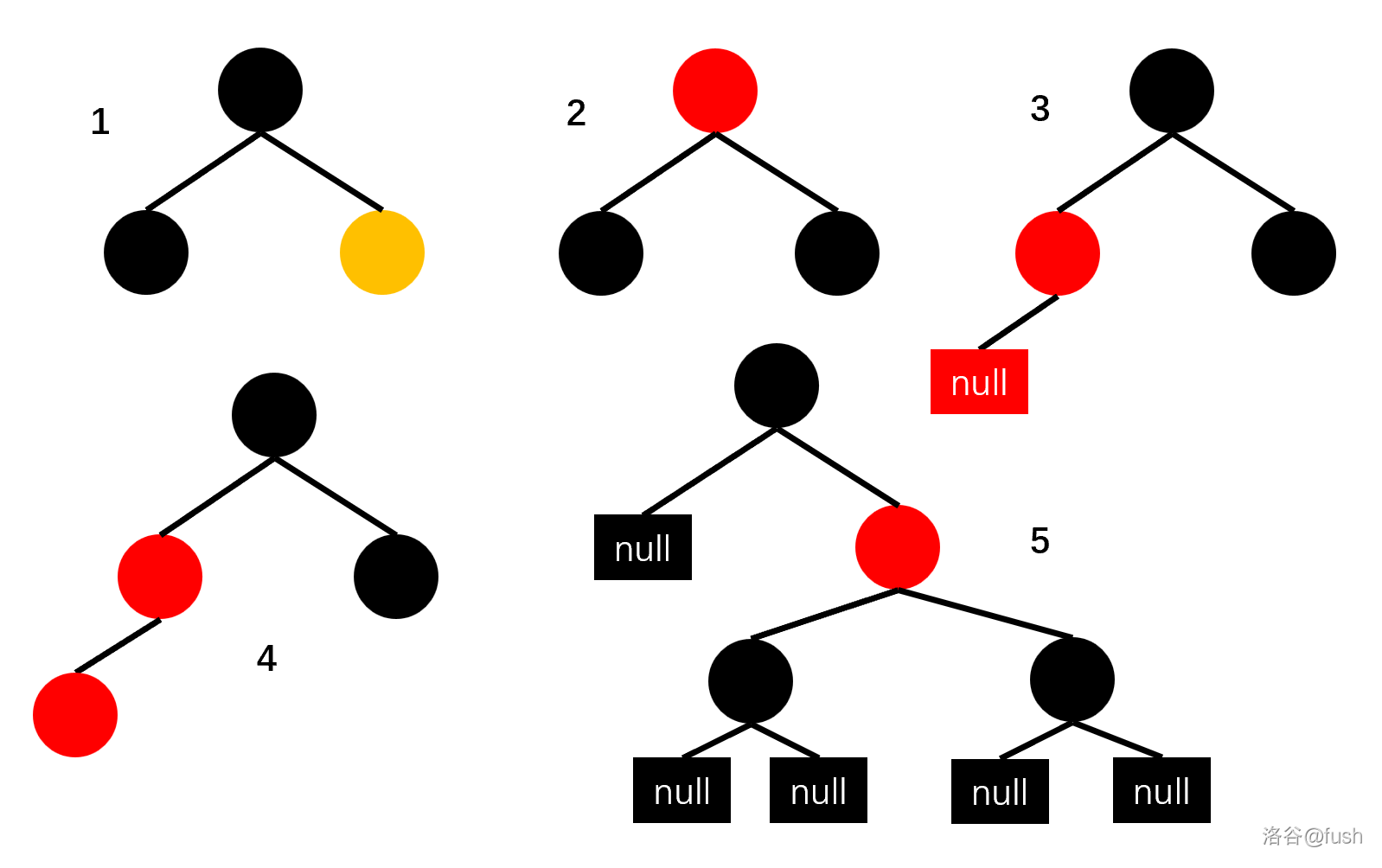
而接下来的图中不会画外部节点。
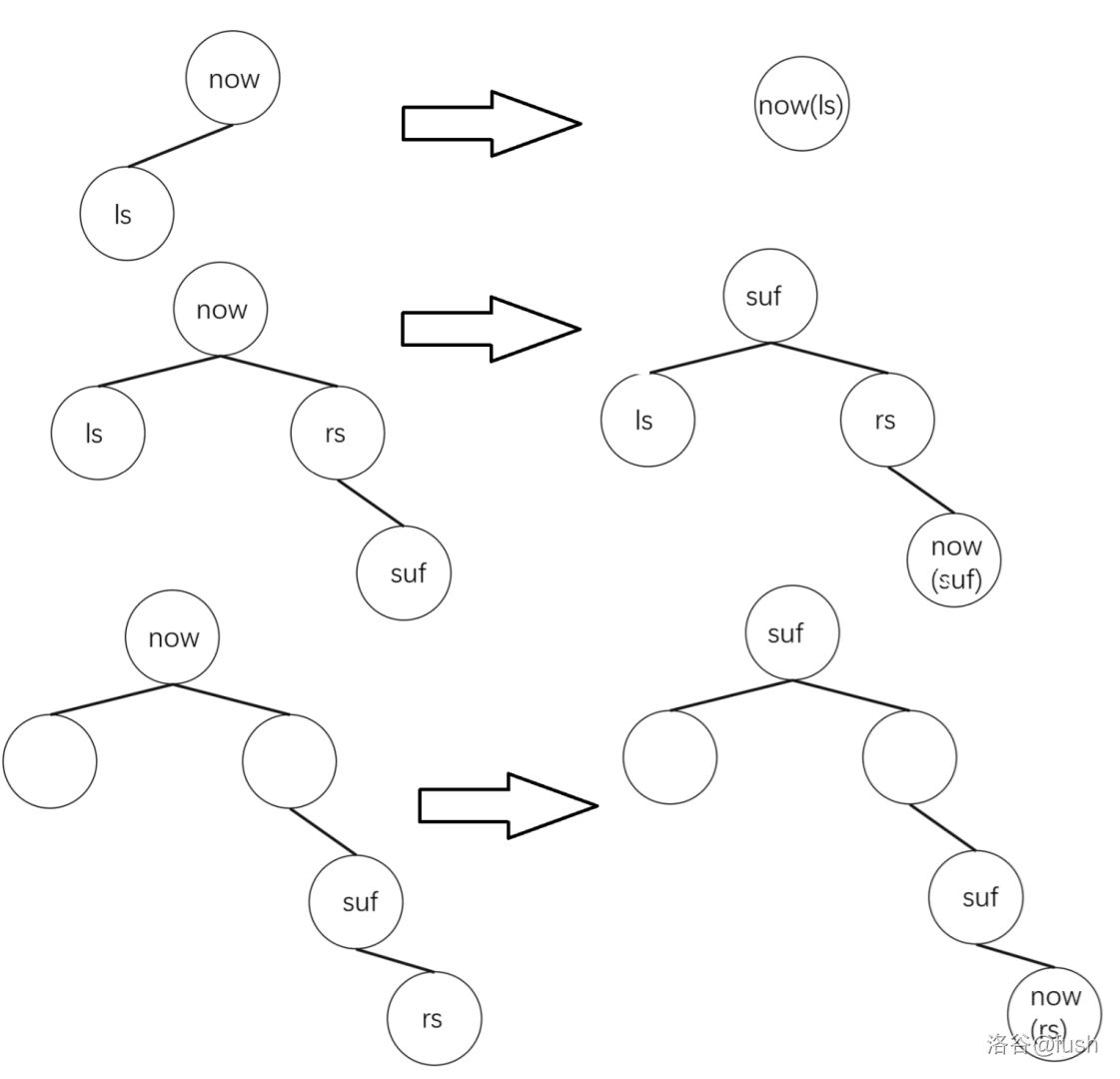
红黑树的等价变化
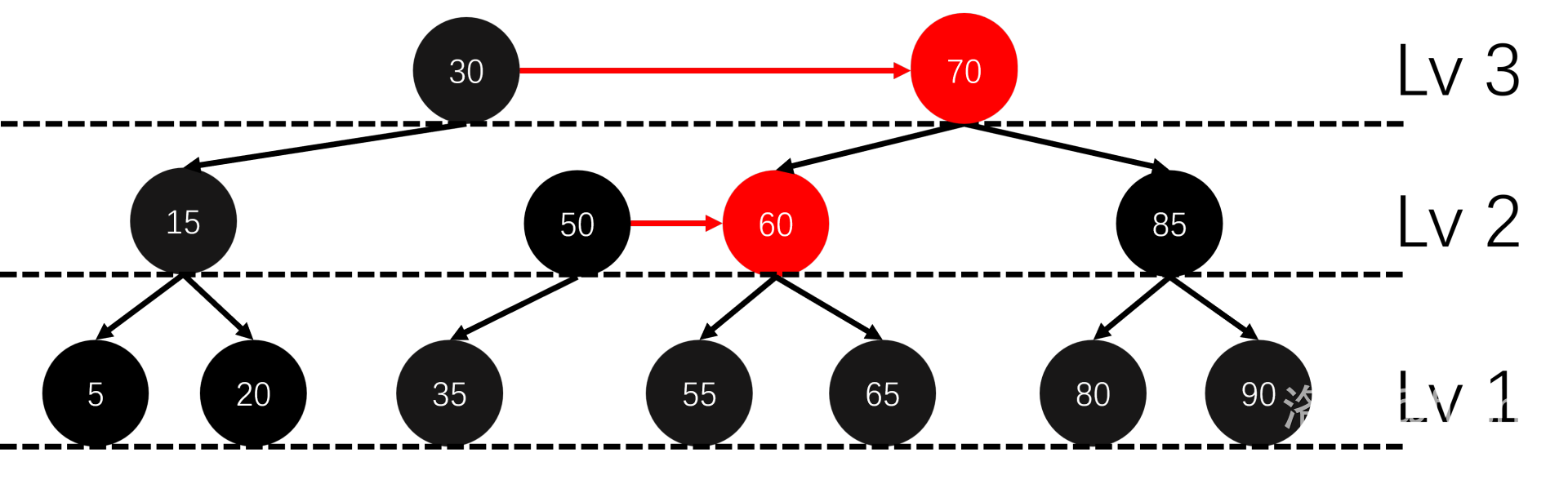
这是一棵红黑树:
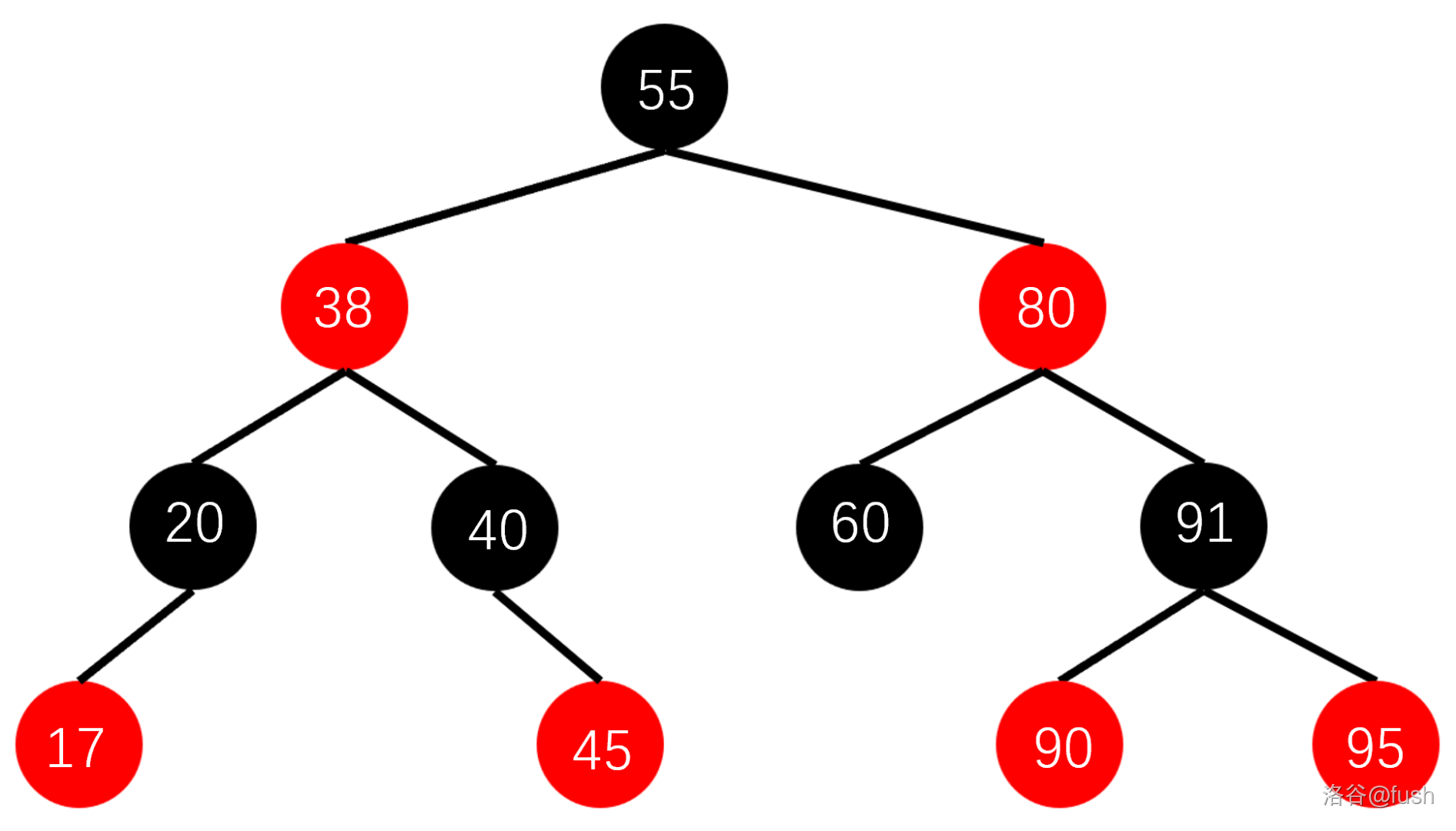
我们把它的红色节点提到其黑色的父亲节点一个高度:
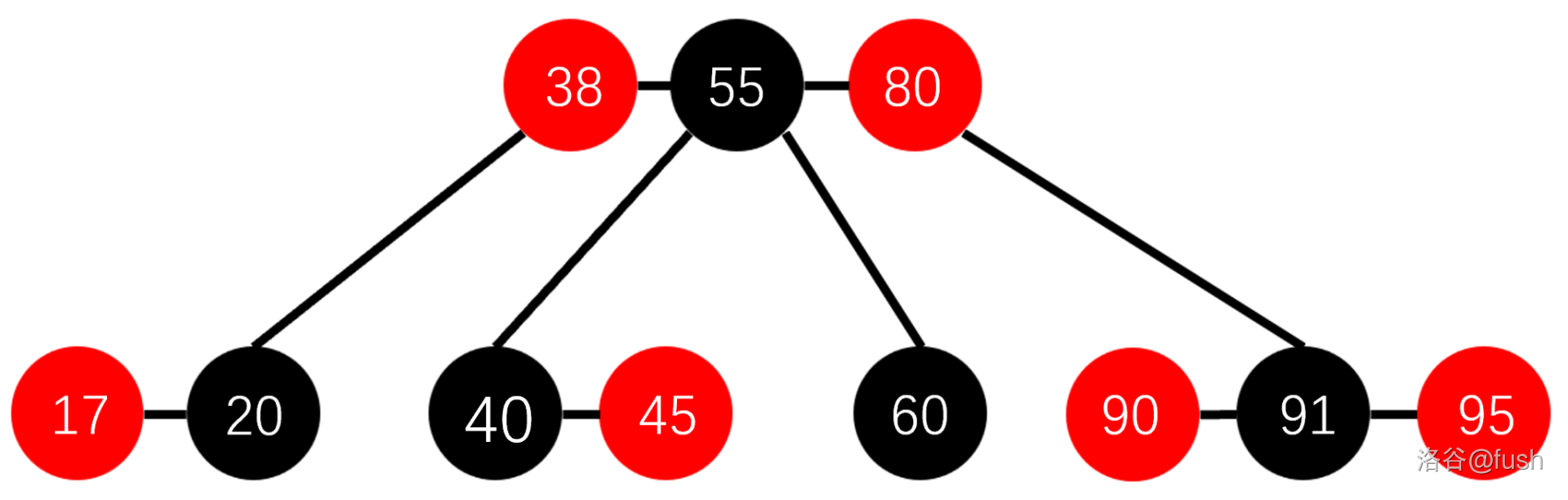
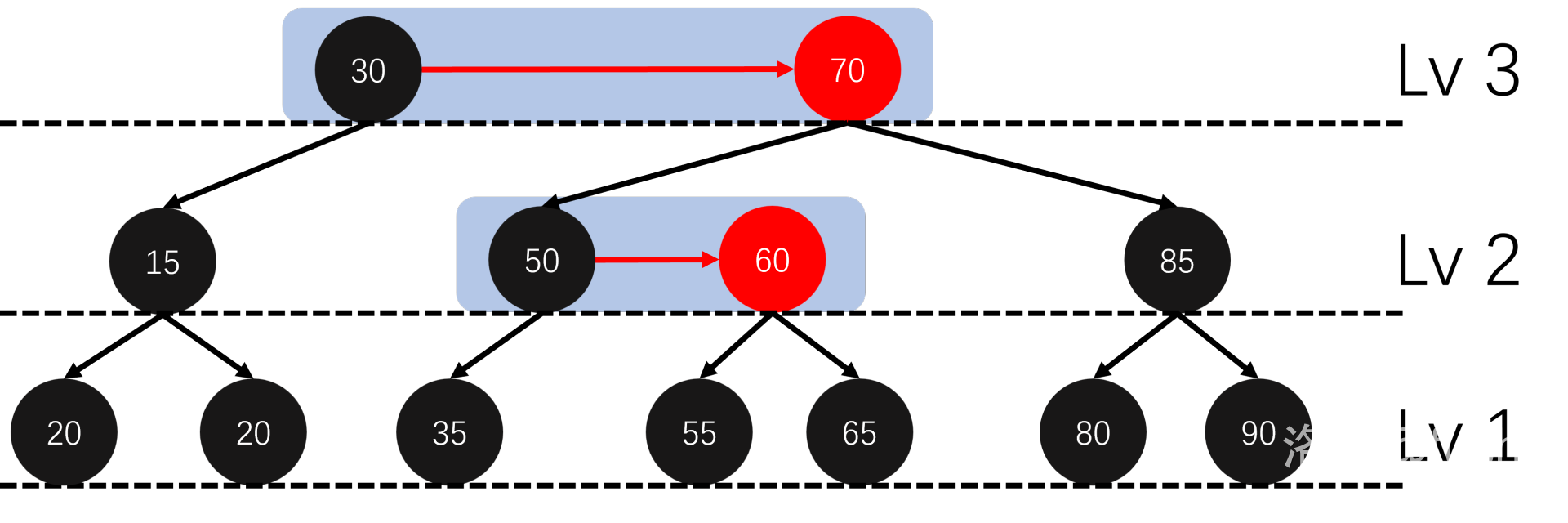
这个结构很明显是一颗 \(4\) 阶 B 树,也就是这样:
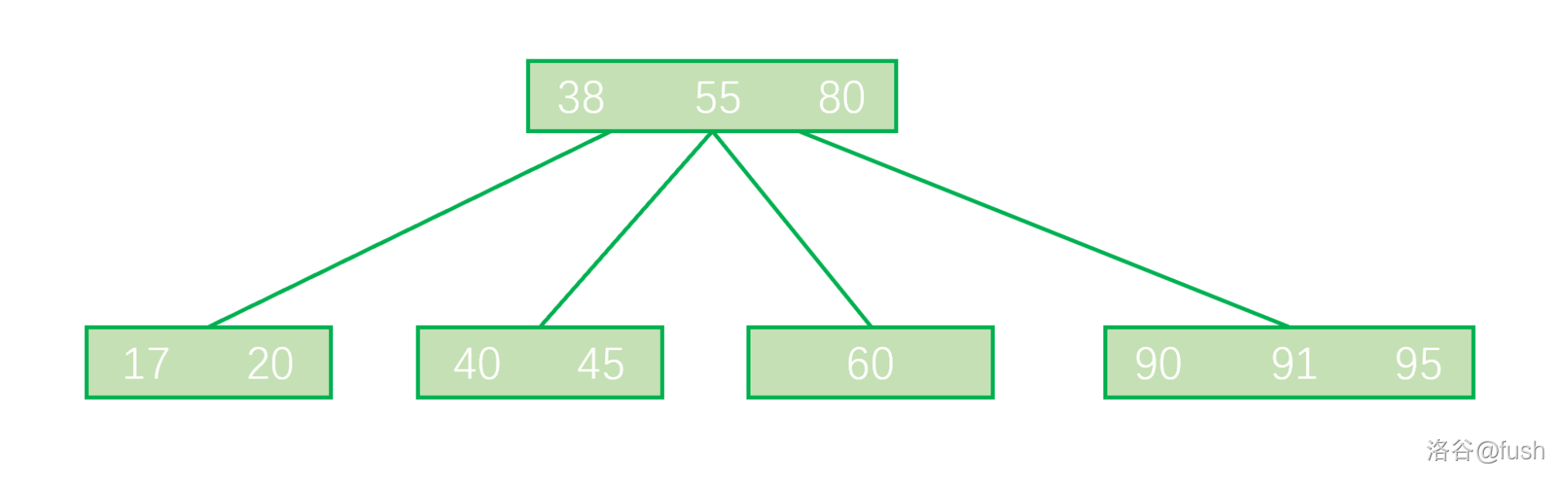
在 1978 年 Leonidas J. Guibas 和 Robert Sedgewick,他们是受 B 树的启发发明了红黑树。
其实我们可以说红黑树和 \(4\) 阶 B 树在结构上是等价的。
但两者不能随意转换。
B 树没有旋转,这种结构对于不区分堆栈的磁盘来说显然比红黑树动态分配节点存储空间要更加合适。
储存的数据都是连续的,对于有着大量连续查询需求的数据库来说更加友好。
而对于小数据量随机插入/查询的需求,由于 B 树的每个节点都存储了若干条记录,所以这时 BST 往往会优于 B 树。
节点定义
struct node{
int val, size, fa, ch[2];
bool col;//0 为黑节点,1 为红节点
}d[N];
#define ls(x) d[x].ch[0]
#define rs(x) d[x].ch[1]
#define fa(x) d[x].fa
int root, tot = 0, stk[N], top = 0;
void pushup(int x){d[x].size = 1 + d[ls(x)].size + d[rs(x)].size;}
#define get(x) (x == rs(fa(x)))
int newnode(int val){
int w = top ? stk[top--] : ++tot;
d[w].val = val, d[w].col = d[w].size = 1;
fa(w) = ls(w) = rs(w) = 0;
return w;
}
插入
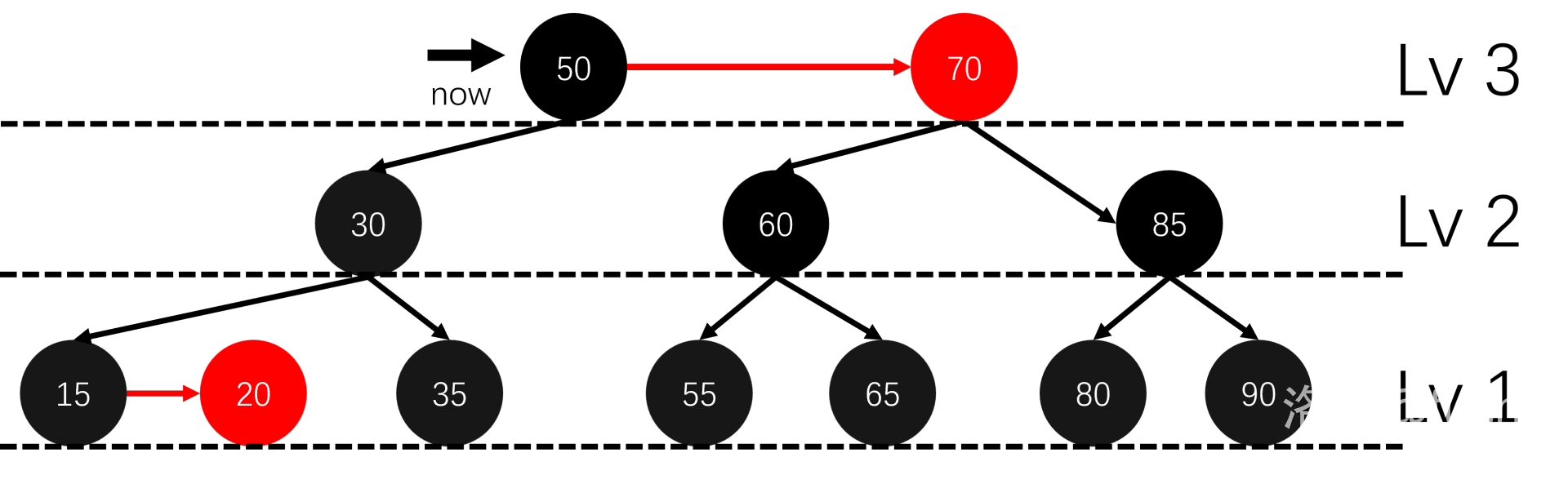
我们肯定会选择插入红色节点,因为它不会影响黑高(一个外部节点走到根节点所经过的黑色节点数)。
那么什么时候会违反规则。
自然是父亲节点也是红色的时候。
这时一条链上就有了两个红色节点,我们考虑修正。
我们用 \(now\) 表示需要修正的节点,\(fa\) 表示其父节点,\(gf\) 表示 \(fa\) 的父节点,\(ul\) 表示 \(gf\) 的另一个儿子节点。
我们先讨论 \(fa\) 在左边的情况(右侧同理):
- 祖父节点的另一个子节点为黑色:
我们有两种情况:
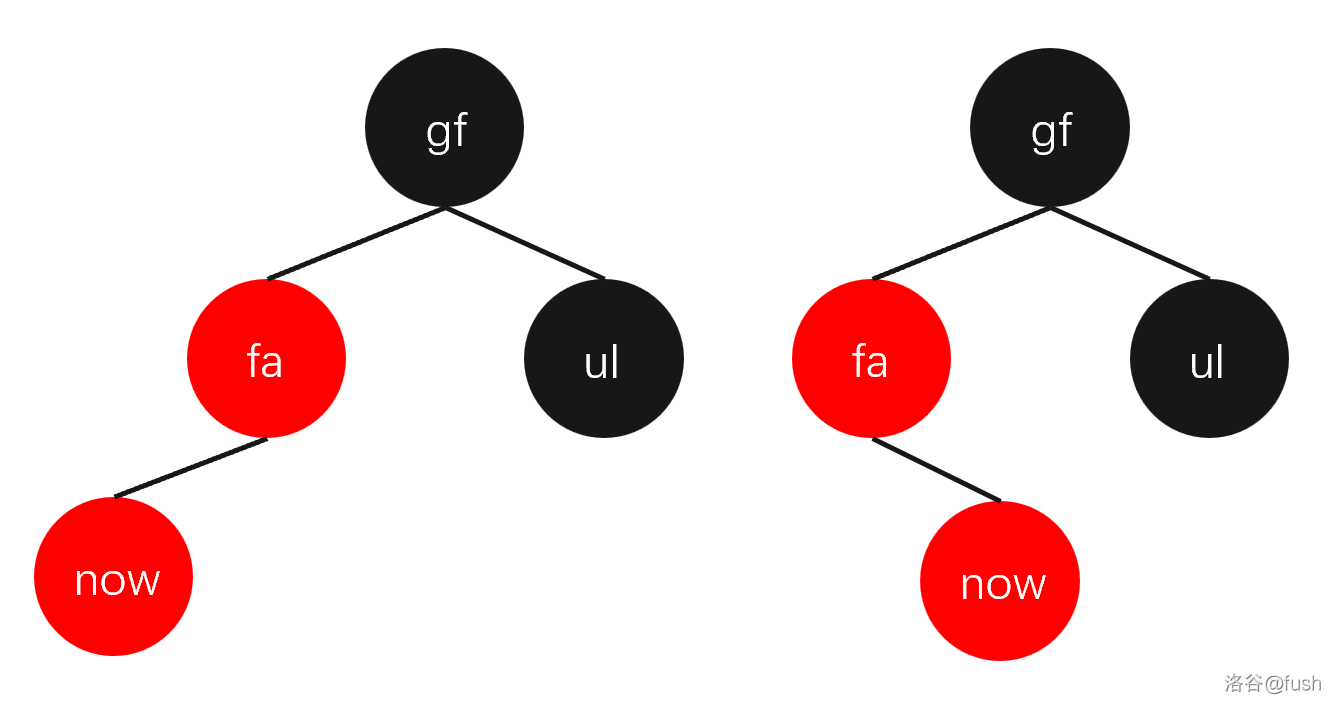
我们会把第二种变成第一种:
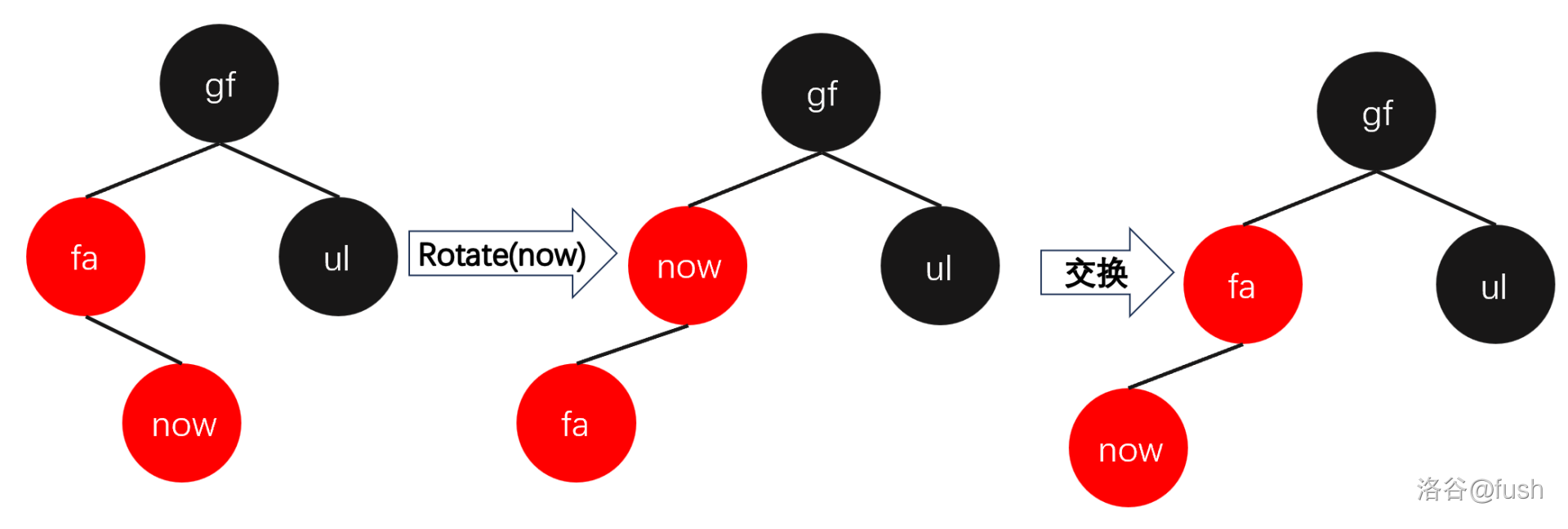
然后修正,先将 \(fa\) 节点旋转上去,然后翻转 \(gf, fa\) 节点的颜色。
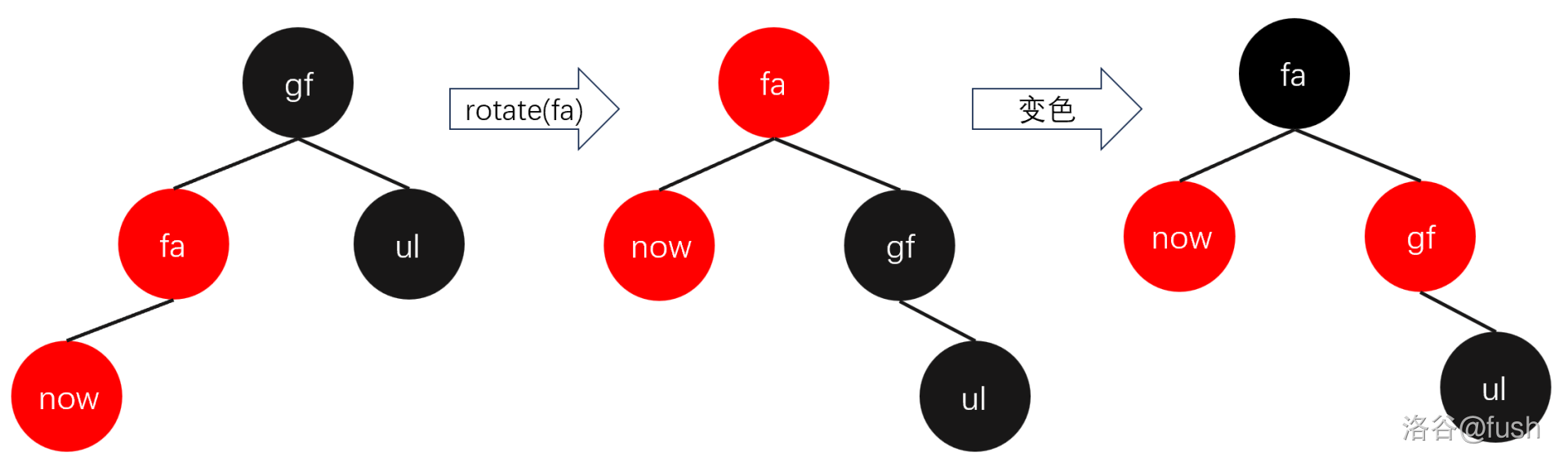
这样子两边的黑高没有变化,也不会有两个连续的红色节点了,就结束了。
代码片段:
if(d[ul].col == 0){
if(get(now) == get(f))rotate(now), swap(now, f);
d[gf].col = 1, d[f].col = 0, rotate(f);
break;
}
- 祖父节点的另一个子节点为红色:
我们翻转 \(f, ul, gf\) 节点的颜色。
虽然没有改变黑高,但是 \(gf\) 节点和其父节点也有可能冲突。
所以我们让 \(now \gets gf\),继续向上走。
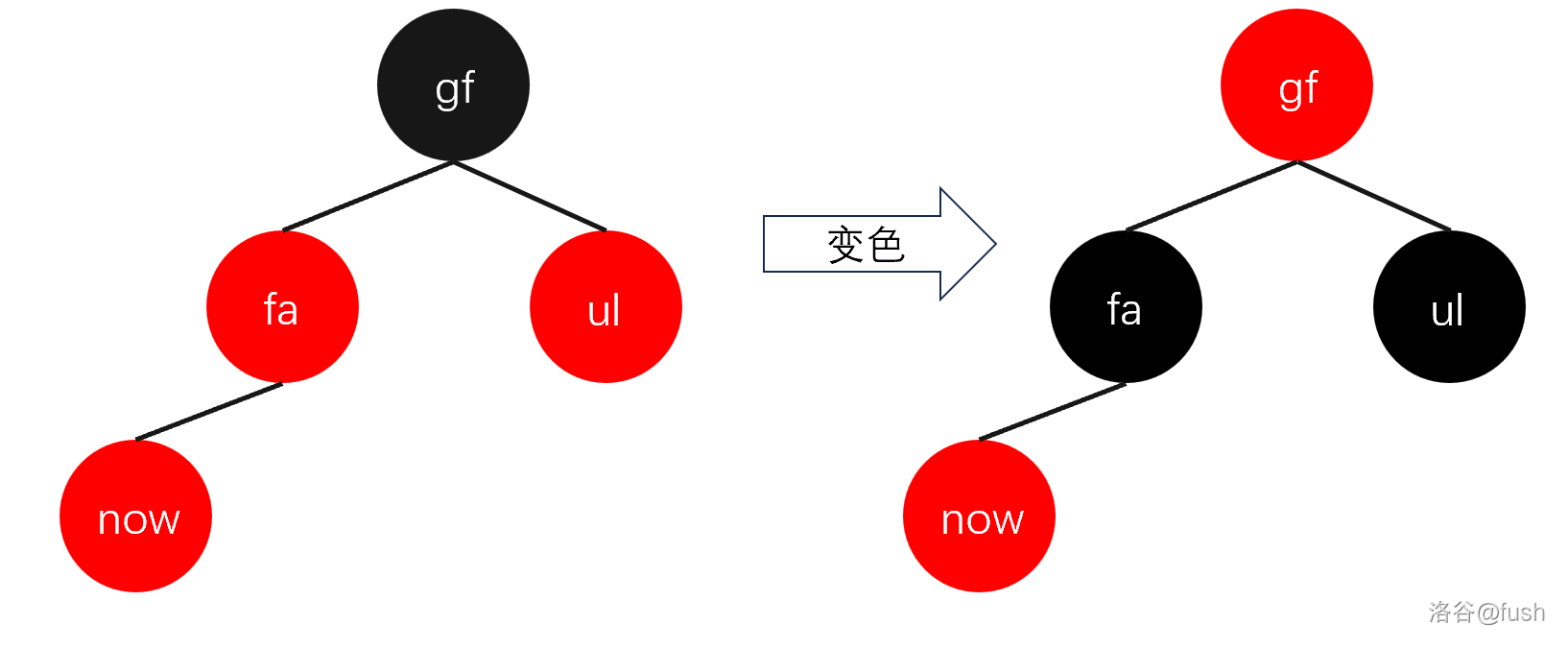
因为根节点一定是黑色的,所以当我们遍历到根节点的时候必然会停止。
修正部分的代码:
while(d[fa(now)].col){
int f = fa(now), gf = fa(f);
int w = !get(f), ul = d[gf].ch[w];
if(d[ul].col)d[f].col = d[ul].col = 0, d[gf].col = 1, now = gf;//第二种
else{//第一种
if(get(now) == w)rotate(now), swap(now, f);//旋转
d[gf].col = 1, d[f].col = 0, rotate(f);
break;
}
}
d[root].col = 0;
同时,由于链长是 \(\log n\),故这样的递归最坏复杂度是 \(\log n\) 级别的。
删除
如果我们要删除的节点不是叶子结点。
那么我们就不能直接删除了。
如果它只有一个儿子,那么我们让它的儿子顶替它。
否则,它有两个儿子:
我们将它和它的后缀进行交换。
虽然会暂时违反红黑树的性质,不过这并没有关系。
而它的后缀至多会有一个儿子。
如果有,我们就让它的右儿子顶替它就好了。
替换部分的代码:
int w = now, g = 0;
if(ls(now) && rs(now)){//找到后继
w = rs(now);
while(ls(w)) w = ls(w);
}
g = d[w].ch[!ls(w)], fa(g) = fa(w);//g 为顶替的节点
if(!fa(w))root = g;
else d[fa(w)].ch[get(w)] = g;
d[now].val = d[w].val;
for(int i = fa(w); i; i = fa(i))d[i].size--;//更新 size
我们再想想平衡:
如果删除节点是红色的,那么没有任何事情。
但如果是黑色的,那就麻烦了。
图中的空节点表示任意颜色
我们用 \(now\) 表示需要修正的节点(黑高少一),\(fa\) 便是 \(now\) 的父亲节点,\(ul\) 表示 \(fa\) 节点的另一个儿子。
先考虑 \(now\) 在左侧:
- 其父亲节点的另一个节点(\(ul\))为黑色:
又有两种情况:
\(\qquad\) 1. \(ul\) 节点至少一个红儿子
\(\qquad\)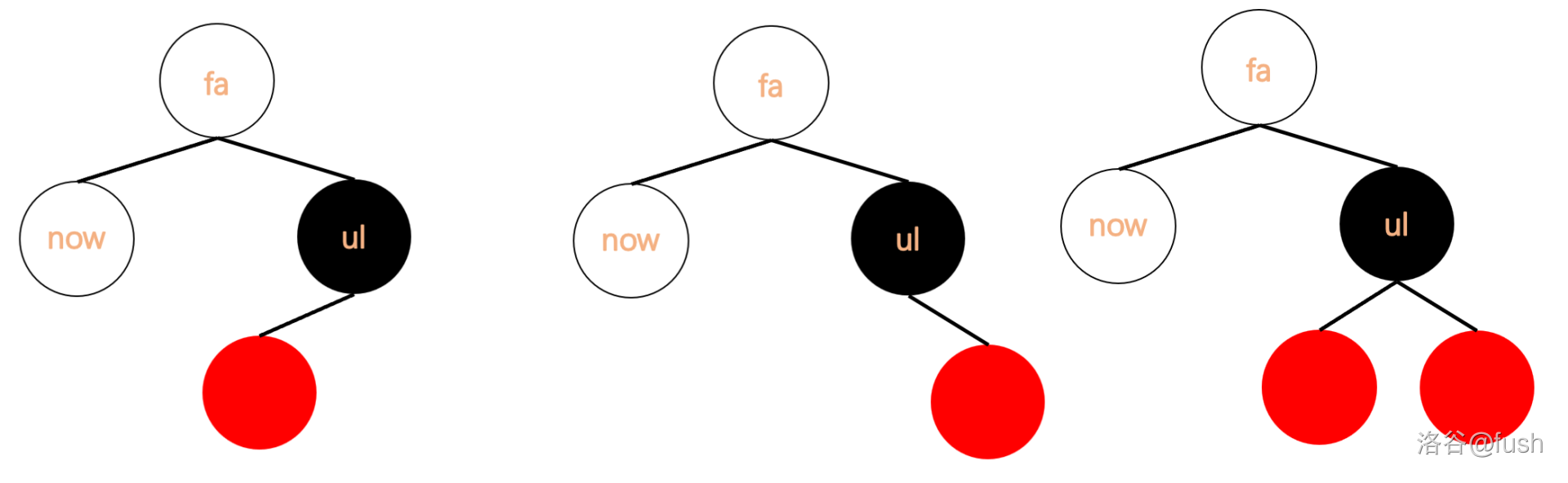
\(\qquad\) 对于第一种我们进行旋转和变色后变成第二种。
\(\qquad\)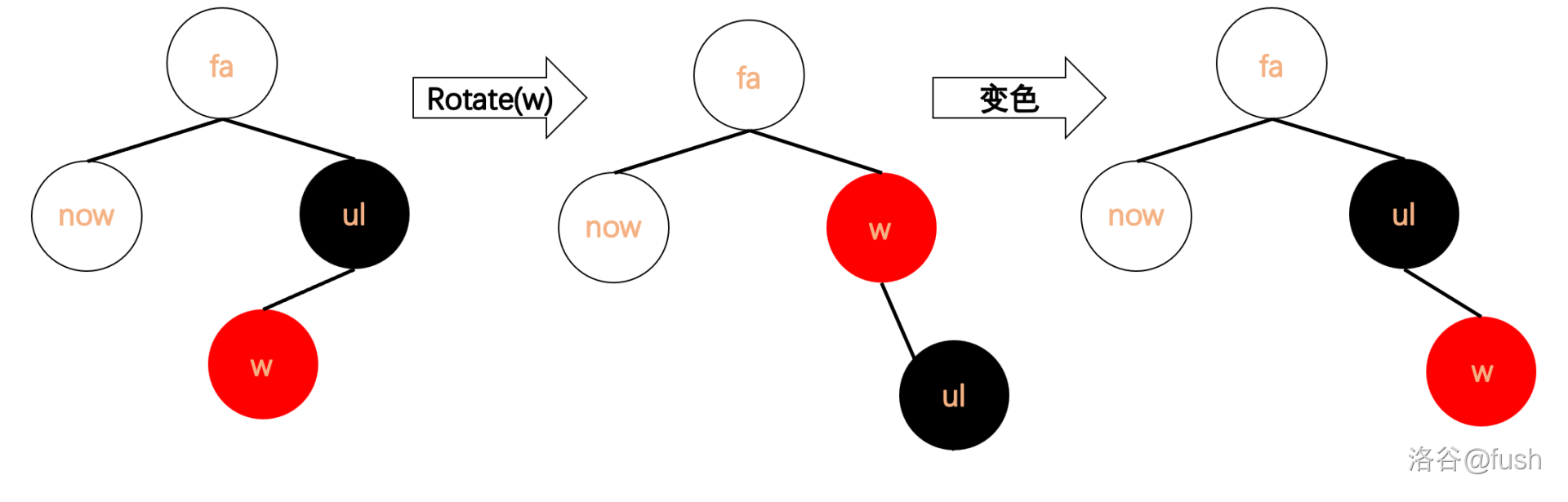
\(\qquad\) 这样 ul 节点的右儿子就一定是红色了。
\(\qquad\) 然后修正,先旋转 \(ul\) 节点,然后交换 \(ul\) 和 \(fa\) 节点的颜色,将 \(ul\) 的右儿子变为黑色。
\(\qquad\)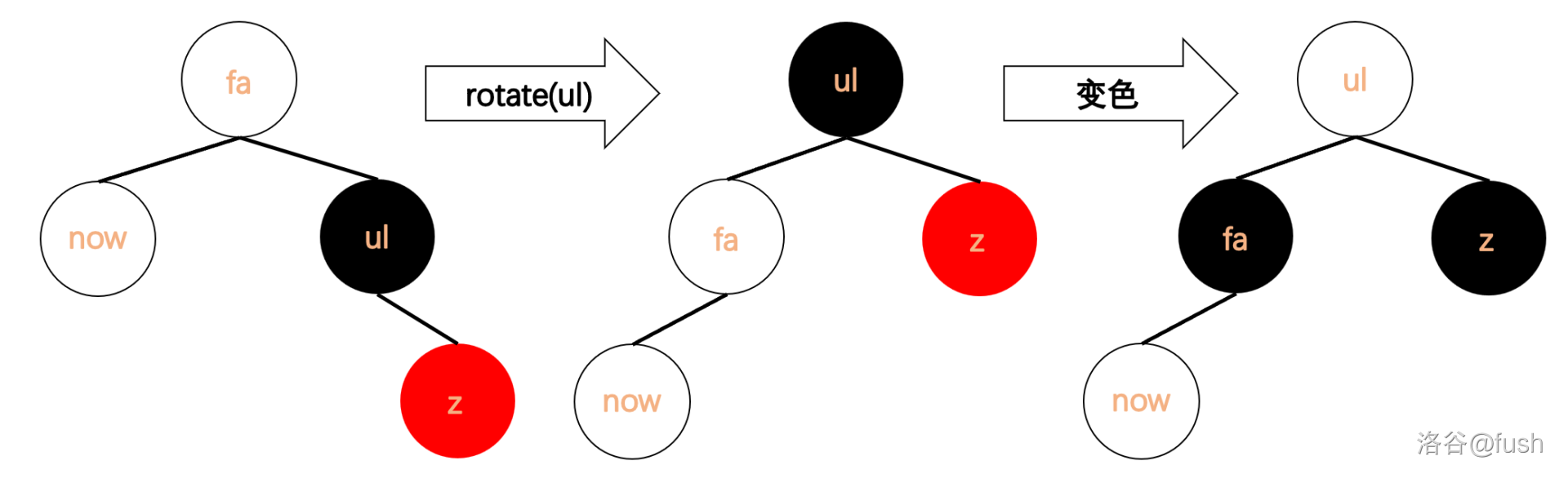
\(\qquad\) 2. \(ul\) 节点没有红儿子
\(\qquad\) 将 \(ul\) 节点的颜色翻转。
\(\qquad\) 那么如果 \(fa\) 节点是红色,变成黑色就结束了。
\(\qquad\) 否则,虽然 \(fa\) 是平衡的,但黑高少 \(1\),所以继续向上修正。 - 其父亲节点的另一个节点为红色:
旋转 \(ul\) 节点,再交换 \(fa\) 节点和 \(ul\) 节点的颜色。
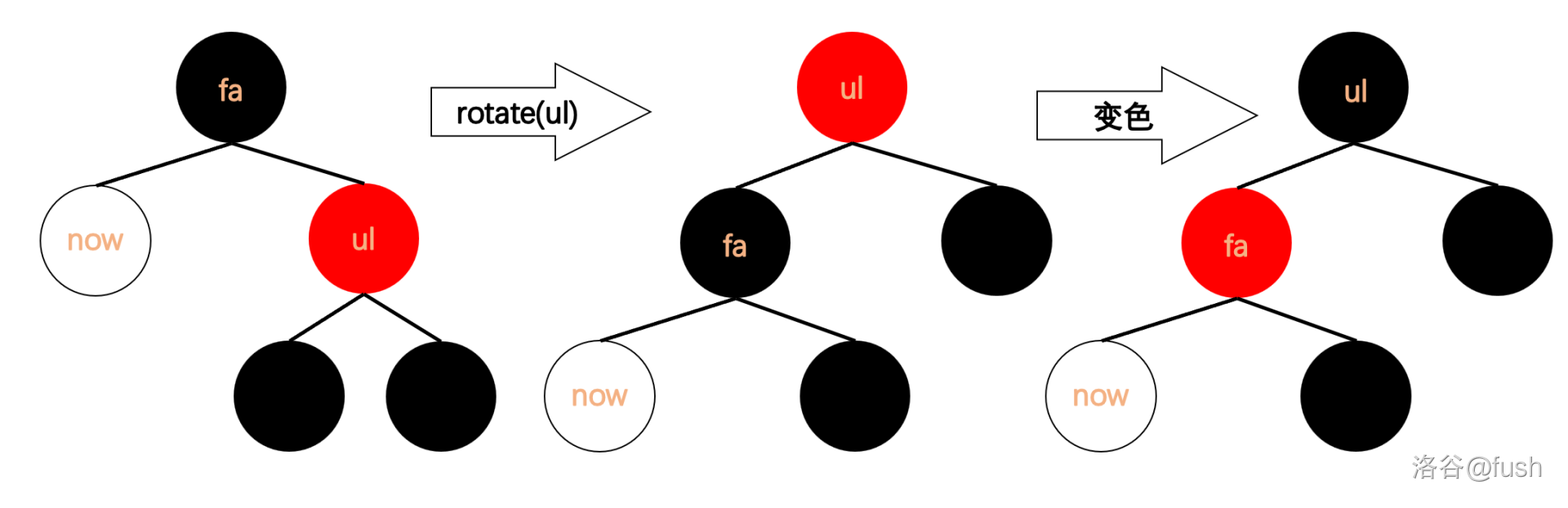
明显黑高没有变化,但 \(ul\) 节点是黑色的了,这样就可以套用之前的修正方式了。
修正部分的代码:
while(now != root && !d[now].col) {
bool w = !get(now);
int f = fa(now), ul = d[f].ch[w];
if(d[ul].col)d[ul].col = 0, d[f].col = 1, rotate(ul);//ul 节点是红色
else if(!d[ls(ul)].col && !d[rs(ul)].col)d[ul].col = 1, now = f;//ul 节点没有红儿子
else{
if(!d[d[ul].ch[w]].col){//右侧没有红儿子
d[d[ul].ch[!w]].col = 0, d[ul].col = 1;
rotate(d[ul].ch[!w]), ul = d[f].ch[w];
}
d[ul].col = d[f].col;
d[d[ul].ch[w]].col = d[f].col = 0;
rotate(ul);
break;
}
}
d[now].col = 0;
代码
AA 树
AA 树简介
定义
AA 树是 Arne Andersson 教授在 \(1993\) 年在他的论文 Balanced search trees made simple 中介绍,设计的目的是减少红黑树考虑的不同情况。
AA 树规定红色节点必然是右儿子。
AA 树为了实现方便,没有使用红黑两种颜色,而是使用 \(level\) 维护平衡。
AA 树有一下性质:
- 空节点 \(level\) 为 \(0\)。
- 左子节点的 \(level\) 为父节点 \(level - 1\),而叶节点 \(level\) 必为 \(1\)。
- 右子节点的 \(level\) 为父节点 \(level\) 或父节点 \(level - 1\),但是一定小于爷爷的 \(level\)。
- \(level > 1\) 的节点有两个子节点。
这就是一颗 AA 树:
节点定义
struct node{
int val, ls, rs, size, lv;
}d[N];
int root, tot = 0, stk[N], top = 0;
void pushup(int x){d[x].size = 1 + d[d[x].ls].size + d[d[x].rs].size;}
int newnode(int val){
int w = top ? stk[top--] : ++tot;
d[w].val = val, d[w].lv = d[w].size = 1;
return d[w].ls = d[w].rs = 0, w;
}
平衡维护
水平链接
子节点的 \(level\) 等于父节点的 \(level\) 的链接被称为水平链接,类似于红黑树中的红节点。
允许单独的右水平链接,但不允许连续的右水平链接,不允许左水平链接。
被框起来的就是水平链接。
插入和删除操作可能会暂时导致 AA 树失去平衡。
恢复平衡只需要两种不同的操作:skew(斜化)和 split(分裂)。
split 解决连续的水平链接,skew 解决左水平链接。
保持平衡的插入和删除的实现通过依赖 skew 和 split 操作来仅在需要时修改树。
而不是由调用者决定是否进行 skew 或 split,从而变得更加简化。
split
先考虑违反第 \(3\) 条的维护。
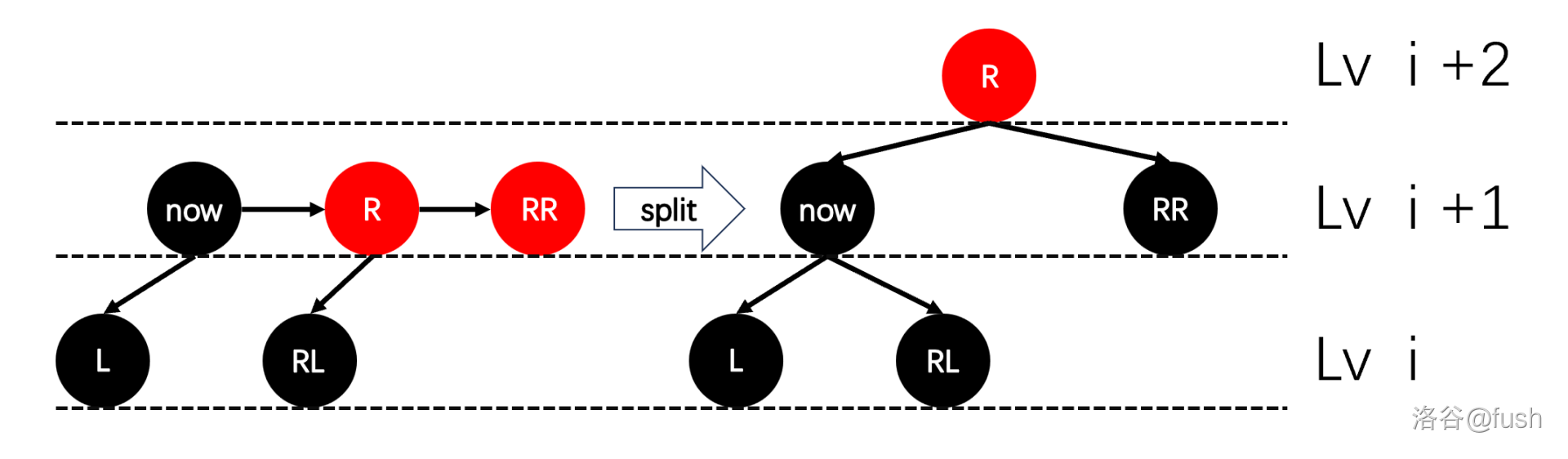
也就相当于对 \(R\) 节点旋转,然后把 \(level_{R} \gets level_{R} + 1\)(维护第 4 条)。
void split(int&x){
if(!x)return;
node &now = d[x], &r = d[now.rs];
int z = x;
if(d[r.rs].lv == now.lv)
x = now.rs, now.rs = r.ls, r.ls = z, r.lv++, pushup(z), pushup(x);
}
skew
考虑违反第 \(2\) 条的维护。
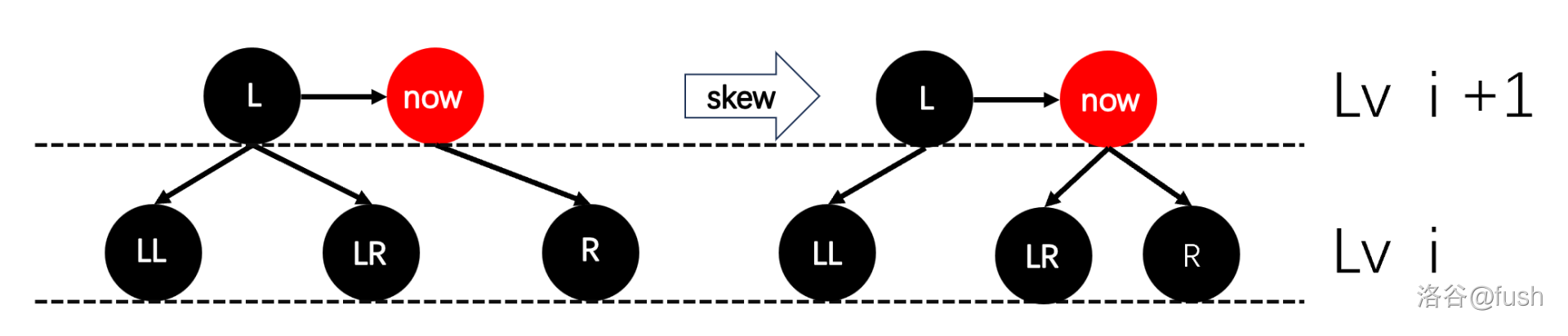
肯定有人好奇 \(LR\) 为什么是黑色。
因为 \(L\) 要么是 split 上来的,要么就是叶子节点,所以 \(LR\) 必然为黑色。
但如果 \(R\) 节点是红色的,那就会违反条件 \(3\) 了,就要再调用 split。

void skew(int&x){
if(!x)return;
node &now = d[x], &l = d[now.ls];
int z = x;
if(l.lv == now.lv)
x = now.ls, now.ls = l.rs, l.rs = z, pushup(z), pushup(x);
}
插入
AA 树的 insert 和几乎普通二叉搜索树是一样的。
新节点一定作为叶节点插入,记得新插入的叶节点 \(level\) 应该为 \(1\)。
void insert(int&x, int val){
if(!x)x = newnode(val);
else if(d[x].val > val)insert(d[x].ls, val);
else insert(d[x].rs, val);
skew(x), split(x), pushup(x);
}
不同的是,在 insert 过程中,可能破坏沿途节点的性质。
所以每个途径节点上先 skew 一次,再 split 一次(因为上文说过 skew 后可能又产生连续红边)。
删除
如果删除节点没有儿子,那么直接删除。
如果有一个儿子,那么顶替,并染色为黑。
否则用后继交换,由于 AA 树除了 \(level = 1\) 的,其他必然有左儿子,所以交换后一定是在叶子节点。
如果我们删除的是红色叶子节点,这对树的平衡没有任何影响。
我们需要考虑的是删除黑色节点的时候。
例如我们要删除这棵树的节点 \(5\)。

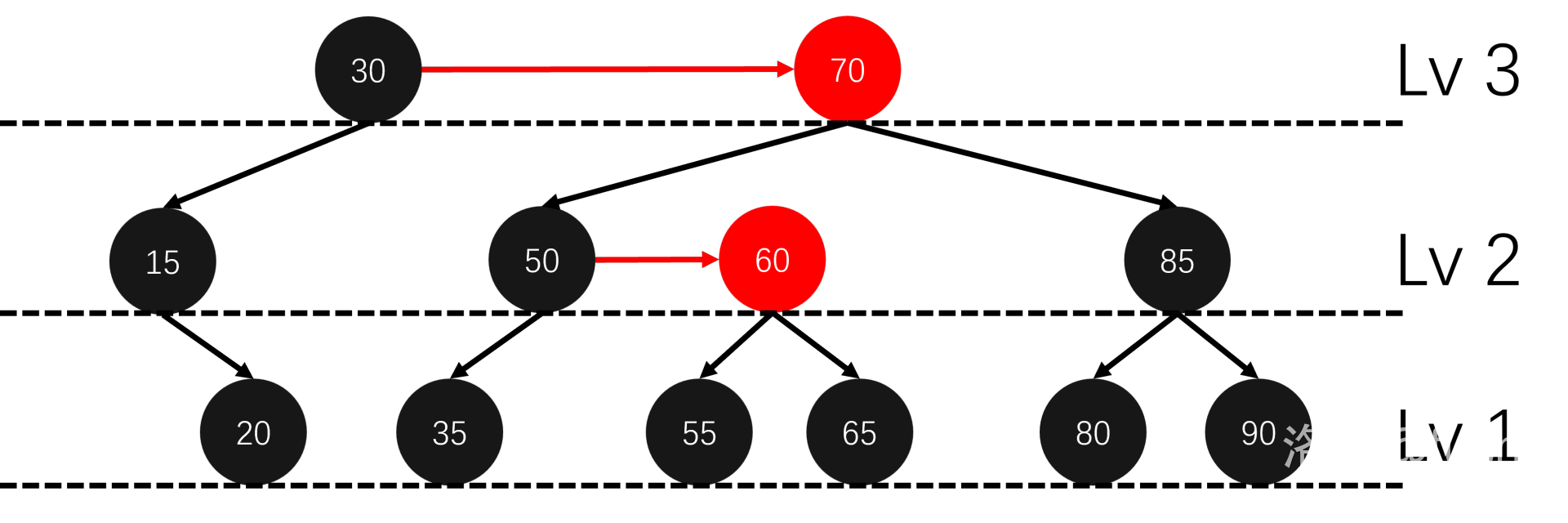
接下来考虑平衡。
我们从底向上递归考虑。
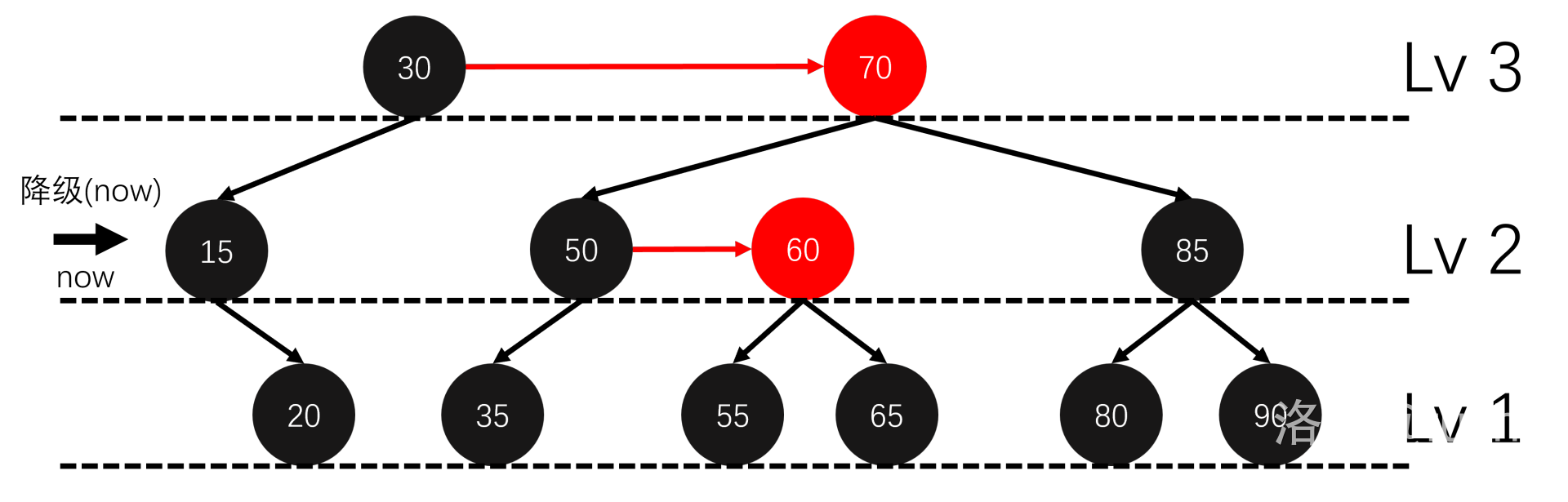
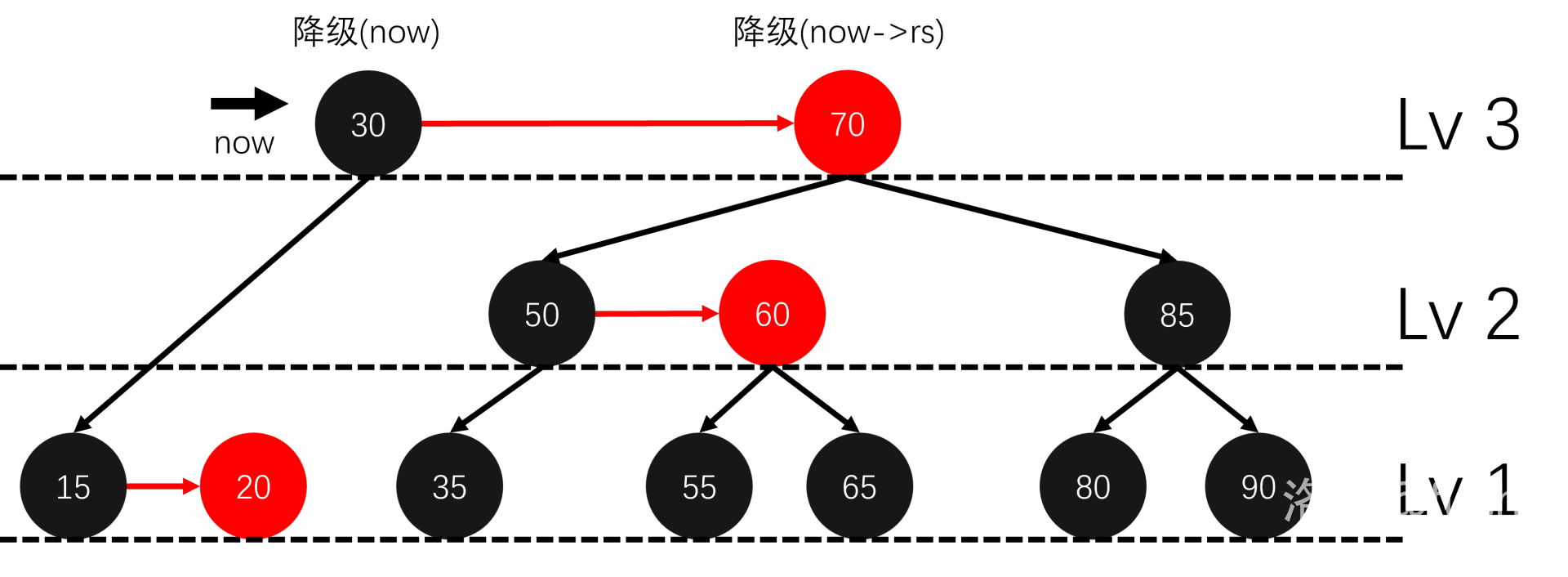
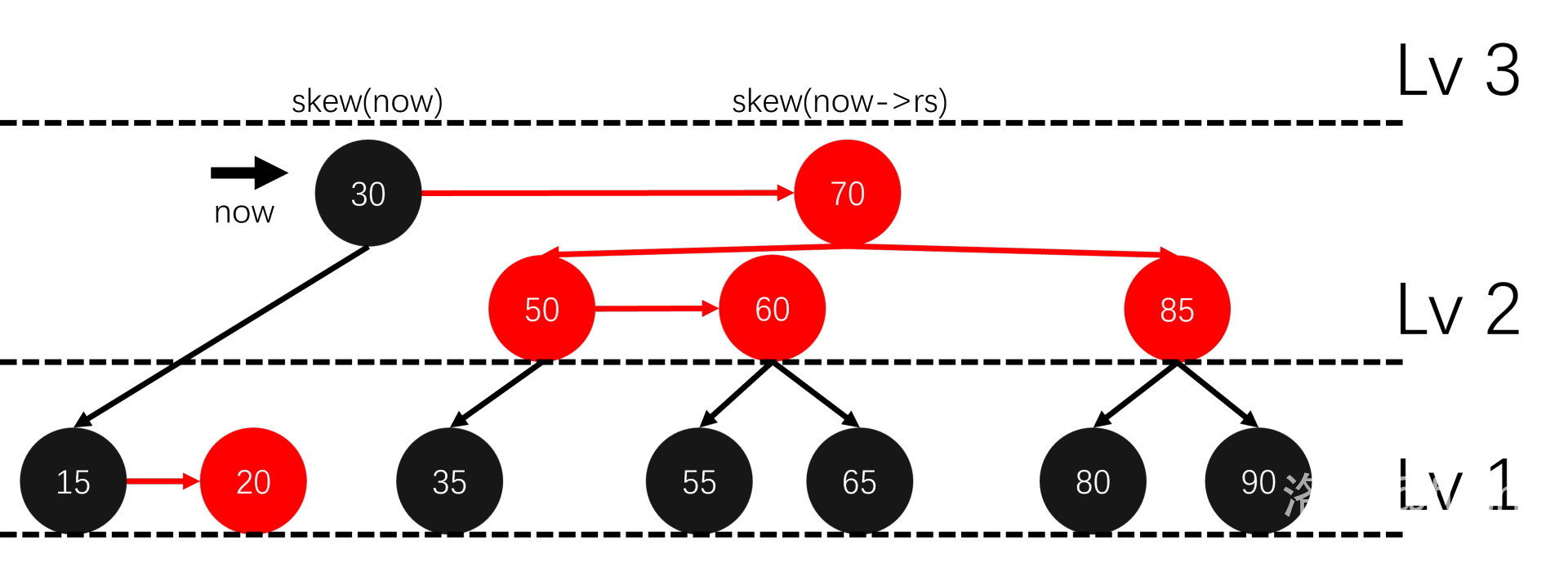
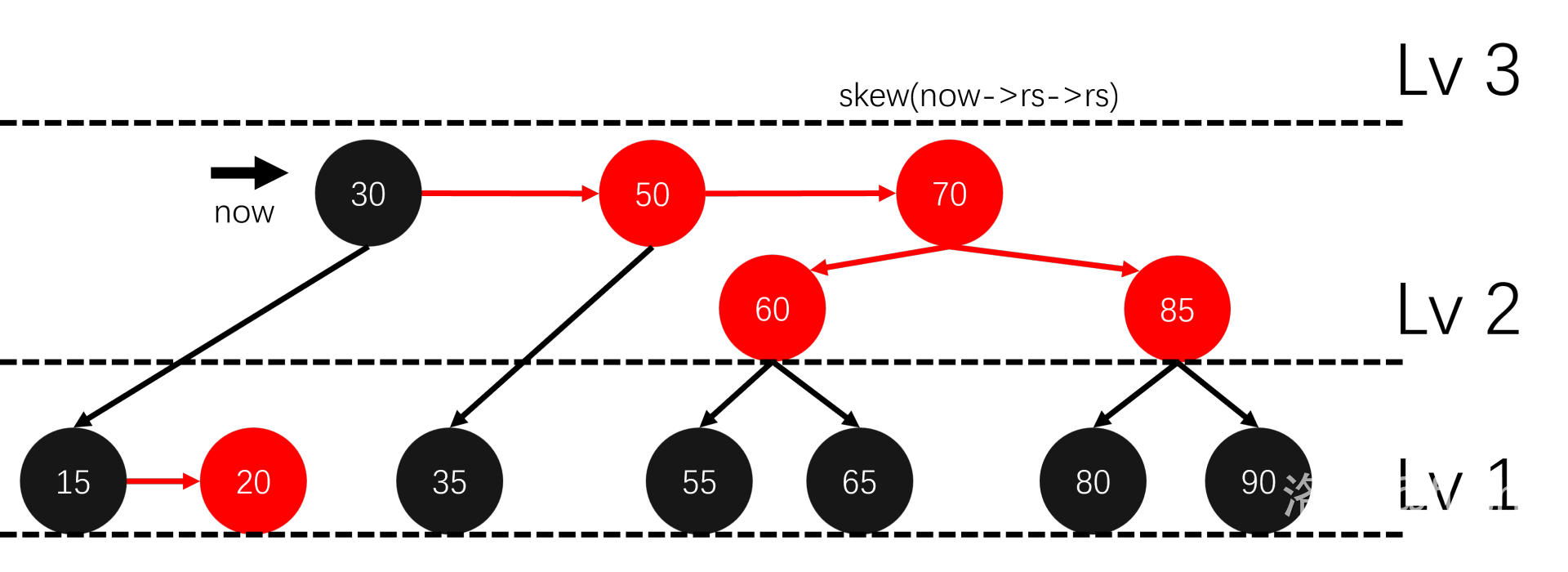
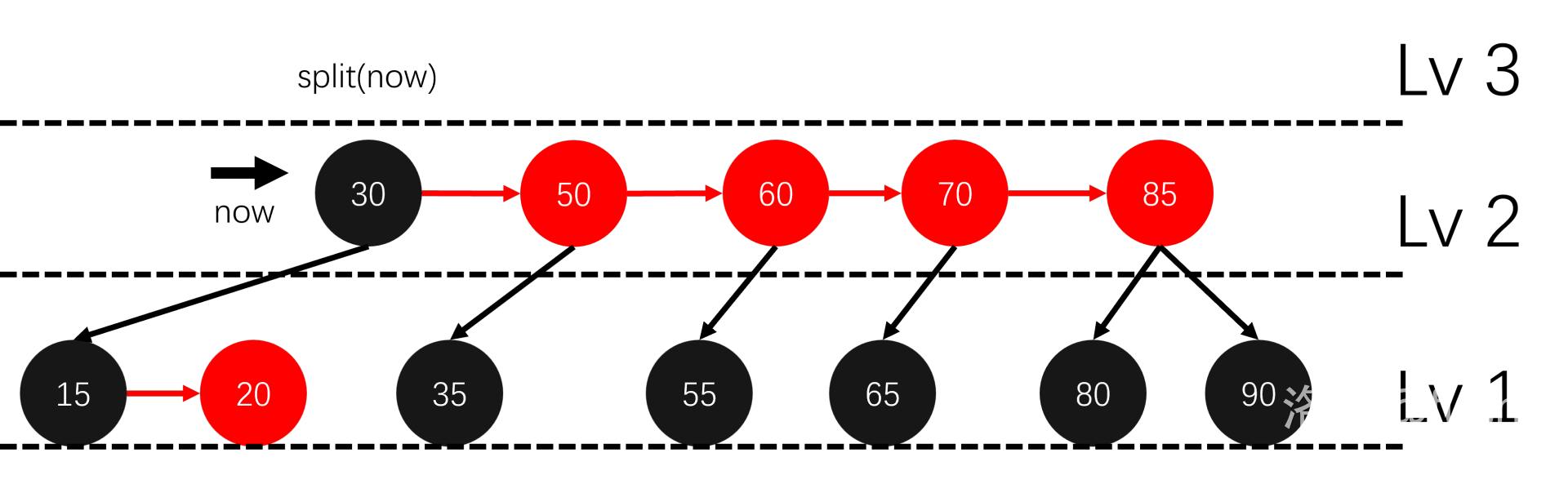
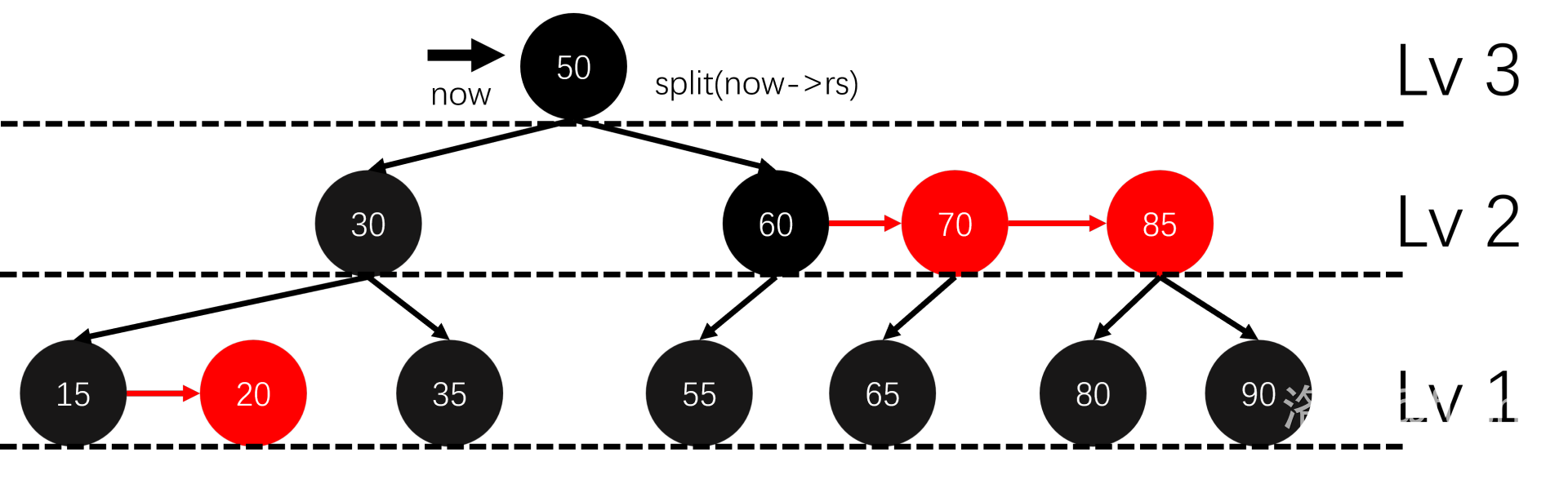
这样就修正好了,每层最多进行 \(3\) 次 skew 和 \(2\) 次 split,也不用太多的分类讨论。
void del(int &x, int val){
if(!x)return;
if(d[x].val == val){
int w = x;
if(d[w].ls && d[w].rs){//和后继交换
w = d[w].rs;
while(d[w].ls)w = d[w].ls;
d[x].val = d[w].val;
del(d[x].rs, d[w].val);
}
else x = d[x].ls ? d[x].ls : d[x].rs;
}
else if(d[x].val > val)del(d[x].ls, val);
else del(d[x].rs, val);
if(d[d[x].ls].lv < d[x].lv - 1 || d[d[x].rs].lv < d[x].lv - 1){
if(d[d[x].rs].lv > --d[x].lv)d[d[x].rs].lv = d[x].lv;//降级
skew(x), skew(d[x].rs), skew(d[d[x].rs].rs), split(x), split(d[x].rs);
}
if(x)pushup(x);
}