Splay初步

标签：初步 phi val fa int Splay zig now

更好的阅读体验？

前言

前置知识：

• 二叉搜索树

其实 Splay 的实现蛮多的，如果真的要能懂的话建议自己画图理解。
加油。

基础操作

准备操作

我们先把节点要维护的先定义出来。

子树大小	节点的权值	左儿子	右儿子	父亲
size	val	ch[0]	ch[1]	fa

struct node{int size, val, ch[2], fa;}d[N];
#define ls(x) d[x].ch[0]
#define rs(x) d[x].ch[1]
#define fa(x) d[x].fa

再定义几个基础函数：

int root, tot = 0, stk[N], top;
int newnode(int val){
    int w = top ? stk[top--] : ++tot;
    d[w].size = 1, d[w].val = val, ls(w) = rs(w) = fa(w) = 0;
    return w;
}
void pushup(int x){d[x].size = 1 + d[ls(x)].size + d[rs(x)].size;}
#define delnode(x) stk[++top] = x  //垃圾回收
bool get(int x){return x == rs(fa(x));} //是父亲的左/右儿子

旋转

rotate 操作的本质是把某个给定节点上移一个位置，并保证二叉搜索树的性质不改变。
在 Splay 中，旋转操作分为左旋（Zag）和右旋（Zig）（图上节点是编号）。

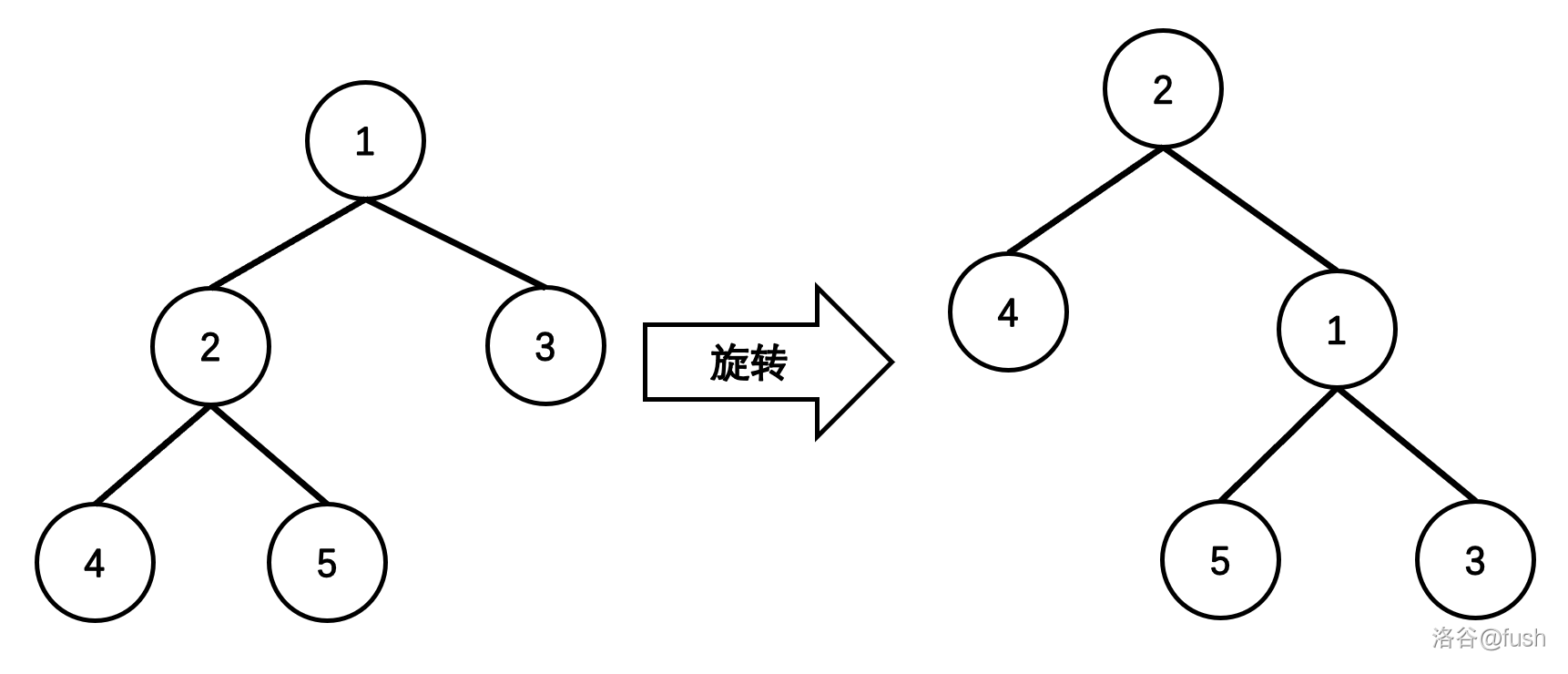
我们来模拟一下右旋的操作（红色是要删除的，蓝色是更改后的）。

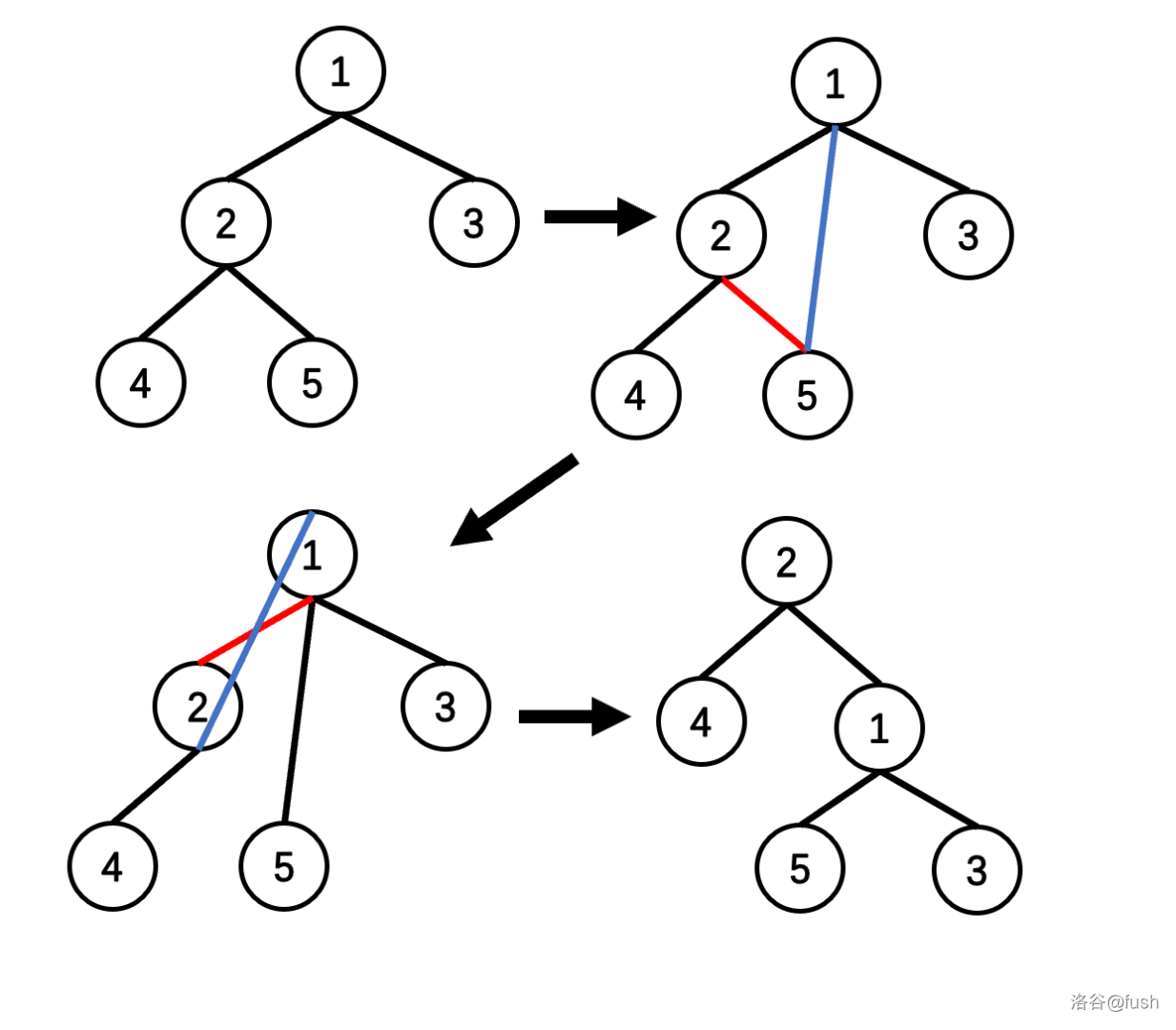
这样就完成了一次旋转。
而在实现中，我们会把 Zag 和 Zig 写在一起。
这里 rotate(x) 表示将 \(x\) 旋转到它父节点的位置。

void rotate(int x){
    int y = fa(x), z = fa(y), c = get(x);
    if(d[x].ch[!c])fa(d[x].ch[!c]) = y;// 把 x 相反方向的儿子接在 y 上。
    d[y].ch[c] = d[x].ch[!c], d[x].ch[!c] = y, fa(y) = x, fa(x) = z;
    if(z) d[z].ch[y == d[z].ch[1]] = x; //y 的父亲已经是 x 了。
    pushup(y), pushup(x);
}

splay

splay(x) 表示把 \(x\) 节点旋转到根节点。
我们可以简单分成 \(3\) 种：

zag/zig

很简单，对 \(x\) 做一次 rotate 即可（图就不放了）。

zag-zig/zig-zag

即 get(fa(x)) != get(x)。
对 \(x\) 做两次旋转即可。

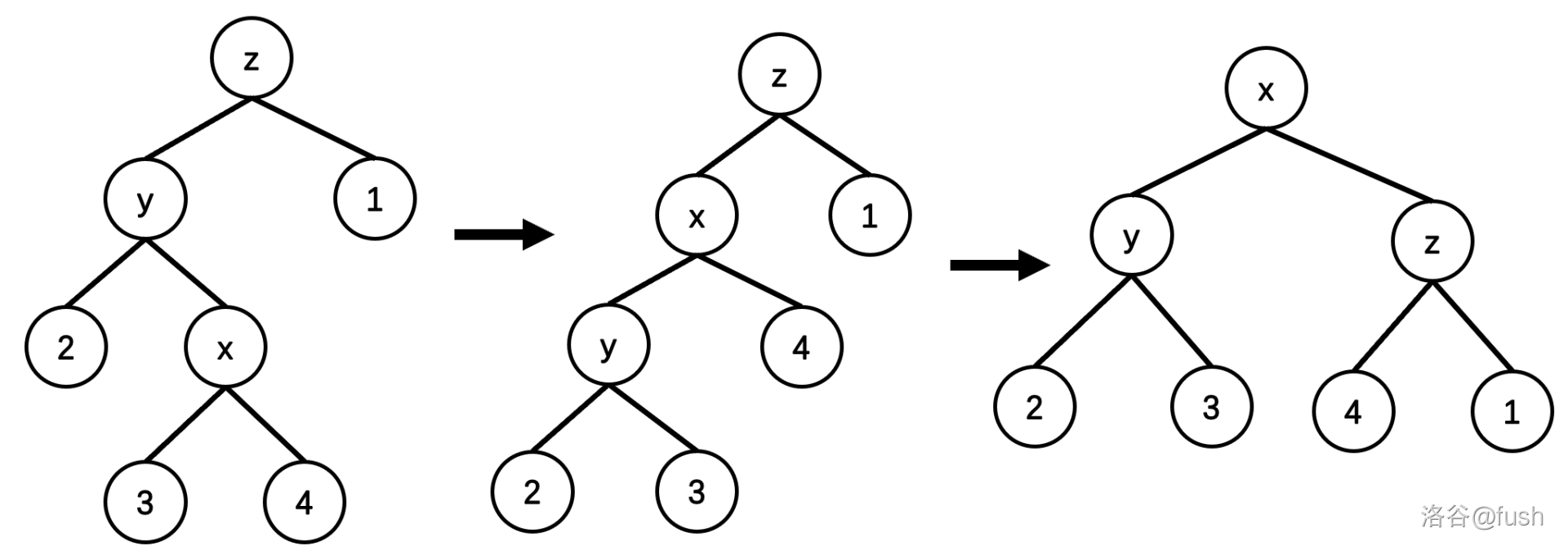
zag-zag/zig-zig

即 get(fa(x)) == get(x)，这个时候只旋转 \(x\) 是不对的。
我们要先旋转 fa(x) 再旋转 \(x\)，也就是双旋。

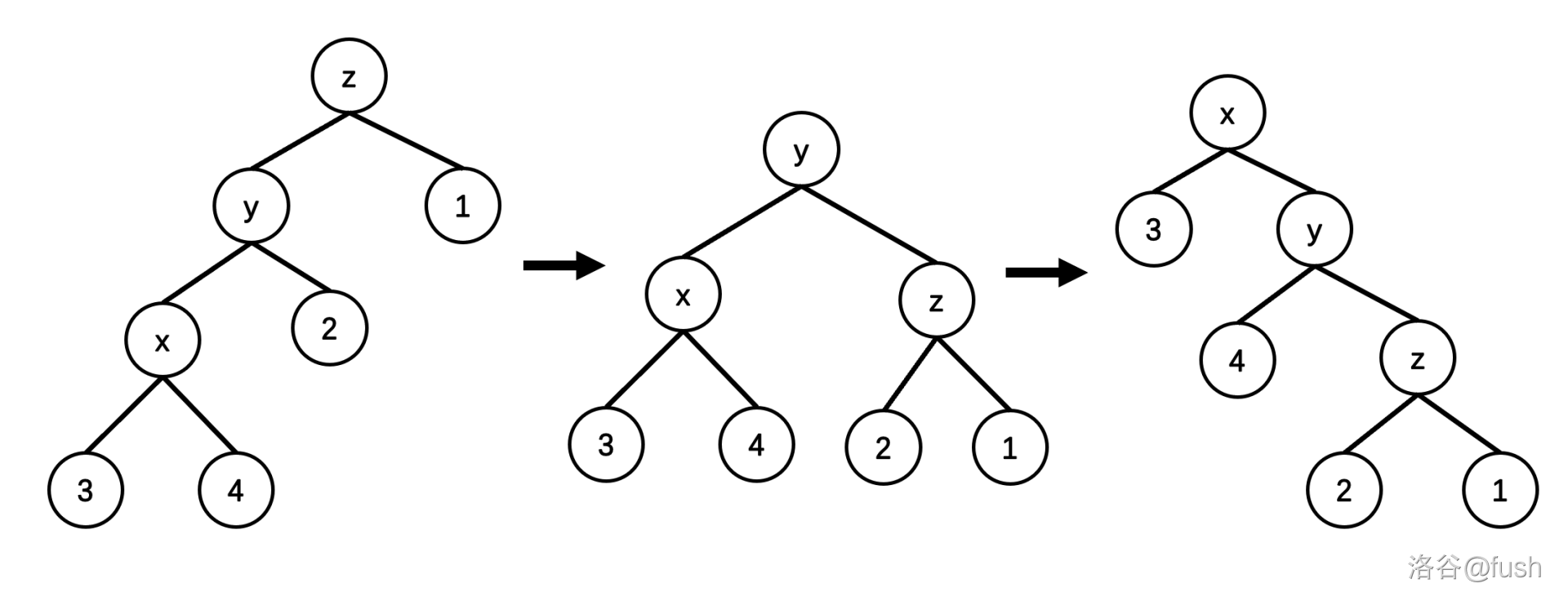
为什么我们要弄出双旋呢？

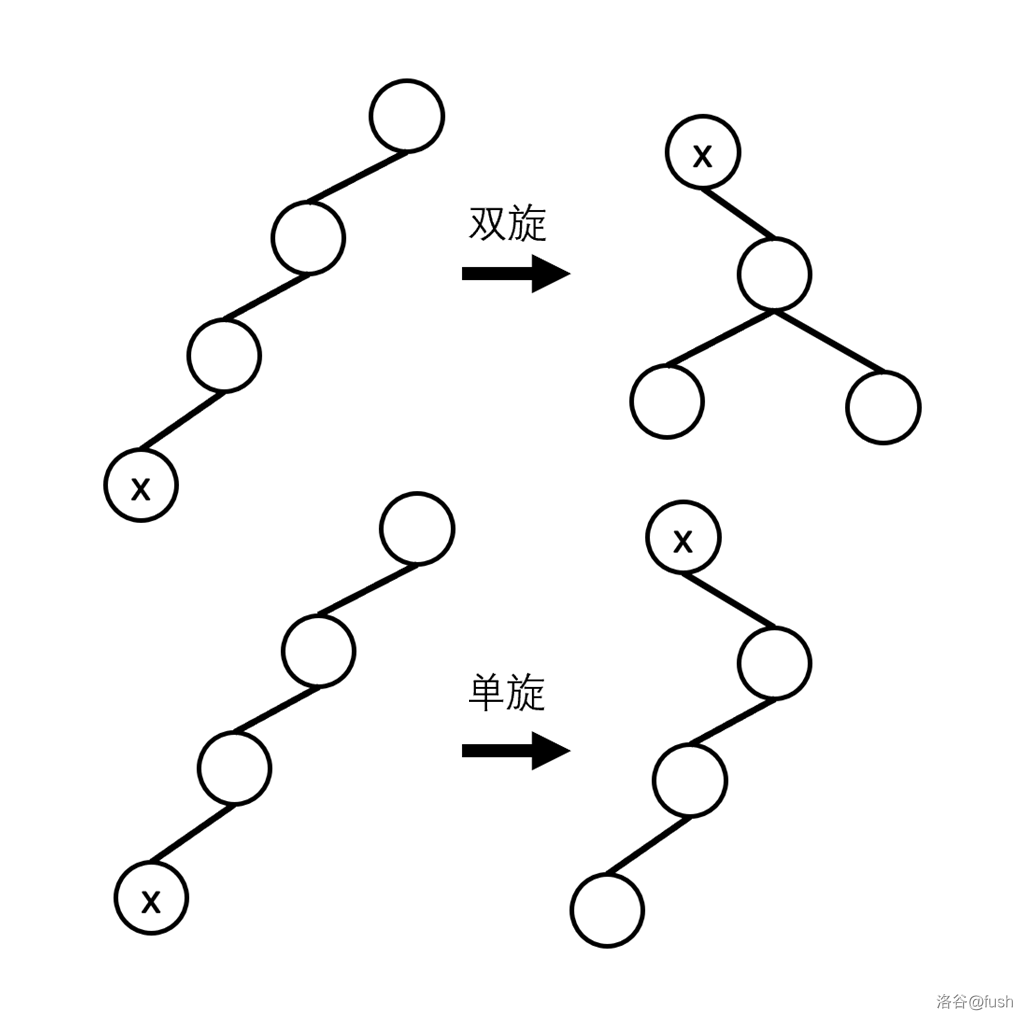
因为双旋会减少一层，明显会更优。

代码

void splay(int x){
    for(int f = fa(x); f = fa(x), f; rotate(x)) // 不论哪个操作，最后一步都是 rotate(x)
        if(fa(f))rotate(get(f) == get(x) ? f : x); // 判断转父亲还是转自己
    root = x;
}

时间复杂度

这段内容来自博客mr_spade。

为了方便描述，定义如下内容：
\(\qquad\)我们用 \(T\) 表示一棵完整的 Splay，并（不严谨地）用 \(\left|T\right|\) 表示 \(T\) 的节点数目。
\(\qquad\)如无特殊说明，小写英文字母（如 \(x\)，\(y\)，\(y\)）表示 \(T\) 的一个节点，\(x \in T\) 表示节点 \(x\) 在 \(T\) 中。
\(\qquad\)并（不严谨地）用 \(\left|x\right|\) 表示以节点为根的子树的大小。
\(\qquad\)我们默认 \(x'\) 代表节点 \(x\) 在经过了上下文中描述的操作以后的状态，因此对应的 \(x\) 代表之前的状态。
\(\qquad\)我们用 \(\Phi(T)\) 表示整棵 \(T\) 的势能函数，\(\phi(x)\) 则表示节点对 \(T\) 贡献的势能。

先来讲一下我们的势能函数，我们定义：

\[\phi(x) = \log \left|x\right|\\ \Phi(T) = \sum_{x \in T}\phi(x) \]

可以发现，对于任意时刻，因为 \(\left|x\right| \ge 1\)，因此 \(\phi(x) \ge 0\)，从而得到 \(\Phi(T) \ge 0\)，因此势能函数是合法的。
同时 \(\forall\left|x\right|\le\left|T\right|\)，因此我们总有 \(\phi(T) \le \left|T\right|\log\left|T\right|\)。这个上界是比较松的，但是对我们的分析没有影响。

下面考虑一次伸展操作对于势能函数的影响。

由于我们可以把从根向下查找的代价计算到伸展过程中对应的旋转操作上，此时旋转操作复杂度不变，只是常数增大，从而忽略了查找对复杂度的影响。
我们可以简单地通过增大势的单位来支配隐藏在操作中的常数。
因此我们只需证明对于一次伸展操作的所有旋转操作，其复杂度是均摊 \(\log \left|T\right|\) 的，我们就完成了对 Splay 复杂度的证明。

zig/zag

由于 zig 操作与 zag 相似，因此只需要证明 zig 即可。

假设我们 zig 的对象是 \(x\)，其父亲为 \(y\)，显然在旋转以后，只有 \(x\) 和 \(y\) 的子树大小发生了变化。
因此势能变化量为：

\[\Delta\Phi(T) = \phi(x') +\phi(y') - \phi(x) - \phi(y) \]

显然 \(\phi(x') = \phi(y)\)，且 \(\phi(x')\ge\phi(y')\)，因此消去 \(\phi(x')\) 与 \(\phi(y)\)，并将 \(\phi(y')\) 替换为 \(\phi(x')\)，有：

\[\Delta\Phi(T) \le \phi(x') - \phi(x) \]

因此 zig 操作的均摊代价为 \(O(1 + \phi(x') - \phi(x))\)，其中 \(O(1)\) 代表旋转操作本身的复杂度。
而在一次伸展操作中也只会有一次 zig 操作，因此这额外的 \(O(1)\) 代价不会对分析造成影响，因此我们可以只关心其中的 \(O(\phi(x') - \phi(x))\)。

zig-zig/zag-zag

由于 zag-zag 操作与 zig-zig 相似，因此只需要证明 zig-zig 即可。

假设我们 zig-zig 的对象是 \(x\)，其父亲为 \(y\)，其祖父为 \(z\)，与 zig 操作类似，势能变化量为：

\[\Delta\Phi(T) = \phi(x') + \phi(y') + \phi(z') - \phi(x) - \phi(y) - \phi(z) \]

同样地，由于 \(\phi(x') = \phi(z)\)，因此将它们消去：

\[\Delta\phi(T) = \phi(y') + \phi(z') - \phi(x) - \phi(y) \]

而我们又有 \(\phi(x') \ge \phi(y'), \phi(x) \le \phi(y)\)，因此有：

\[\Delta\Phi(T) \le \phi(x') + \phi(z') - 2\phi(x) \]

推到这里，我们先来做一个小工作，来证明 \(\phi(x) + \phi(z') - 2\phi(x')\)（注意与上面的式子不一样）的值不大于 \(-1\)。

假设 \(\left|x\right| = a, \left|z'\right| = b\)，那么我们有：

\[\phi(x) + \phi(z') - 2\phi(x') = \log\left|x\right|+\log\left|z'\right| - 2\log\left|x'\right| \]

我们将 \(\log\) 合并，得到：

\[\phi(x) + \phi(z') - 2\phi(x') = \log(\dfrac{\left|x\right|\left|z'\right|}{\left|x'\right|^2}) \]

由于 \(\left|x'\right|\ge a+ b\)（可以结合旋转过程思考一下），而 \(\log\) 是单调的，因此：

\[\phi(x) + \phi(z') - 2\phi(x') \le \log(\dfrac{ab}{(a + b)^2}) \le \log(\dfrac{ab}{2ab}) \le -1 \]

证明完毕。
现在我们已经知道 zig-zig 操作的摊还代价不大于：

\[O(1) + \phi(x') + \phi(z') - 2\phi(x) \]

其中 \(O(1)\) 为旋转操作的复杂度。由于之前的推导我们可以知道 \(\phi(x)+\phi(z')-2\phi(x')\le-1\)，因此 \(-1-(\phi(x)+\phi(z')-2\phi(x'))\ge 0\)，我们在摊还代价上加上这个非负数得到：

\[O(1) + \phi(x') + \phi(z') - 2\phi(x) - 1-(\phi(x)+\phi(z') - 2\phi(x')) \]

化简一下，就得到：

\[O(1) + O(\phi(x') - \phi(x)) - 1 \]

通过增大我们刚刚加的那个非负数以及势的单位，我们就可以支配隐藏在 \(O(1)\) 中的常数，因此一次 zig-zig 操作的摊还代价为：

\[O(\phi(x') - \phi(x)) \]

zig-zag/zag-zig

分析的过程和 zig-zig 操作完全一样，之前分析用到的所有性质此时仍然适用，因此略过分析过程。其摊还代价依然为：

\[O(\phi(x') - \phi(x)) \]

综上所述，除了最后一次旋转可能增加 \(O(1)\) 的代价以外。
其余操作的摊还代价只和我们伸展的对象 \(x\) 的势能有关。
我们假设旋转操作一共执行了 \(n\) 次，并用 \(x_i\) 来表示节点 \(x\) 在经过 \(i\) 次旋转后的状态，那么整一个伸展操作的摊还代价就为：

\[O(1 + \sum_{i = 1} ^n\phi(x_i) - \phi(x_{i - 1})) \]

显然除了 \(\phi(x_n)\) 与 \(\phi(x_0)\) 外，所有的势能都被抵消了，因此摊还代价为：

\[O(1 + \phi(x_n) - \phi(x_0)) \]

至此，我们不必关心 \(\phi(x_0)\) 的值了。
此时 \(\phi(x_n)\) 是 \(T\) 的根，因此 \(\phi(x_n) = \log\left|T\right|\)。
我们成功的证明了一次伸展操作的摊还代价为 \(\log \left|T\right|\)。
所以是均摊 \(O(\log n)\)。

其他操作

剩下的操作就和普通的二叉搜索树区别不大了，记得做完后 splay。

插入

void insert(int val){
    int now = root, f = 0;
    while(now) f = now, now = d[now].ch[val > d[now].val];
    now = newnode(val), fa(now) = f, d[f].ch[val > d[f].val] = now, splay(now);
}

删除

删除真的挺麻烦的，在大部分的平衡树中都是除平衡操作外最长的。

void del(int val){
    int now = root, f = 0;
    while(d[now].val != val && now)f = now, now = d[now].ch[val > d[now].val];
    if(!now)return splay(f); // 不存在
    splay(now);
    int cur = ls(now);
    if(!cur)return root = rs(now), fa(rs(now)) = 0, delnode(now), void();//没有左儿子
    while(rs(cur)) cur = rs(cur);
    rs(cur) = rs(now), fa(rs(now)) = cur, fa(ls(now)) = 0, delnode(now); //把右儿子接在左子树的最大权值下面
    pushup(cur), splay(cur);
}

查排名

平衡树内可能有好几个权值为 \(val\) 的节点，但我们要找的是严格小于的。

int query_rank(int val){
    int ans = 1, now = root, f;
    while(now)
        if(d[f = now].val < val)ans += d[ls(now)].size + 1, now = rs(now);
        else now = ls(now);
    return splay(f), ans;
}

查询第 k 小

根据 \(size\) 判断走哪边即可。

int kth(int rak){
    int now = root, siz;
    while(now){
        if((siz = d[ls(now)].size + 1) > rak) now = ls(now);
        else if(!(rak -= siz)) break;
        else now = rs(now);
    }
    return splay(now), d[now].val;
}

前驱

一种简单的写法：
先插入一个 \(x\)，这样 \(x\) 就是根了。
那 \(x\) 的前驱，就是先走根的左儿子，然后再一直走右儿子走到底。最后再删掉插入的这个 \(x\)。
但原本写了删除、插入还好，如果没有，还要单独写。

我们换一种写法：
若 \(val_{now} \ge val\)，说明答案在 \(now\) 的左子树，\(now \gets ls_{now}\)。
否则，我们记录一下，然后走进右子树，\(ans \gets val_{now}, now \gets rs_{now}\)。

int ask_pre(int val){
    int now = root, ans = -1e9, f;
    while(now)
        if(d[f = now].val >= val)now = ls(now);
        else ans = d[now].val, now = rs(now);
    return splay(f), ans;
}

后继

跟前驱差不多，反一下就好了。

int ask_next(int val){
    int now = root, ans = 0, f;
    while(now)
        if(d[f = now].val <= val)now = rs(now);
        else ans = d[now].val, now = ls(now);
    return splay(f),ans;
}

完整代码

洛谷普通平衡树。

序列操作

我们可以不在关心每个节点之间的大小关系。
我们让树的中序遍历的结果变成序列上的顺序。

splay 操作

假设我们要操作 \([l, r]\) 的区间，我们需要让树变成这样：

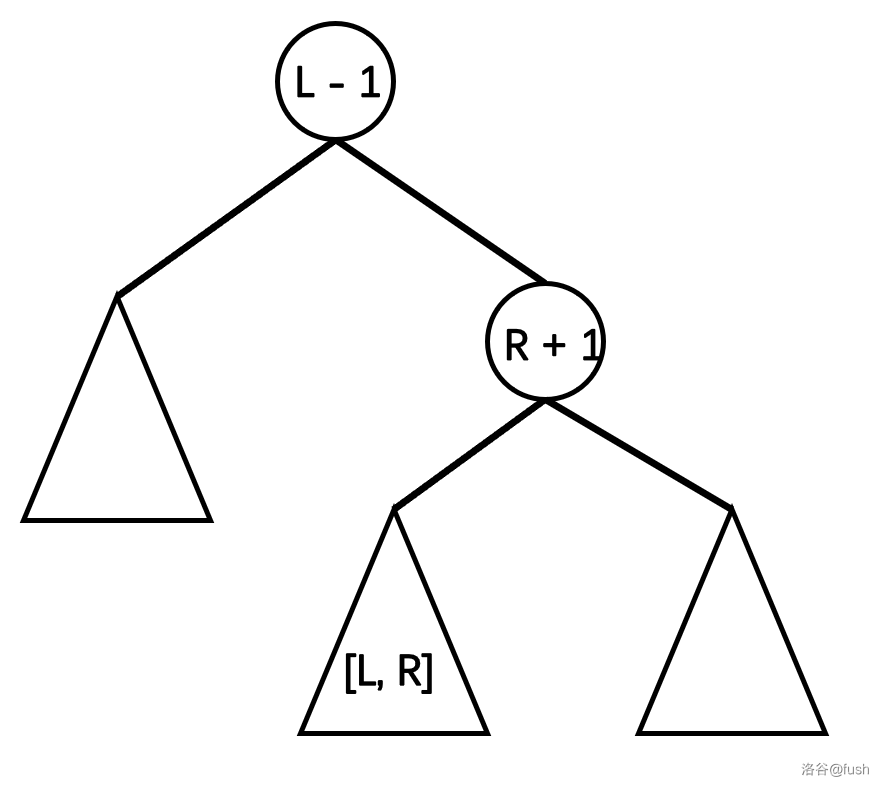
如果直接使用之前的 splay 操作的话明显不好实现，所以我们要更改一下。
把旋转到根节点改为，旋转到 \(p\) 节点的儿子节点。

void splay(int x, int p){
    for(int f = fa(x); f = fa(x), (f ^ p); rotate(x))
        if(fa(f) ^ p)rotate(get(f) == get(x) ? f : x); 
    if(!p)root = x;
}

使用更改后的 splay 就可以比较方便的实现了。
先将 \(l - 1\) 节点旋转至根节点，然后在右子树内找到 \(r + 1\) 节点，旋转到 \(l - 1\) 的儿子。
为了防止 \(l = 1\)、\(r = n\) 的情况，我们可以先加入 \(0\) 和 \(n + 1\) 两个虚点，注意不要输出了。

find

和之前的 kth 区别不大，但因为虚点，所以要将排名 \(+1\)，也不用 splay 了。

int find(int k){
    int now = root, siz;k++;
    while(now){
        pushdown(now);
        if((siz = d[ls(now)].size + 1) > k) now = ls(now);
        else if(!(k -= siz)) break;
        else now = rs(now);
    }
    return d[now].val;
}

输出

别把虚点输出了。

void print(int now){
    pushdown(now);
    if(ls(now)) print(ls(now));
    if(d[now].val) cout << d[now].val << " ";
    if(rs(now)) print(rs(now));
}

完整代码

洛谷文艺平衡树。
洛谷维护数列。

标签：初步,phi,val,fa,int,Splay,zig,now
From： https://www.cnblogs.com/fush/p/18639443