香港大学 CS 笔试真题（三）

前言

本文章主要内容为笔试当中的数学真题，涉及高等数学、线性代数、概率论与数理统计的基础知识以及其他数学理论。

注：部分纯计算题目暂只给出题目，推荐参考网课为宋浩老师的 B 站课程。

一、高等数学

01 连续性函数

A monk climbs a mountain. He starts at 8am and reaches the summit at noon. He spends the night on the summit. The next morning, he leaves the summit at 8am and descends by the same route that he used the day before, reaching the bottom at noon. Argue that there is a time between 8am and noon at which the monk was at exactly the same spot on the mountain on both days.

Solution:

This conclusion can also be visualized: if we draw the monk's path on both days on the same graph, the curve representing the ascent will intersect with the curve representing the descent, confirming that there is a common point in time.

02 Ramsey定理

请你证明，在6个人中，或者有3个人，他们中的每两个人都互相认识，或者有3个人，他们中的每两个人都彼此不认识。

解:

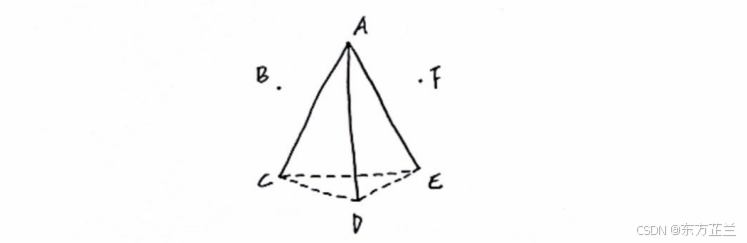
不管用红色和蓝色如何去着色K6的边，总存在一个红K3（原始的6个点中有3个，点，它们之间的3条线段均被画成红色）或蓝K3（原始的6个点中有个点，它们之间的3条线段均被画成蓝色），简言之，总存在一个单色三角形。

03 数学归纳

请你证明，序列对所有正整数n都成立。

Solution:

04 求导与积分

xsinx 求导

5x^4+lnx 求导

x/(1+x) 求不定积分

(1/x)+4e^(2x) 求不定积分

二、线性代数

01 矩阵变换

Consider the following two tables. Argue that we cannot transform the left table into the right table by exchanging its rows and columns?

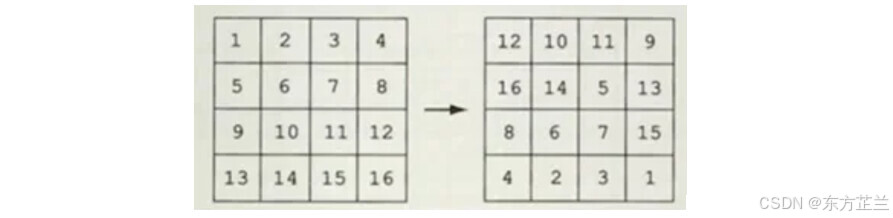
Solution:

Regardless of how we perform row or column exchanges, the numbers in each row remain constant. For instance, the row containing 5, 6, 7, and 8 will always consist of those same numbers, regardless of their position. However, in the right table, we see that those numbers change to 8, 6, 7, and 15. This indicates that it is impossible to convert the left table into the right table solely through row and column exchanges.

02 部分概念

矩阵逆、标准差、单位矩阵

三、概率论与数理统计

01 条件概率

2）In probability theory and statistics, the Bayes' theorem relates the conditional probability that P(A|B) , the probability that A is true given that B is true by the following probabilities:

P(A): probability that A is true.

P(B): probability that B is true.

P(B|A): probability that B is true given that A is true.

State the Bayes' theorem (express P(A|B) in terms of the above three probabilities).

3）两对夫妻各生了一个小孩，其中一个是女孩，求另一个也是女孩的概率。

4）从一个数组里拿两个数，其中一个数是 2，求两个数的和大于 6 的概率。

5）两个七面骰子各骰一次，求它们和的所有可能个数的条件概率公式，不考虑顺序。

6）三个普通骰子各骰一次，求一共多少种组合，不考虑顺序。

7）抛五枚硬币，其中至少有 2 枚硬币正面朝上，求恰好有 3 枚硬币正面朝上的概率。

02 全概率

A bag contains 4 balls. Two balls are drawn at random without replacement and are found to be blue. What is the probability that all balls in the bag are blue?

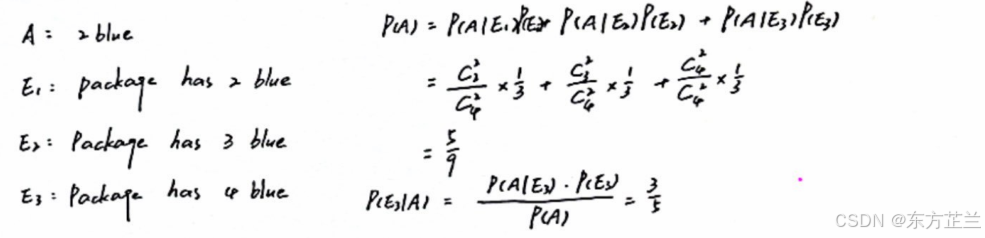
03 期望与方差

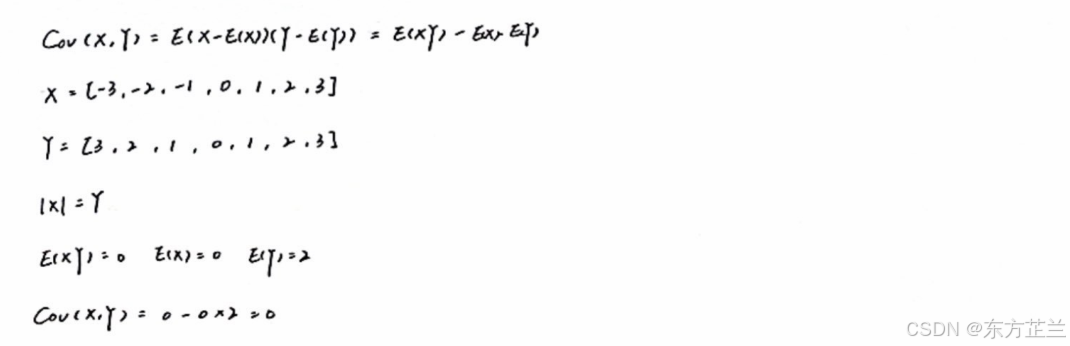
2）从 1~20 中挑选一个整数，抽到偶数的概率是 0.7，抽到奇数的概率是 0.3，当抽到奇数 n 时，损失 n 美元，当抽到偶数 n 时，赚到 n 美元。例如抽到 3，则损失 3 美元，抽到 6，则赚到 6 美元，求最终钱的期望值。

04 相互独立

1）已知事件 A 为一个家庭有3个孩子，其中有男孩，事件 B 为这个家庭最多有一个男孩，请判断事件 A 和事件 B 是否相互独立。

2）如果事件 A 和事件 B 相互独立，则 P(A) 和 P(B) 满足什么关系。

05 古典概型

2）一副标准的扑克牌中抽出 5 张牌，求有 3 个 A 的概率和没有黑桃的概率。

3）一个人面试三个职位，这三个职位的候选人分别是2，3和4个，每个人获得职位的概率相等，求这个人没有拿到任何职位的概率。

4）五个人围成一圈，求选定的两个人刚好相邻的概率。