在研究X对Y的影响时,因变量Y有时是分类变量,这时如果还想分析影响关系可以使用logit回归,常见的logit回归包括,二元logit回归(二项logit回归)、多分类logit回归以及有序logit回归。三者的区别如下:
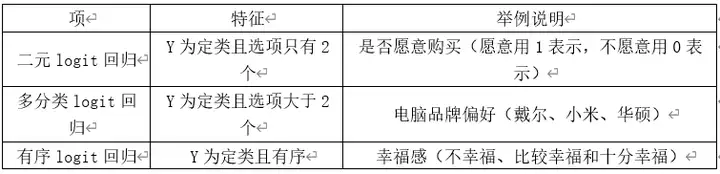
此案例使用多分类logit回归研究幸福感情况。
一、案例背景
某研究者分别于1985年、1995年、2005年调查了已婚及未婚的30岁左右成年人的幸福感情况,部分数据如下,有时“幸福感”也会看成是有序变量,如果看成有序变量,该案例可以进行“有序logit”,该案例将“幸福感”看成多分类变量。所以用多分类logit分析。
该研究以“幸福感”为因变量,“婚姻状况”和“年份”为自变量建立模型,观察模型影响因素
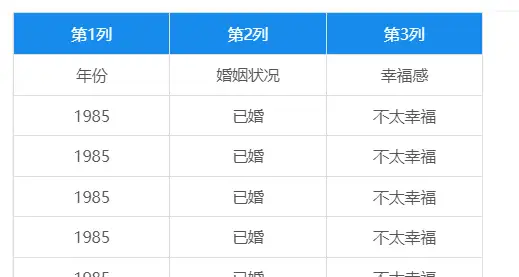
二、分析前处理
对于自变量,该案例认为“婚姻状况”、“年份”为定类变量所以将二者进行哑变量处理。
补充说明:
多分类logit因变量为类别数据,研究X对Y的影响时,如果为类别数据,那么不能说越如何越如何,这就是类别数据的特点,一定是相对某某而言。这就导致了多分类logistic回归分析时,文字分析的难度加大,如果说因变量Y的类别个数很多,比如为10个,此时建议时对类别进行组合下,尽量少的减少类别数量,便于后续进行分析。此步骤可通过SPSSAU数据处理模块的数据编码功能完成。该案例的类别只有三个所以不进行处理。
三、结果分析
结果将从四个方面进行说明,其中包括“基本汇总”、“模型似然比检验”、“模型公式及影响关系”以及“模型预测效果分析”。
- 基本汇总
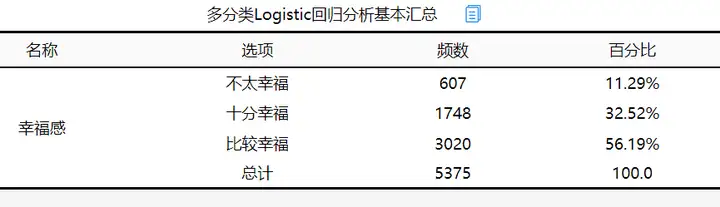 分析结果来源于SPSSAU
分析结果来源于SPSSAU
从上表可以看出共有5375个样本参与分析,其中比较幸福的成年人占比较大,占总分析人数的56.19%,不太幸福的成年人占比最少,占总分析人数的11.29%,接下来对模型似然比检验进行查看。
- 模型似然比检验

首先对p值进行分析,如果该值小于0.05,则说明模型有效;反之则说明模型无效,从上表可以看出p值小于0.05,说明拒绝原定假设,即说明本次构建模型时,放入的自变量具有有效性,本次模型构建有意义。接下来构建模型以及分析影响因素。
- 模型公式及影响关系
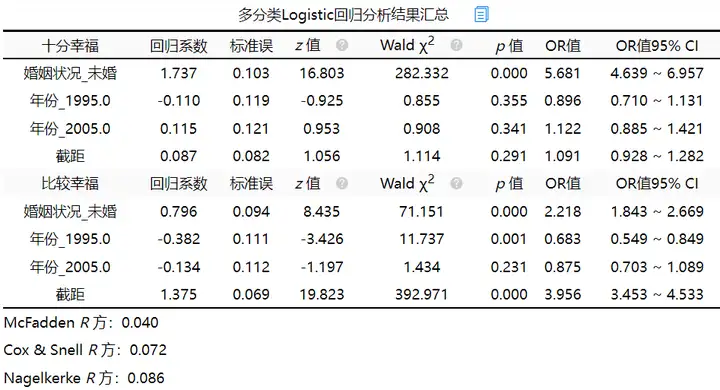
该案例的参考项是“不太幸福”,并且因为对自变量婚姻情况和年份进行哑变量处理,所以放入的自变量分别为‘婚姻状况_未婚’‘年份_1995年’以及‘年份_2005年’。有上表可以得到模型公式。
说明如下:
ln(十分幸福/不太幸福)=0.087 + 1.737*婚姻状况_未婚-0.110*年份_1995.0 + 0.115*年份_2005.0
ln(比较幸福/不太幸福)=1.375 + 0.796*婚姻状况_未婚-0.382*年份_1995.0-0.134*年份_2005.0
影响关系具体分析如下:
(1)“十分幸福”和“不太幸福”进行比较
相对于不太幸福来讲,在十分幸福的前提之下,婚姻情况为未婚的回归系数为正并且p值<0.05,未婚会对幸福感产生显著的正向影响关系。也就是相对于“幸福感”来讲,未婚成年人比已婚成年人会幸福。
(2)“比较幸福”和“不太幸福”进行比较
相对于不太幸福来讲,在比较幸福的前提之下,婚姻情况为未婚的回归系数为正并且p值<0.05,所以未婚会对幸福感产生显著的正向影响关系。也就是相对于“幸福感”来讲,未婚成年人比已婚成年人比较幸福。并且分析项1995年的p值<0.05并且回归系数为-0.382<0,所以相对于1985年调查的成年人不太幸福。
- 模型预测效果分析
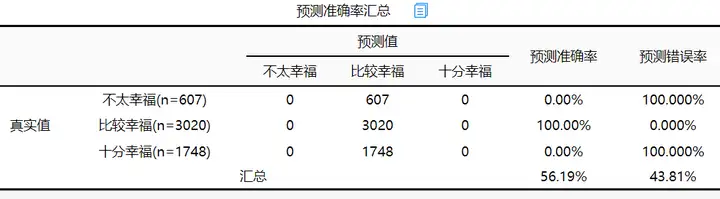
通过模型预测准确率去判断模型拟合质量,从上表可知:研究模型的整体预测准确率为56.19 %,模型拟合情况一般。该案例分析模型预测不是重点,如正常分析可以忽略。
四、总结
案例利用多分类logit回归分析方法,以“幸福感”为因变量,“婚姻状况”和“年份”为自变量建立模型,观察模型影响因素。在分析前对自变量进行处理以及对结果进行分析,其中包括基本汇总、模型似然比检验、模型公式及影响关系以及模型预测效果分析,该案例分析模型预测不是重点,如正常分析可以忽略。最后发现就是相对于“幸福感”来讲,未婚成年人比已婚成年人会幸福。1985年调查成年人比1995年调查的成年人更幸福。
标签:logit,分析,年份,幸福,回归,案例,模型 From: https://www.cnblogs.com/spssau/p/16843558.html