R统计 | 简单探索性数据分析（一）：缺失值的处理

R统计 | 简单探索性数据分析（一）：缺失值的处理

    本系列内容主要聚焦于数据分析前的探索部分，具体涵盖缺失值的处理、统计量的描述、数据分布特征的检验以及数据关联性的初步探索。本系列内容的概念部分源自ChatGPT3.5，实战部分基于小编理解，参考公众号庄闪闪的R语言手册、生态R学社、医学和生信笔记、R语言和统计、R语言统计与绘图，进行适合土壤生态学研究内容的改写与总结。参考部分均有标注，改写部分如有错误还请海涵。

什么是探索性数据分析？

探索性数据分析（Exploratory Data Analysis，简称EDA）是数据分析的一种方法，旨在通过可视化和统计方法来探索数据集，以发现数据中的模式、趋势、异常和关联关系，以及提取有关数据的初步见解。EDA的目标是理解数据的结构和特征，而不是进行具体的假设测试或建立模型。

探索性数据分析通常包括以下主要步骤：

1. 缺失值处理： 检查并处理数据中的缺失值，确保在分析过程中不会因缺失数据而产生误导性的结果。
2. 总结统计量： 对数据集进行基本的统计描述，包括平均值、中位数、标准差、最小值和最大值等，以获取关于数据集整体性质的信息。
3. 可视化： 利用图表、图形和图像来呈现数据，以更直观地理解数据的分布和关系。常用的可视化工具包括散点图、直方图、箱线图等。
4. 发现模式： 寻找数据中的模式、趋势或周期性变化，以便更好地理解数据的内在结构。
5. 异常值检测： 检查数据中是否存在异常值或离群点，这有助于识别数据集中的不寻常行为或可能的错误。
6. 关联分析： 探索数据中变量之间的关系，例如相关性和因果关系，以帮助理解变量之间的相互作用。

EDA是数据科学和统计学中的重要步骤，它能够帮助分析人员在进一步建模或进行深入分析之前对数据有更全面的认识。通过EDA，分析人员能够从数据中获得直观的感觉，为后续分析和决策提供有力支持。

缺失值的类型有哪些？

缺失值的类型主要可以分为以下几类：

1. 完全随机缺失 (MCAR - Missing Completely at Random): 缺失值的出现是完全随机的，不受任何其他变量的影响。在这种情况下，缺失的概率与观测值的其他信息无关。这种缺失的情况通常可以通过删除缺失值或使用随机插补方法来处理。

2. 随机缺失 (MAR - Missing at Random): 缺失的概率可能与观测值的其他已知变量相关，但与缺失值本身无关。在这种情况下，通过考虑其他已知变量的信息，可以使用各种插补方法来填充缺失值。

3. 非随机缺失 (MNAR - Missing Not at Random): 缺失值的出现与缺失值本身的未观测信息有关，无法通过已知变量来解释。这种类型的缺失是最为复杂和困难处理的，因为缺失的模式与数据的性质有关，可能导致结果的偏差。处理非随机缺失通常需要更复杂的模型和方法，如多重插补或模型预测填充。

为什么会存在缺失值？

生态学实验过程中，缺失值可能由多种原因产生，了解这些原因对于有效处理和解释数据至关重要。以下是一些常见的导致缺失值的原因以及该缺失值一般所属类型：

1. 设备故障： 在生态学实验中使用的测量设备，如传感器、记录器或监测设备，可能由于故障而导致数据丢失。属于随机缺失（MCAR），因为设备故障通常是随机发生的，不受其他变量的影响。
2. 人为错误： 人为因素，如数据输入错误、采样错误或记录错误，可能导致数据的缺失。一般是随机缺失（MCAR）或者是非随机缺失（MNAR），具体取决于错误的发生是否与其他变量相关。
3. 采样困难： 在一些生态系统中，采样可能因为环境条件、地形或生物学因素而变得困难，导致部分数据无法获取。通常可以归类为非随机缺失（MNAR），因为采样的困难可能与未观测的环境或地形特征相关。
4. 生物样本问题： 在采集生物样本时，可能会发生损失、污染或样本质量问题，导致相应的数据无效或丢失，一般是随机缺失（MCAR）。
5. 自然灾害： 突发的自然灾害，如风暴、火灾、洪水等，可能导致设备受损、采样地点受到影响，进而导致数据丢失，一般是随机缺失（MCAR）。
6. 动植物行为： 在生态学实验中，研究对象的行为可能导致数据的丢失。例如，动物可能在实验期间迁移、逃逸或发生其他不可预测的行为，使得观测或采样无法完成。一般是非随机缺失（MNAR），因为行为可能与未观测的生物学特征相关。
7. 数据传输问题： 当数据从采集点传输到存储或分析地点时，可能由于传输中的问题（如通信故障或数据损坏）而导致数据丢失，属于随机缺失（MCAR）。
8. 实验设计限制： 实验设计中的一些限制，如样本量的规模、实验的时长或资源的限制，可能导致无法获取完整的数据集。一般是非随机缺失（MNAR），因为这种类型的限制通常与未观测的实验条件或资源限制相关。

缺失值的存在会有什么影响?

缺失值在数据分析中可能引起多方面的负面作用，对研究结论和解释产生重要的影响。以下是一些主要的负面作用：

1. 失真数据的完整性： 缺失值会导致数据集的不完整，使得分析结果缺乏全面性。由于缺失数据的存在，可能无法全面了解研究对象或现象，从而影响对整体情况的准确理解。
2. 影响统计推断的准确性： 缺失值的存在可能导致样本量减少，从而影响统计推断的准确性和可信度。在许多情况下，样本量的减少可能使得检测到的效应不够显著，降低了分析的统计功效。
3. 引入选择偏差： 缺失数据的模式可能是非随机的，即缺失值可能与其他变量相关。如果忽略缺失值或仅仅删除缺失值，可能引入选择偏差，使得样本不再代表总体，从而影响分析的外推能力。
4. 降低模型预测的准确性： 对于涉及机器学习或统计模型的分析，缺失值可能导致模型训练不充分，影响对未知数据的准确预测能力。模型训练过程中，缺失值需要被处理以避免对模型性能的负面影响。
5. 影响变量关系的解释： 缺失值可能导致在变量之间的关系上产生误导。由于缺失数据的存在，可能无法全面了解变量之间的真实关系，从而影响对生态系统或生物群体的真实动态的解释。

如何进行缺失值处理?

• 删除缺失值： 如果缺失值数量较少且随机分布，删除缺失值可能是一个简单的解决方案。但是，这可能导致样本量减少，需要谨慎使用。

• 插值方法： 使用插值方法填补缺失值，例如线性插值、多项式插值或基于邻近点的插值。这可以帮助保持样本量，但要注意插值的适用性和可能引入的误差。

• 均值、中值、众数填充： 对于数值型变量，可以用均值、中值或众数填充缺失值。这对于保持整体分布的一致性可能是一个简单有效的方法。

• 模型预测填充： 利用其他变量构建模型，通过预测缺失值进行填充。这种方法可能更复杂，但可以更好地利用其他可用信息。

• 多重插补： 利用多个变量的信息，通过多次模型迭代来填充缺失值，以更好地反映数据的不确定性。

• 机器学习方法： 使用机器学习算法来预测缺失值，例如决策树、随机森林、或深度学习模型。

实验数据中的R实战

下面主要介绍生态学探索性数据分析中，常用的缺失值处理方法的R实现。

基于R自带鸢尾花数据集构建模拟缺失值数据集

library(tidyverse)
# 加载鸢尾花数据集
iris_data <- iris
# 设置随机种子以保证结果可复现
set.seed(123)
# 在每一数据列生成随机缺失值，每列数据随机缺失约5%
iris_data_missing <- iris_data %>%
  mutate_at(vars(-Species),~ifelse(runif(n()) < 0.05, NA, .))
# 查看缺失值数据
View(iris_data_missing)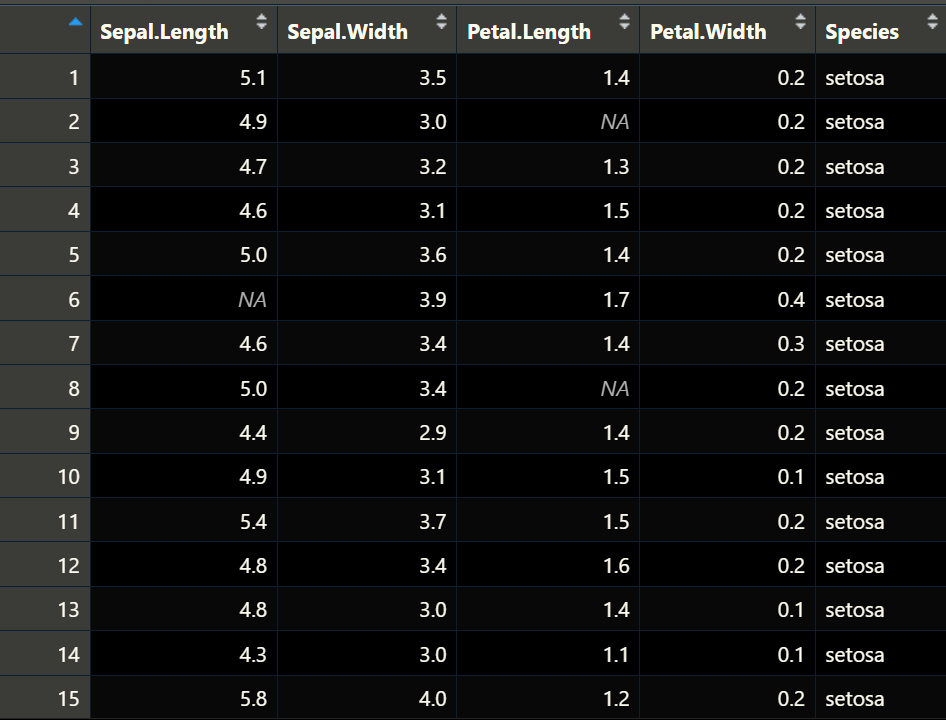

# 查看缺失值个数
iris_data_missing %>% is.na() %>% table()

1. 删除缺失值所在观测行

该方法简单粗暴，但==仅适用于大数据集中缺失值较少的情况==，此处仅演示如何操作：

# 删除包含缺失值的行
iris_data_clean <- na.omit(iris_data_missing)

2. 均值/中位数/众数插补

1. 均值插补：

   • 适用情况： 当数据呈正态分布或近似正态分布时，均值插补是一种合适的选择。均值对异常值敏感，因此如果存在大量异常值，均值可能不是最佳选择。

   • 优点： 简单易实现，不改变数据的总体均值。

   • 缺点： 对异常值敏感，可能引入偏差。

2. 中位数插补：

   • 适用情况： 当数据存在偏态分布或包含异常值时，中位数插补更为稳健。它对数据的中心位置具有鲁棒性，不受极端值的影响。
   • 优点： 对异常值不敏感，适用于偏态数据。
   • 缺点： 相较于均值，中位数插补可能会引入更多的不确定性。

3. 众数插补：

   • 适用情况： 对于分类变量或具有明显模态分布的数据，众数插补是一种合适的选择。它适用于离散型数据或在特定取值上有高峰值的情况。
   • 优点： 适用于离散型数据，不改变数据的整体分布。
   • 缺点： 在连续型数据中使用众数可能会失去一些信息，尤其是当数据分布较为均匀时。

   ==此处不对数据分布进行检验==，仅分别演示如何操作：

   # 1. 
   # 在每个类别（Species）的每一列进行均值插补
   iris_data_imputed <- iris_data_missing %>%
     group_by(Species) %>%
     mutate_at(vars(-Species), ~ifelse(is.na(.), mean(., na.rm = TRUE), .))
   
   # 2. 
   # 在每个类别（Species）的每一列进行中位数插补
   iris_data_imputed <- iris_data_missing %>%
     group_by(Species) %>%
     mutate_at(vars(-Species), ~ifelse(is.na(.), median(., na.rm = TRUE), .))
   
   # 3. 
   # 定义函数，用于获取每列的众数
   get_mode <- function(x) {
     unique_x <- unique(x)
     unique_x[which.max(tabulate(match(x, unique_x)))]
   }
   # 在每个类别（Species）的每一列进行众数插补
   iris_data_imputed <- iris_data_missing %>%
     group_by(Species) %>%
     mutate_at(vars(-Species), ~ifelse(is.na(.), get_mode(.), .))

3. 线性回归插补

当某些变量之间存在相关关系时，可以使用该插补方法，即用解释变量预测响应变量的缺失值。下面根据Sepal.Length预测Sepal.Width。当解释变量和响应变量均存在缺失值时，应先用其他方法插补解释变量，再进行回归预测。此处参考公众号医学和生信笔记中有关simputation包的使用^[1]^，有关该包的更多使用方法参见参考资料链接。

# 1. 下载并载入simputation包
# install.packages('simputation', dependencies = T)
# library(simputation)

# 2. 使用simputation包自带函数进行Sepal.Length列的中位数插补
iris_Length_imputed <- iris_data_missing %>% 
  impute_median(Sepal.Length ~ Species) # 根据Species这一列分组分别进行中位数插补

# 3. 使用线性回归方法插补Sepal.Width列
iris_Width_imputed  <- iris_Length_imputed %>% 
  impute_lm( Sepal.Width ~ Sepal.Length)

4. 多重插补

当缺失值模式复杂时，多重插补可以为一个缺失值生成多个估计值从而生成多个完整的数据集并进行综合分析，这样可以反映缺失数据真实值的不确定性。mice（Multiple Imputation by Chained Equations）是一个用于多重插补的R包，插补方法是通过使用“链式方程”（chained equations）进行的，也被称为多变量插补（Multivariate Imputation by Chained Equations，MICE）。本部分参考公众号庄闪闪的R语言手册中有关mice包的使用^[2]^，仅涉及缺失值填补方法部分，有关该包的更多使用方法参见参考资料链接。

library(mice)
# 以Species列分组进行多重插补，插补次数m=5次，迭代次数maxit=50次，数值型数据方法指定'pmm'
tmp <- iris_data_missing %>%
  mice(m=5,maxit=50,meth='pmm',seed=500,group="Species")
summary(tmp)

# 使用complete()函数返回完整的数据集，action的参数值表示选择第几次的插补值来填补原始数据集
finalData <- complete(tmp,action = 5)

# 通过图像比较选择合适插补值
# 蓝色线代表原始数据，红色线代表每一次插补得到的数据
# 在左边图形（该图形包含了全部插值结果）中确定拟合度最好的线，然后通过修改imp的值，直到在右侧图形中找到那条线。
densityplot(tempData,~ Ozone | .imp == c(1,2))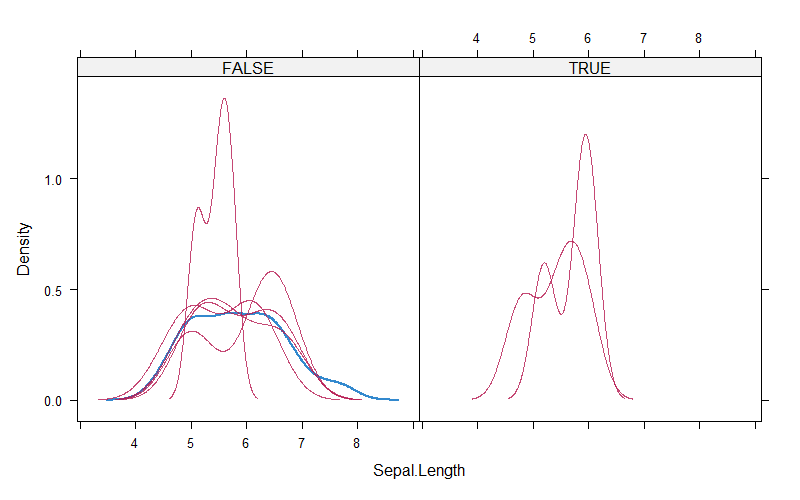

参考资料：

[1] R语言缺失值插补之simputation包，医学和生信笔记：https://mp.weixin.qq.com/s/pJt5F6Ydj0eeV1S6CXiWaw

[2] 超详细的 R 语言插补缺失值教程来啦~，庄闪闪的R语言手册：https://mp.weixin.qq.com/s/DelYXpjmfgmA600H0b5wIA

本文由博客一文多发平台 OpenWrite 发布！