一、Jenkins 介绍
Jenkins是由java编写的一款开源软件。作为一款非常流行的CI(持续集成)工具,用于构建和测试各种项目,以及监视重复工作的执行,例如软件工程的构建或在 cron 下设置的 jobs。
Jenkins的主要目的是持续、自动的软件版本构建、测试项目;监控软件开放流程,快速问题定位及处理,提高开发效率。
Jenkins 特点:
- 开源的java语言开发持续集成工具,支持持续集成,持续部署。
- 易于安装部署配置:可通过yum安装,或下载war包以及通过docker容器等快速实现安装部署,可方便web界面配置管理。
- 消息通知及测试报告:集成RSS/E-mail通过RSS发布构建结果或当构建完成时通过e-mail通知,生成JUnit/TestNG测试报告。
- 分布式构建:支持Jenkins能够让多台计算机一起构建/测试。
- 文件识别:Jenkins能够跟踪哪次构建生成哪些jar,哪次构建使用哪个版本的jar等。
- 丰富的插件支持:支持扩展插件,你可以开发适合自己团队使用的工具,如git,svn,maven,docker等。
二、Jenkins 安装和持续集成环境配置
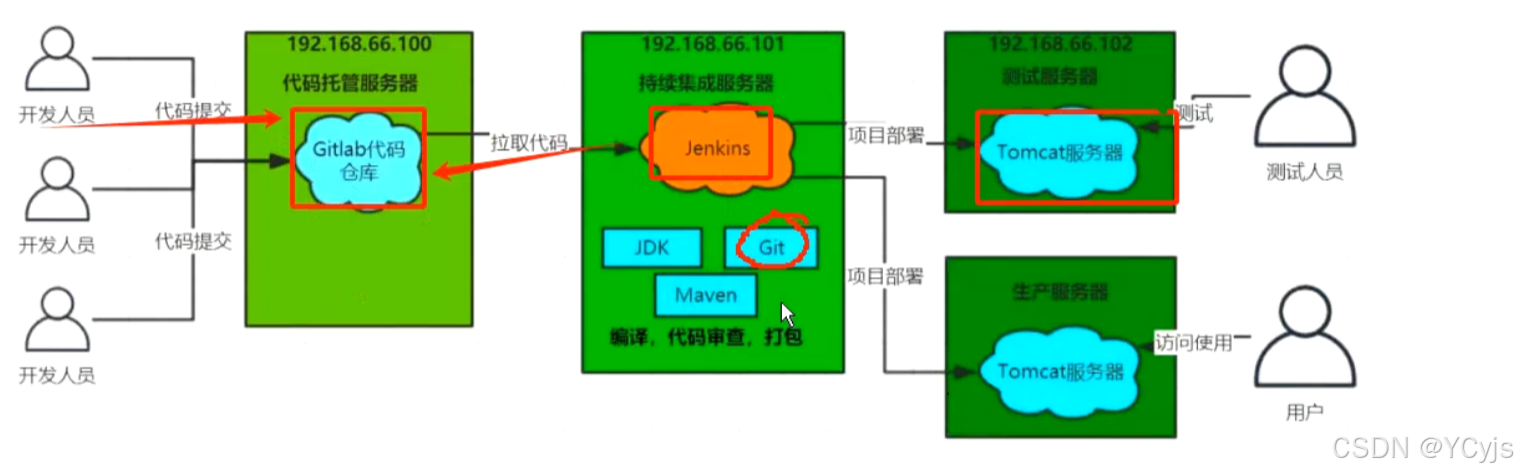
2.1、配置
| 服务器类型 | IP地址 | 软件/工具 | 版本/描述 |
|---|---|---|---|
| 代码托管服务器 | 192.168.88.10 | Gitlab | 用于代码的版本控制和托管 |
| 持续集成服务器 | 192.168.88.20 | Jenkins,JDK17,Maven3,Git | 持续集成工具,用于自动化构建和测试 |
| 应用测试服务器 | 192.168.88.30 | JDK1.8,Tomcat8.5 |
1、所有机器
setenforce 0
systemctl disable --now firewalld
2.2、Gitlab安装
①、安装相关依赖
yum -y install policycoreutils openssh-server openssh-clients postfix git
systemctl enable --now sshd
systemctl enable --now postfix
②、上传 gitlab-ce-12.3.0-ce.0.el7.x86_64.rpm 文件到 /opt 目录
cd /opt
rpm -ivh gitlab-ce-12.3.0-ce.0.el7.x86_64.rpm
修改 gitlab 访问地址和端口配置
vim /etc/gitlab/gitlab.rb
external_url 'http://192.168.88.10:82'
nginx['listen_port'] = 82重载配置及启动 gitlab
gitlab-ctl reconfigure
gitlab-ctl restart
浏览器访问:http://192.168.88.10:82 ,如果显示 502,稍等片刻再刷新
1、设置管理员 root 用户的新密码,注意有格式要求,这里设置成 root@123
2、使用管理员 root 用户登录(root/root@123)
3、登录后点击页面右上方的用户选项下拉选择【Settings】,点击左边菜单【Preferences】,在【Localization】的【Language】中选择【简体中文】,点击【Save changes】按钮,再刷新页面使用中文显示。
2.2.1、补充
浏览器访问:http://192.168.88.10:82 ,如果显示 502,稍等片刻再刷新
1、设置管理员 root 用户的新密码,注意有格式要求,这里设置成 root@123
2、使用管理员 root 用户登录(root/root@123)
3、登录后点击页面右上方的用户选项下拉选择【Settings】,点击左边菜单【Preferences】,在【Localization】的【Language】中选择【简体中文】,点击【Save changes】按钮,再刷新页面使用中文显示。
4、Gitlab添加组、创建用户、创建项目
①、创建群组
点击页面左上方的【GitLab】图标,点击 【新建群组】
【群组名称】、【群组URL】、【群组描述】都设置成 devops_group
【可见性级别】设置成 私有
其他都保持默认值,点击 【创建群组】
②、创建项目
点击 【新建项目】
【项目URL】群组选项下拉选择 devops_group
【项目名称】设置成 web_demo
【项目描述】设置成 web_demo
【可见等级】设置成 私有
点击 【创建项目】
③、创建用户
点击页面上方的【扳手】图标进入“管理区域”
点击 【新建用户】
【姓名】设置成 zhangsan
【用户名】设置成 zhangsan
【电子邮箱】设置成 zhangsan@pp.com
这里密码暂不设置,其他都保持默认值,先点击 【创建用户】
注:Access level:
Regular(表示的是普通用户,只能访问属于他的组和项目);
Admin(表示的是管理员,可以访问所有组和项目)
创建好用户后再点击右上角的【Edit】,可在这里设置密码,如 zhangsan@123
④、将用户添加到组中
点击页面上方的【群组】下拉选择 devops_group
点击左边菜单【成员】
【添加成员到 devops_group】选择 zhangsan,角色权限选择 Owner
点击 【添加到群组】
注:角色权限:
Guest:可以创建issue、发表评论,不能读写版本库
Reporter:可以克隆代码,不能提交,QA、PM可以赋予这个权限
Developer:可以克隆代码、开发、提交、push,普通开发可以赋予这个权限
Maintainer:可以创建项目、添加tag、保护分支、添加项目成员、编辑项目,核心开发可以赋予这个权限
Owner:可以设置项目访问权限(Visibility Level)、删除项目、迁移项目、管理组成员,开发组组长可以赋予这个权限
使用自己创建的账户进行管理
退出当前账户,使用自己创建的账户 zhangsan 登录(zhangsan/zhangsan@123)
第一次登录会被强制要求修改密码(zhangsan/zhangsan@123),可与旧密码相同,再重新登录
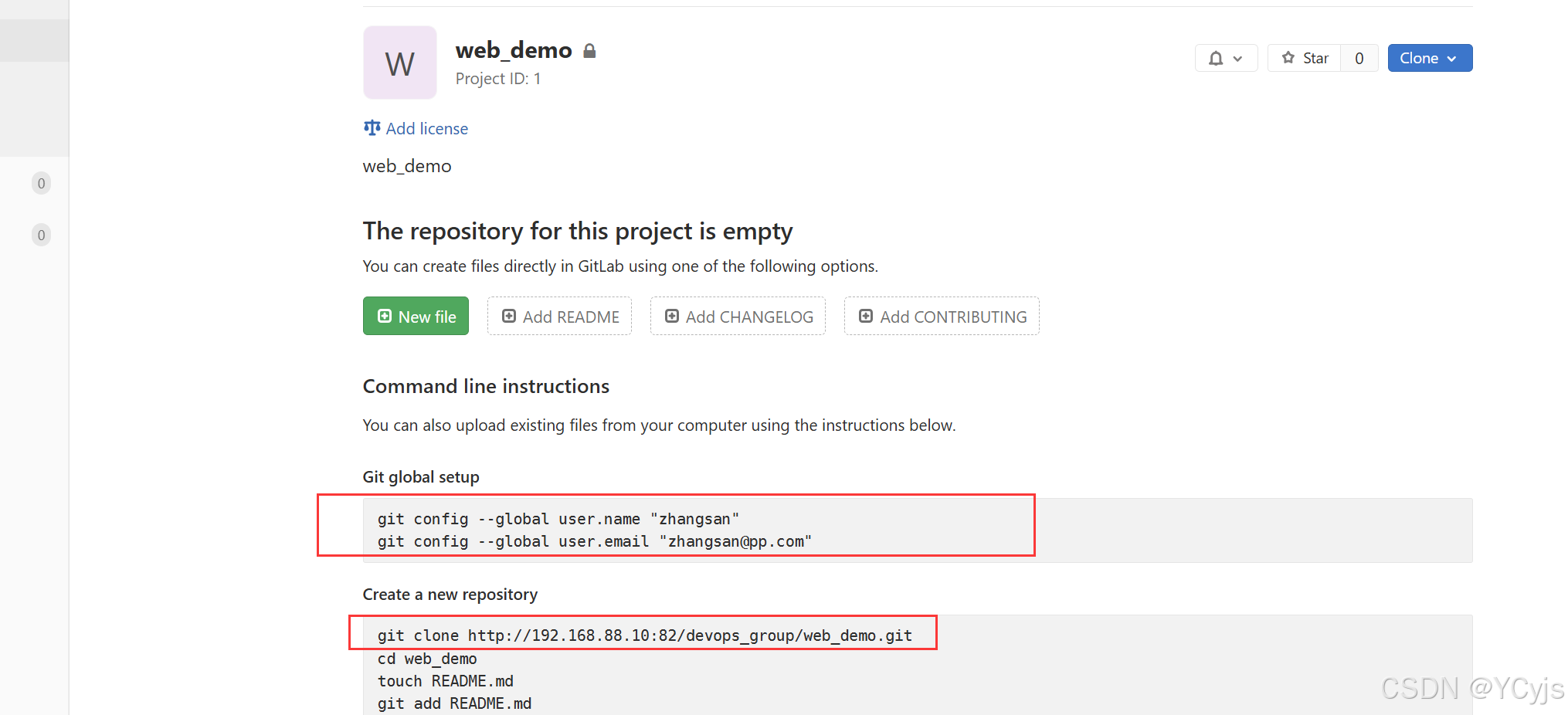
源码上传到Gitlab仓库
git config --global user.name "zhangsan"
git config --global user.email "zhangsan@pp.com"
cd ~
git clone http://192.168.80.10:82/devops_group/web_demo.git
账号/密码:zhangsan/zhangsan@123
ls -A web_demo/
上传 web_demo.zip 文件到 /opt 目录
cd /opt
unzip web_demo.zip
mv web_demo/* /root/web_demo/
cd /root/web_demo
git add .
git commit -m "init web_demo"
git push -u origin master
账号/密码:zhangsan/zhangsan@123
点击页面上方的【项目】下拉选择 web_demo,即可看到上传的代码
三、Jenkins安装
jenkins建议安装LTS长期支持版本,而不是安装每周更新版本,jenkins安装指定版本(https://mirrors.jenkins-ci.org/redhat/)
jenkins 清华大学开源软件镜像站
https://mirrors.tuna.tsinghua.edu.cn/jenkins/redhat/
JDK下载版本
https://adoptium.net/zh-CN/temurin/releases/?version=17&arch=x64&os=linux&package=jdk
根据版本而定 jdk
1、安装JDK17配置
放入文件到opt下jdk和jenkins
tar zxvf OpenJDK17U-jdk_x64_linux_hotspot_17.0.13_11.tar.gz -C /usr/local/
cd /usr/local/
mv jdk-17.0.13+11/ jdk-17.0.13
2、环境变量
vim /etc/profile
最后行尾
export JAVA_HOME=/usr/local/jdk-17.0.13
export JRE_HOME=$JAVA_HOME/jre
export CLASSPATH=.:${JAVA_HOME}/lib:${JRE_HOME}/lib
export PATH=$JAVA_HOME/bin:$JRE_HOME/bin:$PATHsource /etc/profile
java -version
3、安装jenkins
wget -O /etc/yum.repos.d/jenkins.repo https://pkg.jenkins.io/redhat-stable/jenkins.repo --no-check-certificate
rpm --import https://pkg.jenkins.io/redhat-stable/jenkins.io.key
yum install epel-release -y
yum install jenkins -y jenkins-2.479-1.1.noarch.rpm
如果公钥不成功
sudo yum -y install jenkins --nogpgcheck
补充
不行就改repo
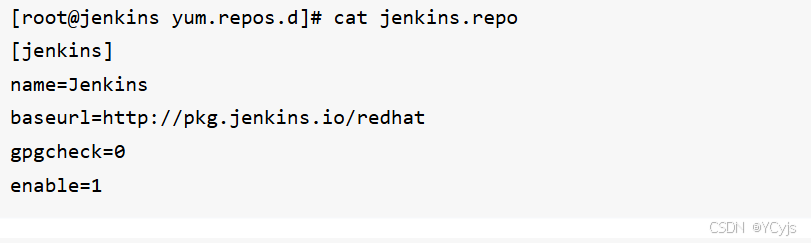
4、查看
rpm -qa jenkins
rpm -ql jenkins
5、新版本的 jenkins 还要在 /usr/lib/systemd/system/jenkins.service 文件中修改用户名和端口
vim /usr/lib/systemd/system/jenkins.service
User=root
Group=root
Environment="JAVA_HOME=/usr/local/jdk-17.0.13/"
Environment="JENKINS_PORT=8888"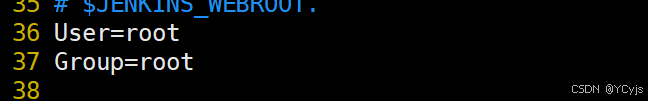

![]()
6、给权限
chown -R jenkins:jenkins /var/lib/jenkins
chown -R jenkins:jenkins /var/cache/jenkins
7、启动
systemctl daemon-reload
systemctl start jenkins
systemctl enable jenkins
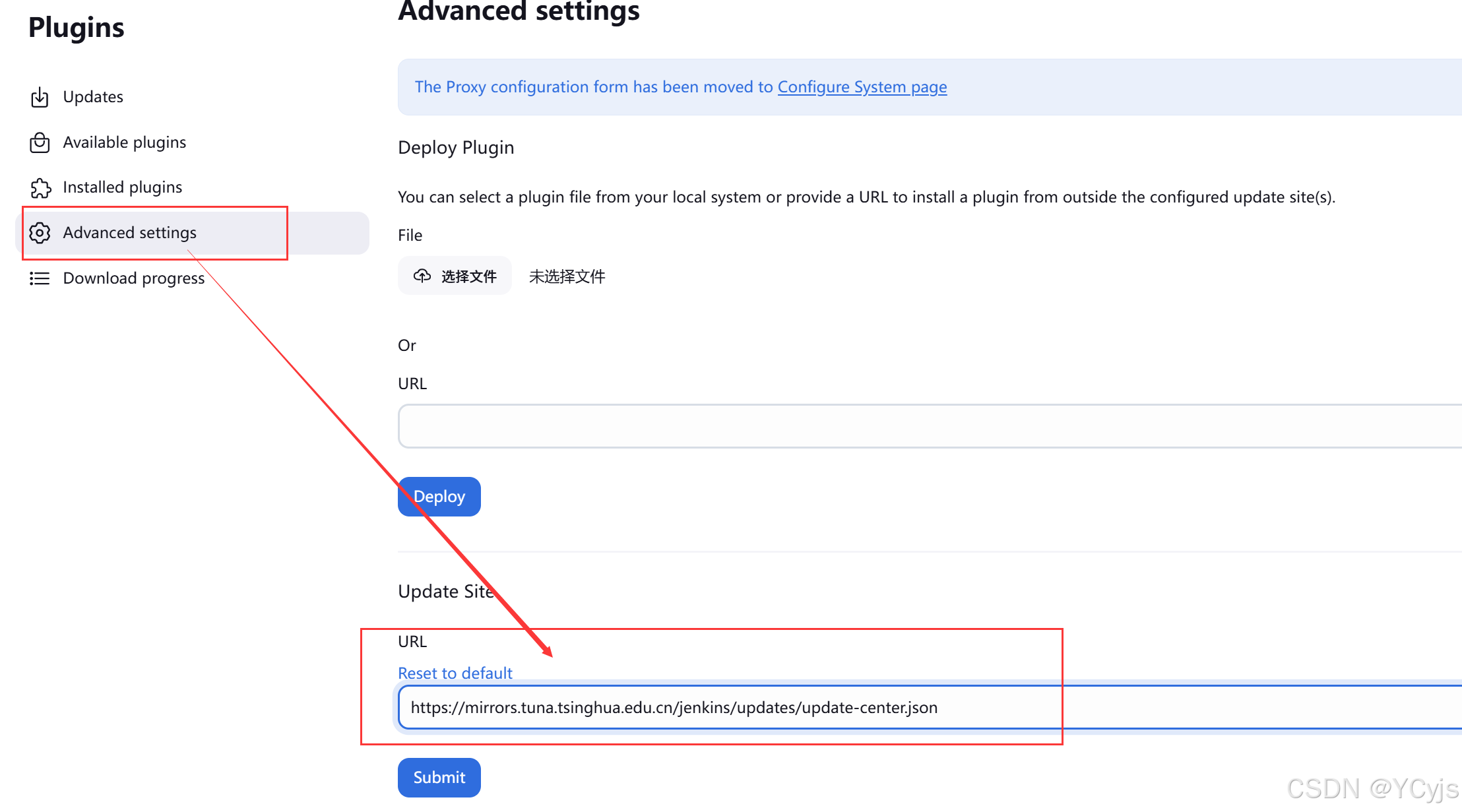
8、修改源地址
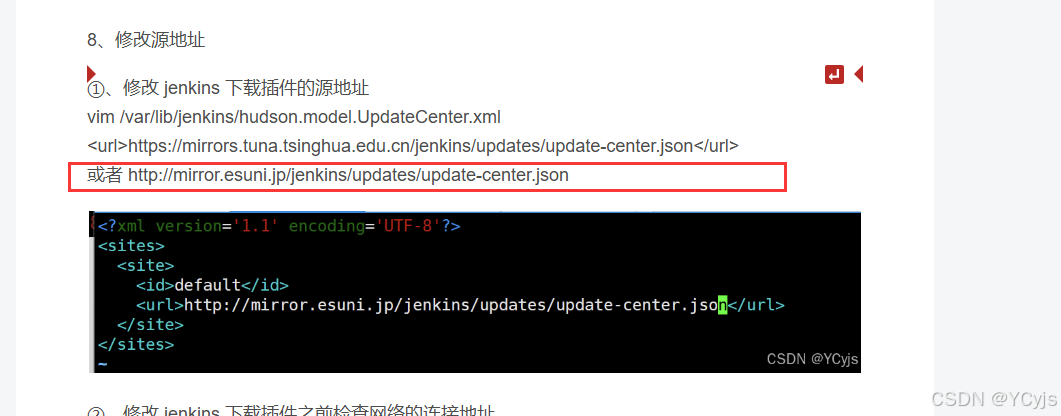
①、修改 jenkins 下载插件的源地址
vim /var/lib/jenkins/hudson.model.UpdateCenter.xml
<url>https://mirrors.tuna.tsinghua.edu.cn/jenkins/updates/update-center.json</url>
或者 http://mirror.esuni.jp/jenkins/updates/update-center.json
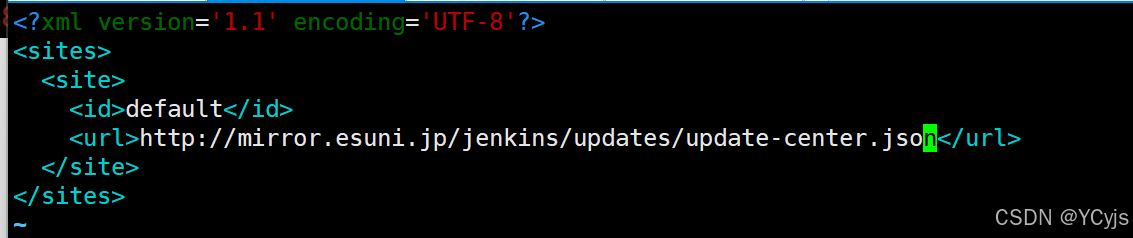
②、修改 jenkins 下载插件之前检查网络的连接地址
vim /var/lib/jenkins/updates/default.json
goole
改成
"connectionCheckUrl":"https://www.baidu.com/"

sed -i 's#https://www.google.com#https://www.baidu.com#' /var/lib/jenkins/updates/default.json
systemctl restart jenkins
netstat -lnutp | grep 8888
浏览器访问:http://192.168.88.20:8888
获取并输入 admin 账户密码
cat /var/lib/jenkins/secrets/initialAdminPassword
9、安装插件
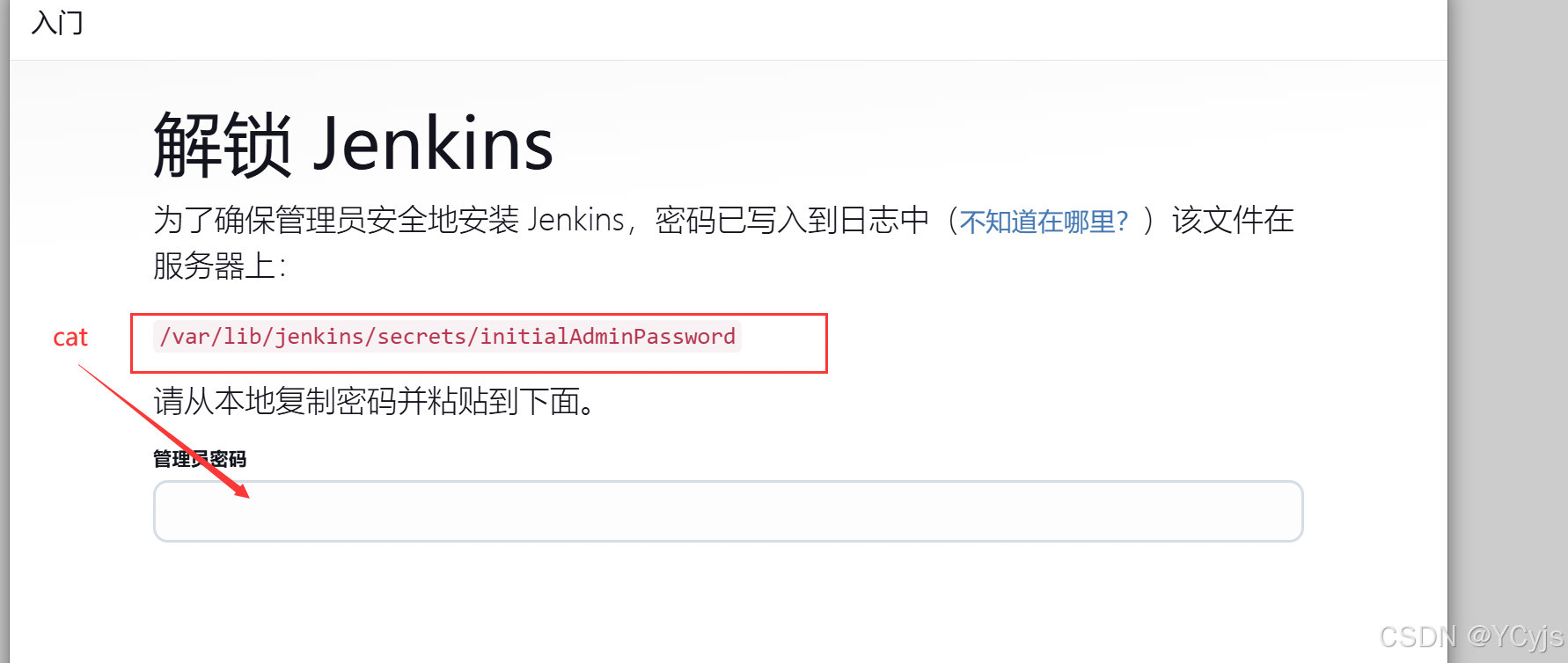
先不安装
创建第一个管理员用户,如 zhangsan/zhangsan@123
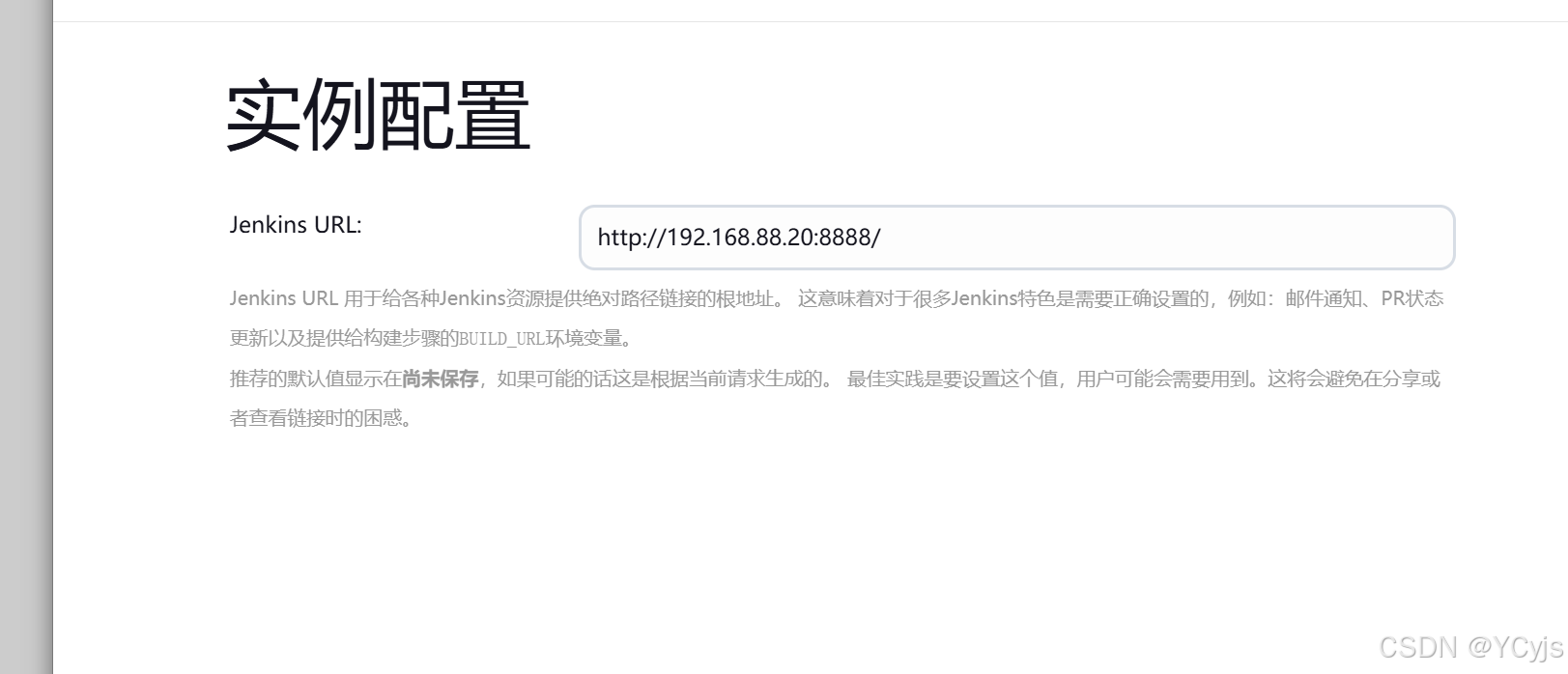
Jenkins URL 保持默认即可
下载插件
修改地址(我们之前在8的时候改过了,如果没有修改也可以修改)
https://mirrors.tuna.tsinghua.edu.cn/jenkins/updates/update-center.json
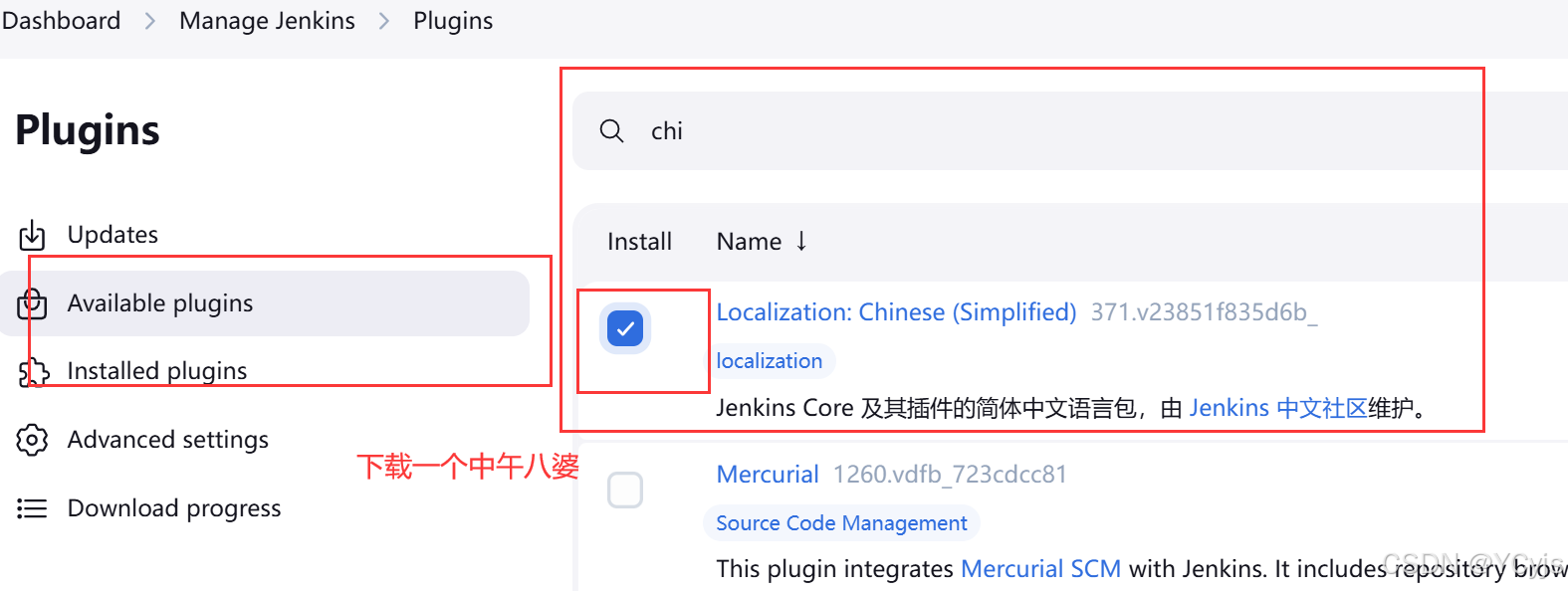
下载一个中文包

或者网页上
http://192.168.88.20:8888/http://192.168.88.20:8888/restart
3.1、Jenkins 用户权限管理
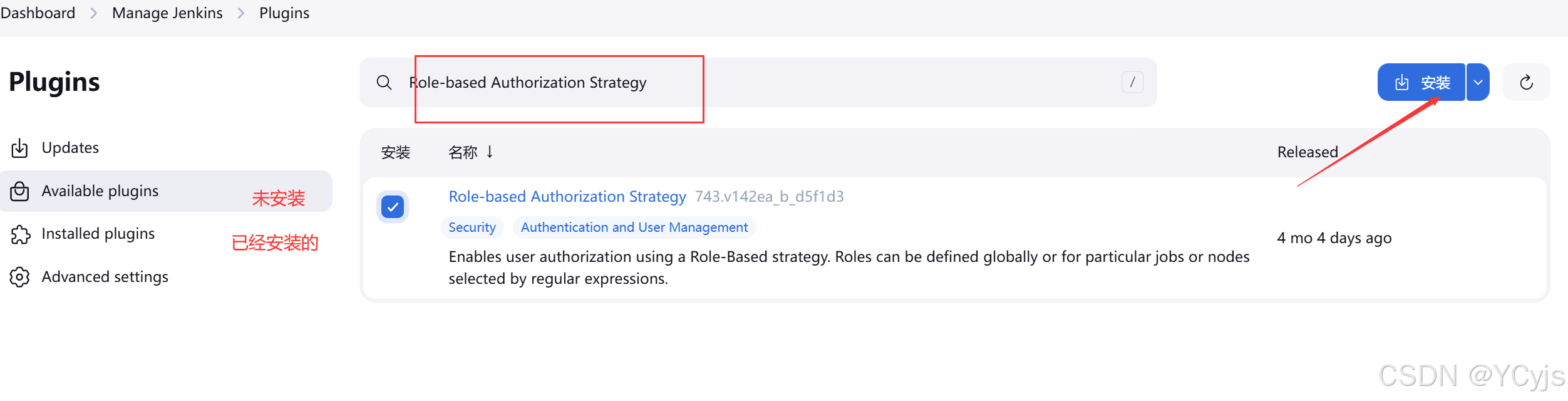
1、安装用户管理插件
Manage Jenkins -> 管理插件-可选插件 -> 搜索 Role-based Authorization Strategy 插件选中直接安装即可。
基于角色的授权策略
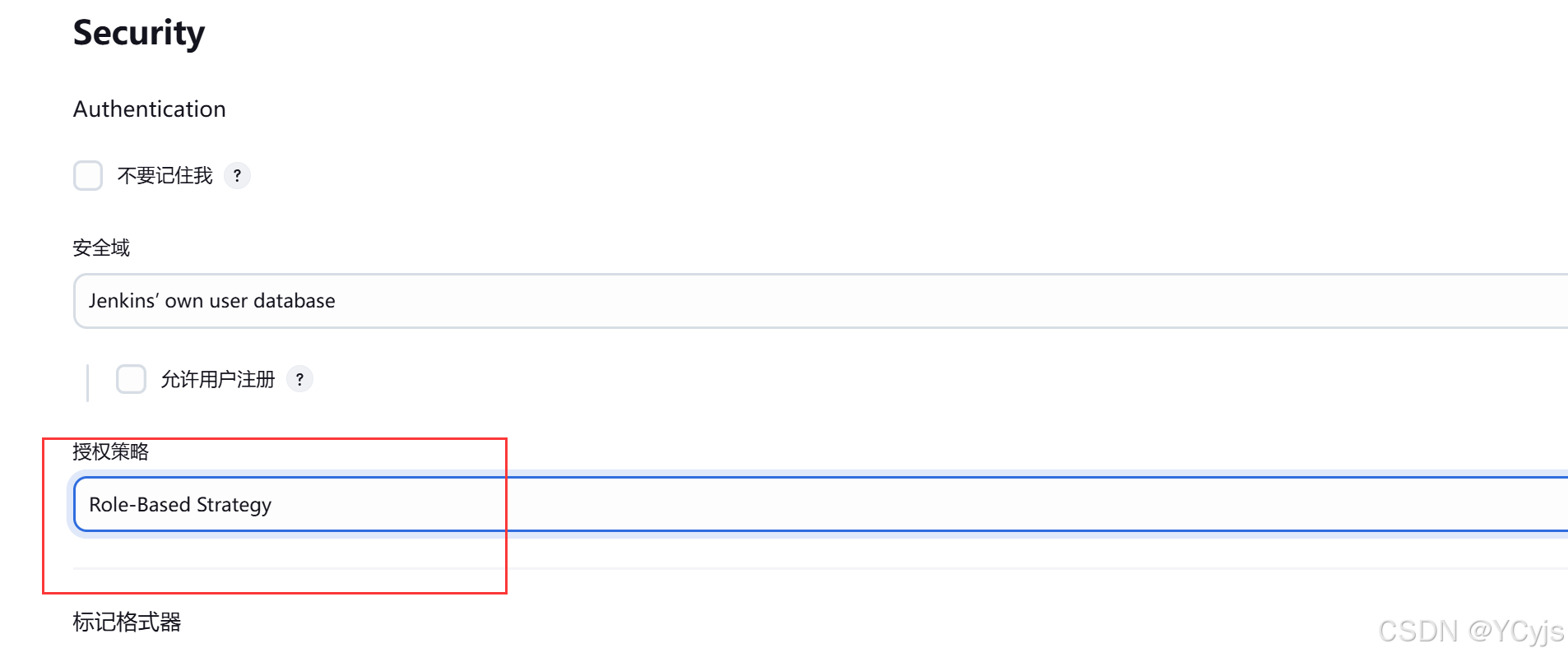
2、开启权限全局安全配置
Manage Jenkins -> 全局安全设置-授权策略 -> 选中 Role-Based Strategy -> 应用-->保存
策略换成我们刚刚下载的基于角色的授权策略
3、创建角色
Manage Jenkins -> Manage and Assign Roles -> 选中 Manage Roles
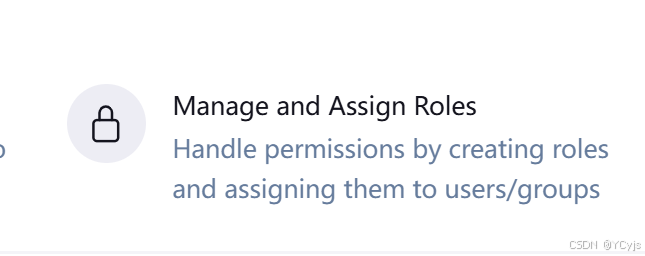

Global roles(全局角色):管理员等高级用户可以创建基于全局的角色
默认是有一个admin用户的,是所有权限都有的,所有权限都是勾选了的。
添加一个角色 user,这个角色需要绑定Overall下面的Read权限,是为了给所有用户绑定最基本的Jenkins访问权限。

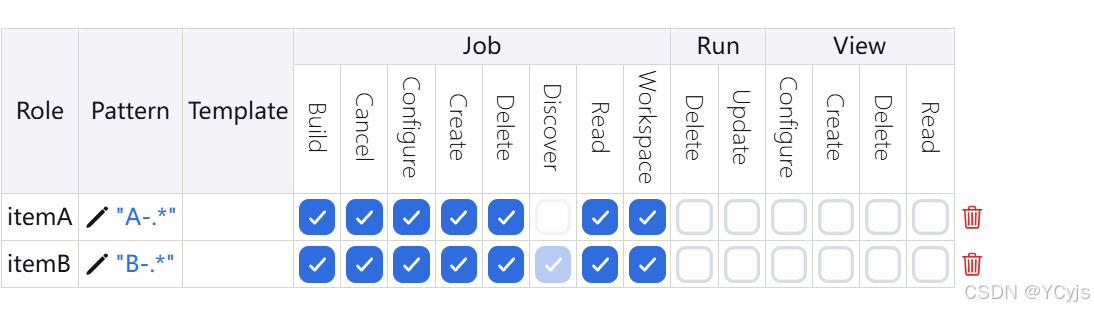
Item roles(项目角色):针对某个或者某些项目的角色
Role to add:表示添加的项目角色
Pattern:是用来做正则匹配的(匹配的内容是Job的项目名),根据正则匹配到的项目,项目角色就都有权限
新建一个 ItemA 项目角色,使用正则表达式绑定“A-.*”,意思是只能操作 A- 开头的项目,项目角色添加上所有的Job权限。
新建一个 ItemB 项目角色,使用正则表达式绑定“B-.*”,意思是只能操作 B- 开头的项目,项目角色添加上所有的Job权限。
应用---保存
4、创建节点角色
Node roles(节点角色):节点相关的权限
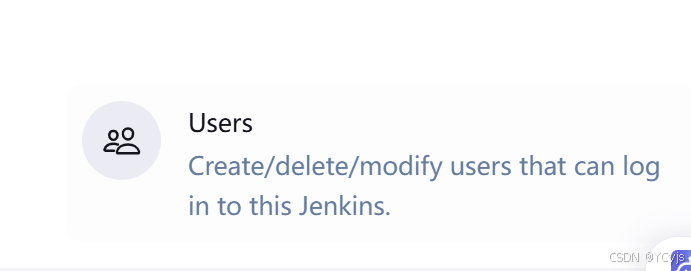
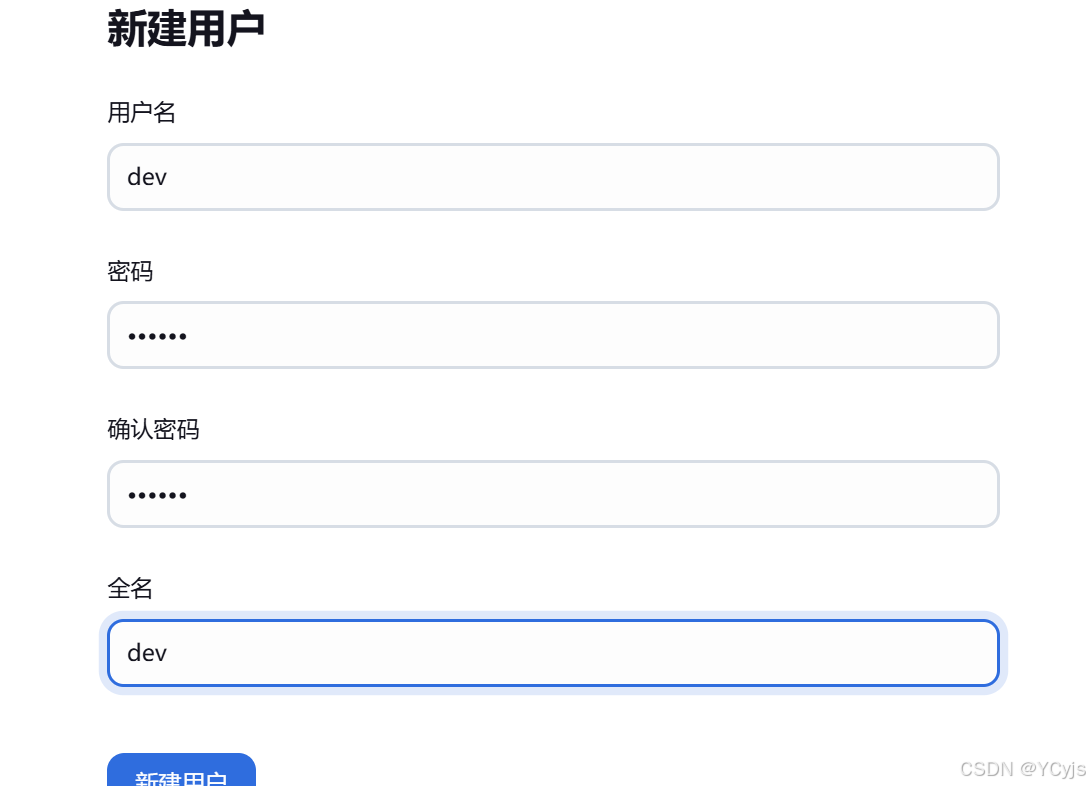
给用户分配角色
Manage Jenkins -> Manage Users -> 新建用户 -> 创建两个用户:dev 和 ops
开发和运维
重新登录新创建的用户 dev,此时会显示已经没有任何权限。
项目绑定的是
重新登录管理员账户操作
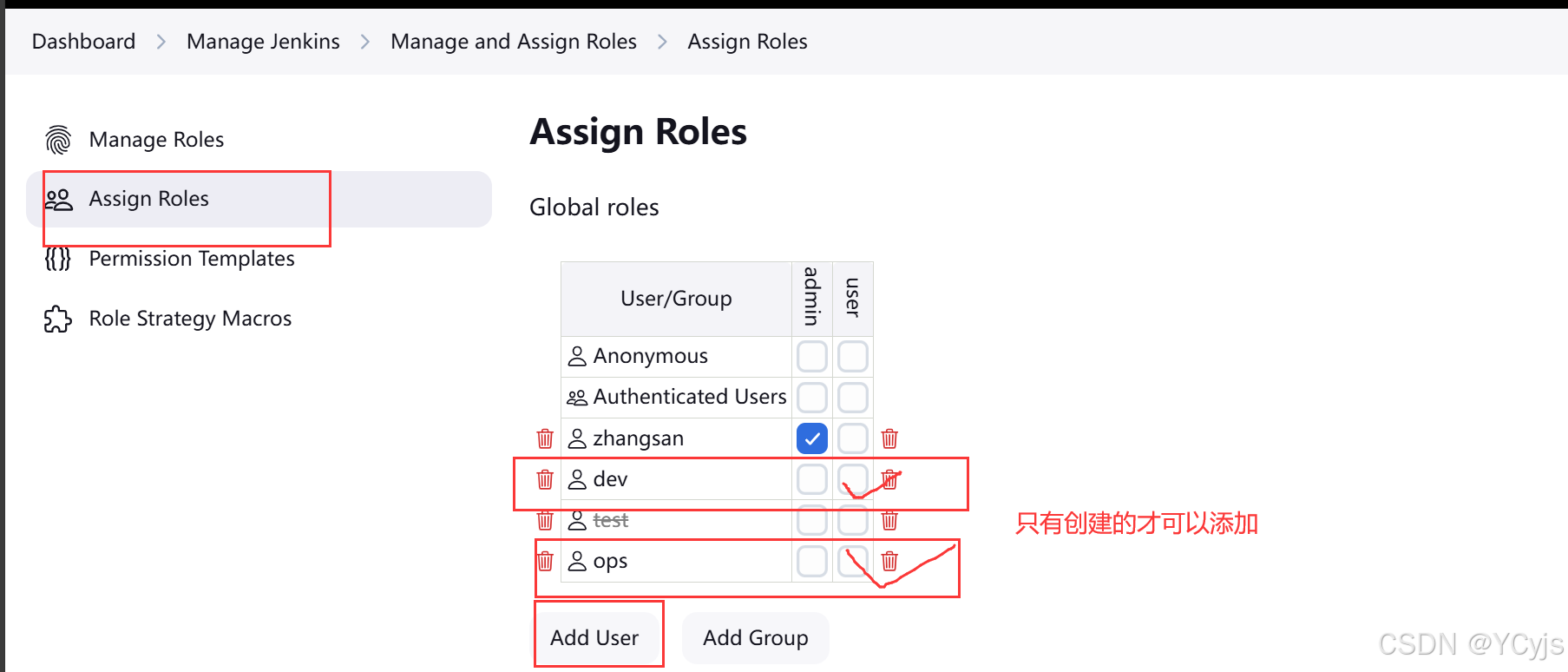
Manage Jenkins -> Manage and Assign Roles -> 点击 Assign Roles
dev 用户分别绑定 user 和 ItemA 角色
ops 用户分别绑定 user 和 ItemB 角色
应用-保存
5、创建项目测试权限
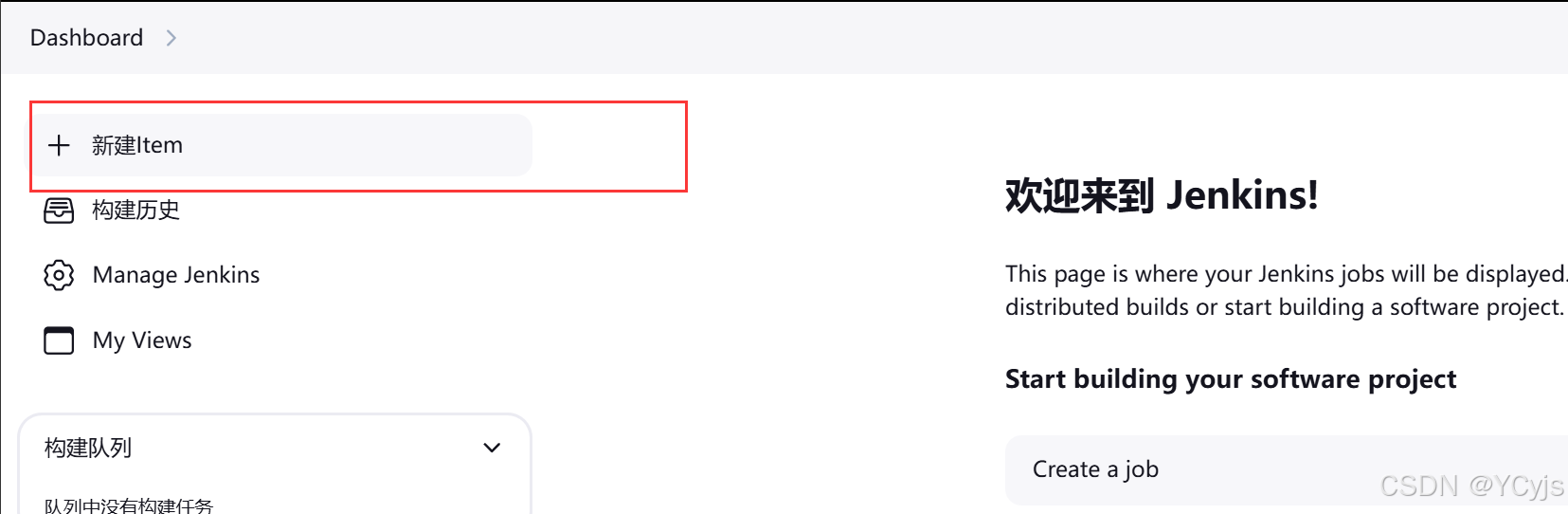
新建Item -> 创建两个项目,分别为 A-web1 和 B-web1
简单创建,就确定就行
测试
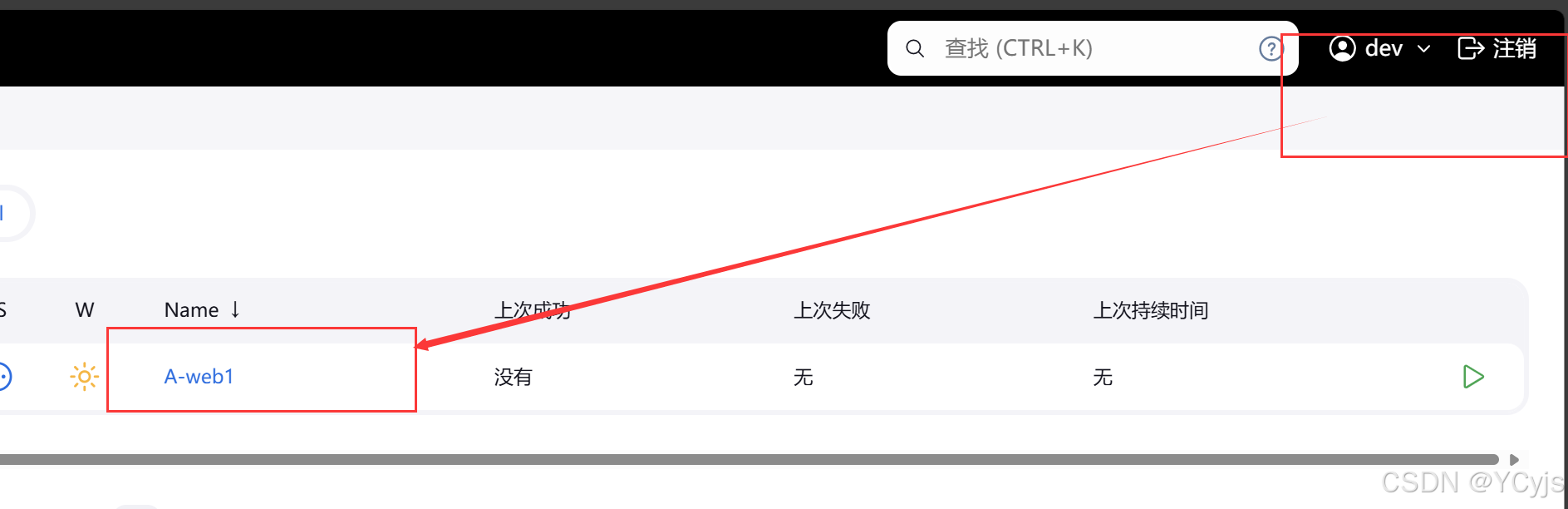
结果为:
dev 用户登录,只能看到 A-web1 项目
ops 用户登录,只能看到 B-web1 项目
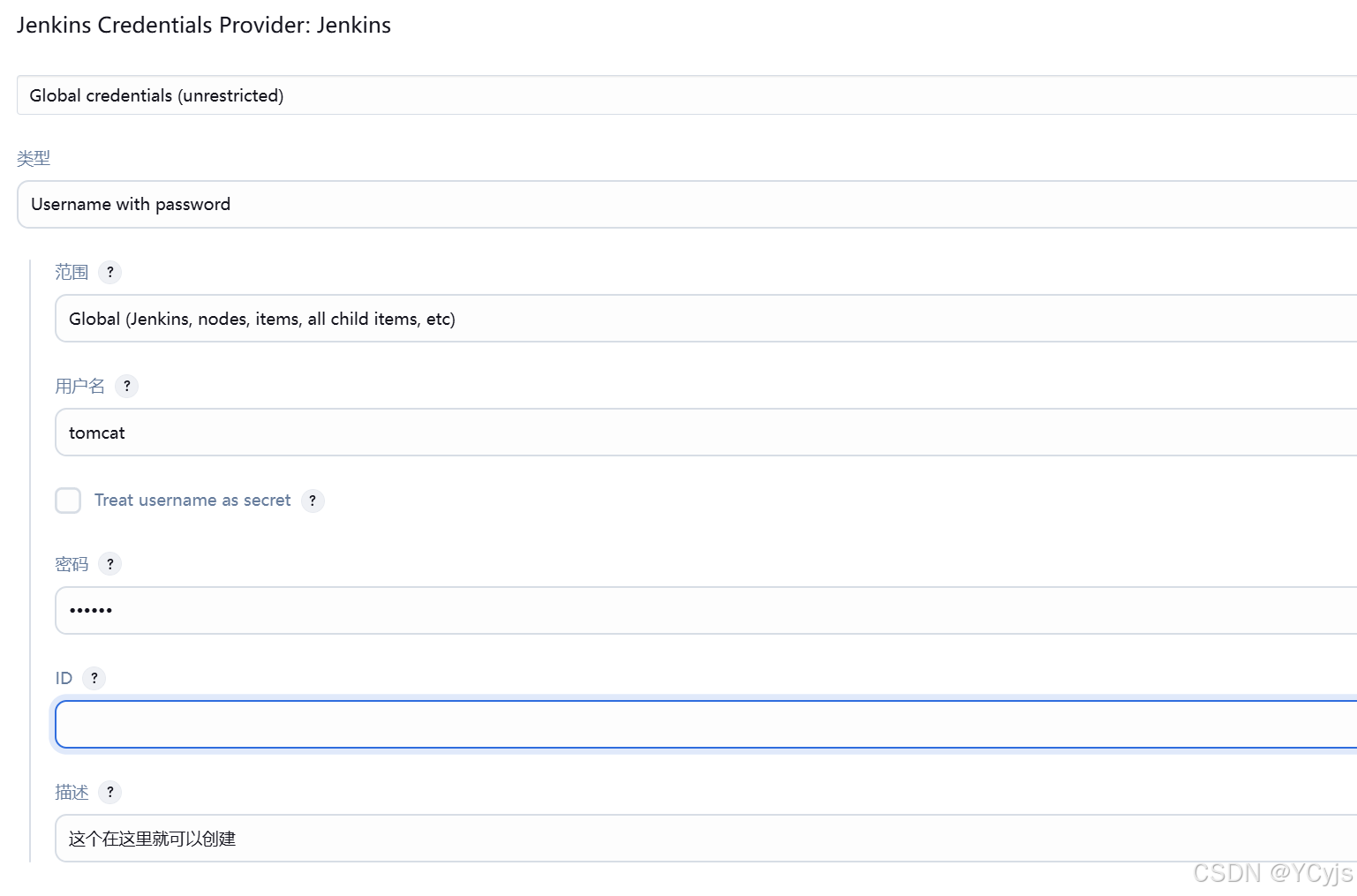
3.2、Jenkins 凭据管理
凭据可以用来存储需要密文保护的数据库密码、Gitlab密码信息、Docker私有仓库密码等,以便Jenkins可以和这些第三方的应用进行交互。要在Jenkins使用凭据管理功能,需要安装Credentials Binding插件(推荐的插件已默认安装)。
点击右上角用户名 -> 凭据 -> 点击 Jenkins 全局 -> 添加凭据 


常用的凭据类型:
Username with password:用户名和密码。
SSH Username with private key:使用 SSH 用户和密钥。
Secret file:需要保密的文本文件,使用时 Jenkins 会将文件复制到一个临时目录中,再将文件路径设置到一个变量中, 等构建结束后,所复制的 Secret file 就会被删除。
Secret text:需要保存的一个加密的文本串,如钉钉机器人或 Github 的 api token。
Certificate:通过上传证书文件的方式。
为了让 Jenkins 支持从 Gitlab 拉取源码,需要安装 Git 插件以及在 linux 系统上安装 Git 工具。(之前已安装好了)
普通用户密码凭据
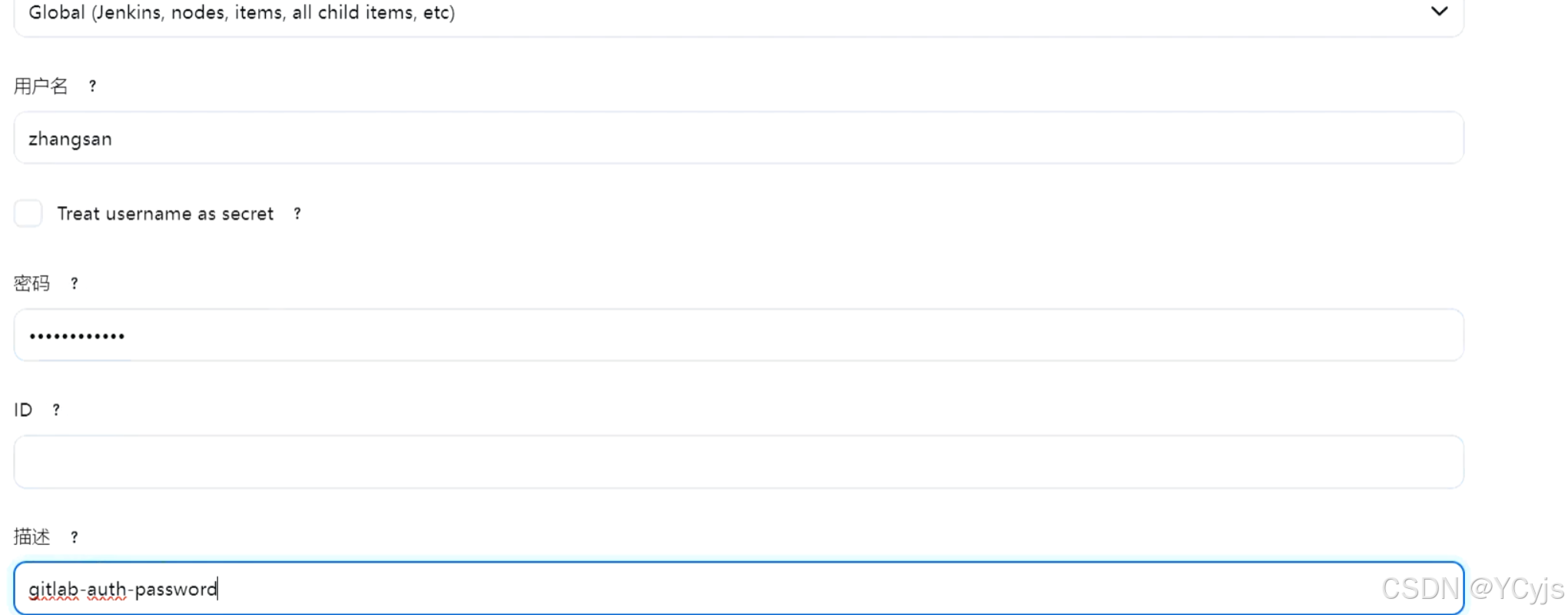
①、创建凭据
点击用户名下拉选择凭据 -> Jenkins 全局 -> 添加凭据
类型选择 "Username with password" ,输入 Gitlab 的用户名和密码(zhangsan/zhangsan@123),描述输入 gitlab-auth-password
点击 "确定"。

②、测试凭据是否可用
安装git插件
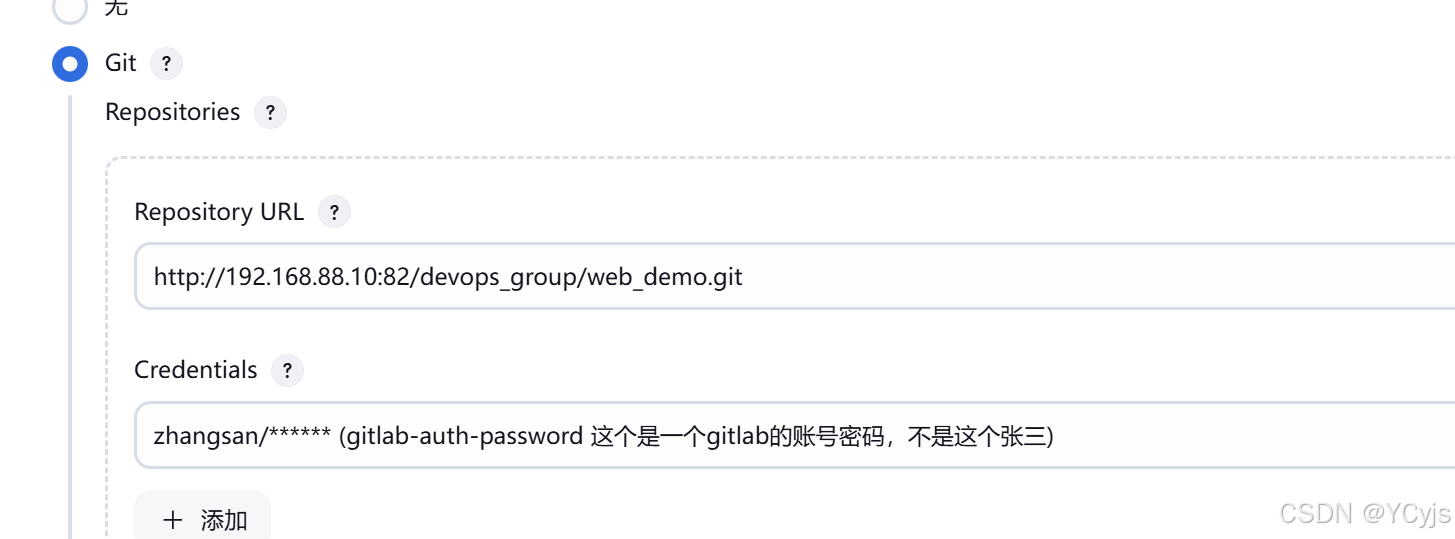
创建一个FreeStyle项目:新建Item -> 任务名称(test01) FreeStyle Project -> 确定
源码管理:选择 Git,Repository URL:http://192.168.88.10:82/devops_group/web_demo.git(可从 Gitlab 使用 HTTP 克隆),

Credentials 下拉选择 gitlab-auth-password,点击 保存。
③、构建
点击 Bulid Now 开始构建,查看控制台输出可以看到构建成功,构建后的包会生成在服务器的 /var/lib/jenkins/workspace/test-01 目录中。

3.3、SSH密钥类型
1、在 Jenkins 服务器上使用 root 用户生成免密的公钥和私钥
ssh-keygen -t rsa -P '' -f ~/.ssh/id_rsa
测试连接
ssh-copy-id root@192.168.88.10
- 这个命令用于将你的本地SSH公钥复制到远程计算机(在这个例子中是IP地址为192.168.88.10的计算机)
ssh root@192.168.88.10
这个命令用于通过SSH协议连接到远程计算机的root用户
(最好测试一下看看能不能到gitlab那台机器)
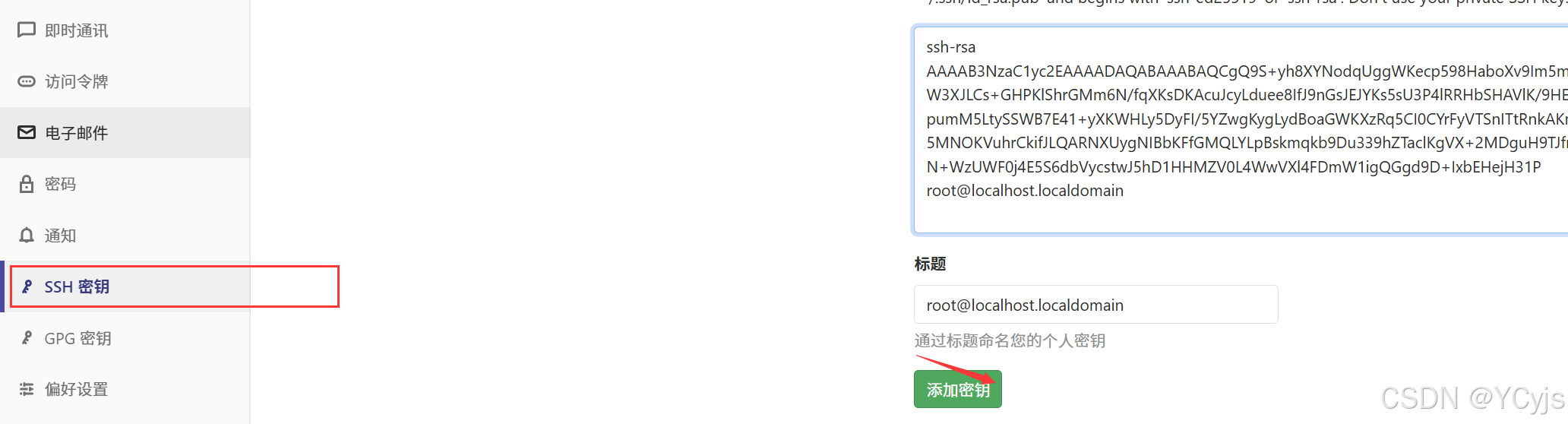
2、把生成的公钥放在 Gitlab 中
回到20机器
获取公钥内容
cat /root/.ssh/id_rsa.pub
以 root 账户登录Gitlab -> 点击头像下拉选择设置 -> SSH 密钥
复制刚才公钥文件的内容到这里,点击 添加密钥
3、在 Jenkins 中添加凭据,配置私钥
获取私钥内容
cat /root/.ssh/id_rsa
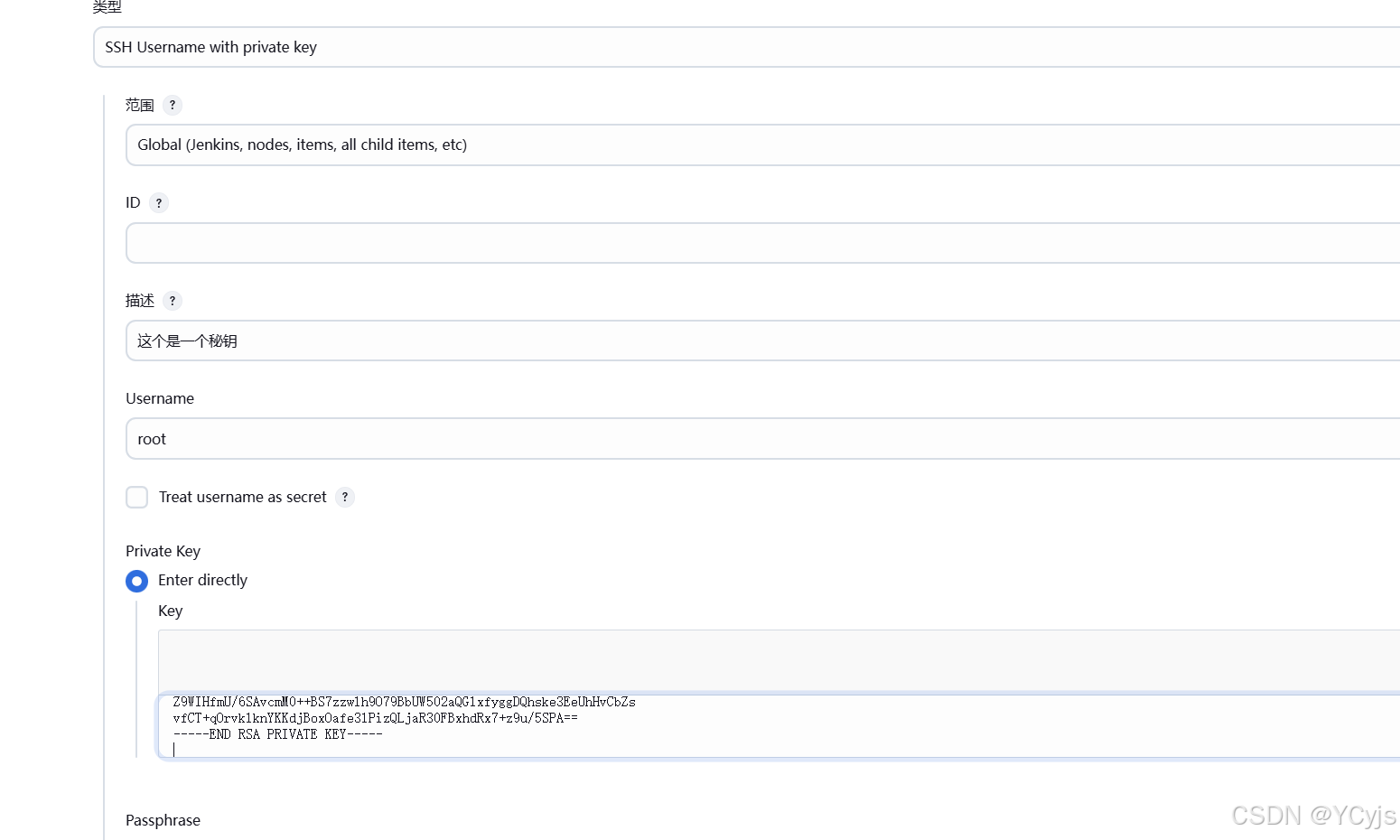
点击用户名下拉选择凭据 -> Jenkins 全局 -> 添加凭据
类型选择 "SSH Username with private key",描述输入 gitlab-auth-ssh,Username 输入生成私钥的用户名 root,
Private Key 下面选择 Enter directly,把刚才生成私钥文件内容复制过来
点击 "确定"。

点击全局
4、测试凭据是否可用
创建一个FreeStyle项目:新建Item-> 任务名称(test02) FreeStyle Project-> 确定
源码管理:选择 Git,Repository URL:git@192.168.88.10:devops_group/web_demo.git
(可从 Gitlab 使用 SSH 克隆),
Credentials 下拉选择 gitlab-auth-ssh,点击 保存。
尝试构建项目,如果代码可以正常拉取,代表凭据配置成功!
3.4、Jenkins 构建 Maven 项目
Maven 是一个主要用于 Java 项目的自动化构建工具。Maven 还可以用来构建和管理用 C#、Ruby、Scala 和其他语言开发的项目。
在 Jenkins 服务器上安装 Maven 来编译和打包项目
cd /opt
tar -zxvf apache-maven-3.6.2-bin.tar.gz
mv apache-maven-3.6.2 /usr/local/maven
vim /etc/profile
......
export MAVEN_HOME=/usr/local/maven
export PATH=$MAVEN_HOME/bin:${JAVA_HOME}/bin:$PATHsource /etc/profile
查看Maven版本
mvn -v
Jenkins 关联 JDK 和 Maven
tar xf jdk-8u171-linux-x64.tar.gz -C /usr/local/
Manage Jenkins -> Global Tool Configuration -> JDK
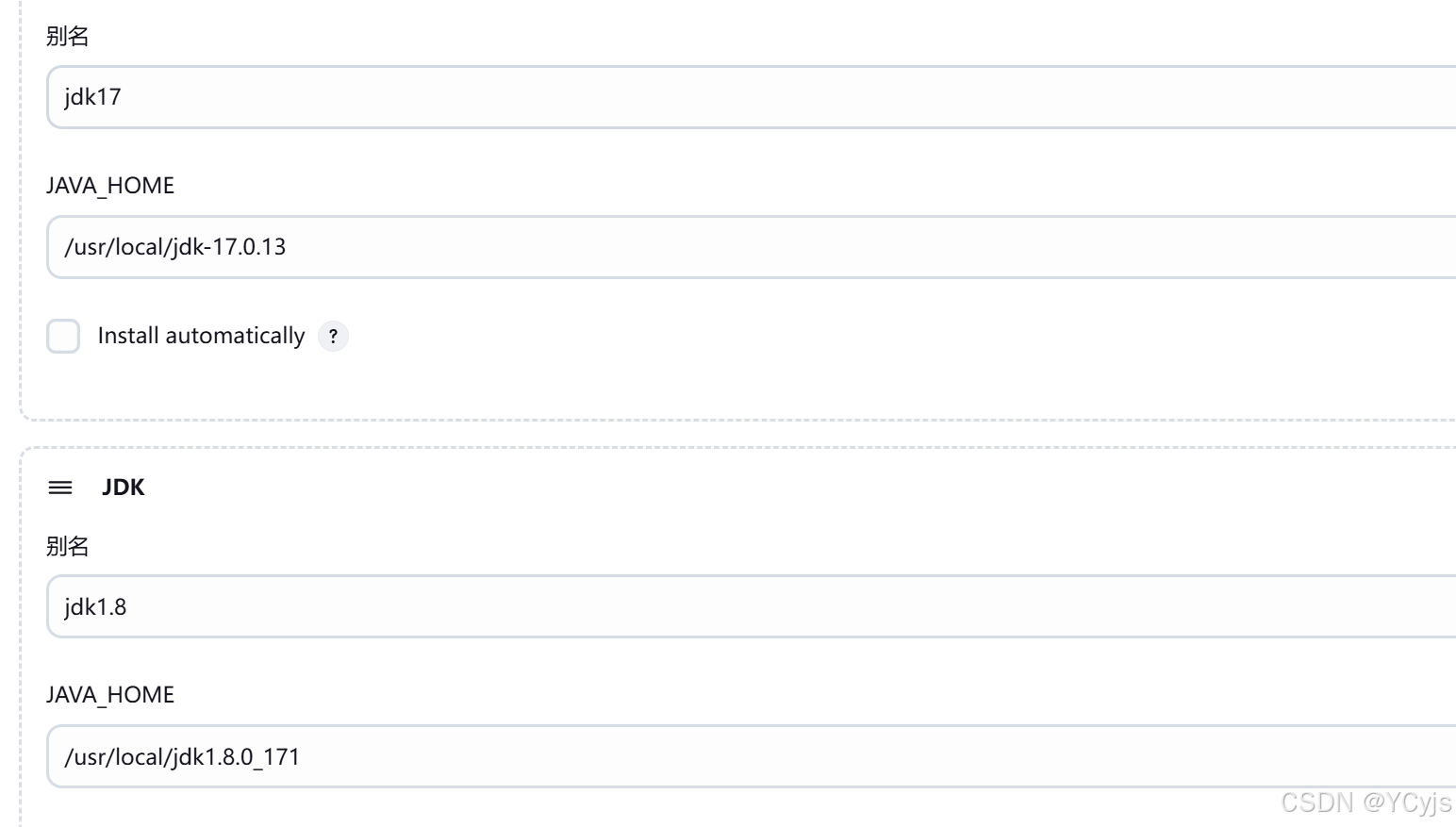
点击 新增JDK,别名输入 jdk17,取消勾选 Install automatically,JAVA_HOME输入/usr/local/jdk-17.0.13/
点击 新增JDK,别名输入 jdk1.8,取消勾选 Install automatically,JAVA_HOME输入 /usr/local/jdk1.8.0_171/
点击 新增Maven,Name输入 maven3,取消勾选 Install automatically,MAVEN_HOME驶入 /usr/local/maven

点击 "应用"和"保存"。
添加 Jenkins 全局变量,让 Jenkins 能够识别 JDK 和 Maven 环境的命令
Manage Jenkins -> Configure System -> 全局属性,勾选 Environment variables
键值对列表添加:键 JAVA_HOME ,值 /usr/local/jdk-17.0.13/
键 M2_HOME ,值 /usr/local/maven
键 PATH+EXTRA ,值 $M2_HOME/bin

修改 Maven 的 settings.xml
先创建本地仓库目录
mkdir /root/repo
可以先备份一个
cd /usr/local/maven/conf/
cp settings.xml{,_bak}
vim /usr/local/maven/conf/settings.xml
放到注释外边
53 --> #本地仓库改为 /root/repo/
<localRepository>/root/repo</localRepository>
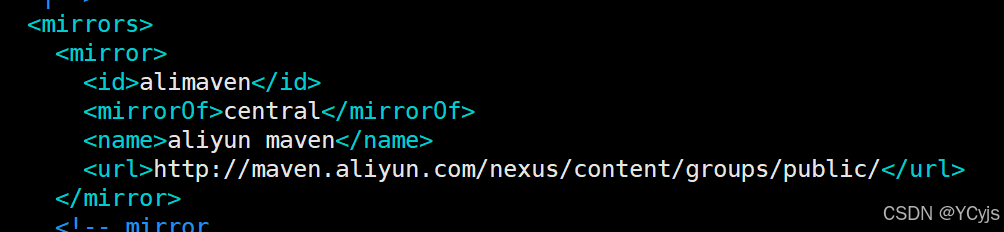
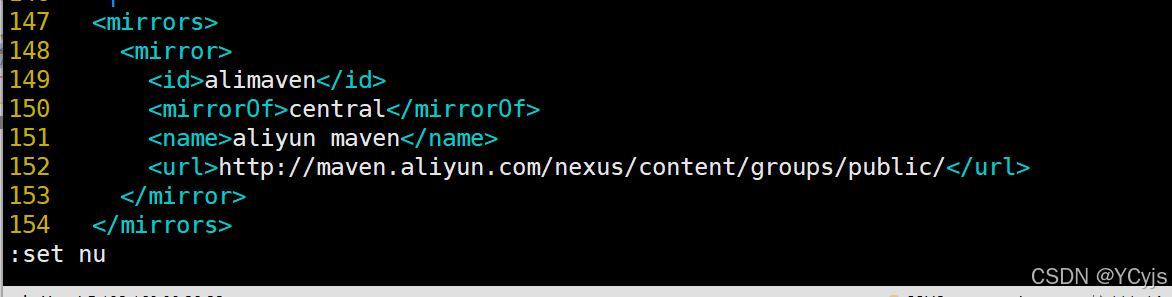
153 --> #添加阿里云私服地址
<mirror>
<id>alimaven</id>
<mirrorOf>central</mirrorOf>
<name>aliyun maven</name>
<url>http://maven.aliyun.com/nexus/content/groups/public/</url>
</mirror>
测试 Maven 是否配置成功
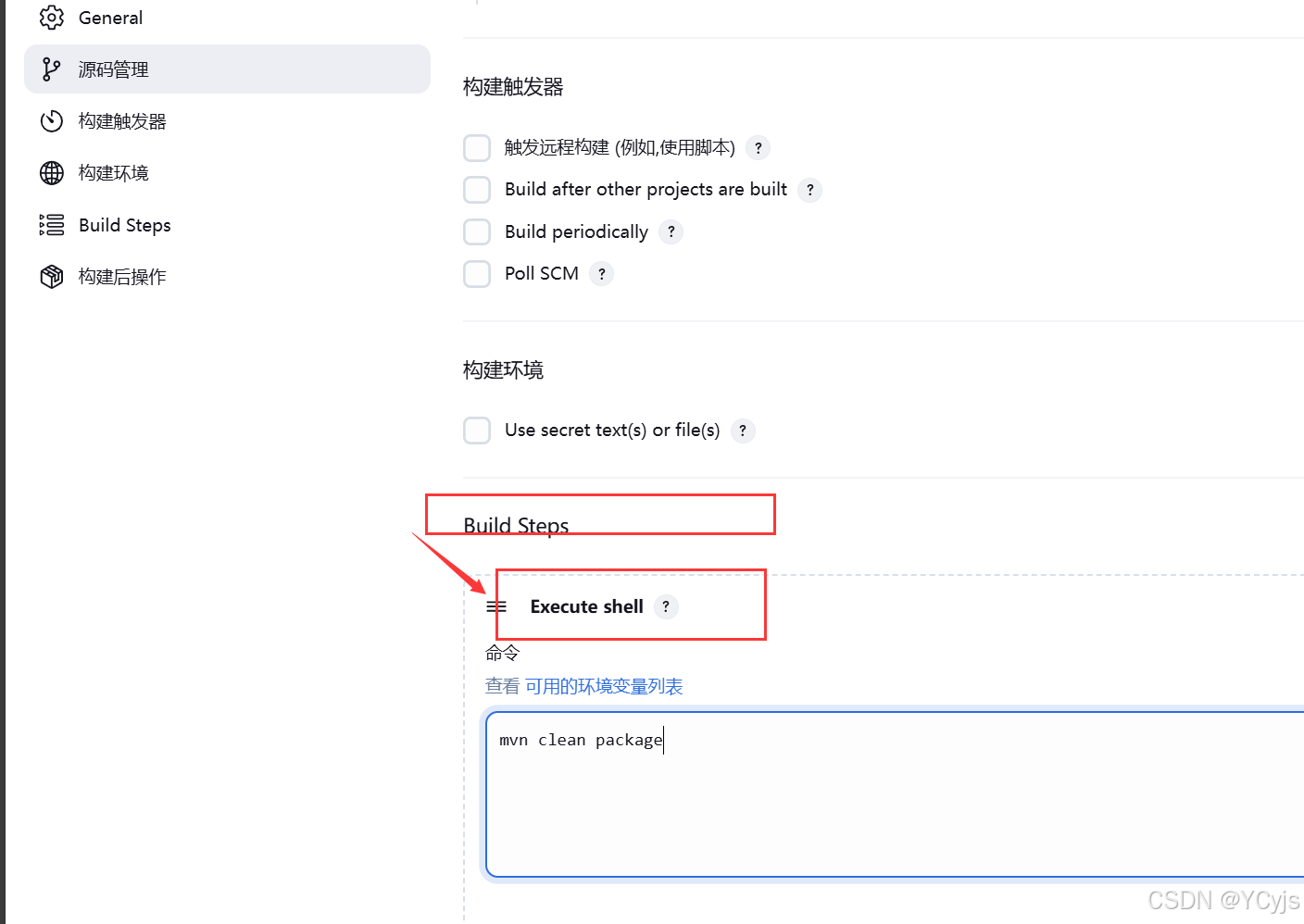
点击项目 test02 -> 设置 -> 构建 -> 增加构建步骤 -> Execute Shell
输入 mvn clean package
清空原有的构建元素(插件、依赖包等target文件),再进行打包
点击 保存
再次构建,如果可以把项目打成 war 包,代表 maven 环境配置成功。
补充:查看错误
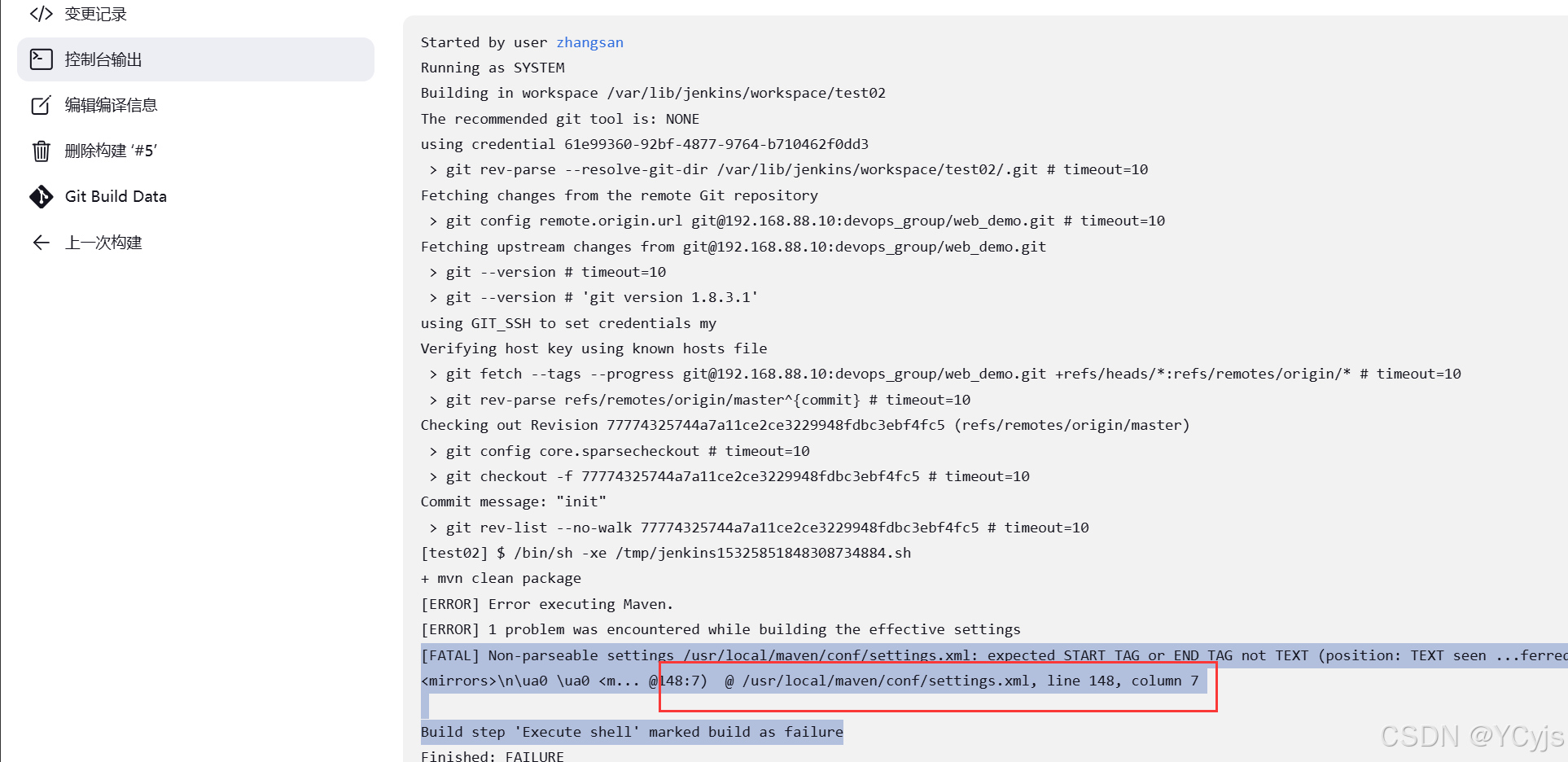
vim /usr/local/maven/conf/settings.xml
<mirrors>
<mirror>
<id>alimaven</id>
<mirrorOf>central</mirrorOf>
<name>aliyun maven</name>
<url>http://maven.aliyun.com/nexus/content/groups/public/</url>
</mirror>
</mirrors>
还有一个错误(开发的错误)我们在gitlab中修改

<project xmlns="http://maven.apache.org/POM/4.0.0" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance" xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
<modelVersion>4.0.0</modelVersion>
<!-- 项目坐标 -->
<groupId>com.itheima</groupId>
<artifactId>web_demo</artifactId>
<version>1.0-SNAPSHOT</version>
<packaging>war</packaging>
<!-- 依赖项 -->
<dependencies>
<dependency>
<groupId>javax.servlet</groupId>
<artifactId>servlet-api</artifactId>
<version>2.5</version>
</dependency>
</dependencies>
<!-- 构建配置 -->
<build>
<plugins>
<!-- maven-war-plugin 插件 -->
<plugin>
<groupId>org.apache.maven.plugins</groupId>
<artifactId>maven-war-plugin</artifactId>
<version>3.3.2</version>
</plugin>
</plugins>
</build>
</project>
最终
cd /var/lib/jenkins/workspace/test02/target

3.5、Tomcat 安装和配置
测试机30
apache-tomcat-8.5.16.tar.gz和jdk-8u171-linux-x64.tar.gz放到opt,
1、安装 Tomcat8.5
tar zxvf jdk-8u171-linux-x64.tar.gz -C /usr/local/
vim /etc/profile
export JAVA_HOME=/usr/local/jdk1.8.0_171
export JRE_HOME=${JAVA_HOME}/jre
export CLASSPATH=.:${JAVA_HOME}/lib:${JRE_HOME}/lib
export PATH=${JAVA_HOME}/bin:${JRE_HOME}/bin:$PATHsource /etc/profile
tar zxvf apache-tomcat-8.5.16.tar.gz
mv /opt/apache-tomcat-8.5.16/ /usr/local/tomcat
/usr/local/tomcat/bin/startup.sh
2、配置 Tomcat 用户角色权限
默认情况下 Tomcat 是没有配置用户角色权限的
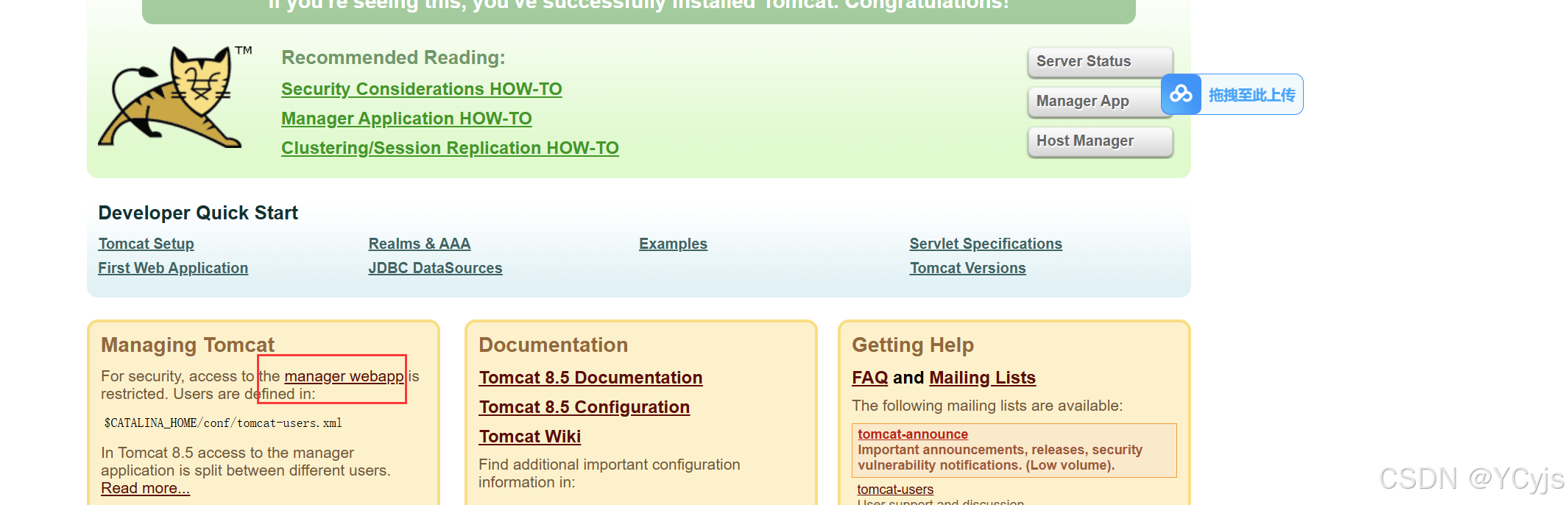
验证方法:可浏览器访问http://192.168.88.30:8080 ,点击 Managing Tomcat 下的 manager webapp ,发现返回 403 页面。
但是后续 Jenkins 部署项目到 Tomcat 服务器,需要用到 Tomcat 的用户进行远程部署,所以修改 tomcat 以下配置,添加用户及权限
vim /usr/local/tomcat/conf/tomcat-users.xml
43 行添加 tomcat 用户角色权限,指定用户和密码都是 tomcat ,并授予权限
<role rolename="tomcat"/>
<role rolename="role1"/>
<role rolename="manager-script"/>
<role rolename="manager-gui"/>
<role rolename="manager-status"/>
<role rolename="admin-gui"/>
<role rolename="admin-script"/>
<user username="tomcat" password="tomcat" roles="manager-gui,manager-script,tomcat,admin-gui,admin-script"/>
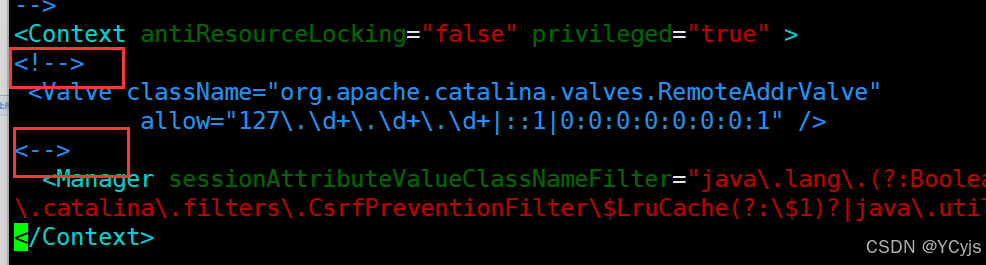
</tomcat-users>vim /usr/local/tomcat/webapps/manager/META-INF/context.xml
<!-- #注释掉 Valve 配置
<Valve className="org.apache.catalina.valves.RemoteAddrValve"
allow="127\.\d+\.\d+\.\d+|::1|0:0:0:0:0:0:0:1" />
-->
/usr/local/tomcat/bin/shutdown.sh
/usr/local/tomcat/bin/startup.sh
再次访问:http://192.168.88.30:8080/manager/html,输入账号/密码 tomcat/tomcat,即可成功登录
四、Jenkins 构建 Maven 项目风格
Jenkins 自动构建项目的类型有很多,常用的有以下三种:
1、自由风格软件项目(FreeStyle Project)
可以构建很多不同语言的项目,Jenkins 默认提供的构建类型,新手
2、Maven 项目(Maven Project)
专门针对 java 语言的 Maven 项目来进行构建,在构建 Maven 项目会比较方便
3、流水线项目(Pipeline Project)
使用代码的形式编写构建过程,灵活度非常高
每种类型的构建其实都可以完成一样的构建过程与结果,只是在操作方式、灵活度等方面有所区别,在实际开发中可以根据自己的需求和习惯来选择。
4.1、自由风格项目构建
项目的集成过程:拉取代码 -> 编译 -> 打包 -> 部署
拉取代码
新建item -> 任务名称(web_demo_freestyle) FreeStyle Project -> 确定
源码管理:选择 Git,Repository URL:git@192.168.88.10:devops_group/web_demo.git
Credentials 下拉选择 gitlab-auth-ssh,点击 保存
点击 Build Now,尝试构建项目
编译打包
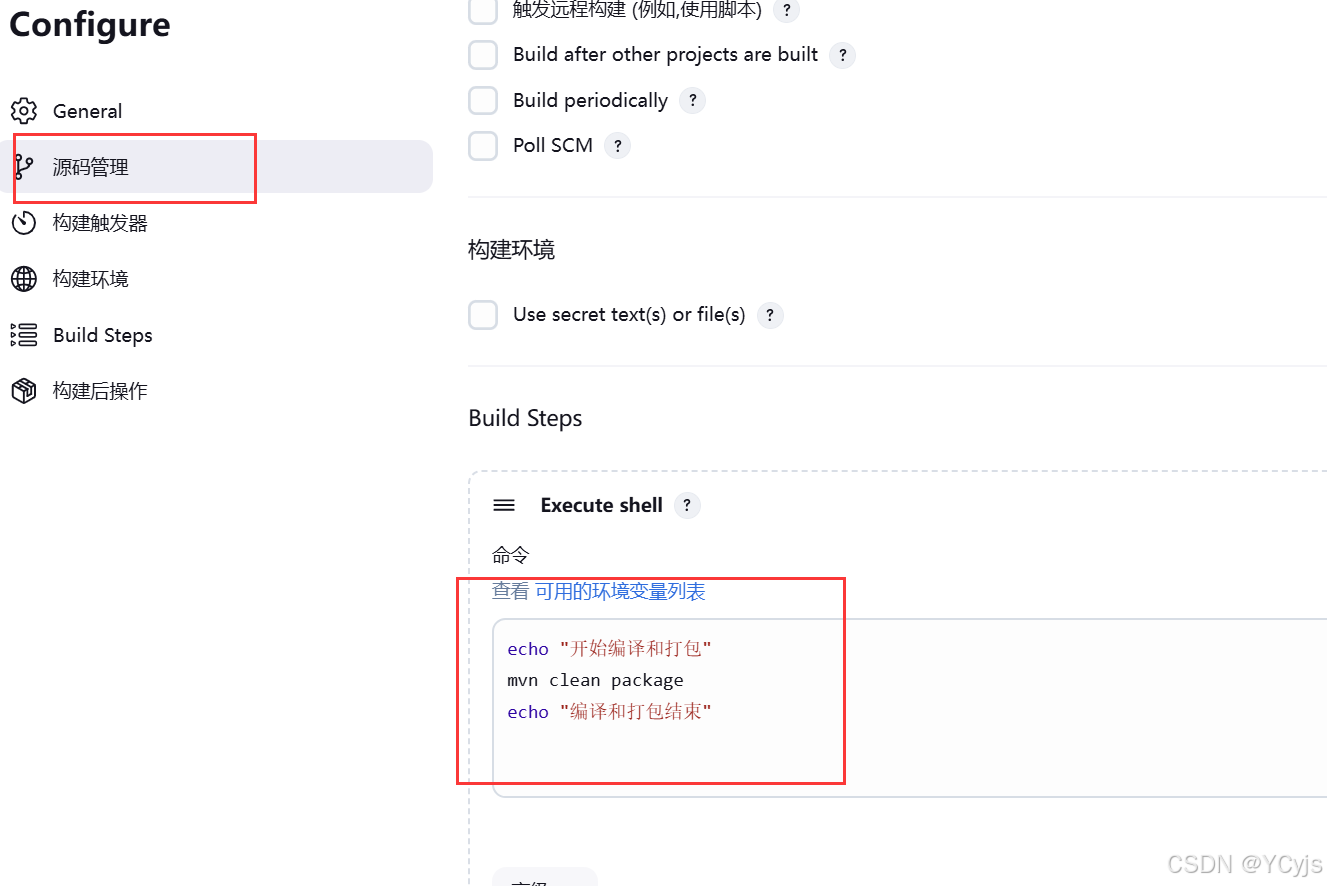
配置 —> 构建 -> 添加构建步骤 -> Execute Shell,输入以下命令
echo "开始编译和打包"
mvn clean package
echo "编译和打包结束"
点击 Build Now,尝试构建项目
把项目部署到远程的 Tomcat 里面
1、安装 Deploy to container 插件
远程安装到tomcat的功能
Jenkins 本身无法实现远程部署到 Tomcat 的功能,需要安装 Deploy to container 插件实现:
Manage Jenkins -> 管理插件-可选插件 -> 搜索 Deploy to container 插件选中直接安装即可
2、添加构建后操作
配置 —> 构建后操作 -> 增加构建后操作步骤 -> Deploy war/ear to a container
WAR/EAR files 输入 target/*.war
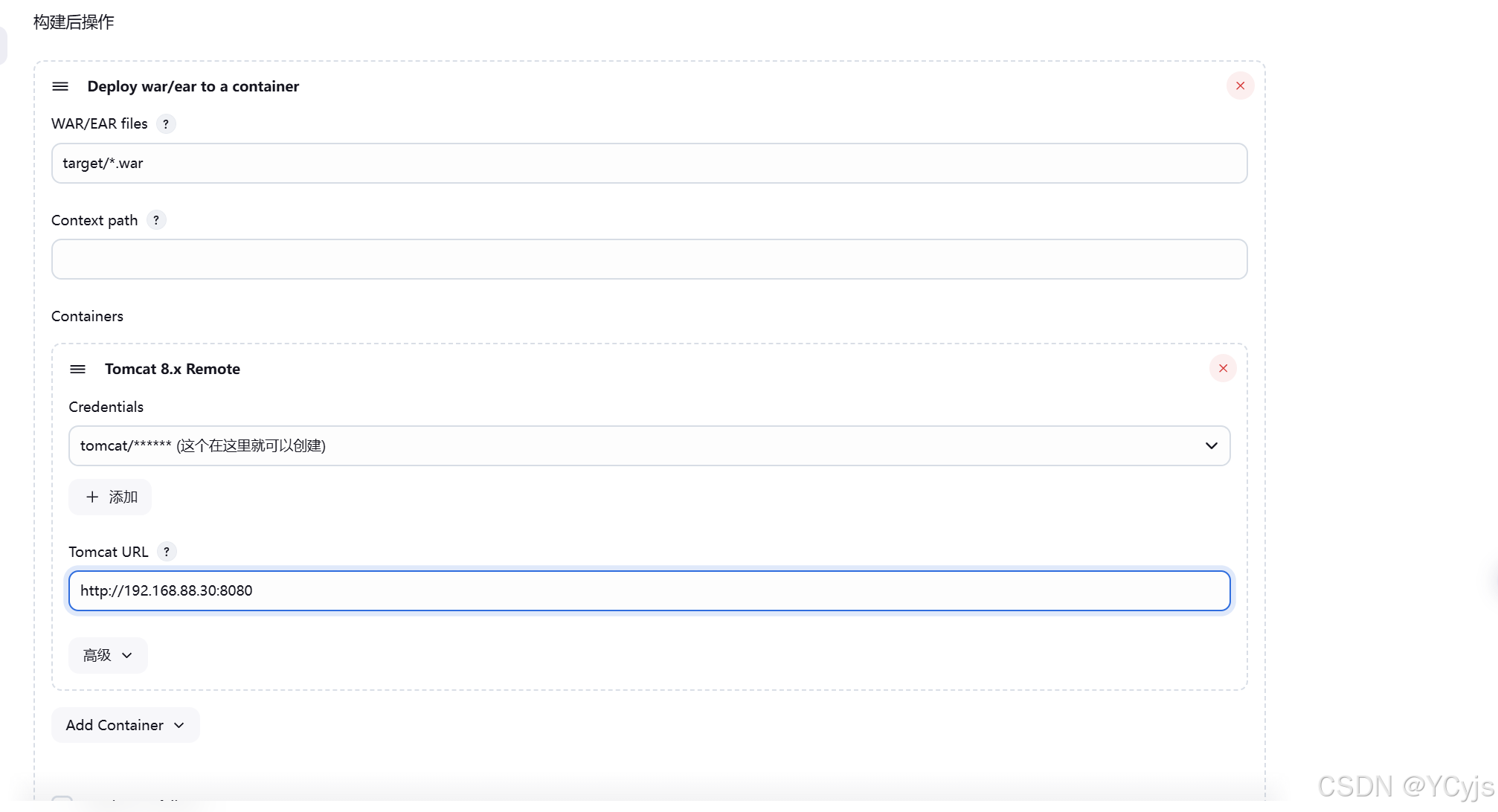
Containers —> Add Container —> Tomcat 8.x Remote -> Credentials,点击添加 -> Jenkins
用户名 输入 tomcat,密码 输入 tomcat,描述 输入 tomcat-auth,点击添加
3、Credentials 下拉选择 tomcat-auth
Tomcat URL 输入 http://192.168.88.30:8080
点击保存
点击 Build Now,尝试构建项目
4、部署成功后,刷新 http://192.168.88.30:8080/manager/html 页面,可以发现应用程序中多出一个项目,点击新项目进去访问


4.2、Maven项目构建
在gitable,10号机器运行
1、修改源码并提交到 gitlab
cd /root/web_demo
vim src/main/webapp/index.jsp
<%@ page contentType="text/html;charset=UTF-8" language="java" %>
<html>
<head>
<title>演示项目主页</title>
</head>
<body>
如果看到此页面,代表项目部署成功啦!
<hr/> #添加
<a href="/addUser">添加用户</a> #添加
</body>
</html>git add .
git commit -m "添加用户"
git push -u origin master
账号/密码:zhangsan/zhangsan@123
2、安装 Maven Integration 插件
Manage Jenkins -> 管理插件-可选插件 -> 搜索 Maven Integration 插件选中直接安装即可
3、创建 Maven 项目
新建item -> 任务名称(web_demo_maven) 构建一个maven项目 -> 确定
源码管理:选择 Git,Repository URL:git@192.168.80.10:devops_group/web_demo.git
Credentials 下拉选择 gitlab-auth-ssh,点击 保存
Build:Root POM 输入 pom.xml #指定 pom.xml 文件的路径
Goals and options 输入 clean package #输入 maven 指令,不用写 mvn
构建后操作:增加构建后操作步骤 -> Deploy war/ear to a container
WAR/EAR files 输入 target/*.war
Containers —> Add Container —> Tomcat 8.x Remote -> Credentials 下拉选择 tomcat-auth
Tomcat URL 输入 http://192.168.88.30:8080
点击保存
点击 Build Now,尝试构建项目
浏览器访问项目:http://192.168.88.30:8080/web_demo-1.0-SNAPSHOT/
五、
六、
七、
八、
九、附加
软件开发生命周期(SDLC)
| 阶段 | 描述 |
|---|---|
| 需求分析 | 这是SDLC的第一阶段。项目团队根据内部需求或客户需求执行可行性分析。此阶段主要收集信息,可能是对现有项目的改进或开发新项目。同时,分析项目的预算、预期收益和总体布局,明确项目创建的目标。 |
| 设计 | 第二阶段是设计阶段,涉及系统架构的规划、确定产品应达到的状态(即产品的外观和功能),并创建项目计划。计划可以通过图表、布局设计或文字形式呈现,确保团队成员对项目有清晰的理解。 |
| 实现 | 在实现阶段,项目经理创建任务并分配给开发者。开发者根据分配的任务和在设计阶段定义的目标进行代码开发。根据项目的大小和复杂性,此阶段可能需要数月或更长时间才能完成。 |
| 测试 | 测试阶段是确保产品质量的关键环节。测试人员执行各种测试,包括功能测试(验证产品是否按预期工作)、代码测试(检查代码质量和性能)、压力测试(评估产品在极端条件下的表现)等。这些测试有助于发现潜在的问题并进行修复。 |
| 进化/维护 | 最后阶段是产品的持续改进和维护。根据用户反馈和使用情况,可能需要对产品进行功能修改、bug修复或功能增加。此阶段确保产品持续满足用户需求,并保持其竞争力和市场地位。 |
CI/CD流程表格
什么是ci
频繁地(一天多次)将代码集成到主干。
持续集成的目的,就是让产品可以快速迭代,同时还能保持高质量。它的核心措施是,代码集成到主干 之前,必须通过自动化测试。只要有一个测试用例失败,就不能集成。
什么是CD
持续交付(Continuous Delivery)
在持续集成的基础上,持续交付实现了自动化测试和构建流程,使得新版本软件可以快速、有效、安全地部署到生产环境。
虽然自动化可以发布代码,但实际的发布操作可能需要人为确认和审批。
持续交付(Continuous Delivery)
CD也代表持续部署,这是持续交付的进一步扩展。
在持续部署中,不仅自动化了测试和构建过程,还自动化了部署过程。
这意味着每次代码变更都能自动部署到生产环境,无需人工审批,从而确保了软件的最新版本总是在生产环境中。
| 类别 | 流程/概念 | 描述 |
|---|---|---|
| CI(持续集成) | 提交,代码合并 | 开发人员提交新代码后,将其合并到主干或主分支中 |
| 构建 | 自动构建过程,从检出代码到编译构建,无需人工干预 | |
| 部署 | 将构建后的代码部署到指定的测试环境中 | |
| 测试 | 运行自动化测试,包括单元测试、集成测试等,确保新代码与原有代码正确集成 | |
| 反馈 | 根据测试结果提供反馈,决定是否允许代码集成到主干 | |
| 组成要素 | 自动构建过程 | 自动完成从检出代码到测试统计的全过程 |
| 代码存储库 | 使用版本控制软件(如SVN、Git)存储代码,作为构建过程的素材库 | |
| 持续集成服务器 | 如Jenkins,用于配置和管理持续集成过程 | |
| 好处 | 降低风险 | 早期发现问题,减少修复代价 |
| 持续检查 | 对系统健康进行持续检查,减少发布风险 | |
| 减少重复性工作 | 自动化过程减少手动操作 | |
| 持续部署 | 提供可部署单元包,支持快速迭代 | |
| 持续交付 | 提供可供使用的版本,加速产品交付 | |
| 增强团队信心 | 通过自动化测试和持续集成,提高团队对产品质量和进度的信心 | |
| CD(持续交付与持续部署) | 持续交付 | 将集成后的代码部署到更贴近真实运行环境的“类生产环境”中,准备发布 |
| 部署到测试环境 | 在测试环境中进行进一步的验证和测试 | |
| 部署到预生产环境 | 在预生产环境中进行最终的验证和测试,确保系统稳定性 | |
| 持续部署 | 将最终产品自动化部署到生产环境,供用户使用 | |
| 区分 | 持续部署意味着所有变更自动部署到生产环境;持续交付意味着所有变更可以部署到生产环境,但可以选择不部署 |
CI/CD 流程表
| 阶段 | 描述 | 工具与技术 |
|---|---|---|
| 1. 代码提交 | 开发人员将代码提交到版本控制系统(如 Git)。 | Git, SVN |
| 2. 持续集成(CI) | 开发人员提交代码后,CI 系统(如 Jenkins)自动触发构建、测试等流程,确保代码集成正常。每次提交都需进行自动化构建和测试,确保新代码与现有代码无冲突。 | Jenkins, GitLab CI, Travis CI, CircleCI |
| 3. 自动构建 | CI 服务器自动拉取最新的代码,进行编译、构建等操作。构建过程通常包括代码编译、静态分析、单元测试等。 | Maven, Gradle, Ant, Webpack |
| 4. 单元测试 | 自动执行单元测试,验证新代码是否与现有代码兼容,并保证基本功能正常。若单元测试失败,则停止流程,不允许代码合并。 | JUnit, TestNG, Mocha, Jest |
| 5. 测试报告 | 测试结果生成报告并反馈给开发人员,显示成功与失败的用例,帮助开发人员定位问题并及时修复。 | Allure, Jenkins test reports, SonarQube |
| 6. 代码质量检查 | 代码质量自动检查(如静态分析),确保代码遵循编码规范,避免引入技术债务。 | SonarQube, Checkstyle, ESLint |
| 7. 部署到测试环境 | 将构建好的代码自动部署到测试环境,进行功能、集成等测试。 | Docker, Kubernetes, Ansible, Terraform |
| 8. 持续交付(CD) | 自动将通过测试的代码部署到更接近生产环境的预生产环境(Staging)。目标是能够随时提供一个可交付的版本。此阶段的重点是快速、高频地交付新的功能或修复。 | Jenkins, GitLab CI, ArgoCD, Spinnaker |
| 9. 用户验证 | 在预生产环境中,产品经理或 QA 团队验证新功能是否符合需求。 | TestRail, Jira, Azure DevOps |
| 10. 部署到生产环境 | 在生产环境自动部署经过验证的版本,确保产品能够在用户端使用。 | Kubernetes, Docker, Helm, AWS ECS, Azure DevOps |
| 11. 持续部署(CD) | 所有变更都被自动部署到生产环境,不需要人工干预。持续部署要求代码始终处于可发布状态,任何成功通过的构建都会自动进入生产环境。 | Jenkins, CircleCI, GitHub Actions, ArgoCD |
| 12. 监控与反馈 | 在生产环境中持续监控系统的运行状态,收集用户反馈,及时响应问题。 | Prometheus, Grafana, ELK Stack, New Relic |
| 13. 问题修复与优化 | 根据监控和用户反馈,开发人员快速修复问题并进行性能优化。继续进行 CI/CD 流程,保持迭代的节奏。 | Git, Jira, Slack |
关键概念
-
持续集成(CI):
- 目的是尽早发现集成问题,每次代码提交后立即构建、测试,并反馈结果。通过自动化测试和构建,确保代码质量和集成的稳定性。
- 自动化构建:包括从代码检出、编译、单元测试到生成构建产物的全过程。
- 自动化测试:确保新代码与现有代码无冲突,功能不受影响。
-
持续交付(CD):
- 在持续集成的基础上,自动化部署到类生产环境(如预生产环境),确保软件能在生产环境之前经过充分测试。
- 目标是快速交付高质量的软件版本。
-
持续部署(CD):
- 所有通过测试的变更都会自动部署到生产环境,确保每个成功的构建都能快速且可靠地投入使用。
- 与持续交付的区别:持续交付可以选择是否部署到生产,而持续部署则是将所有变更自动发布到生产环境。
好处与目标
- 提高代码质量:通过自动化测试和构建,减少人为错误。
- 降低发布风险:通过频繁、小规模的更新,降低大版本发布的风险。
- 提高开发效率:自动化流程减少重复工作,增加开发团队的专注度。
- 快速反馈与修复:通过持续集成与交付,开发人员能够快速收到测试反馈并进行修复,减少问题积累。
- 增强团队信心:通过持续集成和自动化部署,团队能够快速验证新功能,保持高质量和稳定性。