大家好,作为一个在Windows系统下摸爬滚打多年的职场人士,我发现,选择对的办公软件真的能大大提升工作效率。今天,就来给大家推荐5款装机必备的办公软件,让你轻松应对各种工作挑战!
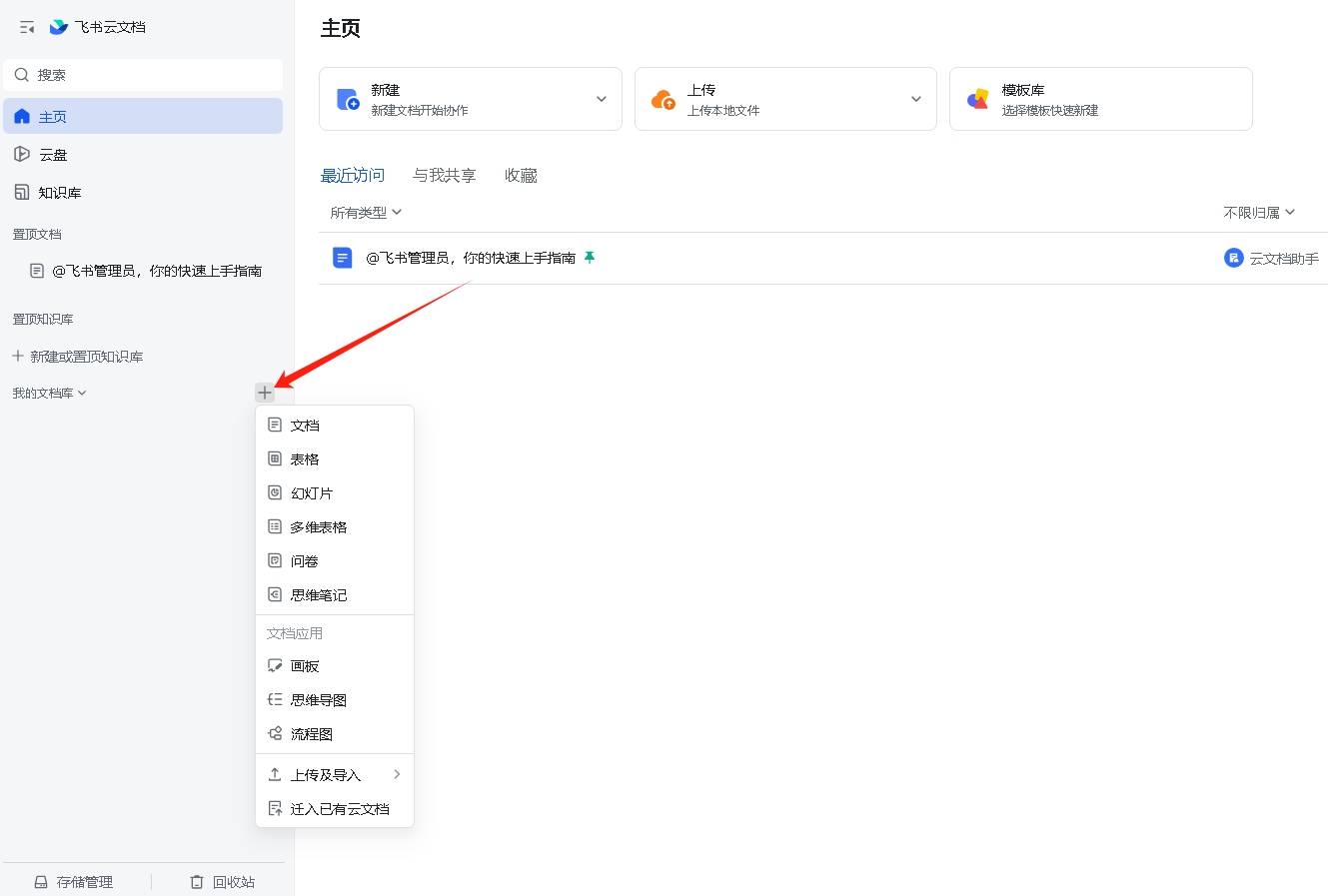
1、办公软件:飞书office
不仅提供了强大的文档、表格、幻灯片等基础办公功能,还融入了即时通讯、日程管理、在线协作等功能。这意味着,你无需切换多个软件,即可实现文件的编辑、分享、讨论和审批。
界面简洁直观,操作流畅,对于习惯了传统Office的用户来说,上手也毫无压力。
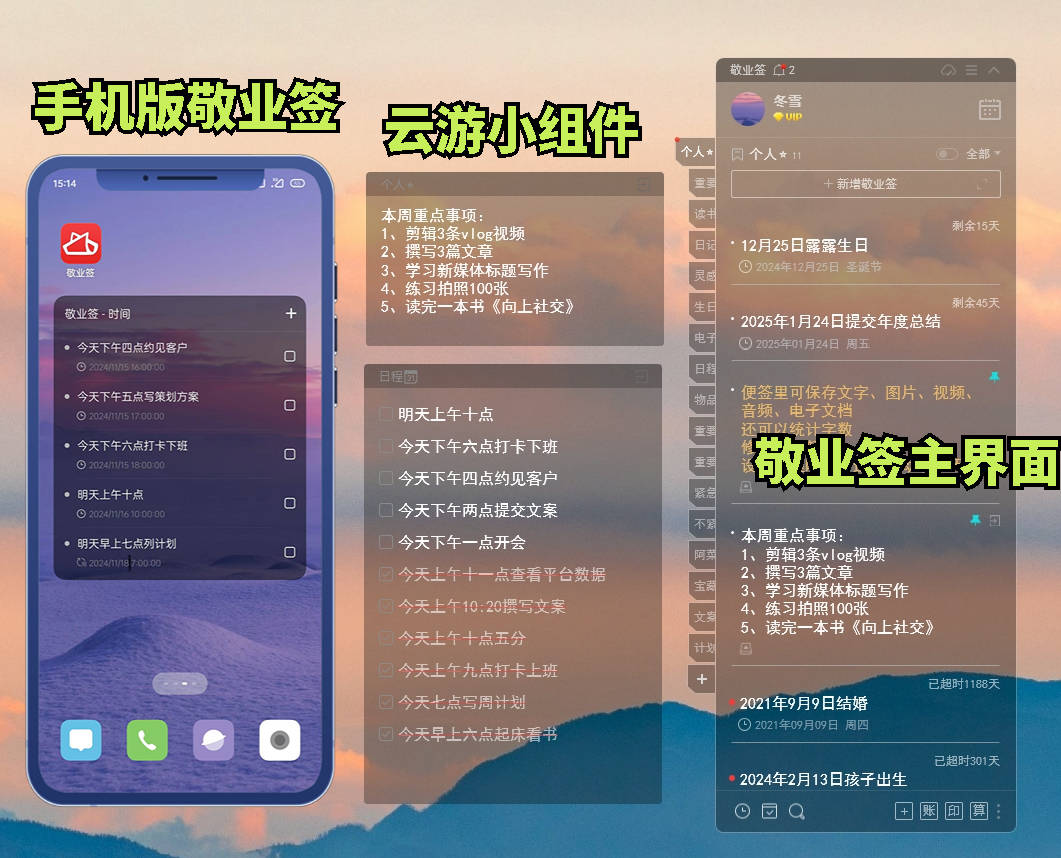
2、桌面便签待办:敬业签
它是一款能帮你高效管理时间和任务的桌面便签软件。便签里支持多种记录方式,如文字、图片、录音、文档等,让你可以根据自己的喜好和习惯来记录重要事项。支持多端同步,无论是电脑、手机还是iPad,都能实时查看和更新你的待办清单。
界面简洁,功能实用,特别是其提醒功能,可以设置单次提醒、重复提醒、农历提醒等多种提醒方式,确保你不会错过任何一个重要的时间节点。
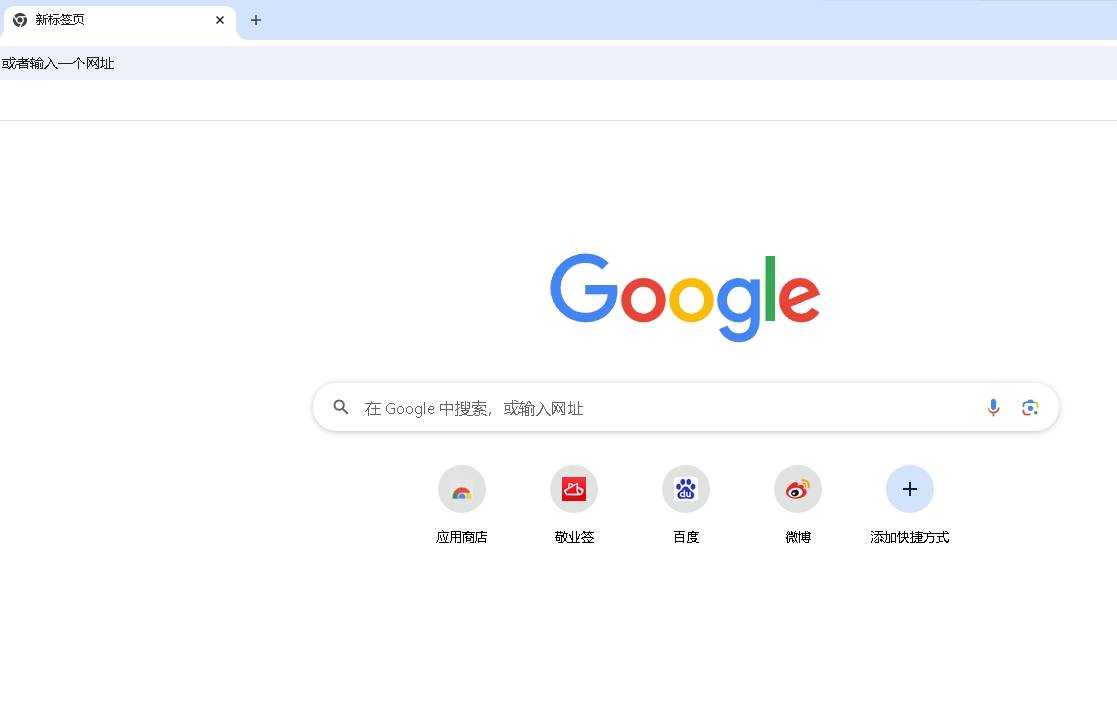
3、浏览器:Google Chrome
提到浏览器,谷歌浏览器受到了很多职场人士的青睐。它不仅拥有强大的搜索功能和丰富的扩展插件,还具备出色的兼容性和稳定性。无论是浏览网页、观看视频、还是进行在线办公,Chrome都能提供流畅、快速的体验。
特别是对于经常需要访问多个网页的用户来说,Chrome的多标签页功能和快捷键操作无疑大大提升了工作效率。
4、截图软件:pixpin
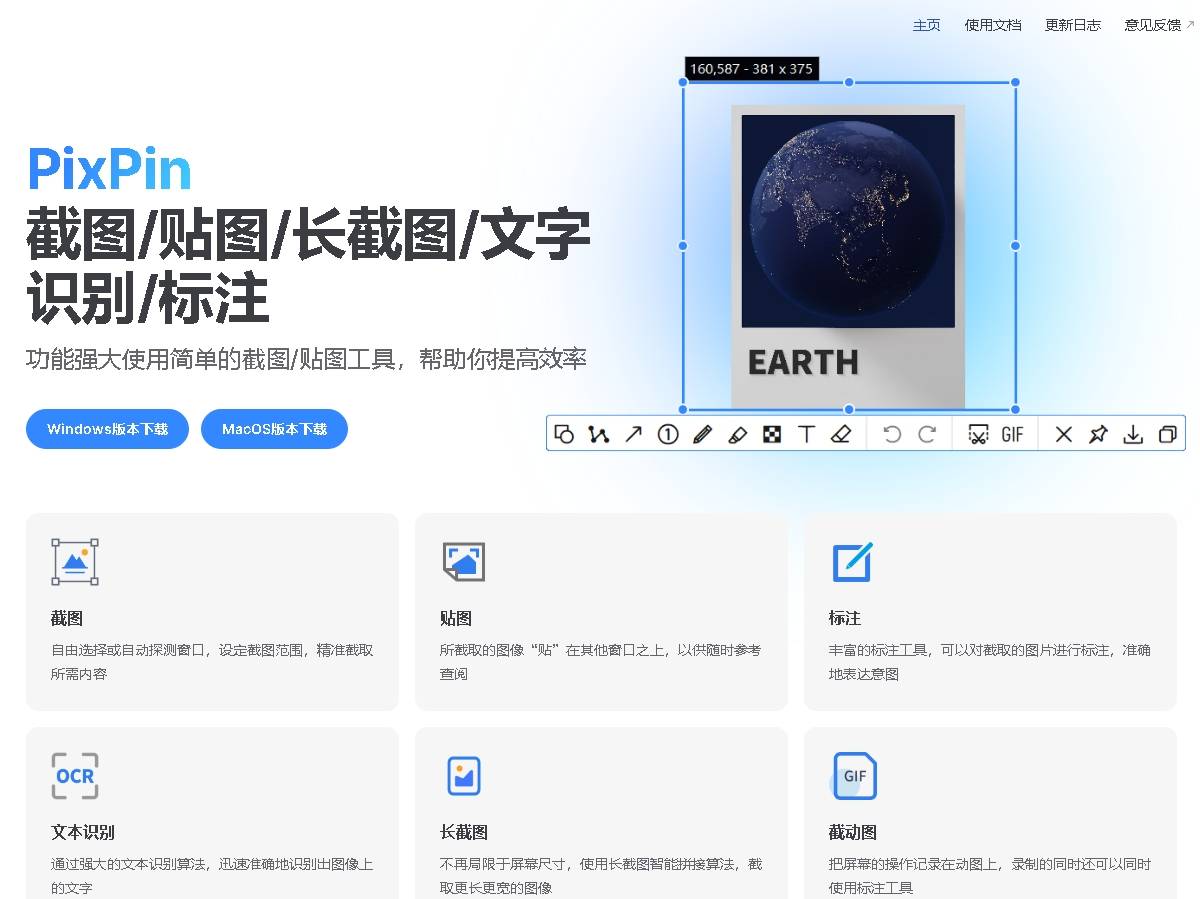
在日常工作中,截图是一项非常频繁的操作。PixPin作为一款专业的截图软件,不仅支持全屏、窗口、区域等多种截图方式,还提供了丰富的编辑功能,如标注、涂鸦、文字添加等,让你轻松制作出专业级的截图。
支持滚动截屏,识别图片中的文字等,非常实用。
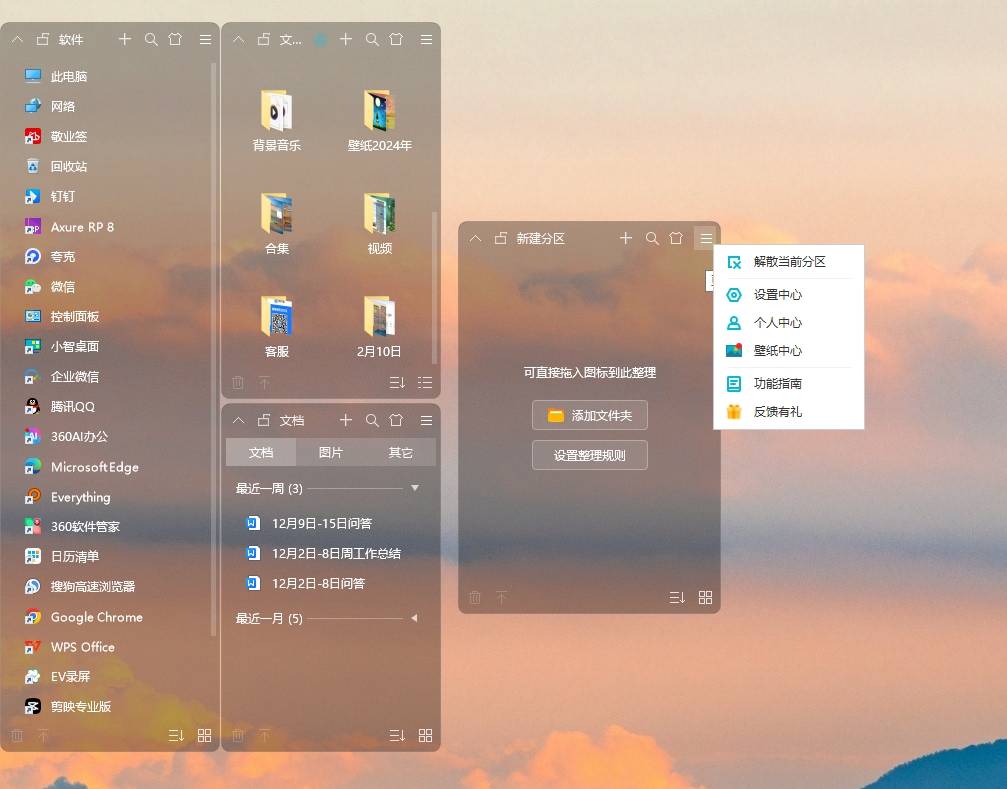
5、桌面整理:小智桌面
小智桌面能够帮助用户快速整理杂乱无章的电脑桌面。它可以自动对桌面上的文件、文件夹和快捷方式进行智能分类,例如将文档类文件归为一类、图片类归为一类、应用程序快捷方式归为一类等,使桌面瞬间变得整洁有序。
大家还可以根据自己的使用习惯手动创建不同的桌面分区,将相关的文件和快捷方式拖放到对应的分区中,进一步优化桌面布局,提高文件查找和应用程序启动的效率。