题目大意
有一个 \(n\times m\) 的花园,\(a_{i,j}=1\) 表示可以种花,\(a_{i,j}=0\) 表示不可以种花,请求出有多少种种花的的方案,使得形成 C 或 F 的形状,\(n,m\le 10^3\)。
思路分析
观察 C 和 F,发现 F 可以认为是 C 的左下角加一笔竖画,所以先求 C。
求形成 C 的方案数
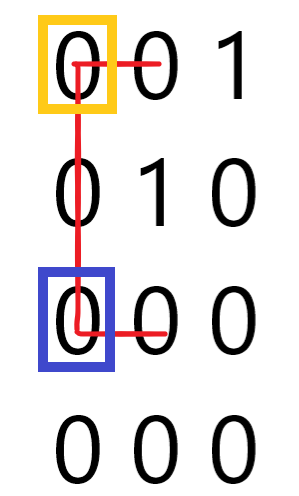
枚举 C 的左上角的点和左下角的点,即枚举第 \(j\) 列,黄色点在这一列的第 \(x\) 行,蓝色点在这一列的第 \(y\) 行,然后计算一下黄色点能往右延伸几格,蓝色点能往右延伸几格,相乘即可。这一步可以用后缀和 \(r_{i,j}\) 来实现。
for(int i=1;i<=n;i++){
for(int j=m;j>=1;j--){
if(a[i][j]=='1'){
r[i][j]=0;
}else{
r[i][j]=r[i][j+1]+1;
}
}
}
for(int j=1;j<=m;j++){
for(int x=1;x<=n;x++){
for(int y=x+2;y<=n;y++){
if(a[x][j]=='1'){
break;
}
ansc=ansc+(r[x][j]-1)*(r[y][j]-1);
}
}
}
计算时 \((r_{x,j}-1)\times(r_{y,j}-1)\) 不好看,所以预处理后缀和后非 \(0\) 的 \(r_{i,j}\) 都减去 \(1\) 就行了。
for(int i=1;i<=n;i++){
for(int j=m;j>=1;j--){
if(a[i][j]=='1'){
r[i][j]=0;
}else{
r[i][j]=r[i][j+1]+1;
}
}
}
for(int i=1;i<=n;i++){
for(int j=m;j>=1;j--){
if(r[i][j]!=0){
r[i][j]--;
}
}
}
for(int j=1;j<=m;j++){
for(int x=1;x<=n;x++){
for(int y=x+2;y<=n;y++){
if(a[x][j]=='1'){
break;
}
ansc=ansc+r[x][j]*r[y][j];
}
}
}
后缀和时间复杂度为 \(\mathcal{O(nm)}\),计算的时间复杂度为 \(\mathcal{O(n^2m)}\),代码的时间复杂度为 \(\mathcal{O(n^2m)}\),超时。
继续观察计算的三重循环,发现计算时只有 \(r_{y,j}\) 发生变化,可以再用一个后缀和维护后缀和 \(r_{i,j}\),记为 \(suf_{i,j}\),省去第三重循环 \(y\)。
for(int i=n;i>=1;i--){
for(int j=1;j<=m;j++){
suf[i][j]=suf[i+1][j]+r[i][j];
}
}
for(int j=1;j<=m;j++){
int lst=n+1;
for(int x=n;x>=1;x--){
if(a[x][i]=='1'){
lst=x;
continue;
}
if(lst<x+2){
continue;
}
ansc=ansc+(suf[x+2][i]-suf[lst][i])*r[x][i];
}
}
这样,时间复杂度降为 \(\mathcal{O(nm)}\),不超时。
求形成 C 的方案数
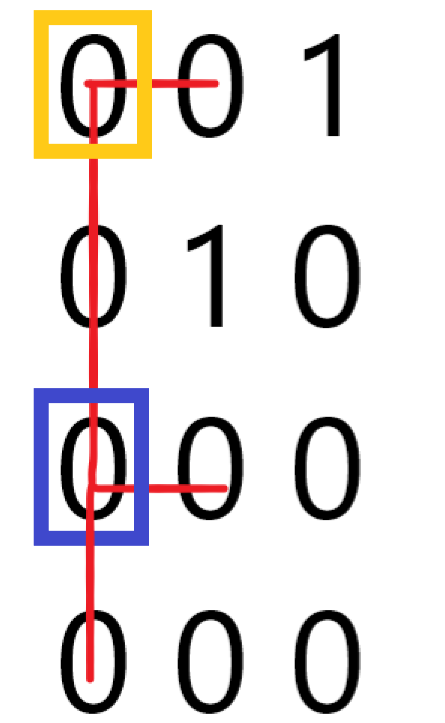
与 C 类似,同样先枚举 F 的左上角的点和第二条杠左边的点,即枚举第 \(j\) 列,黄色点在这一列的第 \(x\) 行,蓝色点在这一列的第 \(y\) 行,然后计算一下黄色点能往右延伸几格,蓝色点能往右延伸几格,还计算蓝色点能向下延伸格,相乘即可。向右和 C 的后缀和 \(r_{i,j}\) 相同,向下再用后缀和数组 \(d_{i,j}\) 实现。
for(int i=n;i>=1;i--){
for(int j=1;j<=m;j++){
if(a[i][j]=='1'){
d[i][j]=0;
}else{
d[i][j]=d[i+1][j]+1;
}
}
}
for(int i=n;i>=1;i--){
for(int j=1;j<=m;j++){
if(d[i][j]!=0){
d[i][j]--;
}
}
}
for(int j=1;j<=m;j++){
for(int x=1;x<=n;x++){
for(int y=x+2;y<=n;y++){
if(a[x][j]=='1'){
break;
}
ansf=ansf+r[x][j]*r[y][j]*d[y][j];
}
}
}
后缀和时间复杂度为 \(\mathcal{O(nm)}\),计算的时间复杂度为 \(\mathcal{O(n^2m)}\),代码的时间复杂度为 \(\mathcal{O(n^2m)}\),超时。
计算时有 \(r_{y,j}\times d_{y,j}\) 发生变化,可以再用一个后缀和维护 \(r_{i,j}\times d_{y,j}\),记为大 \(Suf_{i,j}\),省去第三重循环 \(y\)。
for(int i=n;i>=1;i--){
for(int j=1;j<=m;j++){
Suf[i][j]=Suf[i+1][j]+r[i][j]*d[i][j];
}
}
for(int i=1;i<=m;i++){
int lst=n+1;
for(int x=n;x>=1;x--){
if(a[x][i]=='1'){
lst=x;
continue;
}
if(lst<x+2){
continue;
}
ansf=ansf+(Suf[x+2][i]-Suf[lst][i])*r[x][i];
}
}
这样,时间复杂度降为 \(\mathcal{O(nm)}\),不超时。
最后,注意取模 \(998244353\),还有多测要清空,不开 long long 见祖宗。
\(\texttt{code}\)
/*Written by smx*/
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define QAQ cout<<"QAQ\n";
const int MAXN=1e3+5,inf=1e18,mod=998244353;
int n,m,C,F,ansc,ansf;
char a[MAXN][MAXN];
int r[MAXN][MAXN],suf[MAXN][MAXN],d[MAXN][MAXN],Suf[MAXN][MAXN];
void init(){
ansc=ansf=0;
for(int i=1;i<=n+1;i++){
for(int j=1;j<=m+1;j++){
r[i][j]=suf[i][j]=d[i][j]=Suf[i][j]=0;
}
}
}
signed main(){
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T,id;
cin>>T>>id;
while(T--){
init();
cin>>n>>m>>C>>F;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=m;j>=1;j--){
if(a[i][j]=='1'){
r[i][j]=0;
}else{
r[i][j]=r[i][j+1]+1;
}
}
}
for(int i=1;i<=n;i++){
for(int j=m;j>=1;j--){
if(r[i][j]!=0){
r[i][j]--;
}
}
}
for(int i=n;i>=1;i--){
for(int j=1;j<=m;j++){
suf[i][j]=(suf[i+1][j]+r[i][j])%mod;
}
}
for(int i=1;i<=m;i++){
int lst=n+1;
for(int x=n;x>=1;x--){
if(a[x][i]=='1'){
lst=x;
continue;
}
if(lst<x+2){
continue;
}
ansc=(ansc+(suf[x+2][i]-suf[lst][i]+mod)%mod*r[x][i]%mod)%mod;
}
}
for(int i=n;i>=1;i--){
for(int j=1;j<=m;j++){
if(a[i][j]=='1'){
d[i][j]=0;
}else{
d[i][j]=d[i+1][j]+1;
}
}
}
for(int i=n;i>=1;i--){
for(int j=1;j<=m;j++){
if(d[i][j]!=0){
d[i][j]--;
}
}
}
for(int i=n;i>=1;i--){
for(int j=1;j<=m;j++){
Suf[i][j]=(Suf[i+1][j]+r[i][j]*d[i][j]%mod)%mod;
}
}
for(int i=1;i<=m;i++){
int lst=n+1;
for(int x=n;x>=1;x--){
if(a[x][i]=='1'){
lst=x;
continue;
}
if(lst<x+2){
continue;
}
ansf=(ansf+(Suf[x+2][i]-Suf[lst][i]+mod)%mod*r[x][i])%mod;
}
}
cout<<ansc*C%mod<<" "<<ansf*F%mod<<"\n";
}
return 0;
}