标签：精读 mathbf 论文 NGCF right LightGCN mathcal left

【论文精读】Lightgcn: Simplifying and powering graph convolution network for recommendation

链接：Lightgcn: Simplifying and powering graph convolution network for recommendation

年份：2020

引用数：3600+

关键词：推荐系统，图神经网络

目录

• 【论文精读】Lightgcn: Simplifying and powering graph convolution network for recommendation
  • 1. 对NGCF的消融实验
    • 1.1 什么是NGCF
    • 1.2 对NGCF的消融实验
  • 2. LightGCN
    • 模型流程
    • 矩阵形式
    • 损失函数
  • 3. 实验
  • 4. 个人评价

1. 对NGCF的消融实验

1.1 什么是NGCF

令\(\mathbf{e}_u^{(0)}\)表示初始时用户\(u\)的嵌入，\(\mathbf{e}_i^{(0)}\) 表示初始时物品\(i\)的嵌入。NGCF利用用户-物品交互图来传播嵌入，如下所示

\[\begin{aligned} & \mathbf{e}_u^{(k+1)}=\sigma\left(\mathbf{W}_1 \mathbf{e}_u^{(k)}+\sum_{i \in \mathcal{N}_u} \frac{1}{\sqrt{\left|\mathcal{N}_u\right|\left|\mathcal{N}_i\right|}}\left(\mathbf{W}_1 \mathbf{e}_i^{(k)}+\mathbf{W}_2\left(\mathbf{e}_i^{(k)} \odot \mathbf{e}_u^{(k)}\right)\right)\right), \\ & \mathbf{e}_i^{(k+1)}=\sigma\left(\mathbf{W}_1 \mathbf{e}_i^{(k)}+\sum_{u \in \mathcal{N}_i} \frac{1}{\sqrt{\left|\mathcal{N}_u\right|\left|\mathcal{N}_i\right|}}\left(\mathbf{W}_1 \mathbf{e}_u^{(k)}+\mathbf{W}_2\left(\mathbf{e}_u^{(k)} \odot \mathbf{e}_i^{(k)}\right)\right)\right), \end{aligned} \tag{1} \]

其中 \(e_u^{(k)}\) 和 \(e_i^{(k)}\) 分别表示用户 \(u\) 和项目 \(i\) 经过 \(k\) 层传播后的嵌入， \(\sigma\) 是非线性激活函数， \(\mathcal{N}_u\) 表示与用户 \(u\) 交互的项目集合， \(\mathcal{N}_i\) 表示与项目 \(i\) 交互的用户集合， \(W_1\) 和 \(W_2\) 是可训练的权重矩阵。传播 \(L\) 层后，NGCF 获得 \(L+1\) 个嵌入来描述一个用户 \(\left(e_u^{(0)}, e_u^{(1)}, \cdots, e_u^{(L)}\right)\)和一个项目 \(\left(e_i^{(0)}, e_i^{(1)}, \cdots, e_i^{(L)}\right)\) 。然后将这些 \(L+1\) 个嵌入连接起来，以获得最终的用户嵌入和项目嵌入，并使用内积生成预测分数。

1.2 对NGCF的消融实验

作者对NGCF做了消融实验，实现了三种简化的变体：

• NGCF-f,：移除了特征变换矩阵 \(\mathbf{W}_1\) ，\(\mathbf{W}_2\).
• NGCF-n：移除了非线性激活函数 \(\sigma\).
• NGCF-fn：同时移除了 \(\mathbf{W}_1\) ，\(\mathbf{W}_2\)和\(\sigma\).

实验结果如下

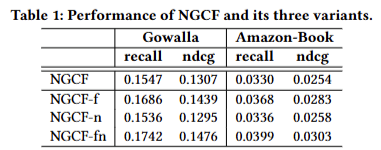
相对于NGCF，NGCF的分数得到了大幅提升。说明在NGCF中，特征变换和非线性激活是多余的。

2. LightGCN

模型流程

• 卷积（Light Graph Convolution，LGC）：

\[\left\{\begin{array}{l} e_u^{(k+1)}=\sum_{i \in \mathcal{N}_u} \frac{1}{\sqrt{\left|\mathcal{N}_u\right|\left|\mathcal{N}_i\right|}} e_i^{(k)} \\ e_i^{(k+1)}=\sum_{u \in \mathcal{N}_i} \frac{1}{\sqrt{\left|\mathcal{N}_i\right|\left|\mathcal{N}_u\right|}} e_u^{(k)} \end{array}\right. \tag{2} \]

值得注意的是，在LGC中，仅聚合相连的邻居，而不聚合目标节点本身（即自连接）。但是，层组合本质上能获得与自连接相同的效果，因此，在LGC中无需包含自连接。

• 层组合：在 LightGCN 中，唯一可训练的模型参数是第 0 层的嵌入，即所有用户的 \(e_u^{(0)}\) 和所有物品的 \(e_i^{(0)}\) 。给定这些参数，更高层的嵌入可通过公式(2)算出。经过 \(K\) 层 \(L G C\) 后，组合每层获得的嵌入，以形成用户（或物品）的最终表示：

\[e_u=\sum_{k=0}^K \alpha_k e_u^{(k)} ; e_i=\sum_{k=0}^K \alpha_k e_i^{(k)} \tag{3} \]

其中 \(\alpha_k \geq 0\) 表示第 \(k\) 层嵌入的权重，统一设置为 \(\frac{1}{K+1}\) 。

• 模型预测：

  预测分数为用户表示和物品表示的内积：

\[\hat{y}_{u i}=e_u^T e_i \tag{4} \]

矩阵形式

设用户-物品交互矩阵为\(\mathbf{R} \in \mathbb{R}^{M \times N}\) ，其中 \(M\) 和 \(N\) 分别代表用户和物品的数量。若用户\(u\)和物品\(i\)存在交互，则 \(R_{u i}=1\)；反之，若不存在交互，则\(R_{u i}=0\)。

\[\mathbf{A}=\left(\begin{array}{cc} \mathbf{0} & \mathbf{R} \\ \mathbf{R}^T & \mathbf{0} \end{array}\right), \]

设第0层的嵌入矩阵为 \(\mathbf{E}^{(0)} \in \mathbb{R}^{(M+N) \times T}\), 其中 \(T\)是嵌入的维度。因此，LightGCN的矩阵形式为

\[\mathbf{E}^{(k+1)}=\left(\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}\right) \mathbf{E}^{(k)}, \]

其中\(\mathbf{D}\) 是一个 \((M+N) \times(M+N)\) 大小的对角矩阵，对角元素\(D_{i i}\) 表示\(\mathbf{A}\)中第 \(i\)行非零元素的数量。最终，我们得到用于预测的最终嵌入矩阵为

\[\begin{aligned} \mathbf{E} & =\alpha_0 \mathbf{E}^{(0)}+\alpha_1 \mathbf{E}^{(1)}+\alpha_2 \mathbf{E}^{(2)}+\ldots+\alpha_K \mathbf{E}^{(K)} \\ & =\alpha_0 \mathbf{E}^{(0)}+\alpha_1 \ddot{\mathbf{A}} \mathbf{E}^{(0)}+\alpha_2 \tilde{\mathbf{A}}^2 \mathbf{E}^{(0)}+\ldots+\alpha_K \tilde{\mathbf{A}}^K \mathbf{E}^{(0)} \end{aligned} \]

其中 \(\tilde{\mathbf{A}}=\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}\) 是对称归一化矩阵。

综上所述，LightGCN的结构可以用下图表示

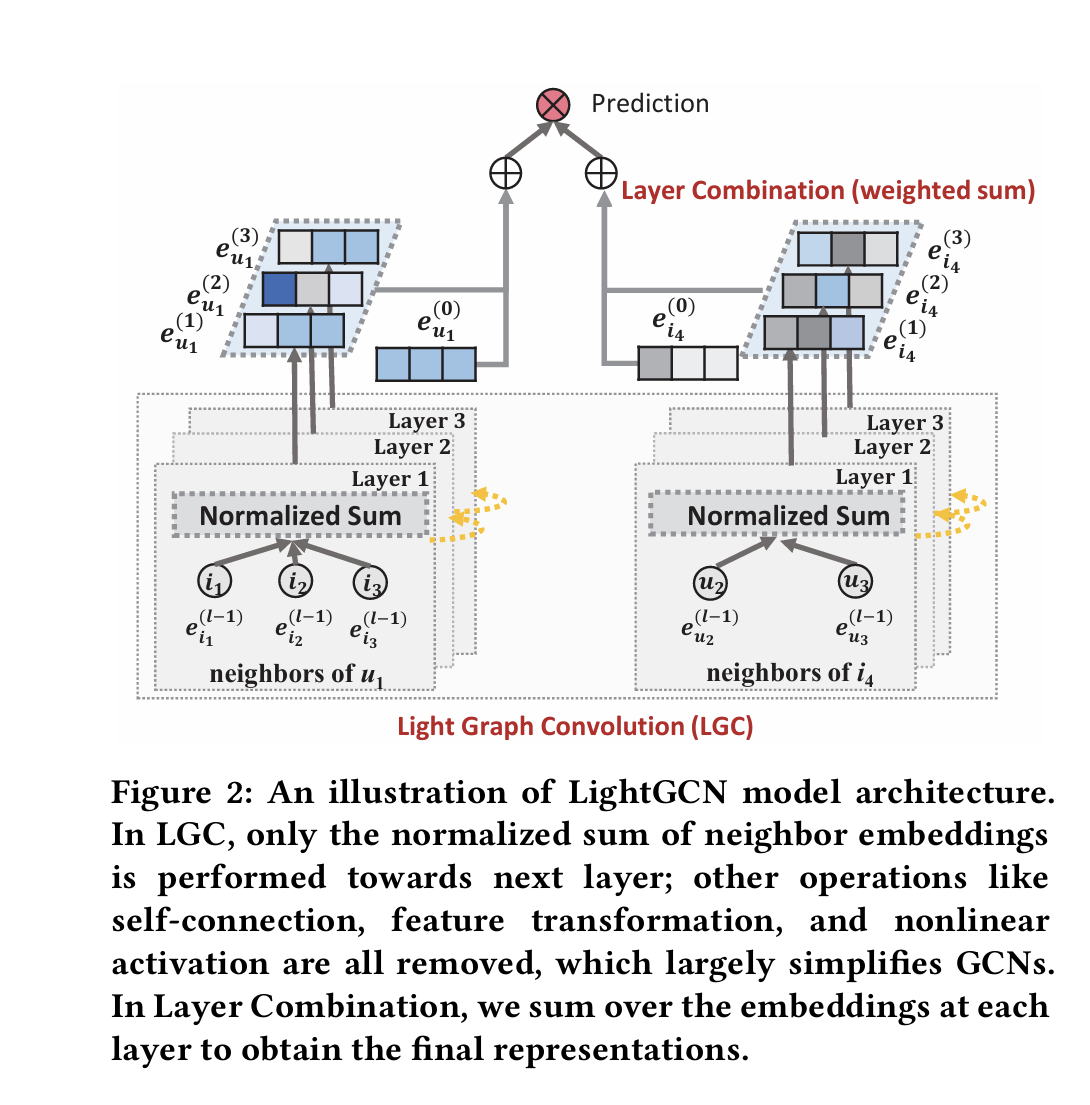
损失函数

LightGCN使用BPR损失：

\[L_{B P R}=-\sum_{u=1}^M \sum_{i \in N_u} \sum_{j \notin N_u} \ln \sigma\left(\hat{y}_{u i}-\hat{y}_{u j}\right)+\lambda\left\|\mathbf{E}^{(0)}\right\|^2 \]

其中\(\lambda\)是超参数。

3. 实验

一些有趣的实验结果：

• 模型表现达到sota。（没达到sota也不会发这篇论文）

• LightGCN比NGCF-fn的表现要好（意料之中，毕竟LightGCN很可能是从NGCF-fn中调出来的）

• 一般来说，使用3层或者4层的LightGCN就可以得到满意的性能，层数更多时，对于模型表现的增益不大。

• 设不使用层组合的LightGCN为LightGCN-single，在Gowalla和Amazon-book两个数据集上做实验，结果如下

  )

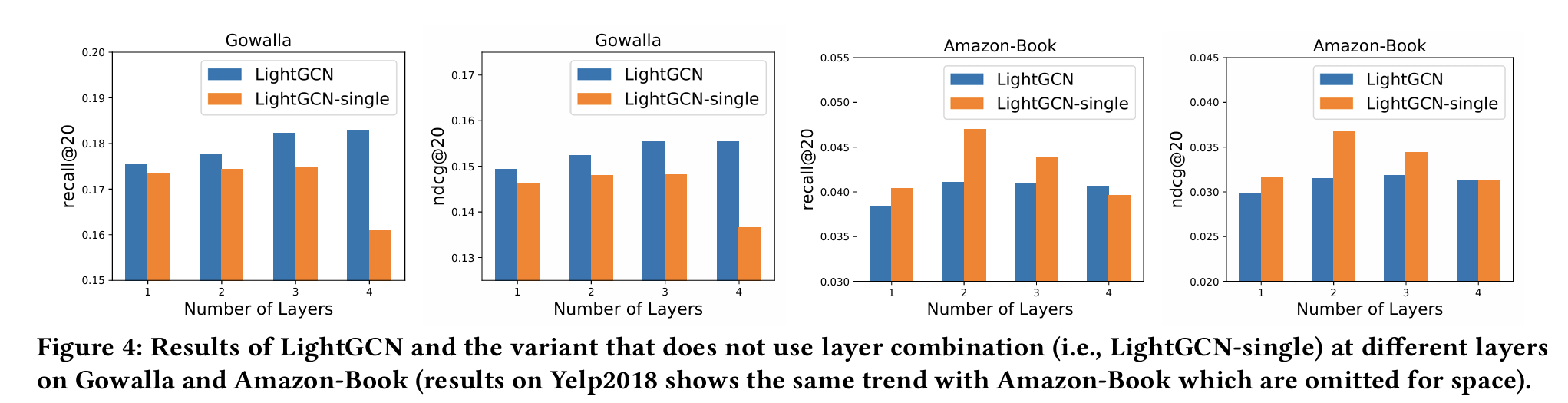  从图中，可以发现：

  1. 对于 LightGCN-single，当层数从 1 增加到 4 时，其性能先提高后下降。多数情况下峰值出现在第 2 层，之后迅速下降到第 4 层的最差点。这表明用一阶和二阶邻居对推荐系统非常有用，但使用高阶邻居时会出现过平滑问题。

  2. 对于 LightGCN，我们发现其性能随层数增加而逐渐提高。即使使用 4 层，LightGCN 的性能也未下降。

  3. 比较两种方法，发现 LightGCN 在 Gowalla 上始终优于 LightGCN-single，但在 Amazon-Book 和 Yelp2018 上并非如此（其中 2 层的 LightGCN-single 表现最佳）。对于这种情况，作者给出的解释是：

     LightGCN-single是LightGCN的特殊情况，当设置 \(\alpha_K\)为 1 ，其他 \(\alpha_k\) 为 \(0\)时，LightGCN就变成了LightGCN-single。因此，通过调整权重\(\alpha_k\)的值，可以实现更好的性能。

• 在LightGCN的卷积操作中，归一化参数采用\(\frac{1}{\sqrt{\left|N_u\right|} \sqrt{\left|N_i\right|}}\)时，模型的表现最好

4. 个人评价

LightGCN的主要idea就来自于对NGCF的消融实验，这给了我们一个启示：在阅读论文的时候，不要被作者看似严谨的推导和实验所吓倒，深度学习模型的表现在很多时候没有任何道理可讲。所以还是要自己复现论文，在模型上做做魔改，说不定你也可以发现一个Light xxx呢。

标签：精读,mathbf,论文,NGCF,right,LightGCN,mathcal,left
From： https://www.cnblogs.com/rh-li/p/18591886