CF2050G Tree Destruction 题解

【题意简述】

你有一棵树，你可以从里面删除一条链上的节点，问剩下的点的联通块数量最大是多少。

【思路】

一眼树形 dp，默认根为 \(1\)。

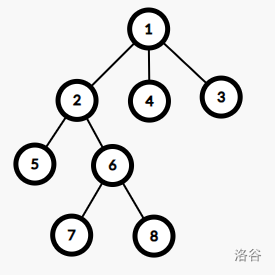
我们以这棵树的 \(1\) 节点作为示例。

设 \(dp[i][0]\) 表示 \(i\) 节点的子树中选一条链，\(i\)​ 不在链上的最大联通块数。

设 \(dp[i][1]\) 表示 \(i\) 节点的子树中选一条链，\(i\) 在链端点的最大联通块数。

设 \(dp[i][2]\) 表示 \(i\) 节点的子树中选一条链，\(i\) 在链中间的最大联通块数。

• \(dp[i][0]\)：\(i\) 不在链上，意味着一定是 \(i\) 的某一个子节点的子树内有一条链。

  • \(dp[son][0]\)：当前儿子也不在链上，如图所示：

    

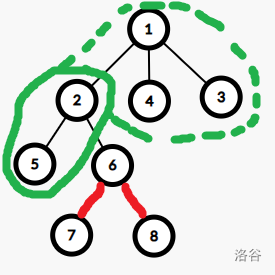
    \(2\) 节点不在红色链上，当前 \(2\) 子树中有一个绿色联通块，发现带上 \(1\) 号点之后联通块扩大，但是个数不变。

  • \(dp[son][1]/dp[son][2]\)：当前儿子在链上，如图所示：

    

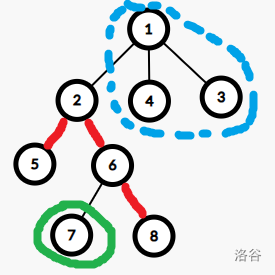
    \(2\) 节点在红色链上，当前 \(2\) 子树中有一个绿色联通块，发现带上 \(1\) 号点之后联通块个数 +1。

• \(dp[i][1]\)：\(i\) 在链的端点，意味着

  • 这个子树内只有这一个点在链上，答案即为子树个数。

  • \(i\) 的子节点有一个处于其子树中链的端点上，如图所示：

    

    \(2\) 节点在红色链上，当前 \(2\) 子树中有两个绿色联通块，连接 \(1\) 号点之后联通块个数 +(子节点个数-1)。

• \(dp[i][1]\)：\(i\) 在链的中间，意味着

  • 有两个子节点处于其子树中链的端点上，如图所示：

    

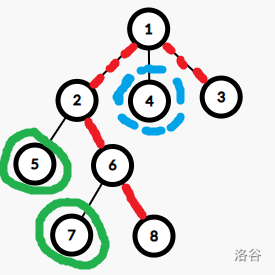
    \(2,3\) 节点在红色链上，当前 \(2\) 子树中有两个绿色联通块，\(3\) 子树中没用联通块，连接 \(1\) 号点之后联通块个数 +(子节点个数-2)。

    选择联通块个数最大的两个子树连起来就好。

然后就很好写了。

【Code】

#include <bits/stdc++.h>
using namespace std;

vector<int>Edge[200005];
int n,u,v,dp[200005][3];

void DFS(int u,int fa){
	int soncnt=0,max0=0,max1=0,sec1=0,max2=0;
	for(auto v:Edge[u]){
		if(v!=fa){
			DFS(v,u),soncnt++;
			max0=max(max0,dp[v][0]);
			max2=max(max2,dp[v][2]);
			if(dp[v][1]>max1){
				sec1=max1;
				max1=dp[v][1];
			}else if(dp[v][1]>sec1){
				sec1=dp[v][1];
			}
		}
	}
	dp[u][0]=max(max0,max(max1,max2)+1);
	dp[u][1]=max(soncnt,max1+(soncnt-1));
	dp[u][2]=max1+sec1+(soncnt-2);
} 

void Main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) dp[i][0]=dp[i][1]=dp[i][2]=0,Edge[i].clear();
	for(int i=1;i<=n-1;i++){
		scanf("%d%d",&u,&v);
		Edge[u].push_back(v);
		Edge[v].push_back(u);
	}
	DFS(1,0);
	printf("%d\n",max({dp[1][0],dp[1][1],dp[1][2]})); 
} 

int T;
int main()
{
	scanf("%d",&T);
	while(T--) Main();
	return 0;
}

【后记】

祝贺我自己，在上蓝前的最后一场 Div.3 AK。

两发罚时全是数组开小，乐。

以后就打不了了。