基于AI、云计算、视频处理与分析、物联网、互联网+等技术,改造现有技术模式和管理手段,实现停车信息资源的全面感知和有效整合、充电基础设施统一规划和统筹利用,实现智慧停车互联互通,全面提升管理效率和服务水平,通过智能化运营提升用户体验。
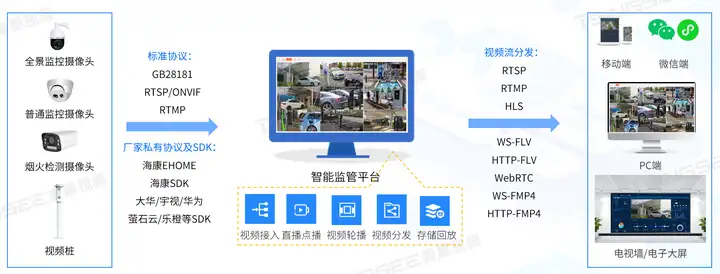
当然智慧充电桩在实际应用中也展现了多项优秀功能,它们不仅提升了充电效率和用户体验,还优化了运营管理。以下是智慧充电桩的一些实际运用功能:
1、智能化、数字化高效运营
通过综合管理平台,可实现远程大规模充电桩的集中化、可视化统一管理,实时掌握终端运行状况,全量记录充电设备、运行状态、车辆进出、视频安全监管等数据信息,通过GPS模块的嵌入,清晰看到每个充电桩的位置坐标,打破运维信息孤岛、响应运营业务的敏捷开发,通过云服务方式能够帮助充电运营商完成数字化运维转型,实现无人值守运营与智能化安全监管,降低充电站/电动车的运营成本,提升用户体验,提高产品及服务的市场竞争力。
2、开放共享
根据场景与用户的需求,支持与其他平台的灵活接通、数据共享、能力集成,获得更多信息来源,适配行业90%以上充电桩通信协议,支持与第三方平台互联互通。
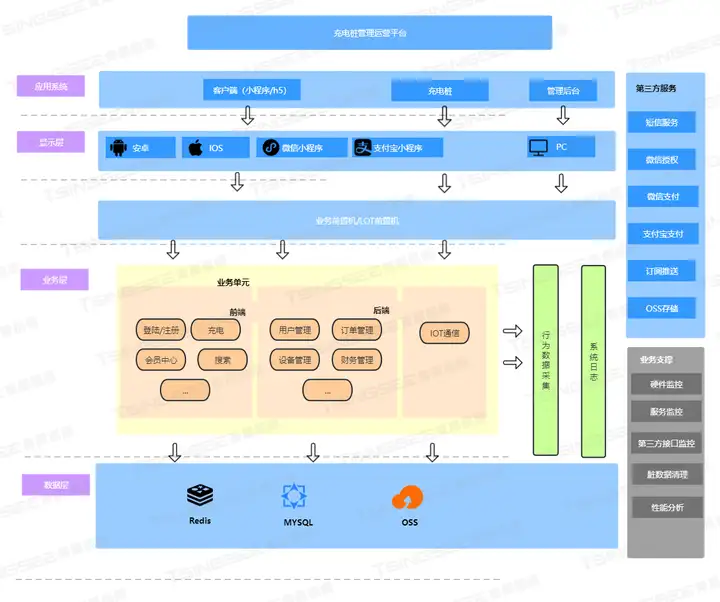
3、支付能力
基于微信、支付宝完善的支付能力,为车主提供无感支付、扫码支付等多种支付方式,为企业提供清分结算、交易管理、账务管理、收支管理等资金管理工具。
4、入口便捷
以微信小程序为服务入口,将充电与停车服务结合,为企业与车主提供更紧密的连接、更便捷的服务、更优质的体验。
5、设备资产监控
提供面向管理的综合分析系统、经营管理系统、车辆监控系统和设备监控系统,为停车管理与运营方提供全方位的实时数据展示与分析服务。
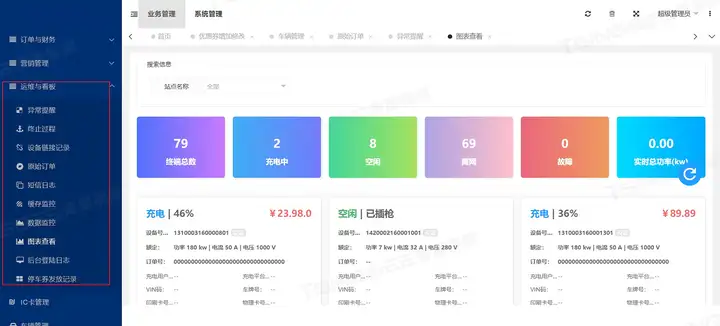
6、支撑海量设备接入和数据高并发处理
支持多网络、多协议、多语言SDK支持,屏蔽物联网碎片化,实现充电设备快速接入,同时可确保设备安全和信息传输安全。
7、支持多协议接入
快速实现多种设备集成、多协议接入、平滑扩展支持海量连接。
新能源汽车智慧充电桩解决方案负责用户端(H5、APP、小程序)、商户端、平台端、硬件端、协议端,在平台和设备之间搭建高效、稳定、通用的应用平台。
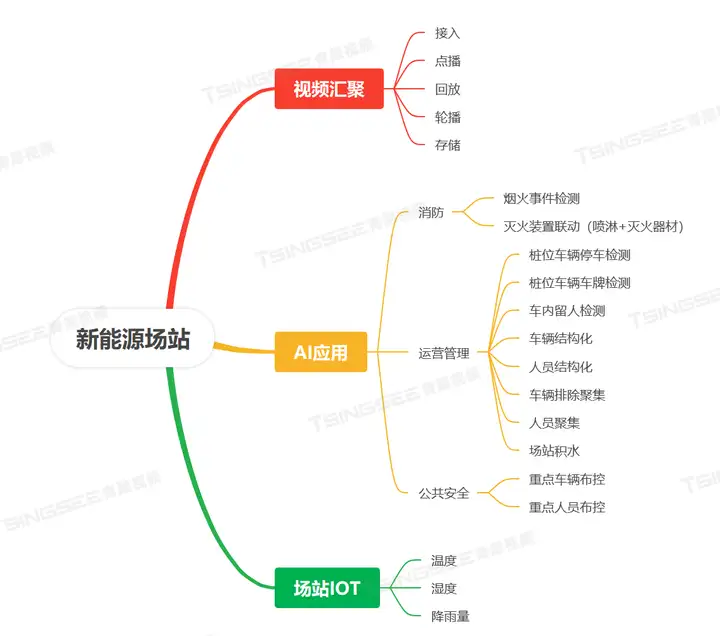
总之智慧充电桩在实际应用中所展现的这些优秀功能,不仅极大地提升了新能源汽车充电的便捷性和安全性,而且通过智能化和自动化的运营管理,优化了能源分配和使用效率。随着技术的不断进步和创新,智慧充电桩将继续扩展其功能,为用户带来更加智能化、个性化的充电解决方案,同时为环境保护和可持续发展做出更大的贡献。
标签:管理,智慧,智能化,运营,充电,领航,设备 From: https://www.cnblogs.com/TSINGSEE/p/18590683