https://www.luogu.com.cn/problem/CF176B

没看懂其他题解为什么说 "可以发现，只要能从一个串变成一个串，都可以通过仅一次变换得到"。

转化

将题目中的操作转化一下：对于一个串 \(s\)，将串 \(s\) 复制一份接到 \(s\) 末尾，然后选择一段长度 \(n \) 的子串。

发现：经过一次操作后，接下来的操作任然是 在原 \(s\) 复制后的串中选择一个长度 \(n\) 的子串。

如图：

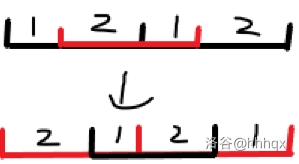
第一个字符串中红色区间表示选择的子串。原 \(s\) 复制后的串，不妨将其分为四段 \(s_1+s_2+s_1+s_2\)。

第一次操作后得到的串 \(t\)，发现其任然可以分为四段 \(s_2+s_1+s_2+s_1\)。

容易看出在 \(t\) 中选择一个长度为 \(n\) 的子串等价于在 \(s\) 中选择一个长度为 \(n\) 的子串。

所以：题目中的 \(a\) 通过多次操作得到的串，这个串通过一步变为 \(b\) 的操作种类数，是固定的，我们不妨直接求出 \(a\) 可以通过几种操作得到 \(b\)，记为 \(cnt\)。

解法

\(cnt\) 可以直接求。

然后考虑 dp。\(f_{i,0/1}\) 表示经过 \(i\) 次操作，当前字符串是 原串 还是 非原串，的操作种类数。

具体转移可以去看其他题解，例如这位大佬的：https://www.luogu.com.cn/article/84ns8qcl 。

Code

#include <bits/stdc++.h>

using namespace std;
using LL = long long;

const LL mod = 1e9 + 7;
const int MAXK = 1e5 + 3;

string a, b;
int k, cnt = 0;
LL f[MAXK][2];

int main(){
	cin >> a >> b >> k;
	if(a == b) cnt++;
	for(int i = 0; i < a.size() - 1; i++){
		string t = a.substr(i + 1, a.size()-i-1) + a.substr(0, i+1);
		if(t == b) cnt++;
	}
	f[0][(a == b ? 0 : 1)] = 1;
	for(int i = 1; i <= k; i++){
		f[i][0] = 1ll * cnt * f[i - 1][1] % mod + 1ll * (cnt - 1) * f[i - 1][0] % mod;
		f[i][0] %= mod;

		f[i][1] = 1ll * (a.size() - cnt) * f[i - 1][0] + 1ll * (a.size() - cnt - 1) * f[i - 1][1] % mod;
		f[i][1] %= mod;
	}
	cout << f[k][0];
	return 0;
}