很多打工人每天的日程安排非常多,很容易会忘记或遗漏。如果能给在电脑桌面上直接使用一款日程提醒软件,就可以准时提醒每项日程事项了,轻松提高办公效率!
下面介绍4款好用的电脑桌面日程体系软件!
一、Win系统自带日历
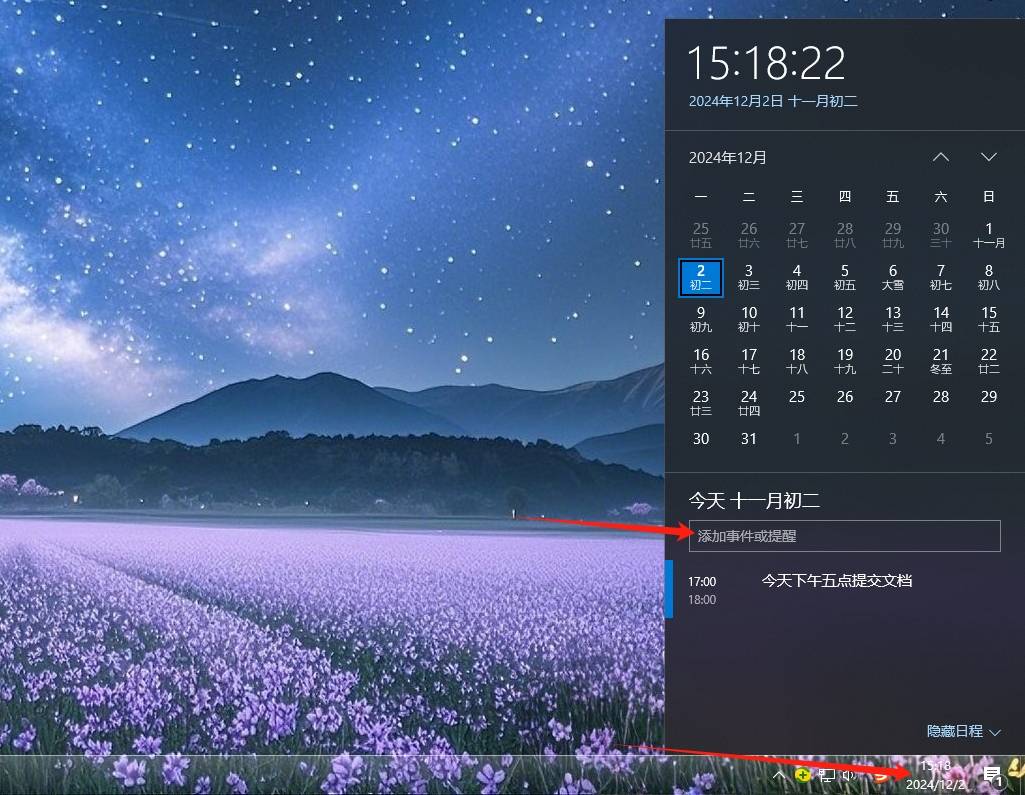
点击电脑桌面右下角的日期,可以在日历中的某个日期下,直接记录日程,并设置提醒时间,到期后可准时收到弹窗、响铃提醒!不过设置重复周期的话,需要点击“更多详细信息”进行设置,操作有点繁琐。
适合在电脑桌面上,设置单次日程提醒的简单需求!
二、敬业签
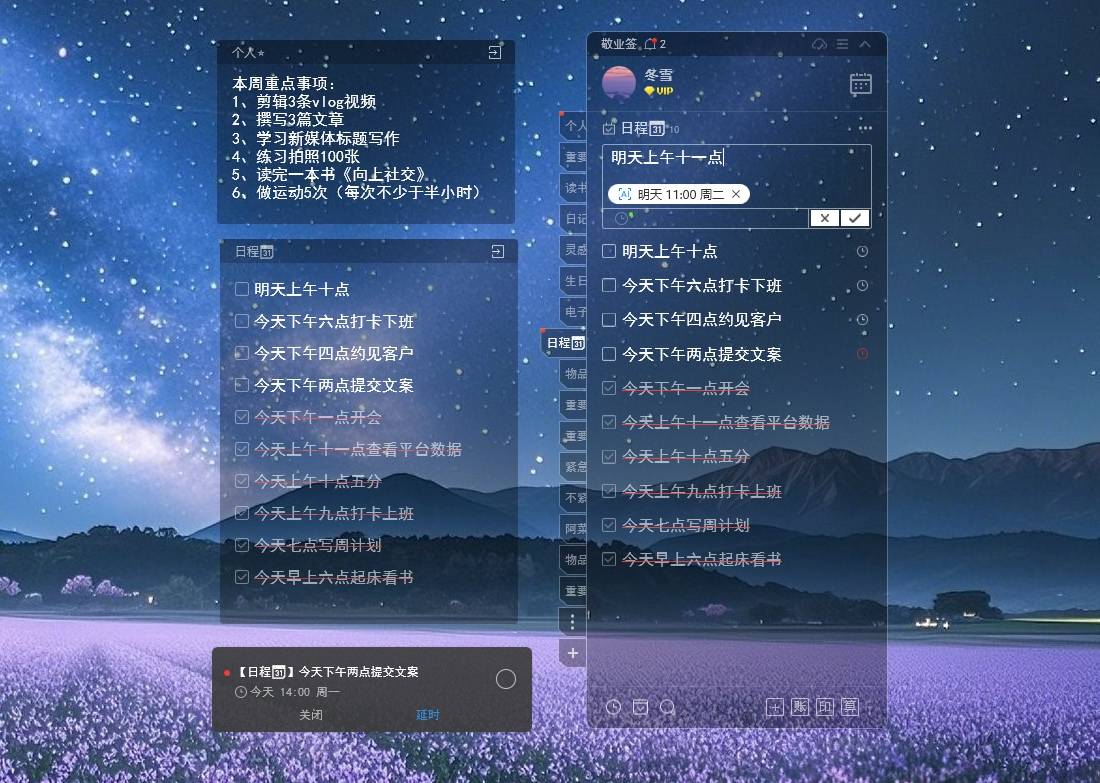
在电脑上打开它,界面自动悬挂在桌面上显示,便签或待办分类中的每条内容,都可以设置提醒时间。文字记录时间点,系统自动设置对应的提醒时间,操作简单;还可以手动设置农历日期以及按天、周、月、年周期重复提醒。
所有提醒日期能以日历月视图形式查看,完成后可一键打勾划掉,所有已完成记录自动归类到完成列表中。
在手机端也可以同步使用它,内容和提醒是多端实时同步的。
适合在电脑、手机上同步做笔记、便签记事、管理日程提醒的人!
三、Trello
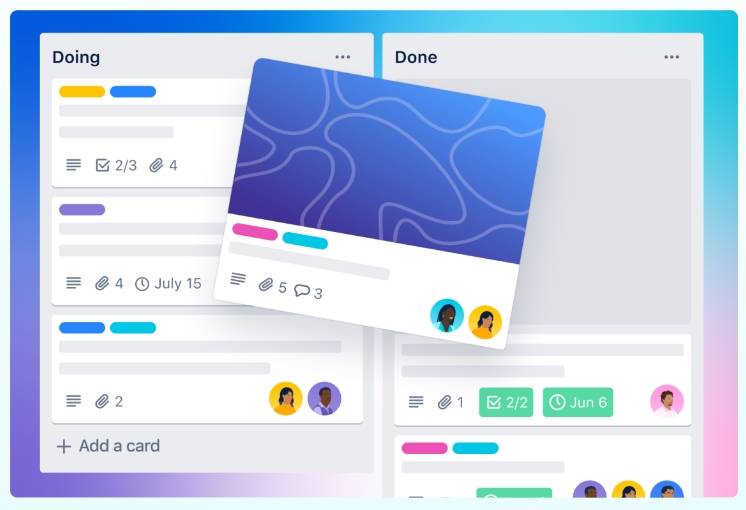
基于Web的可视化项目管理工具,旨在提供一种灵活、易于理解和使用的任务管理系统。它通过看板、列表和卡片的形式,将复杂的项目管理流程简化为直观的管理工具,使团队成员能够轻松看到整个项目的状态,并了解自己的责任和任务。
适合团队、个人、家庭的项目任务管理。
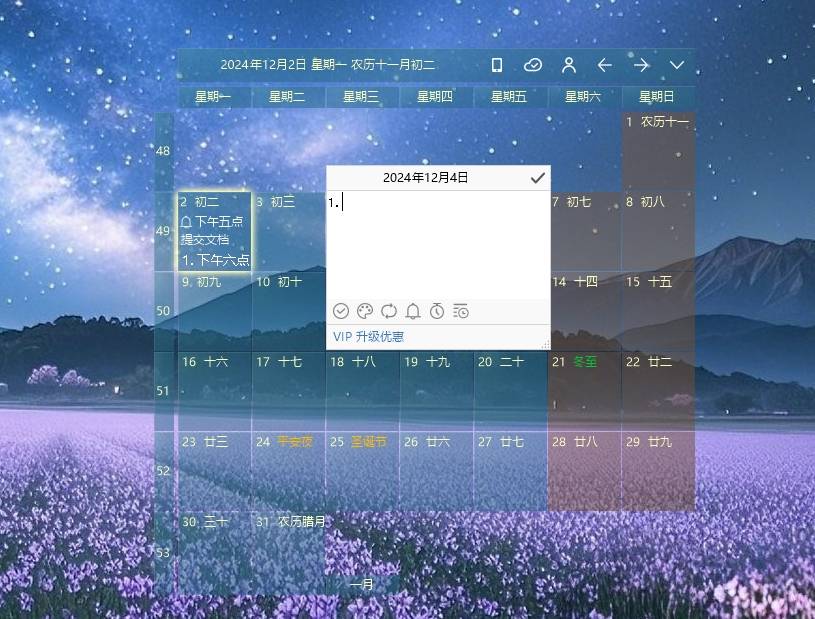
四、日历清单
以日历的形式固定在电脑桌面上显示,可以直接在某个日期下添加日程,设置提醒时间。可在电脑、手机等多端设备同步使用!
但是想要标记完成某条日程,需要在日程详情中勾选,而不能一键打勾标记完成,这点不太方便。
适合只记录日程、设置提醒的用户,如果需要同时记录详细的事项,笔记,它无法实现!