链式二叉树

标签：遍历 que 二叉树 链式 NULL root 节点

引言

在探讨数据结构时，我们不难发现，虽然普通的链式二叉树在存储数据上可能不如前面用数组模拟二叉树直观，但其独特的结构为后续的复杂数据结构奠定了基础。特别是当我们谈及搜索问题时，搜索二叉树以其高效的搜索性能脱颖而出，与二分查找法有着异曲同工之妙。但是，二分查找法在实际应用中受限颇多，它要求数据必须有序且存储在数组中，这一条件往往难以满足。更何况，数组在增删元素时，需要移动大量数据，效率较低。

但是，搜索二叉树虽然也面临一些挑战，如不平衡时可能导致搜索效率下降，但其灵活的节点插入和删除操作，以及基于节点值自动排序的特性，使其在许多应用场景中仍然具有显著优势。为了进一步优化搜索性能，我们引入了平衡二叉树、哈希表、B树等高级数据结构。特别是B树，作为数据库系统的底层核心之一，其高效的多路搜索特性极大地提升了数据处理的效率。

其实，在实际应用中，由于普通二叉树在数据存储和检索方面存在局限性，我们并不常直接用它来存储数据。但是，在学习数据结构的道路上，普通二叉树扮演着举足轻重的角色。我们之所以要深入研究它，主要有两大原因：首先，它为后续学习更复杂的树形数据结构奠定了坚实的基础；其次，在各类考试中，普通二叉树往往是不可或缺的考点。

因此，我们将把重点放在对普通二叉树结构的理解上，而不是过多地纠结于其增删查改的具体操作。这是因为，掌握二叉树的结构特点，对于我们后续学习其遍历算法，以及理解更复杂的树形数据结构具有至关重要的意义。

在学习链式二叉树之前，我们需要这样去看待一棵二叉树：一棵二叉树或者就是由根和它的左子树和右子树组成；而单独看它的左子树和右子树，又是由根和对应的左子树和右子树组成。

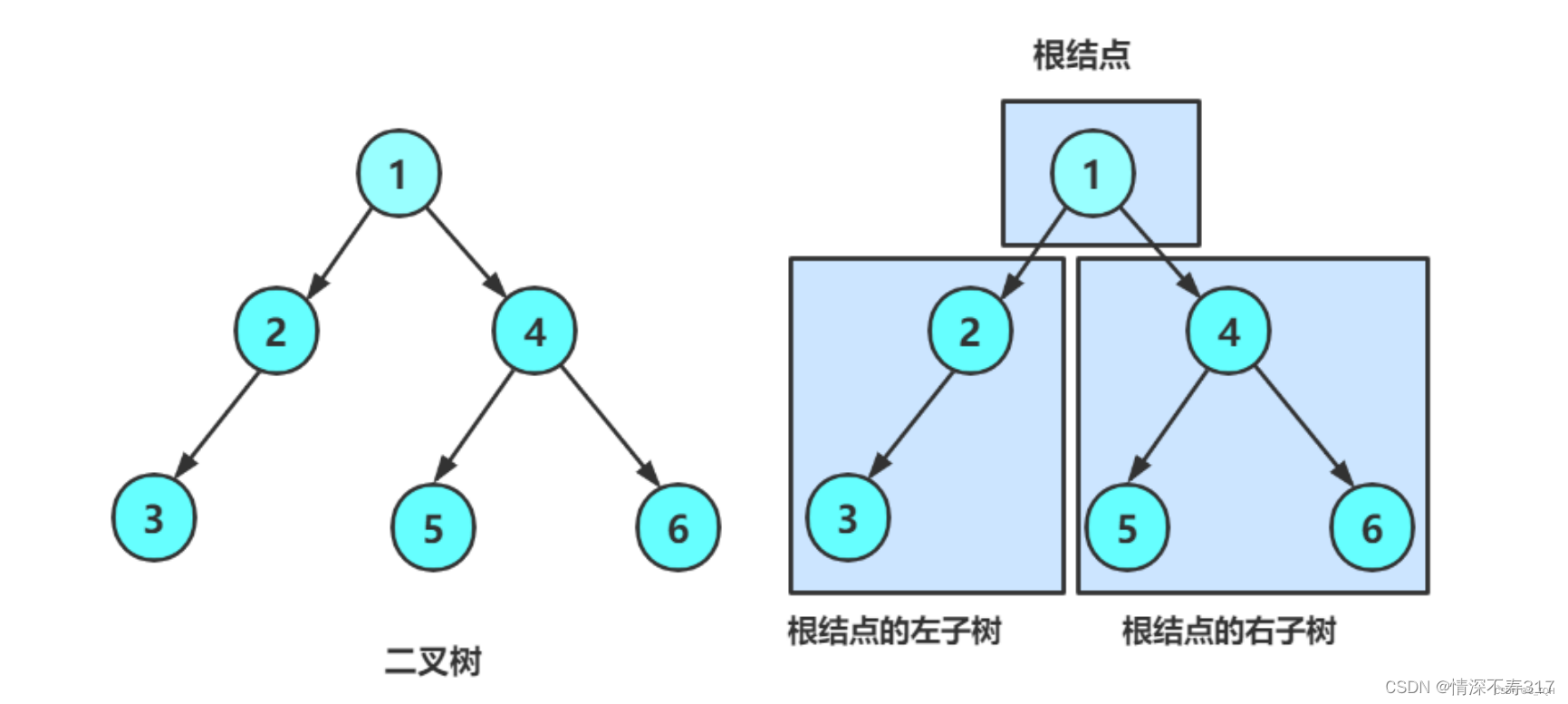
 例如上图中的树，1是根，它的左子树由2和3组成，右子树由4、5、6组成；在它的左子树中，树根是2，左子树由3组成，右子树为空；在它的右子树中，树根是4，左子树由5组成，右子树由6组成。

创建链式二叉树（含代码）

数据结构

typedef char dataType;
typedef struct BinaryTreeNode {
	dataType data;
	struct BinaryTreeNode* left;//左孩子
	struct BinaryTreeNode* right;//右孩子
}BTNode;

创建节点

BTNode* createBTNode(dataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	node->data = x;
	node->left = node->right = NULL;
	return node;
}

生成树（测试案例）

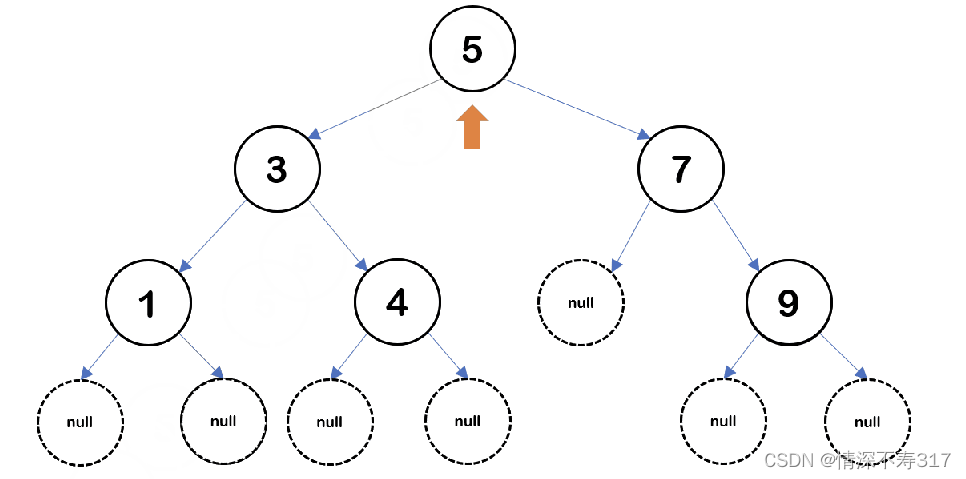
BTNode* createBinaryTree()
{
	BTNode* node0 = createBTNode(5);
	BTNode* node1 = createBTNode(3);
	BTNode* node2 = createBTNode(7);
	BTNode* node3 = createBTNode(1);
	BTNode* node4 = createBTNode(4);
	BTNode* node5 = createBTNode(9);

	node0->left = node1;
	node0->right = node2;
	node1->left = node3;
	node1->right = node4;
	node2->right = node5;

	return node0;
}

遍历二叉树

二叉树的遍历分前序遍历、中序遍历、后序遍历和层次遍历。

二叉树的前中后序遍历常用递归实现，因为递归能自然地匹配二叉树的递归结构。递归的好处包括代码简洁、逻辑清晰，以及易于理解和维护。

在写实现他们的代码之前，我们需要知道他们对应的遍历顺序和规则，还要能根据给出的链式二叉树图片能写出它对应的遍历。

层次遍历，顾名思义，就是按照每层去遍历，后面我们会详细讲解。

前序遍历

遍历顺序

根→左子树→右子树

测试案例中的树的前序遍历顺序：5→3→1→NULL（1的左孩子）→NULL（1的右孩子）→4→NULL（4的左孩子）→NULL（4的右孩子）→7→NULL（7的左孩子）→9→NULL（9的左孩子）→NULL（9的右孩子）

代码

void preOrder(BTNode* root)
{
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	preOrder(root->left);
	preOrder(root->right);
}

递归展开图

 

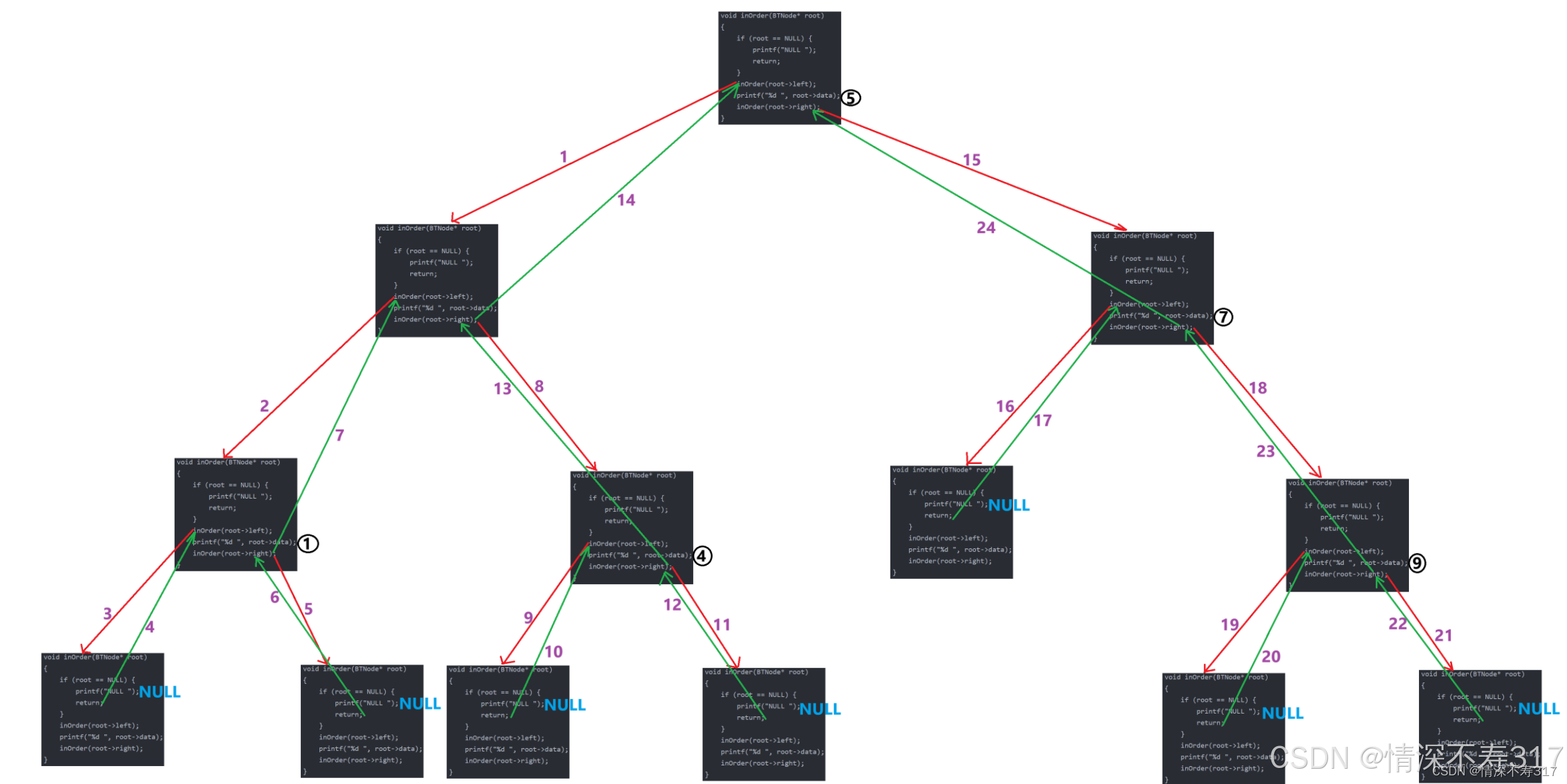
中序遍历

遍历顺序

左子树→根→右子树

测试案例中的中序遍历顺序：NULL（1的左孩子）→1→NULL（1的右孩子）→3→NULL（4的左孩子）→4→NULL（4的右孩子）→5→NULL（7的左孩子）→7→NULL（9的左孩子）→9→NULL（9的右孩子）

代码

void inOrder(BTNode* root)
{
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	inOrder(root->left);
	printf("%d ", root->data);
	inOrder(root->right);
}

递归展开图

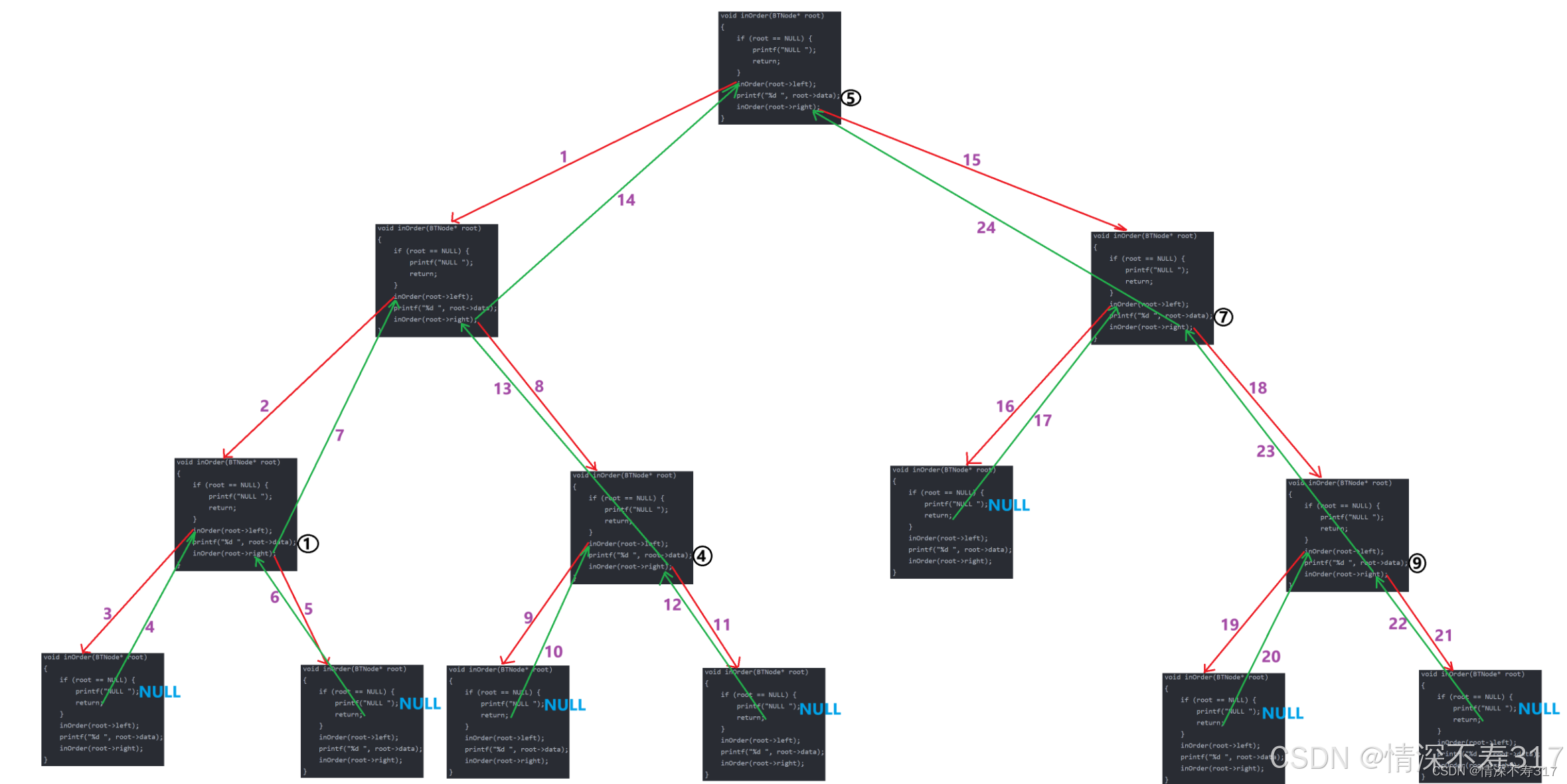
后序遍历

遍历顺序

左子树→右子树→根

测试案例中的后序遍历顺序：NULL（1的左孩子）→NULL（1的右孩子）→1→NULL（4的左孩子）→NULL（4的右孩子）→4→3→NULL （7的左孩子）→NULL（9的左孩子）→NULL（9的右孩子）→9→7→5

代码

void postOrder(BTNode* root)
{
	if (root == NULL) {
		printf("NULL ");
		return;
	}
	postOrder(root->left);
	postOrder(root->right);
	printf("%d ", root->data);
}

（这里就不放递归展开图了）

层次遍历

思路

层序遍历也称为广度优先遍历，我们需要借助队列来实现它。我们先通过一张图来理解它的实现：

 

具体步骤如下：

1. 检查根节点：首先确保树的根节点不为空。如果为空，则无法进行层序遍历。

2. 初始化队列：创建一个空的队列，用于存储将要访问的节点。

3. 加入根节点：将根节点加入队列中。这是遍历的起点。

4. 遍历队列：开始一个循环，条件是队列不为空。这个循环会一直进行，直到队列中的所有节点都被访问过。

   • 访问节点：将队首元素取出，访问（通常是打印）该节点的数据。

   • 加入子节点：检查当前节点的左子节点和右子节点是否存在。如果存在，将它们依次加入队列的末尾。这样，下一轮循环时会访问这些子节点，从而实现了按层访问。

5. 队列清理：当队列为空，即所有节点都被访问过后，结束循环。此时，层序遍历完成。最后，销毁队列。

代码

这里的队列实现，我们用前面文章中队列的代码：

 

但是注意，入队的元素是二叉树的节点的指针，随意头文件部分需要稍加修改：

typedef struct BinaryTreeNode* QdataType;

void levelOrder(BTNode* root)
{
	assert(root);
	Queue que;
	initQueue(&que);
	pushQueue(&que, root);

	while (!emptyQueue(&que))
	{
		BTNode* front = queueFront(&que);
		popQueue(&que);
		printf("%d ", front->data);
		if(front->left)
			pushQueue(&que, front->left);
		if (front->right)
			pushQueue(&que, front->right);
	}
	queueDestroy(&que);
}

判断一棵树是不是完全二叉树

分析

 

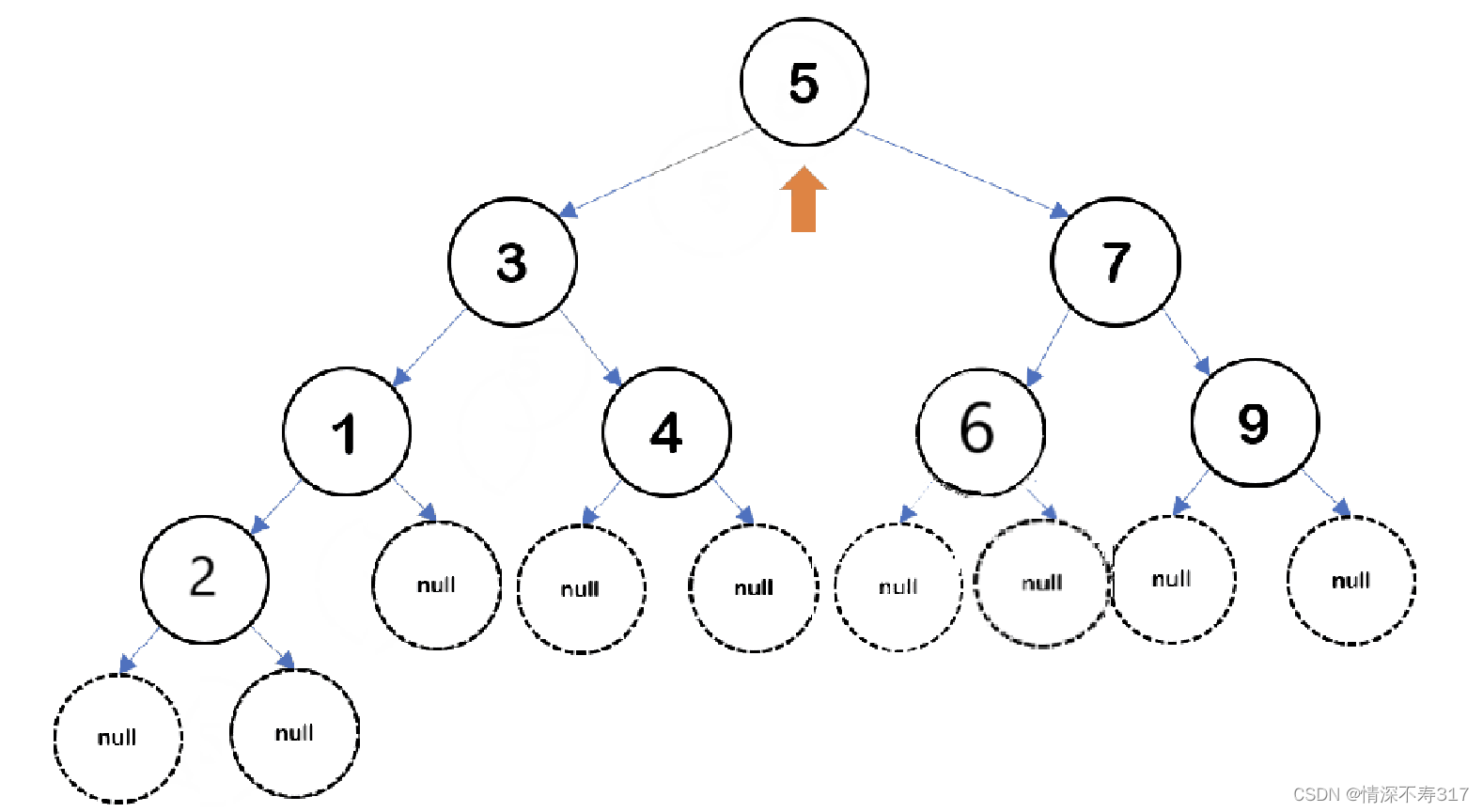
 我们以这棵完全二叉树为例:

我们可以从图片看出，这棵树是一颗完全二叉树。如果按层序去遍历它（包括空节点也遍历上），我们会发现它的遍历顺序如下：

 

 

 我们再来看看这颗非完全二叉树：

如果按层序去遍历它（包括空节点也遍历上），我们会发现它的遍历顺序如下：

 我们发现，完全二叉树一旦遍历到了空节点，后面一直都会是空节点；而非完全二叉树一旦遍历到了空节点，后面不会一直都是遍历的空节点。

思路

所以，要想判断一棵树是不是完全二叉树，我们只用按层序遍历让里面的节点入队，叶子节点的空节点也要入队上。我们每次遍历其实是访问队头元素，一旦当前访问的队头元素是空节点，我们就判断一下队列中剩下的元素有没有非空节点，有的话说明不是完全二叉树，没有的话说明就是完全二叉树。

代码

bool isCompleteBinaryTree(BTNode* root)
{
	assert(root);
	Queue que;
	initQueue(&que);
	pushQueue(&que, root);

	while (!emptyQueue(&que))
	{
		BTNode* front = queueFront(&que);
		popQueue(&que);
		if (front)
		{
			pushQueue(&que, front->left);
			pushQueue(&que, front->right);
		}
		if (front == NULL) {
			break;//当前访问的队头元素是空节点就退出
		}
	}
	while (!emptyQueue(&que)) //判断一下队列中剩下的元素有没有非空节点
    {
		BTNode* front = queueFront(&que);
		popQueue(&que);
		if (front) {
			queueDestroy(&que);
			return false;
		}
	}
	queueDestroy(&que);
	return true;
}

销毁二叉树

分析

销毁二叉树，其实也是一种遍历的过程，每遍历到一个节点就去释放它。我们前面讲过前中后序遍历和层序遍历，那用哪个比较好呢？

当然是后序遍历。

为什么呢？我们一起来看一下：

如果采用先序遍历、中序遍历或层序遍历来销毁二叉树，可能会在销毁根节点后无法再访问其左右子树，导致子树无法被正确销毁。而后序遍历则可以确保在销毁根节点之前，其左右子树都已经被完整销毁。

代码

void destroyBinaryTree(BTNode* root)
{
	if (root == NULL) {
		return;
	}
	destroyBinaryTree(root->left);
	destroyBinaryTree(root->right);
	free(root);
	root = NULL;
}

关于DFS和BFS

DFS就是深度优先搜索，BFS就是广度优先搜索。

不能将广度优先搜索和层序遍历、深度优先搜索和前序遍历混为一谈。二叉树的层序遍历只是在二叉树中的广度优先搜索，而前序遍历只是在二叉树中的深度优先搜索。

标签：遍历,que,二叉树,链式,NULL,root,节点
From： https://blog.csdn.net/2403_82706967/article/details/144126100